水文站流量測驗代表垂線分析原理及應用

劉煒　王懷柏　段雯　胡躍斌　李蘭濤

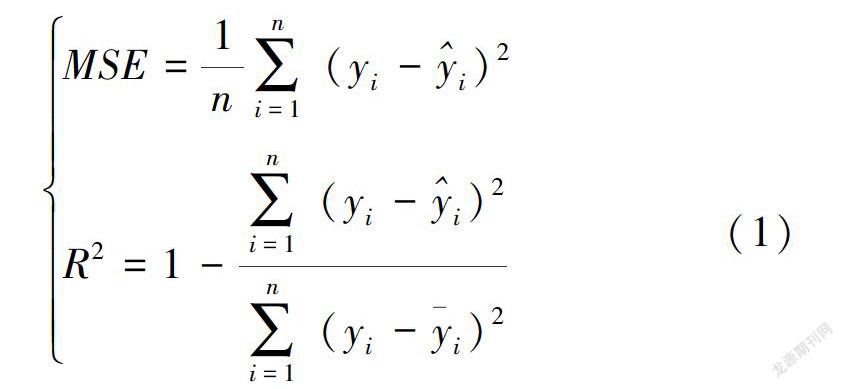
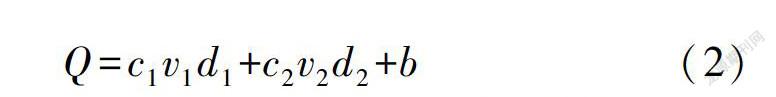
摘要：以龍門水文站基上155斷面為例，選取該斷面1974-2012年約640個實測斷面流量測次作為分析數據集，起點距每隔2m選取一條垂線，對垂線水深和斷面平均水深進行線性回歸，并計算決定系數和均方誤差，用決定系數作為評價指標，優選出最佳代表垂線位置。結果表明：若在龍門站基上155斷面起點距分別為54、188 m處設置固定垂線實測流速和水深，使用回歸公式來計算流量，則可以達到標準差229 m3/s、相對標準差5%的估算精度。

關鍵詞：線性回歸;代表垂線;流量測驗;龍門水文站

中圖分類號：TV856;TV882.1

文獻標志碼：A

doi：10.3969/j .issn.1000- 1379.2019.04.002

水文站在常規流量測驗中，常通過施測均勻布設在測流斷面上各條垂線的水深和流速來計算流量。通過代表垂線分析，可以建立少量垂線實測要素與全斷面測量結果的回歸關系，在實際測驗中只在這些垂線位置進行要素采樣，從而達到降低工作強度、提高測驗效率的目的。此外，若選取的代表垂線[1]能避開流速較大的中泓范圍，則可在一定程度上降低高洪測驗作業的危險性。

1 代表垂線分析的基本原理

代表垂線分析[2]的目標是尋找少量垂線，使得在這些垂線處某個水文要素的實測值可以代表該要素的全斷面綜合值。代表垂線分析包括回歸分析和垂線優選兩部分。回歸分析[3-4]是指對給定的垂線位置，以目標要素的垂線觀測值為自變量、全斷面綜合值為因變量建立回歸關系：垂線優選是指對不同垂線的回歸結果進行評價比較，選出符合一定精度指標的代表垂線位置。

流量測驗所涉及的目標要素包括水深、流速、流量等3項。根據對問題性質的推斷，本文采用線性回歸算法（一元或多元）[5]建立模型，通過窮舉法優選垂線位置。回歸模型的構成見表1。

回歸結果評價采用均方誤差（MSE）和決定系數（R2）兩個指標。它們的計算公式分別為式中：n為樣本數量;Yi為實測值;Yi為預測值;Yi為實測值均值。

2 實例分析結果

2.1 水深代表單垂線

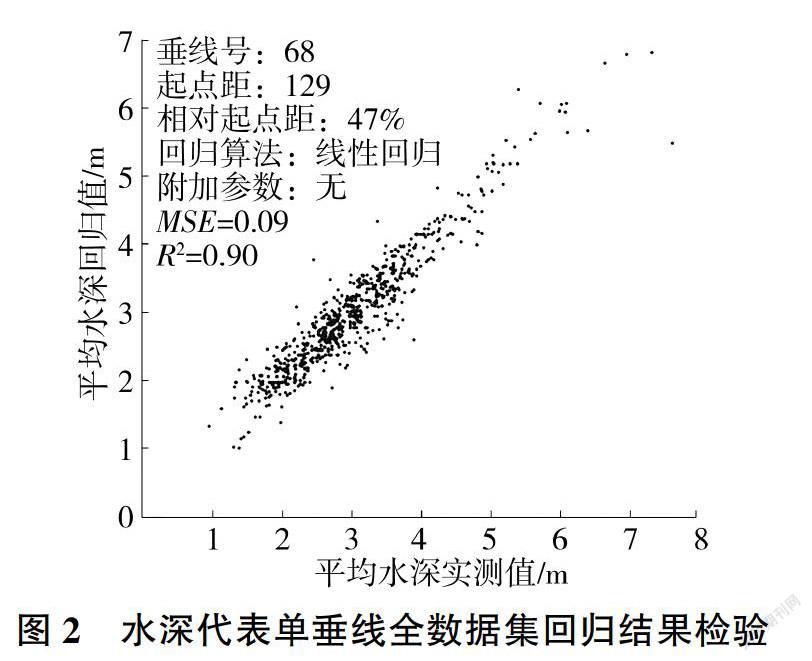
水深代表單垂線法是指使用一條垂線的實測水深來回歸計算斷面平均水深。以龍門水文站基上155斷面為例，具體步驟為：選取該斷面1974-2012年約640個實測斷面流量測次作為分析數據集，起點距每隔2m選取一條垂線，對垂線水深和斷面平均水深進行線性回歸，并計算R2和MSE。用R2作為評價指標，優選出最佳起點距垂線位置。

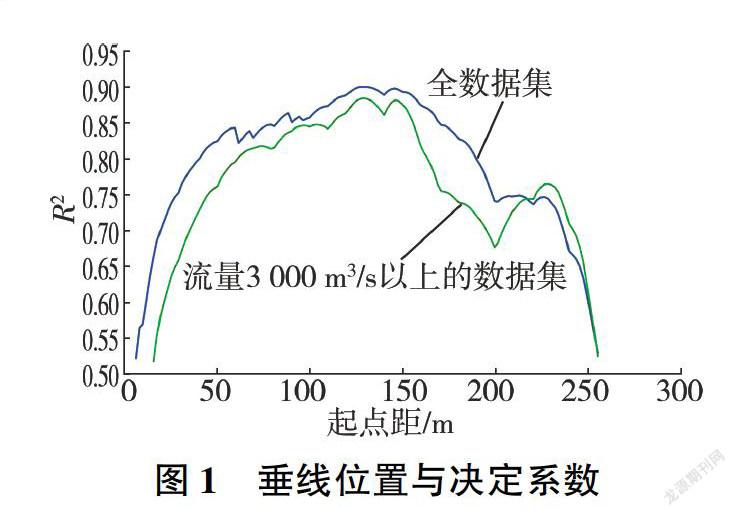
不同流量級的最優代表垂線位置不同，代表性也有差異。本文按全數據集和流量3 000 m/s以上的數據集分別進行計算。垂線起點距及相應的R2見圖1。最優水深代表垂線大致在斷面中間位置，若以決定系數大于0.85為標準，則代表垂線的可選起點距區間為（113，155）。全數據集最優代表垂線的回歸結果檢驗見圖2。

2.2 水深代表雙垂線

水深代表雙垂線是指使用兩條垂線實測水深來回歸計算斷面平均水深。其優選方法與單垂線類似，也是尋找具有最優代表性的垂線位置。兩者區別在于，雙垂線是在由兩個垂線起點距構成的二維空間里進行計算和優選。

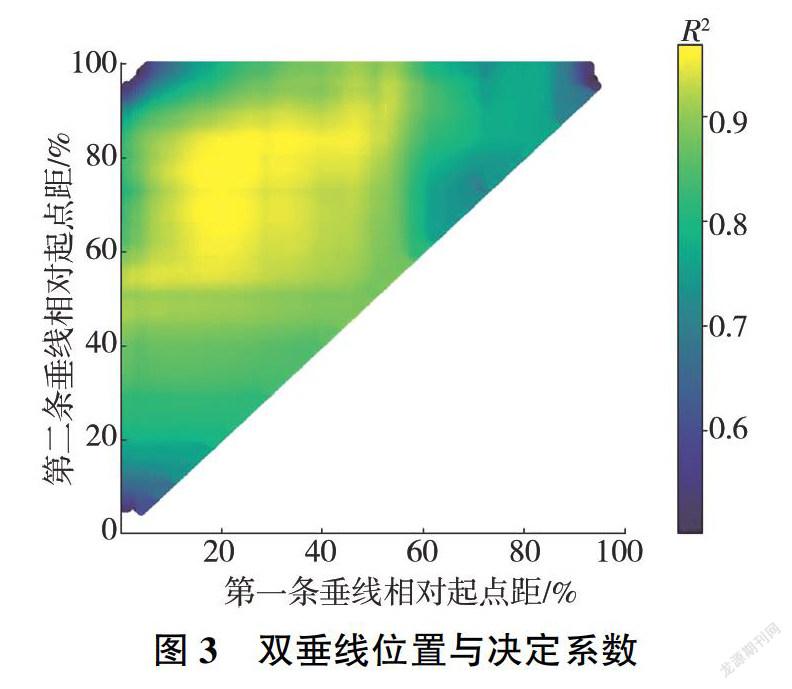
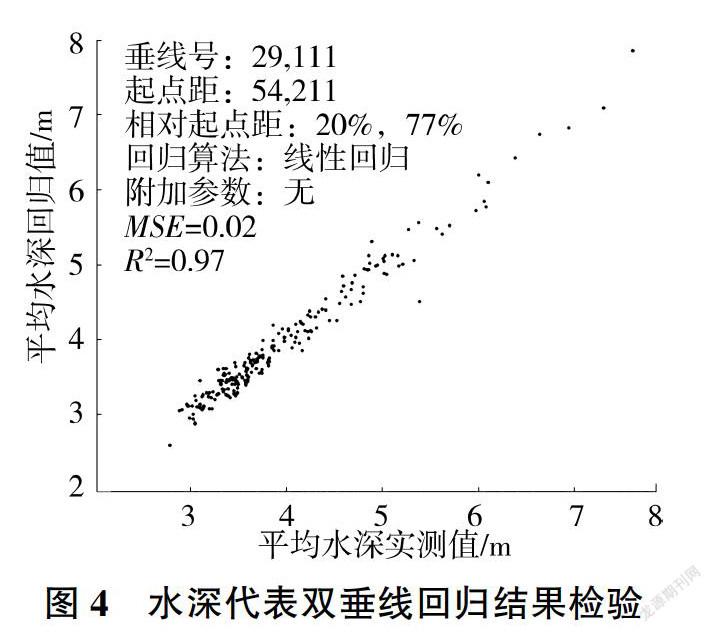
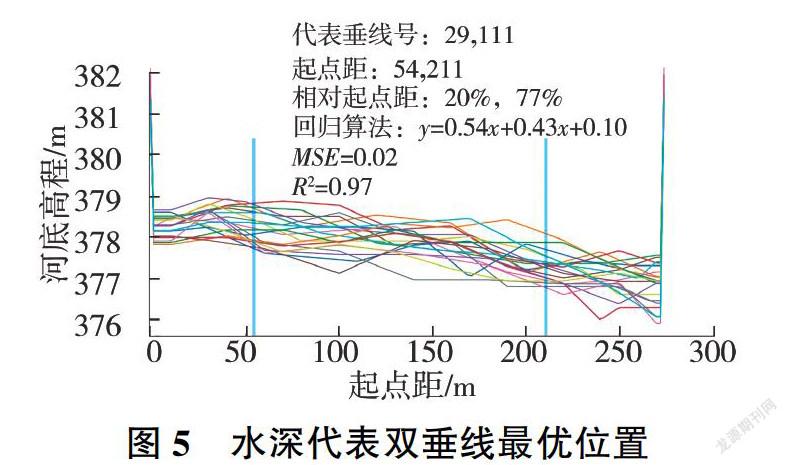
在具體算法中，采用窮舉策略對所有有效垂線位置組合（按2m起點距步長，共10 129對組合）進行回歸分析和指標計算，R2分析結果見圖3，圖中橫.縱坐標分別為第一、第二條垂線的相對起點距（相對于全斷面寬的百分比）。由圖3可知，R2的最大值出現在空間偏左上位置，對應的兩條垂線（相對起點距分別為20%、77%）即為最優水深代表雙垂線，其回歸結果檢驗及位置示意見圖4、圖5（圖5中不同顏色的線條表示不同測次的河底形態）。

2.3 流速代表雙垂線

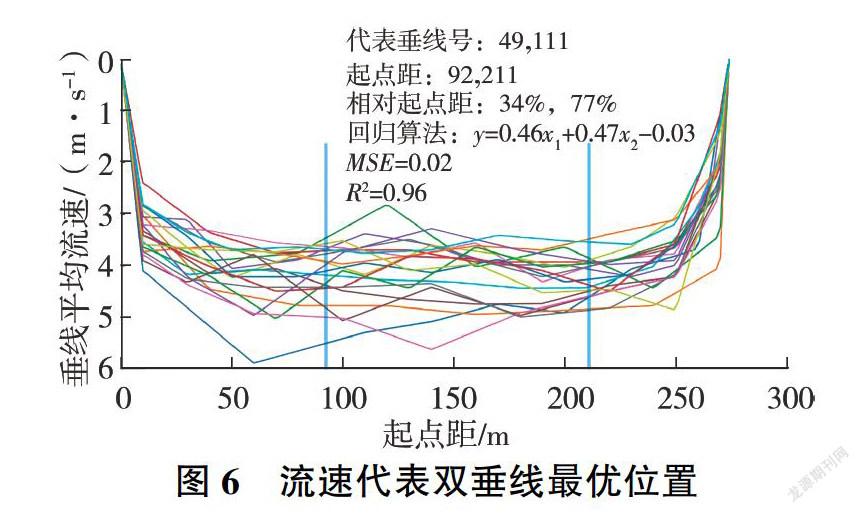
采用類似的方法也可以得到流速代表垂線。用一條或兩條垂線的實測流速代人回歸方程，得到斷面平均流速。經分析，最優流速代表雙垂線的R2為0.96，MSE為0.02，其位置見圖6。

2.4 流量代表雙垂線

流量代表雙垂線是指用兩個起點距位置的水深和垂線流速來回歸斷面流量。流量代表垂線法更符合生產實際需要，依據流量的構成原理，設計回歸公式形式為

Q=C1vld1+C2V2d2+b

（2）式中：Q為計算流量;v1、d1分別為第一條垂線的流速和水深;v2、d2分別為第二條垂線的流速和水深;c1、C2為回歸系數。

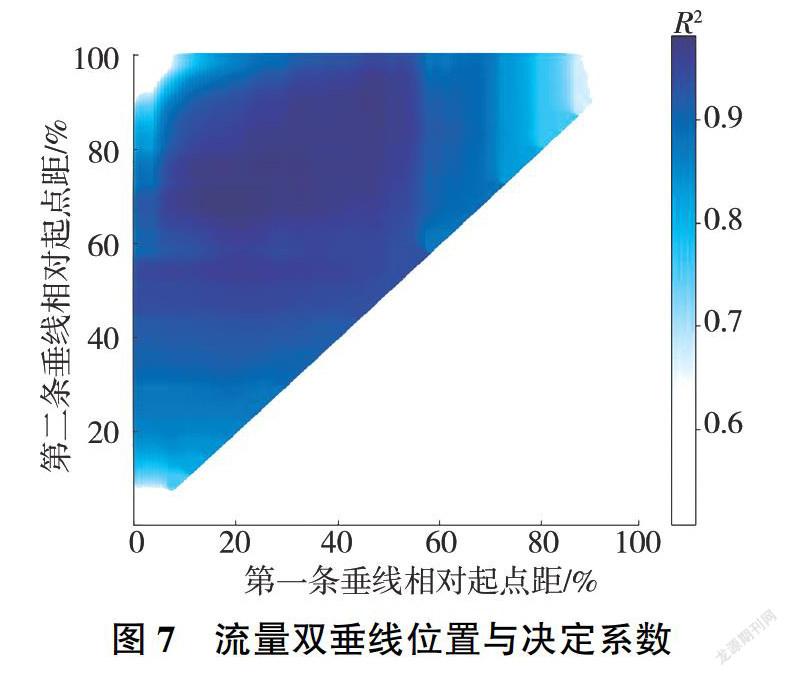
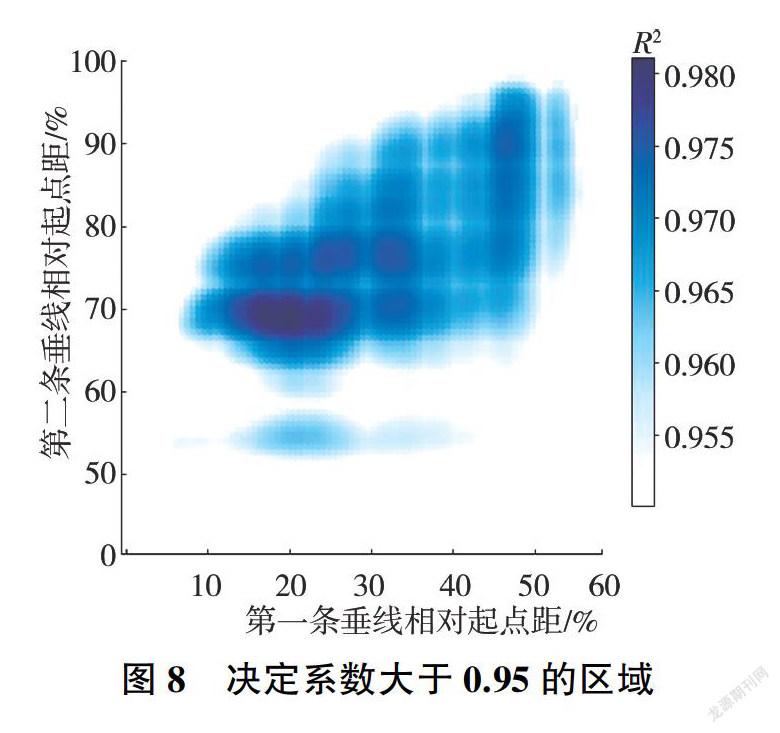
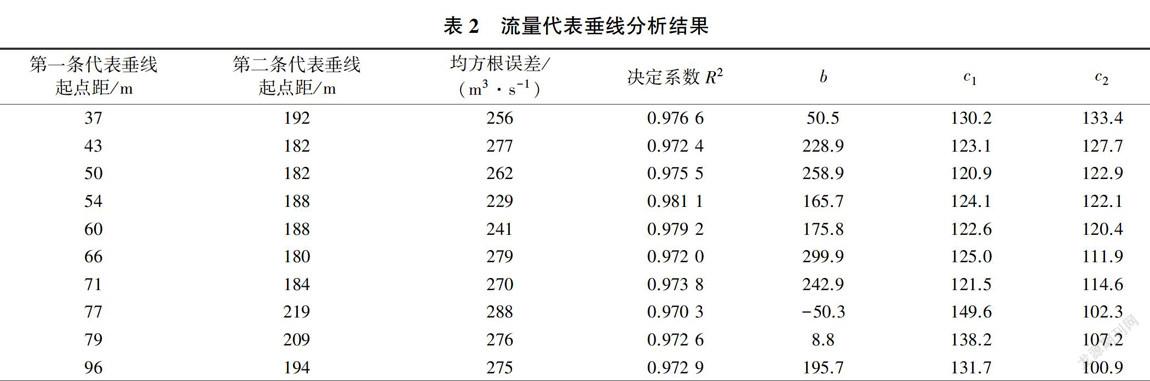
龍門水文站基上155斷面的R2分析結果分別見圖7、圖8。圖7為全空間的遍歷搜索結果，圖8為將R2大于0.95的區域放大并重新渲染的結果。圖8表明，存在一定的垂線選擇范圍，在此范圍內的代表雙垂線均具有足夠的代表性。隨機抽取R2大于0.97的10對起點距位置（包含最優解），回歸分析結果見表2。

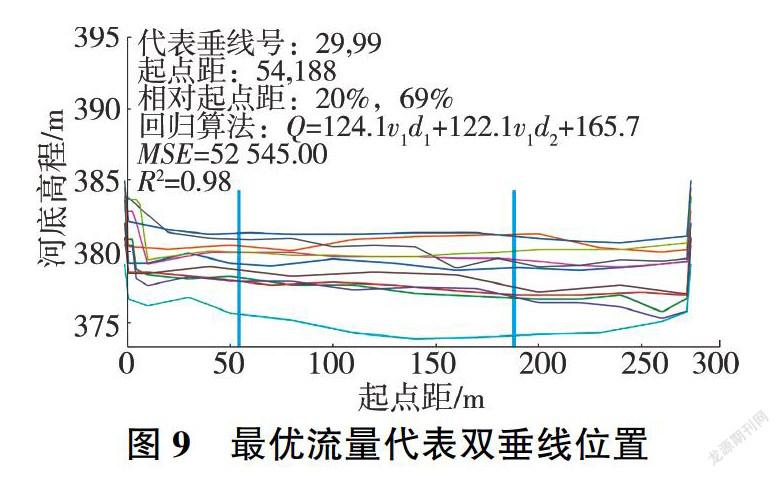
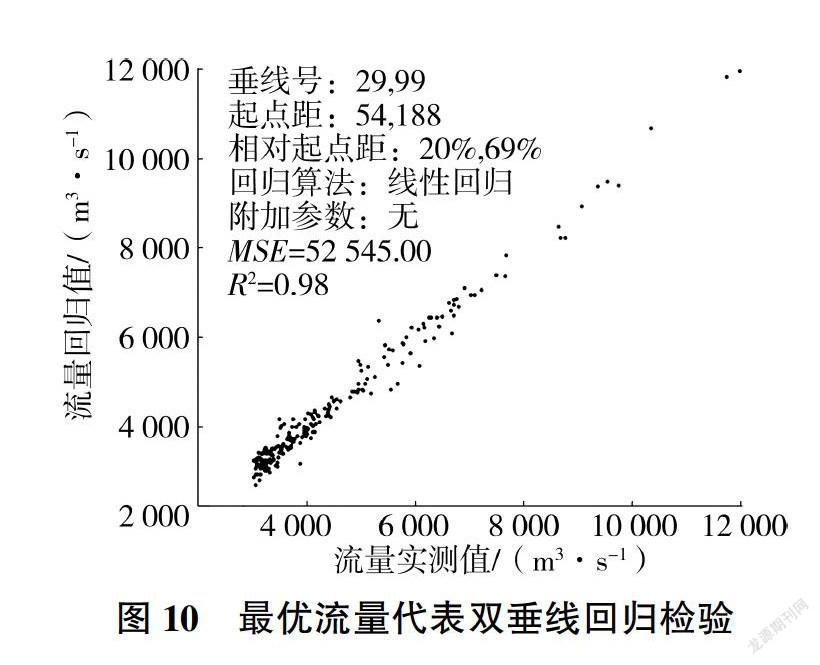
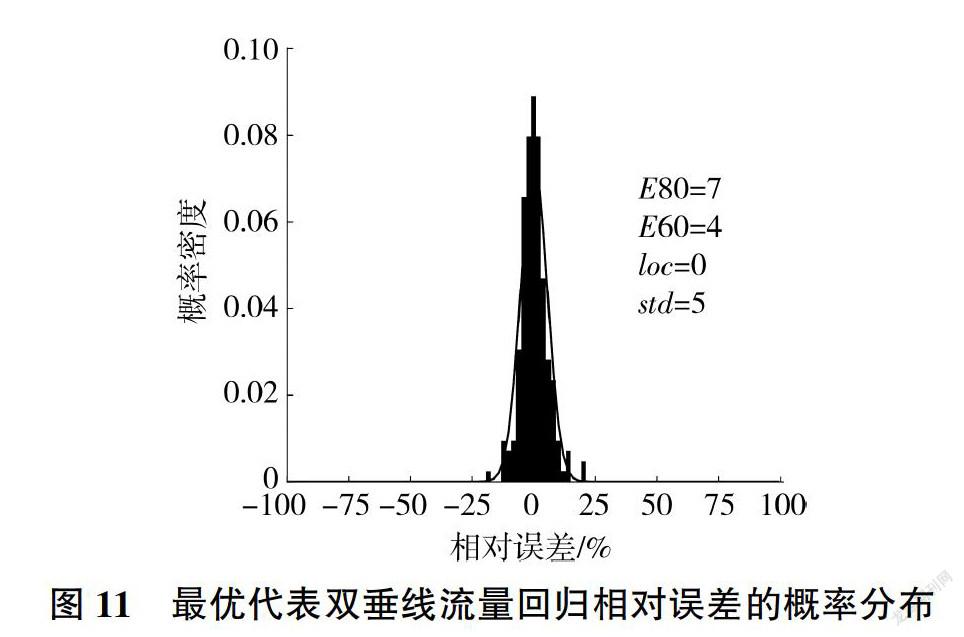
最優垂線位置（相對起點距20%和69%）見圖9，相應回歸檢驗結果及流量相對誤差的概率分布見圖10、圖11（E80、E60、loc、std分別為保證率80%對應的誤差、保證率600-/0對應的誤差、誤差均值、相對標準差）。

表2、圖9-圖11說明，若在龍門基上155斷面起點距分別為54、188 m處設置固定垂線實測流速和水深，使用式（3）來計算流量，則可以達到均方根誤差229 m/s、相對標準差5%的估算精度：

Q= 124.1 vld1+122.1 V2d2+165.7

（3）

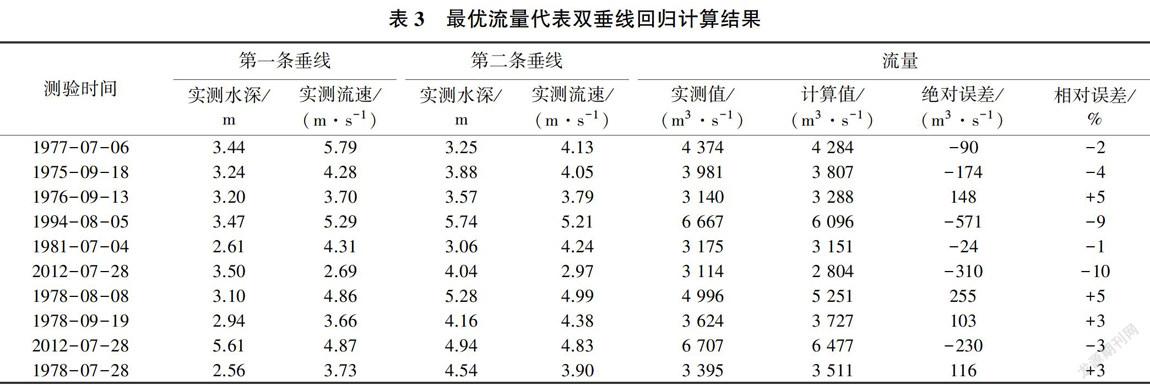
表3為在應用該最優解得到的回歸計算結果中隨機抽取10個測次的計算結果。

3 結語

（1）對于水深、流速、流量，使用兩條代表垂線的實測值，均可以較為準確地回歸計算相應的全斷面綜合值。

（2）水深代表單垂線的分析結果說明，單一垂線誤差較大，且由于位置出現在斷面中部，通常靠近中泓，因此不宜采用。

（3）從均方根誤差來看，代表垂線法仍有改進余地。增加垂線數量和輸人參數類別（如水位、河寬、預測流量級等）是兩種主要的改進途徑。

參考文獻：

[1] 中華人民共和國水利部，河流流量測驗規范：CB 50179-2015[S].北京：中國計劃出版社，2015：84-101.

[2] 王錦生，水文測驗手冊[M].北京：水利出版社，1980：228-237.

[3] 董禮瑋，陳河水文站代表垂線平均流速與斷面平均流速關系分析[J].陜西水利，2015，33（2）：186-188.

[4]張家軍，拓自亮，郭德成，受水庫調節影響的代表垂線法測流應用研究[C]∥第十二屆中國科學技術協會年會論文集：第二卷，北京：中國科學技術協會，2010：1-6.

[5] 錢學偉，劉少華，聲學多普勒測流原理及其應用[M].鄭州：黃河水利出版社，2003：56-78.

【責任編輯翟戌亮】