幼兒數學能力的發展趨勢及其影響因素：追蹤研究的證據

周靜嫻，楊寧

【摘要】本研究采用《家庭社會經濟地位問卷》《頭-腳-膝-肩任務》《學童數學成就測驗》對100名中班幼兒進行了一年半共3次的追蹤調查，應用多層線性模型分析幼兒數學能力的變化趨勢以及執行功能、家庭社會經濟地位對幼兒數學能力的影響。結果顯示：幼兒數學能力自中班下學期至大班下學期出現了顯著的增長趨勢，且存在個體差異；幼兒中班的初始執行功能水平能顯著預測大班階段的數學能力；幼兒中班初始執行功能水平對數學能力的增長速率存在顯著影響；家庭社會經濟地位對幼兒數學能力的預測效應不顯著。

【關鍵詞】幼兒數學能力；執行功能；家庭社會經濟地位

【中圖分類號】G612 【文獻標識碼】A 【文章編號】1005-6017（2019）07/08-0060-06

【作者簡介】周靜嫻（1992-），女，廣西柳州人，華南師范大學教育科學學院碩士研究生；楊寧（1963-），男，長沙人，華南師范大學教育科學學院教授，博士。

一、問題的提出

數學是幼兒學習與發展的重要領域之一，學前階段的數學發展水平能有效預測兒童后期正式入學的數學成績[1]，以及閱讀[2]、科學[3]等其他學習領域的表現。關于幼兒數學能力的發展，以往研究都證實了幼兒數學能力隨年齡而變化，與幼兒的成熟和經驗密切相關[4][5]，但關于幼兒數學能力發展的縱向趨勢研究仍甚為少見。在幼兒數學能力發展的影響因素研究中，認知因素占據主要地位，執行功能（Executive Function ，簡稱EF）被認為是重要影響因素之一。執行功能的主要結構包括工作記憶、抑制和認知靈活性，在多數生活情境中，三個成分共同協作以產生完整的執行功能。2～3歲是兒童執行功能發展的起始時期，同時也是數學能力發展的關鍵時期，執行功能水平低下，尤其是抑制控制和注意轉換能力弱是影響兒童早期數學低分和數學學習困難的重要原因[6]。在環境方面，家庭在幼兒數學能力發展中扮演著重要角色，不少學者開始關注家庭社會經濟地位對幼兒發展的影響。研究普遍認為家庭社會經濟地位（以下簡稱：家庭SES）由父母的受教育程度、收入和職業構成[7]，家庭SES越高，意味著該家庭能夠擁有更多的經濟資源和文化資源。根據美國國家數學委員會（The National Mathematics Advisory Panel）的報告，相比高收入家庭的兒童，來自于低收入家庭的兒童在數學上的整體表現較差，更容易出現數學學習困難[8]，而這樣的差異在學前教育階段就已經存在[9]。目前，我國在社會轉型中顯現出社會分層和流動的趨勢，來自不同階層家庭的幼兒能否獲得教育過程和教育結果的公平被認為是促進社會公平的關鍵，因此，家庭SES作為幼兒家庭背景的重要變量，它是否會影響幼兒的數學能力發展成為本研究探討的問題之一。

綜上可見，以往的研究已證實執行功能與家庭SES對幼兒數學能力發展具有重要意義。然而，目前我國針對幼兒數學能力的研究多停留在現狀調查以及影響因素上，缺乏長期縱向研究。本研究以幼兒數學能力發展及其執行功能、家庭SES的影響為研究主題，對幼兒進行了一年半的追蹤研究，應用多層線性模型（HLM）分析方法探討幼兒數學能力隨時間的發展趨勢及個體、家庭因素的影響機制。

二、研究方法

（一）研究對象

根據幼兒園等級、辦園性質等維度，通過分層隨機抽樣的方法，從廣東省廣州市選取10家幼兒園，其中省一級幼兒園3所、省二級幼兒園4所、省三級幼兒園3所；公辦幼兒園5所，民辦幼兒園5所。每家幼兒園隨機抽取1個中班的10名幼兒進行執行功能和數學能力的測查，共獲得100名幼兒樣本（男生48名、女生52名）。同時，對100名幼兒的父母進行家庭社會經濟地位調查。

（二）研究工具及施測過程

1. 研究工具

《家庭社會經濟地位問卷》采用師保國、申繼亮（2007）編制的家庭SES問卷[10]，家庭SES一般由父母親職業、受教育程度和家庭收入構成，但家庭收入的測量較為困難，通常不建議使用[11]。因而問卷根據職業分類的標準和學歷層次，對兒童父母職業、受教育程度進行編碼，兩部分所得值的總和作為家庭SES的指標值。

《頭-腳-膝-肩任務》（Head-Toes-KneeShoulder）[12]由Cameron等人編制，主要考察了兒童執行功能的抑制能力、工作記憶和認知靈活性三個成分。任務要求幼兒與主試口令反著做，當聽到主試說“摸摸你的頭”，幼兒要去摸摸他的腳；當主試說“摸摸你的腳”，幼兒要去摸摸他的頭；當主試說“摸摸你的膝蓋”時，幼兒要求摸摸他的肩膀，反之亦然。在第一部分10道題中，僅使用兩個提示詞（頭和腳）；第二部分的10道題中，也僅使用兩個提示詞（肩膀和膝蓋）；第三部分的10道題中，以上提及的四個提示詞都會使用上，每道題做錯記0分；自我更正記1分；正確記2分。最高分為40分。該任務評分者間一致性系數為0.98，信度較高。

《學童數學成就測驗》（Test of Children Mathematics Achievement）[13] 由謝如山（2014）編制，用于3～9歲幼兒的數學診斷。量表共120道題目，分為非正式數學思考與正式數學思考兩大領域。該量表內部一致性Cronbach’α系數為0.97，評分者間信度為0.96，可見信度較好；該量表采用幼兒數學分數作為效標，效標關聯系數為0.94，效度較好。

2. 施測過程

對幼兒運用《頭-腳-膝-肩任務》和《學童數學成就測驗》進行一對一施測，第一次測量（T1）時間為2015年5月（中班下學期）；第二次測量（T2）時間為2015年11月（大班上學期）；第三次測量（T3）時間為2016年5月（大班下學期），并在2015年5月，向幼兒家長發放《家庭社會經濟地位問卷》，發放問卷100份，回收問卷100份，回收率100%。

（三）數據處理

本研究采用SPSS19.0和HLM6.0對數據進行分析。在對個體進行追蹤、多次觀測的發展研究中，同一個體的不同次測量由于受同一個體共同特征的影響，有較大相似性，因而往往將這些數據看成是具有嵌套結構的，即測量嵌套于個體，通過HLM構建兩個數據層可以探究個體發展趨勢及個體間發展趨勢差異的問題[14]。本文分析中將要涉及的變量：

第一層變量

（1）數學能力：在一年半內被測查3次，是模型第一層方程中的因變量。

（2）時間：每次測試的時間點，從第一次到第三次被編碼為-2、-1、0，是模型第一層方程中的自變量。

第二層變量

（1）執行功能：第一次測試中幼兒執行功能得分，是模型第二層方程中的自變量。

（2）家庭SES：第一次調查中幼兒家庭SES得分，是模型第二層方程中的自變量。

三、研究結果

（一）幼兒數學能力發展趨勢

由表1和表2看出，隨著時間的變化，幼兒數學測驗分數有逐漸增長的趨勢，經方差分析，三次測量結果均存在極其顯著差異。并且，隨著時間的變化，幼兒個體間數學能力的差異漸漸縮小（標準差變小）。

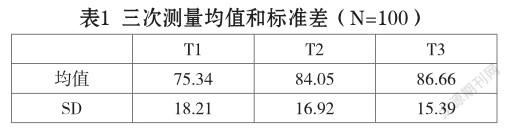
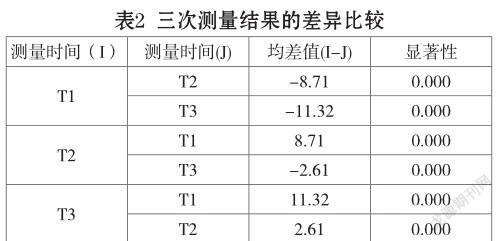
（二）數據的模型分析

1. 零模型分析

為檢驗研究假設，首先利用HLM的零模型（null model），它是分析的起點，能夠提供對組內相關系數的估計，以確認幼兒數學能力發展是否會因個體差異而有所不同。零模型設定如下所述。

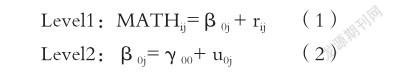
零模型的隨機效應被明確區分為level1和level2兩部分，分別代表幼兒數學能力的差異中源于時間變化的部分和源于個體之間差異的部分，即組內差異和組間差異。其中MATHij代表的是幼兒j（j=1，2…，100）的第i（i=1，2，3）次數學能力測量值；β0j是截距，即個體j的第一次測量值；rij是殘差，即個體j在第i次測量值與線性發展曲線的離差；γ00是平均截距，即第i次測量被編碼為0時所有個體的第i次測量的平均值；u0j 是個體j與平均截距的離差。模型分析結果表明個體間存在顯著的變異（SD=78.790，χ2=218.908，df=100，p<0.001），并且，組內方差為81.254，組間方差為89.339，則組內相關系數ICC（intra-class correlation）計算可得：

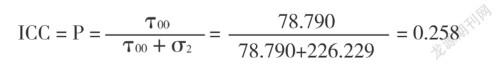
表明個體間的變異解釋了總體變異的25.8%。以往研究證明，當ICC>0.059時，表明有必要在研究中使用多層線性模型以處理個體水平變異[15]。

2. 無條件增長模型分析

無條件增長模型僅在第一層放入自變量，第二層為零模型，將第一層的回歸系數包含截距與斜率在第二層的回歸模型都設定為隨機效果，第一層模型可以描述個體隨時間的線性變化趨勢，而第二層模型即可解釋個體之間增長參數和斜率的差異，此模型旨在檢驗個體是否有線性變化的趨勢，以及這種線性變化是否存在個體之間差異的問題[16]。

隨機系數回歸模型設定如下，其中β1j表示線性增長率，即個體j在某個觀測值發展變化的斜率，γ10表示所有個體的平均發展速率。分析結果摘要如表3所示。

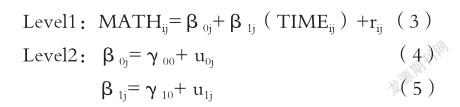
由表3可以看出，幼兒數學得分從中班上學期至大班下學期顯著增長（γ10=5.908，SE=1.052，t=5.615，p<0.001）。并且，截距和斜率在幼兒個體間的變異極其顯著（p<0.001），方差分別為89.111和25.887，這說明，大班下學期的最后一次數學測試分數在幼兒間差異顯著，幼兒數學能力的發展趨勢存在著顯著的個體差異，即幼兒數學能力增長的快慢有所不同。為了探討這種個體間差異的影響因素，需進一步分析個體變量特征對其幼兒數學能力變化的影響。

3. 全模型分析

全模型中不僅包含了第一層的時間變量，還加入了第二層的個體預測變量，這樣能夠通過理論建構來解釋幼兒數學能力的總體變異是怎么受到第一層和第二層因素影響的。根據研究假設，該部分主要考察個體的執行功能（EF）和家庭SES對幼兒數學能力的影響，以說明幼兒數學能力增長過程中，是如何受到個體差異的影響。

全模型設定如下，其中是γ01第二層方程的回歸系數，代表第二層的家庭SES和EF對第一層的截距β0j的效應；γ10是第二層方程的回歸系數，代表第二層的家庭SES和EF對第一層的發展斜率β1j的效應。分析結果摘要如表4（見下頁）所示。

結果表明，家庭SES對幼兒數學能力的預測效應不顯著（p>0.05），意味著盡管幼兒間的家庭社會經濟地位不同，但一年半后，他們的數學能力并不會有顯著差異，并且，幼兒數學能力發展的速率并不受家庭SES的影響。然而，初始執行功能對幼兒數學能力發展的截距預測效果極顯著（p<0.001），即初始執行功能較好的幼兒，到大班下學期，其數學能力也會較強；此外，執行功能對幼兒數學能力發展的斜率預測也極為顯著（p<0.01），說明初始執行功能發展水平不同的幼兒，數學能力的增長速率也存在顯著差異。

四、討論

（一）幼兒數學能力的發展趨勢

本研究分析表明，幼兒數學能力自中班下學期至大班下學期一年半的時間內出現了顯著的增長趨勢。這不僅支持了我國幼兒數學能力存在顯著年齡差異的橫向調查結果（兒童認知發展研究協作組，1982；趙振國，2009），同時也與周欣（2009）的一項縱向研究發現一致，即大班階段幼兒除部分數學能力仍在發展中，其他能力均顯著優于中班階段[17]。值得關注的是，中班下學期至大班上學期幼兒數學能力增長較快，而大班上學期至大班下學期進步較慢。

（二）執行功能對幼兒數學能力發展的影響

研究結果顯示，幼兒中班初始執行功能對幼兒數學能力增長的截距有顯著影響，即原執行功能水平較高的幼兒，其大班下學期表現的數學能力也較高。這與國內外眾多研究結果相一致（Bull，1999；Bull，2001；Espy，2004；Gathercole，2000；Gathercole，2004；McLean，1999；Passolunghi，2001），那些能夠更有效地在工作記憶中儲存信息、對刺激進行選擇性注意以及抑制無關信息的兒童取得的數學成就會更高。Bull（2001）指出4 歲兒童的工作記憶、抑制控制、計劃和監控技能對5～7 歲時的數學能力存在影響[18]。Blair（2007）發現兒童3歲時的抑制控制與 5 歲時的數學得分存在顯著相關[19]。執行功能是自我調控學習以及元認知能力的重要部分，其對幼兒大班后期的數學能力影響支持了Cunha（2007）的“能力促進能力”（skill-baget-skill）的假設，在受教育前期能力越強的幼兒，在后期習得的能力也越強[20]。

但研究結果還表明，執行功能初始水平的高低將影響幼兒數學增長的速率，即不同幼兒的數學能力水平的發展速率不同。這與國外研究一致，Blankson（2016）在一項ECLK-S兩年的幼兒數學能力追蹤研究中發現，幼兒2歲階段的執行功能水平在幼兒園至學前階段的數學能力增長中起到調節作用[21]。對于那些初始數學能力較弱的幼兒而言，較高的執行功能水平幫助他們在學習活動中保持最大化的投入，更易于在后期學前班階段取得更高的數學成就。我國自上世紀80年代末開始推行學前教育課程改革，在一日生活中加大了區域游戲的活動時間，強調自主探索的重要意義，部分教師卻受傳統集體主義觀念束縛，過分偏重集體教學活動，兒童主體地位有待提升。但值得注意的是，在數學領域，幼兒個體內部執行功能水平也許是兒童順利進入小學，促進早期數學能力發展的重要保障因素[22]。

（三）社會經濟地位對幼兒數學能力發展的影響

從研究結果來看，盡管幼兒來自不同社會經濟地位的家庭，但他們在大班下學期數學能力測試中的成績不存在顯著差異，并且，數學能力增長的速率也不會受到家庭SES的影響。盡管社會經濟地位在國外研究中普遍被認為對幼兒的數學能力發展具有較大影響，年幼孩子容易受貧困桎梏，造成階層的封閉循環。但在我國，這種影響并未達到統計學的顯著水平。這與國外眾多研究結果不一致（Baroody，1987；Klibanoff，2006；Starkey，1992；Tarullo，2008）。

目前我國關于幼兒社會經濟地位與數學能力的關系研究較少，研究結果支持周欣（2009）的發現，幼兒父母親的受教育程度并不能影響幼兒的數學認知發展。其原因可以下幾方面進行解釋：首先，部分研究表明盡管家庭SES是家庭背景中一個重要變量，但它對幼兒發展的影響可能會受到中介變量或調節變量的作用，而非直接影響幼兒發展。幼兒家庭背景還包括了家庭條件、藏書量等客觀條件，以及家長教育期待、家長教育態度與教育理念等主觀條件[23]，其中，父母對子女的教育期望影響著子女自身的教育期望和教育成就。在中國，隨著社會向市場化和現代化轉型，城鄉二元化、地區經濟發展不平衡等問題逐漸顯現，優勢家庭子女相比弱勢家庭也許能更便捷地獲得優質教育資源，但是，當不同背景兒童獲得同等學前教育機會時，社會經濟地位較低的家庭更有可能將教育看作是子女和家庭實現向社會上層流動的主要途徑，因而對子女期待更高，更重視幼兒的學業發展。其次，家庭環境除上述的家庭背景外，還包括家長與子女之間的互動關系，對于數學而言，家長尊重兒童學習興趣，與兒童一起閱讀、一起玩數學游戲等這些親子活動方式相比父母學歷而言更為重要（周欣，2009），調查的家庭中存在部分全職母親，盡管其按照職業等級評分較低，但卻更可能保證適宜的陪伴時間，保持高質量的親子互動關系，從而提高幼兒的數學能力。

五、教育建議

（一）正確看待社會經濟劣勢地位的兒童發展問題

當下，我國積極推行和諧社會，教育公平已成為教育學和社會學領域的研究熱點。過去普遍認為社會經濟劣勢地位的兒童在認知方面發展滯后，更值得注意的是，在如廣州等經濟發達地區還存在不少“流動兒童”，大眾往往會給他們貼上“問題兒童”“成績差”等標簽。但研究結果表明，父母學歷低、職業等級低并不會顯著影響兒童數學能力的發展，也就是說，低社會經濟地位的兒童盡管家庭物質、文化資源有限，但他們并不如輿論所述的那么糟糕，若監護人能夠盡心提供溫暖的家庭氛圍，那么孩子順利健康成長并不意外。因而，有必要以理性、客觀的態度給予處境不利兒童關注，避免“問題化”甚至“污名化”。

（二）重視童年早期執行功能的培養

初始階段執行功能水平較高的兒童將在后期數學能力發展上具有一定優勢，2～3歲是幼兒執行功能發展的開端，其培養和訓練通常需要一段時間才能夠見效，因此，家長可在親子互動中滲透執行功能的訓練。例如，傳統的“蘿卜蹲”游戲和研究中所采用的“頭-腳-膝-肩”游戲，能夠較好地吸引兒童興趣，同時，還應適當強調幼兒的生活常規，指導幼兒將用過的物品或玩具歸回原處，這些能夠有效地促進幼兒抑制控制和認知靈活性的發展。此外，家長也可通過設置游戲情境，與年齡較小的幼兒玩“錄音機說什么”的復述游戲，與稍大一些的兒童開展棋牌、拼圖等規則游戲，指導兒童有意識地進行記憶訓練。

（三）提供高質量的師幼互動

初始執行功能較高兒童在眾多研究中被認為會利用這些優勢而獲得更快速的數學能力增長，表現出“馬太效應”。幼兒教師既要鼓勵執行功能有優勢的幼兒發揮特長，也需耐心指導有潛能的孩子探索、游戲，通過高質量的師幼互動，保障執行功能在幼兒數學能力發展中能發揮關鍵的促進作用。因而，幼兒教師應時常審視自身在教育實踐中的行為表現，是否洞悉孩子們的個性特點，是否聽到了孩子們渴望的呼喚，是否看到了孩子們好奇的目光，盡量避免“支架”提供不及時、反饋質量不高、缺乏鼓勵和肯定等現象發生，做到有教無類，因材施教。

【參考文獻】

[1] Duncan， Greg J， Dowsett， Chantelle J， Claessens， Amy. School readiness and later achievement. [J]. Dev Psychol， 2007 （06）：1428-1446.

[2] Duncan J， Owen AM. Common regions of the human frontal lobe recruited by diverse cognitive demands. [J]. Trends in Neurosciences， 2000（10）：475-483.

[3] Sadler P M， Tai R H. Transitions. The two high-school pillars supporting college science.[J]. Science， 2007（27）：457-458.

[4] 兒童認知發展研究協作組.4-11歲兒童數學概念穩定性的發展的研究[J].心理學報， 1982（03）： 272-284.

[5] 趙振國.3～6歲兒童數感發展的研究[J].心理發展與教育， 2008（04）：8-12.

[6] 周欣，趙振國，李娟，等.認知因素對兒童早期數學學習困難的影響[J].學前教育研究， 2013 （11）：3-13.

[7] Buchmann C， Methodological Advances in Cross-National Surveys of Educational Achievement[M]. Washington， D C： National Academy Press，2002.

[8] US Department of Education. Foundations for Success： The Final Report of the National Mathematics Advisory Panel.[J]. Us Department of Education， 2008（09）：120.

[9] Klibanoff R S， Levine S C， Huttenlocher J. Preschool Children’s Mathematical Knowledge[J]. Developmental Psychology， 2006 （01）：59-69.

[10] 師保國，申繼亮.家庭社會經濟地位、智力和內部動機與創造性的關系[J].心理發展與教育， 2007（01）：30-34.

[11] 孫中欣.學業失敗問題的家庭社會經濟地位研究[J].清華大學教育研究， 1999（01）：47-51.

[12] Burrage M S， Ponitz C C， Mccready E A， et al. Age-and schooling-related effects on executive functions in young children： a natural experiment[J]. Child Neuropsychology， 2008 （06）：510-524.

[13] 謝如山.學童數學成就測驗指導手冊[M].新北：心理出版社，2014.

[14] [16] 劉紅云.追蹤數據分析方法及其應用[M]. 北京：教育科學出版社， 2005.

[15] A. S. Bryk， S.W. Raudenbush. Hierarchical Linear Models： Applications and Data Analysis Methods （Second Edition）[J]. Economics of Education Review， 1992 （03）：767-768.

[17] 周欣， 黃瑾， 趙振國，等. 大班兒童數學認知的發展[J].幼兒教育（教育科學）， 2009（11）：35-39.

[18] Bull R， Scerif G. Executive functioning as a predictor of children’s mathematics ability： inhibition， switching， and working memory[J]. Developmental Neuropsychology， 2001 （03）：273-293.

[19] Blair C， Razza R P. Relating effortful control， executive function， and false belief understanding to emerging math and literacy ability in kindergarten.[J]. Child Development， 2010（02）：647-663.

[20] Flavio Cunha， James Heckman. The Technology of Skill Formation[J]. The American Economic Review， 2007（02）：31-47.

[21] Blankson A N， Blair C. Cognition and classroom quality as predictors of math achievement in the kindergarten year[J]. Learning & Instruction， 2016 （04）：32-40.

[22] Caron A C，Verena E，Linanne J. Preschool executive function predicts early mathematics achievement[J]. Development Psychology， 2010（05）：1176-1191.

[23] 周皓. 家庭社會經濟地位、教育期望、親子交流與兒童發展[J].青年研究， 2013（03）：11-26.

本文系廣東省省級特色創新項目（教育科研類）“廣東省幼兒園教育質量評價：基于CLASS的研究”（項目編號：2014GXJK031）階段性研究成果之一。

通訊作者：楊寧，yang2007n@sohu.com

（責任編輯 張付慶）