基于多維博弈的多產品定價策略分析

謝會芹 景勤娟 李凡 李昌明

摘 要：根據多維博弈理論，探討具有需求替代性的多種產品定價策略靜態和動態多維博弈模型，然后求解其Nash多維均衡，最后比較多維博弈與單獨博弈均衡結果。并以河北省戰略性新興產業為例，具體研究該產業發展中的博弈與定價問題。

關鍵詞：多維博弈;定價策略;河北;戰略性新興產業

1.引言

在現實市場中，為了滿足消費者差異化需求，企業通常會提供多種相關產品，它們在功能定位、定價以及營銷策略上都存在著一定的差異性，許多學者對多產品定價問題圍繞著壟斷廠商進行了大量研究。但現實經濟活動中，企業的生產和銷售大多數是在競爭環境下進行的。此時，由于多產品之間可能存在著一定程度的需求替代性，為了獲得最大利潤，每個企業在選擇自己產品的定價策略時不僅要考慮競爭對手在該產品上的定價策略，還要同時考慮自己和對手在其它相關產品上的定價策略，這是一種多維博弈問題。

2.靜態博弈與動態博弈比較

假設某地區有兩個企業同時向當地市場提供種具有需求替代性的產品，并且壟斷了該地區這種產品的市場，企業的利潤函數為（其中：表示企業的第種產品的邊際生產成本）：

（1）

在靜態多維博弈中，兩個企業同時選擇定價策略向量，此多維博弈問題存在一個純策略Nash均衡[1]。企業的定價策略向量反應函數為

（2）

由式（2）可得維Nash均衡解為

（3）

其中：是階單位矩陣，A、B、D均可推算，推算過程略。

在動態多維博弈中，不失一般性，假設企業1（領頭企業）先行動，企業2（尾隨企業）再行動。通過最優一階條件，可得兩個企業關于種需求相關產品定價策略動態多維博弈的子博弈精煉維Nash均衡解。

3.多維博弈與單獨博弈均衡比較

在靜態博弈條件下，當只對第種產品進行定價策略靜態單獨博弈時，企業的利潤函數為

（4）

通過求解均衡發現，多維博弈下的維Nash均衡解分量與單獨博弈下的Nash均衡解完全一樣。因此，需求無關的種產品定價策略靜態多維博弈模型下的維Nash均衡解是個分別關于每一產品的定價策略靜態單獨博弈模型的Nash均衡解的簡單組合。

在動態博弈條件下，當只對第種產品進行定價策略單獨博弈時，利用逆序法[2]，可得到需求無關的種產品定價策略多維博弈的子博弈精煉多維Nash均衡解為，發現多維博弈下的子博弈精煉多維Nash均衡解式分量與單獨博弈下的子博弈精煉Nash均衡解和完全一樣。因此，基于種需求無關產品定價策略多維博弈模型的子博弈精煉多維Nash均衡解是個分別關于每一產品定價策略單獨博弈模型的子博弈精煉Nash均衡結果的簡單組合。

4.以河北省戰略性新興產業為例分析

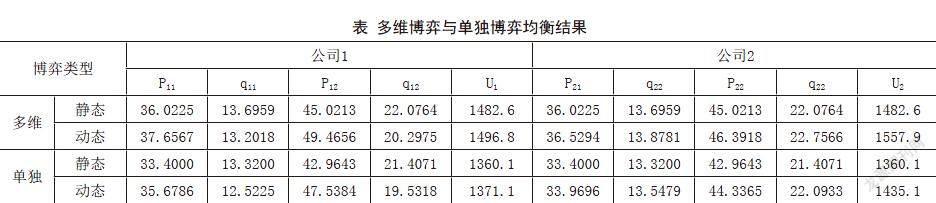
河北省兩家半導體照明材料公司分別向石家莊市場提供兩款照明材料，參數如下：，，，，，，，，，。由前面的分析可得多維博弈與單獨博弈均衡結果（如下表）。

通過分析可知，需求無關多產品定價策略靜態和動態單獨博弈是特殊情況;在動態多維博弈中，兩個公司的產品定價和利潤高于靜態多維博弈，其中，后動公司選擇低價策略并獲得更多市場份額和利潤，即后動公司具有后動優勢;多維博弈Nash多維均衡策略優于單獨博弈Nash均衡策略。

參考文獻

[1]Spence A M.Multi-product quantity-dependent prices and profitability constraints[J].Review of Economic Studies，47（150）：821-841.

[2]Maglaras C，Meissner J.Dynamic Pricing strategies for multiproduct revenue management problems[J].Manufacturing & Service Operations Management，2006，8（2）：136–148.

課題：2016年河北省社會科學基金項目（編號：HB16YJ052），2018年度河北省人力資源和社會保障課題（編號：JRS-2018-3036）