Chebyshev算子矩陣求解分數階微分方程的數值解

楊曉麗 許 雷

（1 內江師范學院生命科學學院；2 內江師范學院數學與信息科學學院 四川內江 641199）

分數階微積分是常微分和積分到任意階的推廣。與整數階相比，分數階微分方程在物理現象的模擬上有許多優勢[1]。近幾十年來，分數偏微分方程被廣泛用于描述工程過程和動力學系統。越來越多的研究人員致力于研究求解分數微分方程以及解的存在性和唯一性。由于分數階微分算子具有全局性以及對偶算子不是其負算子的性質，很難對分數階微分方程進行求解，因此很多學者對分數階問題的數值方法進行了研究。針對不同類型的方程提出了不同數值方法。常用的方法包括有限差分方法[2]，有限元方法[3]，譜Galerkin方法[4]以及正交多項式的方法。常用的多項式方法有Legendre多項式[5]、Chebyshev多項式[6]、Bernstein多項式[7]，以及Bernoulli多項式[8]。目前用Bernoulli多項式求解分數階微分方程的文獻很少，且運算較為復雜，因此基于分數階微分算子矩陣的方法，引入Chebyshev多項式，結合tau法和配方法將分數階微分方程轉化為線性或者非線性方程組，以降低問題的復雜性。

一、預備知識

（一）Caputo意義下的分數階微分[9]

定義1：Caputo類型的分數階微分定義

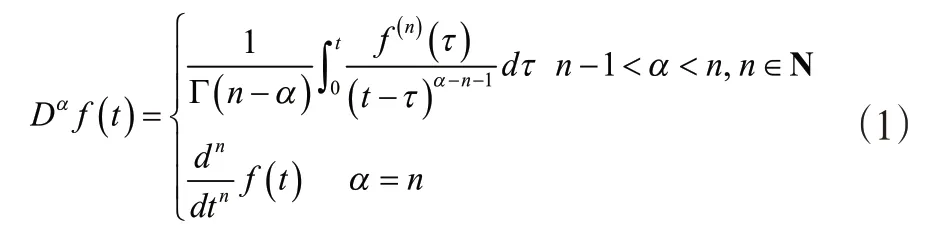
其中，α＞0，n是比α大的最小的整數，對于Caputo微分有DαC=0，C為常數

其中，γ和δ為常數。

（二）Chebyshev多項式的性質[10]

定義2：定義在[-1,1]上的Chebyshev 多項式為可由如下遞推公式得到：

移位Chebyshev多項式的解析解表示為：

滿足如下正交性：

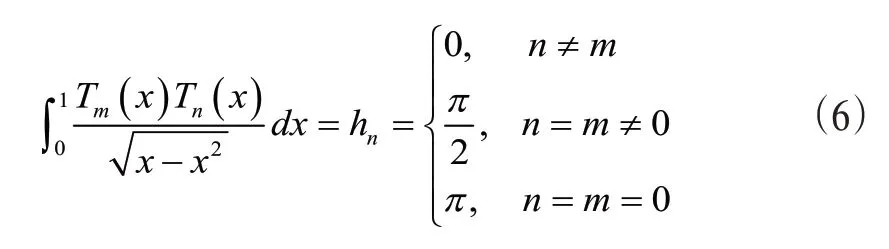
（三）Chebyshev 多項式函數逼近。設H=L2([0,1])Chebyshev多項式集合，γ=則對于H空間中的任意函數存在唯一的最佳近似g(t)∈γ：

式（7）等價于

其中，系數可以由如下公式得到，

在實踐中，只用前N+1項，即

二、分數階微分的Chebyshev算子矩陣

利用公式（12）得到，

引理1：設Chebyshev多項式，則

引理1 利用Caputo 微分的定義和公式（5）很容易證明，在此略。

定理1：設為移位Chebyshev向量，v＞0，

其中，D(v)為維的在caputo 意義上的分數階微分的運算矩陣，定義如下：

證明：

利用N+1項Chebyshev多項式逼近tk-v，得到

整理公式（18）（19）就可以得到證明的結果

三、數值計算方法

（一）線性分數階微分方程的求解。考慮Caputo意義下的分數階微分方程具有如下的形式：

初始條件滿足：

利用Chebyshev多項式可以將y(t)和ɡ(t)近似為：

其中，向量G可以由公式（10）求得，為未知向量，根據定理1，分數階微分可以做如下近似：

因此，公式（14）的殘差R(t)可以表示為：

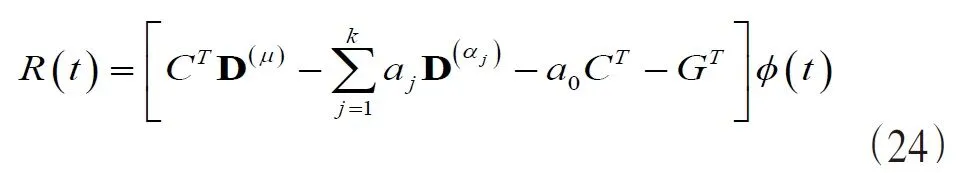
利用經典的Tau方法，我們可以利用如下公式產生維的N-m+1線性方程組：

利用初始條件可以得到，

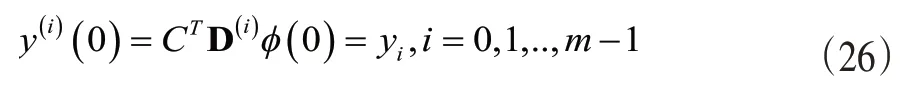
（二）非線性分數階微分方程的求解。對于如下的非線性分數階微分方程：

初始條件如（21）式,0＜q1＜…＜qk＜μ，則y(t),Dμy(t)，以及Dq jy(t)的近似處理和線性方程一樣，因此可以得到，

在配置點上，上述公式是完全相等的，因此選擇為N-m+1移位勒讓德多項式的根為配置點聯合初始條件得到N+1維的非線性方程組，利用典型的迭代方法，如牛頓迭代方法就能得到的近似解。

四、實例計算

例1：考慮如下非線性初值問題[11],

精確解為y(t)=t2

假設N=2，則方程的解可近似為：

因此可以得到線性方程組：

解得CT=[0.375 0.5 0.125]

例2：考慮如下邊界Bagely-Torvik問題[12],

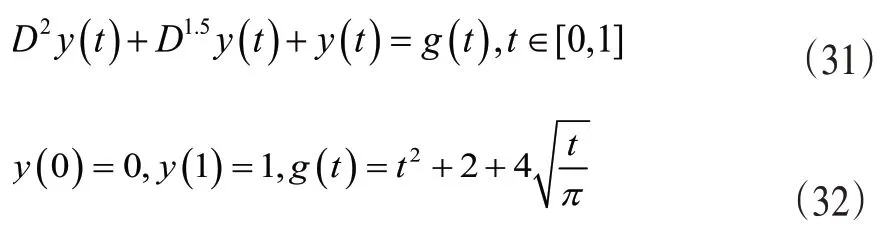
上述方程有精確解y(t)=t2

假設N=2，則方程的解可近似為：

對邊界條件進行處理得：

因此，利用3.1節的方法，同樣可以得到

五、結論

文本提出了解決一類分數階微分方程的Chebyshev矩陣方法。基于L2空間下，任意函數可由Chebyshev 多項式張開，將分數階的微分方法轉化為線性或者非線性方程組進行求解，降低了方程的計算復雜性，并通過實例分析證明了算法的有效性。