基于裂縫模擬的懸臂梁結構健康監測研究

那 磊

煤炭工業規劃設計研究院有限公司 北京 100120

1 前言

結構健康監測是一個監測結構損傷的過程，這一過程是利用傳感器采集結構動態響應數據來觀察結構狀態，從收集到的數據中提取出結構損傷的特征，進而，結構當前健康狀況可以通過對該特征分析來確定。由于結構損傷引起的結構特性變化對結構動力性能有影響，因此可以通過量化結構動力特性的變化來對結構損傷進行識別。此外，利用結構振動測試方法可以有效監測結構損傷。根據結構健康監測理論，結構特征的變化會引起模型監測數據參數的變化。

目前已有大量的研究利用理論計算對不同梁的固有頻率進行計算。本文旨在研究和分析線性和彈性懸臂梁的一階和二階固有頻率衰減與不同裂縫位置、寬度和高度之間的關系，利用有限元分析軟件ANSYS對不同裂縫參數引起的兩個固有頻率進行計算分析。進而，利用計算結果和相應變化關系作為基本數據庫，為今后評估裂縫位置和尺寸提供數據支持和理論依據，達到結構健康監測的目的。

2 建模分析及結果分析

2.1 模型建立及模態分析

結構健康監測概念和理論研究需要依靠一個合理的研究系統。基于振動的結構健康監測原理，本文設立一根一端固定一端自由的等截面矩形截面鋼懸臂梁模型，該梁長2m，寬0.2m，高0.2m，本次模擬為線性系統且處于彈性形變。該梁的彈性模量為2.068×1011 N/m，泊松比為0.33，容重為7850kg/m3。此外，建立一個有裂縫的懸臂梁模型，裂縫在靠近支座處的梁上表面。在模型中逐漸調整裂縫的位置、寬度和高度，以調查確定梁的固有頻率是否隨著不同裂縫參數改變。實際工程中，裂縫的幾何結構相對較復雜，為方便模擬，本文對裂縫形狀進行相應簡化處理。不同荷載引起的裂縫形狀基本為倒三角形，靠近支座處倒三角一側呈垂直狀，但在實際模擬中倒三角裂縫存在網格劃分問題，很難控制斜邊附近單元的網格密度。因此，將用等效矩形裂縫代替模擬真實倒三角裂縫形狀。這里用L表示裂縫與懸臂梁支座距離，W表示裂縫寬度，D表示裂縫高度。在模型中模擬裂縫的基本原理和途徑是局部剛度削弱，通過削弱裂縫處一個或一些單元的剛度來實現裂縫的模擬。

利用有限元分析軟件ANSYS對懸臂梁的裂縫進行模擬時，將采用PLANE 182單元代替BEAM 3單元，且將該懸臂梁模型視為二維模型。在ANSYS軟件中快速建立懸臂梁模型時，首先選擇相應的單元類型和是常數；其次建立材料模型，本項目中材料模型是彈性的和線性各向同性的；最后用關鍵點表示懸臂梁矩形截面的頂點。在此基礎上，削弱需要出現的裂縫位置處的單元剛度，實現裂縫的模擬。

2.2 ANSYS分析結果的收斂判別

2.2.1 無裂縫梁固有頻率的收斂判別

為了比較裂縫出現前后懸臂梁的固有頻率的變化，首先需要有無裂縫梁的固有頻率。在ANSYS軟件中，根據前一節所述的有限元分析方法，對模型進行網格劃分，進而分析出固有頻率值。然而，由于網格劃分密度沒有標準的判定標準，因此需要借助收斂判別方式。從有限元分析的觀點來看，系統單元越離散，結果就越準確。但是，當網格劃分密度到達一定臨界值后，結果的變化會越來越小，可以忽略不計。因此，為了完成無裂縫梁固有頻率的收斂判別，首先設定網格尺寸為0.1×0.1m，得到前兩階固有頻率，隨后逐漸減小網格尺寸至最小尺寸為0.005×0.005m，得到相應的前兩階固有頻率值，見表2.1。

表2 .1 不同網格尺寸情況下無裂縫梁前兩階固有頻率

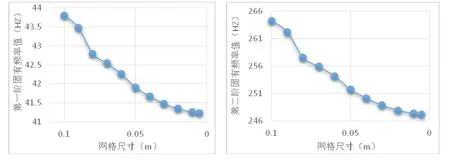
圖2 .1 無裂縫梁第一階和第二階固有頻率收斂

從圖2.1可看出前兩階固有頻率隨著網格尺寸劃分不同而變化，在初始階段，當網格尺寸較大時，前兩階固有頻率的變化相對較明顯，然而隨著網格尺寸越來越小，在相應位置圖形切線的斜率逐漸減小并趨近于零，圖形收斂到水平漸近線。換言之，這時固有頻率的減小量可忽略不計。因此，無裂縫梁的前兩階固有頻率值分別為41.265Hz和247.40Hz。

2.2.2 有裂縫梁固有頻率的收斂判別

懸臂梁的裂縫形式種類繁多，包括不同的裂縫位置、裂縫寬度和高度，也將對應不同的第一與第二階固有頻率。選取幾個典型的裂縫參數進行相應的固有頻率收斂判別，若選取的裂縫參數對應的臨界網格尺寸相同，則可判定該網格尺寸可適用于其他不同裂縫參數。本節選取以下三種裂縫參數進行分析研究:（1）懸臂梁裂縫參數：位置L為0.040m，寬度W為0.010m，高度為0.020m；（2）懸臂梁裂縫參數：位置L為1.000m，寬度W為0.025m，高度為0.100m；（3）懸臂梁裂縫參數：位置L為1.800m，寬度W為0.050m，高度為0.050m。采用上述裂縫參數，利用ANSYS軟件分析對應的第一與第二階固有頻率，結果見表2.2。

表2 .2 三種裂縫參數情況下第一階和第二階固有頻率

根據表格顯示，無論采用那種裂縫參數，前兩階固有頻率的變化趨勢大致相同，且三種裂縫參數下兩個固有頻率的臨界網格尺寸均為0.01m。因此，從邏輯上可推斷出任何裂縫的臨界網格尺寸應為0.01m。

2.3 固有頻率與裂縫位置、寬度及高度變化的關系

本節在設置裂縫的位置、寬度或高度為唯一變量的情況下，利用ANSYS軟件計算分析出相應的固有頻率值，各唯一變量的設置及對應固有頻率值詳見表2.3。通過結算結果可以分析并建立各唯一變量與前兩階固有頻率間的變化關系圖（此處省略圖表），不難發現，裂縫寬度和高度越大，前兩階固有頻率越小，而裂縫離支座端越遠，第一階固有頻率越大，第二階固有頻率則呈正弦波型，在0.5m和1.9m處為波峰，在0.05m和1.0m處為波谷。

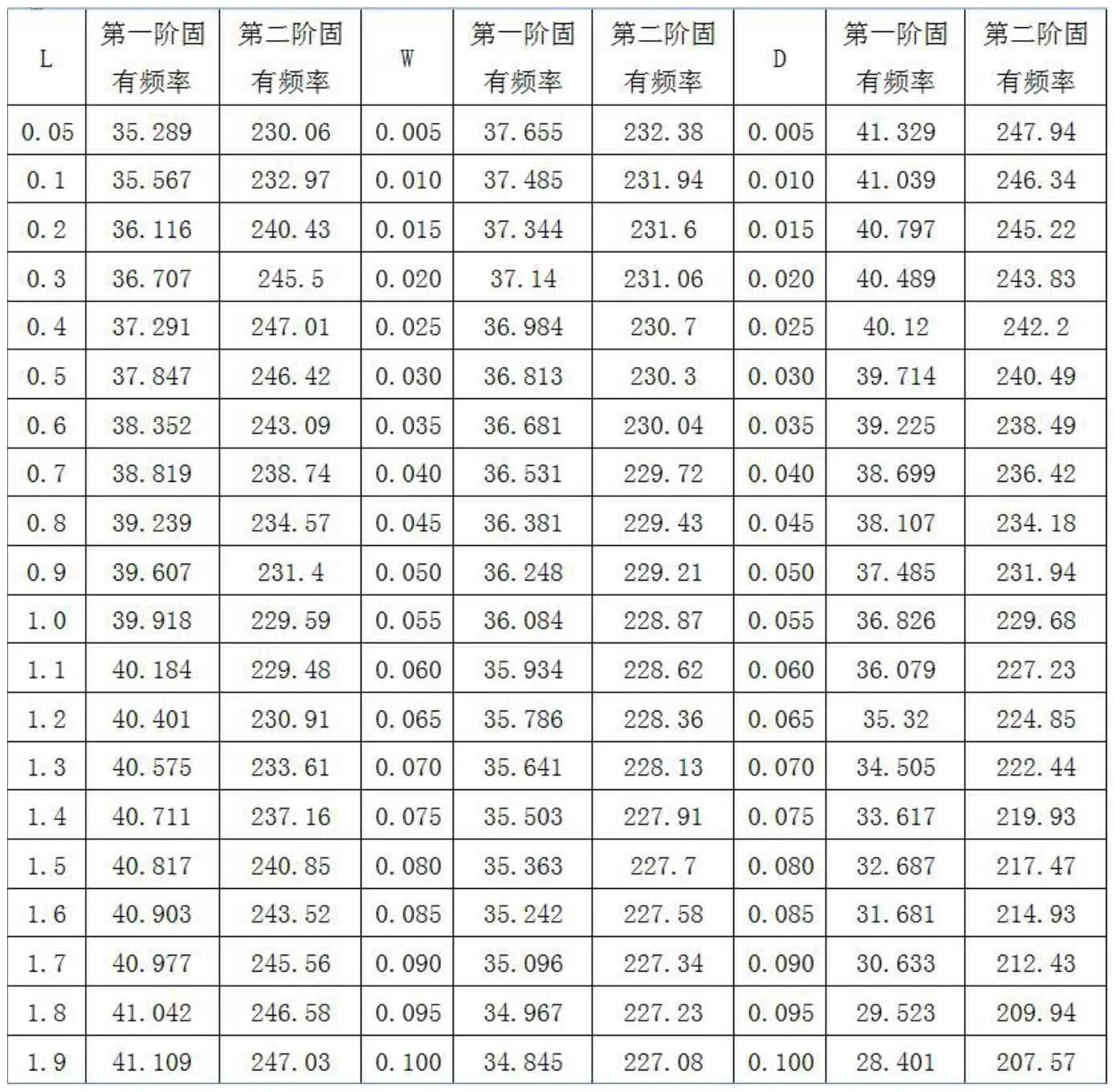
表2 .3 不同裂縫參數對應的第一與第二階固有頻率值

為更直觀的表達裂縫出現前后固有頻率的變化，通過引入固有頻率折減的概念（即出現裂縫后與出現裂縫前的固有頻率比值），依據上述分析結果，可建立單一裂縫變量與固有頻率折減的關系。另外，為方便表達，定義一些符號，例如分別為裂縫距離（L）為單一變量時裂縫出現后、裂縫出現前第一階固有頻率值，其余符號定義規則類同。根據ANSYS計算結果，繪制出關系圖見圖2.2～2.4。結果表明，隨著裂縫位置與支座端距離的增大，第一階固有頻率折減增大，此外，第二階固有頻率折減的變化呈正弦波形，但與之不同的是在第二個波谷后折減量不再減小；裂縫寬度增大與第一階、第二階固有頻率折減均呈線性關系，而第二階固有頻率的折減比第一階要小，折減變化率也低；而隨著裂縫高度增大，第一階固有頻率折減變化趨勢呈類拋物線狀，且折減變化率越來越大，第二階固有頻率折減與裂縫高度變化的關系基本呈直線，有類拋物線的趨勢。

圖2 .2 裂縫位置變化與固有頻率折減的關系

圖2 .3 裂縫寬度變化與固有頻率折減的關系

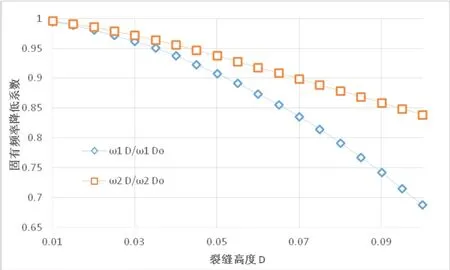
圖2 .4 裂縫高度變化與固有頻率折減的關系

此外，在分析單一裂縫參數變量與固有頻率折減的關系的基礎上，為更全面地反映不同裂縫對固有頻率折減的影響，可以延展至兩種裂縫參數共同變化對固有頻率折減的影響（此處忽略圖表）。經過分析，當裂縫寬度和高度同時增加時，固有頻率均會折減，但第一階固有頻率折減程度較第二階更大，換言之，相同的裂縫參數下，第一階固有頻率折減較第二階更嚴重。另外，隨著裂縫高度的增加，裂縫寬度相對較大的梁第一階和第二階固有頻率的折減速度高于裂縫寬度較小的梁。但是研究發現，相對于裂縫寬度較大的梁，裂縫寬度較小的梁的第二階固有頻率折減量明顯較大。除此之外，對于任何裂縫寬度和高度，隨著裂縫距離支座端的距離增加，第一階固有頻率均會減小，然而第二階固有頻率不會隨裂縫距支座端的距離增大而連續減小。綜上所述，當裂縫位置確定時，第一階和第二階固有頻率的變化足以用來進行裂縫寬度和高度的識別，然而由于固有頻率變化的隨機性，還不足以對裂縫位置進行估計和識別。因此，未來的研究可致力于評估不同裂縫位置損傷結構的前三階或更多固有頻率上，用更多的結構特性參數數據支撐結構健康監測體系。

4 小結

本文中提到的分析過程為結構健康監測的逆程序，該程序為利用所提供的裂縫位置、寬度和高度評估結構的固有頻率，從而可根據裂縫梁的固有頻率值評估裂縫的位置、寬度和高度，進行反向推導。該程序可推廣并應用在結構健康監測中。然而，這個方法有一定局限性，第一裂縫位置在現有研究數據中很難評估，第二由于ANSYS軟件網格劃分的操作誤差，在裂縫相對較小的情況下固有頻率的變化很難準確量化。這些問題是我們今后研究的重點。