軸對稱推力矢量控制伺服機構空間運動解耦研究*

劉 海，張新華，段小帥，肖中卓，周 圍，霍希建

(北京自動化控制設備研究所·北京·100074)

0 引 言

推力矢量控制(Thrust Vector Control, TVC)技術[1-4]是一種按照產生控制力和控制力矩的方式定義的航天器飛行控制方式，它通過改變發動機尾噴流方向來控制飛行器的飛行方向和姿態角的變化，使飛行器具有更高的機動性和敏捷性。軸對稱推力矢量控制系統主要由2個90°分布的機電伺服機構和控制器組成[5-7]，如圖1所示。其最大的特點是兩個執行機構需要協同運動才能夠使得噴管滿足擺動角度的需求。當兩個伺服機構的下支點與噴管的下支點不在同一平面時，兩伺服機構的位移會產生牽連耦合[8]。以往，矢量噴管姿態與推力矢量伺服機構的運動規律間的關系往往通過平面投影幾何計算，建模困難[9]。本文提出了一種利用歐拉角描述噴管姿態、通過空間齊次坐標變換矩陣原理對兩路噴管伺服機構進行空間位移計算的空間解耦計算方法。

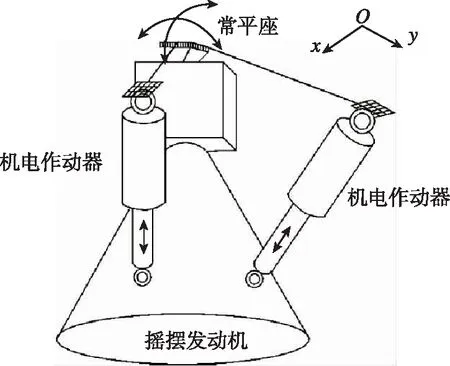
圖1 噴管軸對稱推力矢量控制系統Fig.1 Symmetrical thrust vector control system of nozzle

1 理論建模分析

1.1 空間歐拉角描述

歐拉角的物理概念直觀，特別適合于描述物體的空間姿態。歐拉角的示意圖如圖2所示，做定點轉動的物體有三個自由度，對應的三次任意有限轉動均可描述物體在固定坐標系下的空間姿態。設固定坐標系為OXYZ，隨動坐標系為oxyz。初始時，兩坐標系重合，OXYZ坐標系先繞Z軸轉動ψ角得到ox0y0z0，再繞x0轉動角θ得到ox1y1z1，最后繞z1轉動角φ得到oxyz。上述三次轉動均為相對坐標變換，相互獨立，任一次的轉動都不影響其他轉動的值。歐拉角可表示為(ψ，θ，φ)。

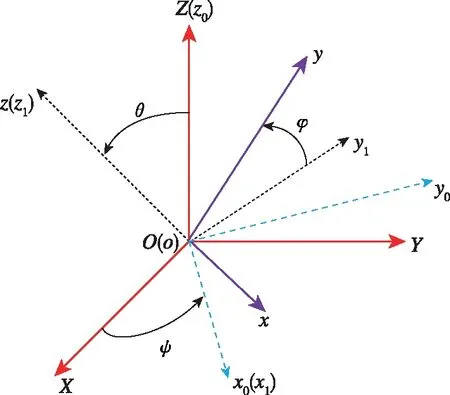
圖2 歐拉角示意圖Fig.2 Euler angle diagram

將歐拉角以方向余弦矩陣表示為

A=AψAθAφ

(1)

式(1)中，Aψ為OXYZ到ox0y0z0的變換余弦矩陣；Aθ為ox0y0z0到ox1y1z1的變換余弦矩陣；Aφ為ox1y1z1到oxyz的變換余弦矩陣。

1.2 軸對稱推力矢量控制伺服機構空間模型建立

軸對稱推力矢量控制伺服機構的布局如圖3所示。在描述噴管的運動學特征時，首先確定了整體系統是一個二自由度結構，并且只發生旋轉且不會發生自旋，很適合用歐拉角來描述[10]。在飛行器上建立固定坐標系OXYZ，在噴管與地面鉸接點建立隨動坐標系oxyz。初始時，兩個坐標系重合。單噴管的三維姿態參數包括θ、φ，其定義分別如下：θ為目標中軸線與固定坐標系水平面OXY的夾角；φ為目標中軸線在固定坐標系水平面OXY上的投影與OX軸正方向之間的夾角。采用歐拉角描述擺動噴管的姿態，歐拉角為(φ,θ，-φ)。

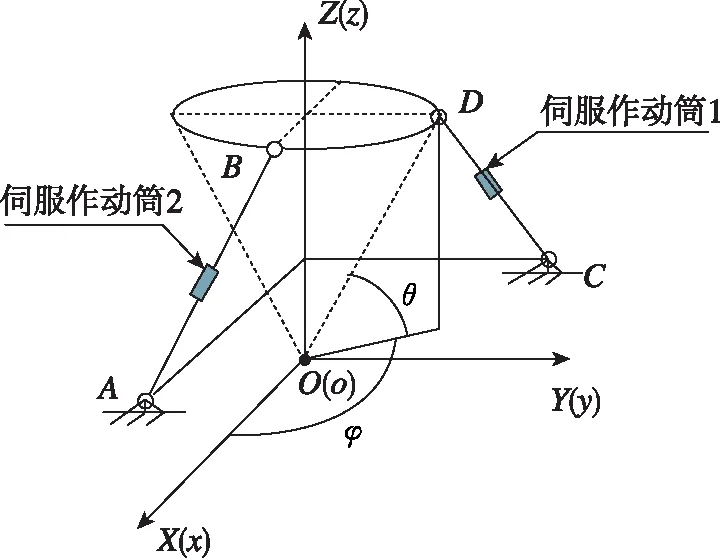
圖3 軸對稱推力矢量控制伺服機構的布局Fig.3 Axisymmetric thrust vector control servomechanism layout

由固定坐標系OXYZ變換到噴管上隨動坐標順序為OXYZ并繞其Z軸轉動角φ，得到新坐標系ox0y0z0。ox0y0z0繞其x0軸轉動θ角，得到新坐標系ox1y1z1。ox1y1z1繞其z1軸轉動-φ角，得到oxyz。由歐拉角轉換為方向余弦矩陣，即有

(2)

式(2)中：

A11=cos(φ)cos(-φ)-cos(θ)sin(-φ)sin(φ)
A12=-sin(φ)cos(-φ)-cos(θ)sin(-φ)cos(φ)
A13=sin(θ)sin(-φ)
A21=cos(φ)sin(-φ)+cos(θ)cos(-φ)sin(φ)
A22=-sin(φ)sin(-φ)+cos(θ)cos(-φ)cos(φ)
A23=-sin(θ)cos(-φ)
A31=sin(θ)sin(φ)
A32=sin(θ)cos(φ)
A33=cos(φ)

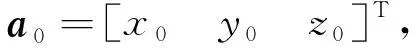
(3)

1.3 軸對稱推力矢量控制伺服機構運動程序計算

A鉸點在固定坐標系OXYZ中的坐標為(440, 0, 542)，C鉸點在固定坐標系OXYZ中的坐標為(0, 440, 542)；B鉸點在隨動坐標系oxyz中的坐標為(436.5, 0, 110)，D鉸點在隨動坐標系oxyz中的坐標為(436.5, 0, 110)。φ的范圍為0°～ 360°，θ的范圍為0°～ 7°。

伺服機構AB的位移解算結果如表1所示，伺服機構CD的計算結果如表2所示。

計算結果顯示，當角φ為0°、角θ由0°變化至7°時，伺服機構AB與角θ在同一平面內，伺服機構AB的位移由432.0142mm變化為486.0614mm，與角θ垂直的平面伺服機構CD的位移同時由432.0142mm變化為433.0146mm。這說明當兩個伺服機構的下支點與噴管的下支點不在同一平面上時，兩伺服機構的位移會產生牽連耦合。同時，計算結果給出了伺服機構AB與CD隨角φ和角θ同時變化的位移結果，通過數值插值可將其用于系統控制。

表1 LAB伺服機構的位移數據

表2 LCD伺服機構的位移數據

2 基于虛擬樣機ADAMS的仿真分析

2.1 仿真模型建立

基于UG和ADAMS協同仿真，建立軸對稱推力矢量控制伺服機構的仿真實體模型，如圖4所示。在模型中，將機架固定在大地上，忽略桿件連接中的銷軸，以轉動副替代。分別對部件添加約束條件，約束條件主要包括機架與大地間的固定副、噴管與地面間的球副、電動伺服系統執行機構鉸點與機架間的轉動副、電動伺服系統執行機構鉸點與噴管間的轉動副、電動伺服系統執行機構內部的滑動副。

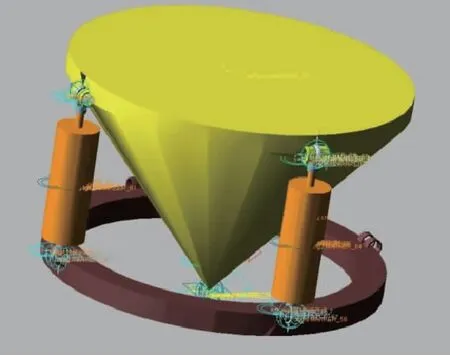
圖4 軸對稱推力矢量控制伺服機構的仿真實體模型Fig.4 Axisymmetric thrust vector control servo mechanism simulation entity model

2.2 仿真結果分析

本仿真需要驗證給定噴管姿態，反求伺服機構的輸出位移。因此，需通過驅動噴管實現在不同角φ(0°、45°、90°)下，角θ由0°變化至7°，變化步長為0.15°。經分析，得到伺服機構AB和伺服機構CD對應的位移曲線如圖5所示。

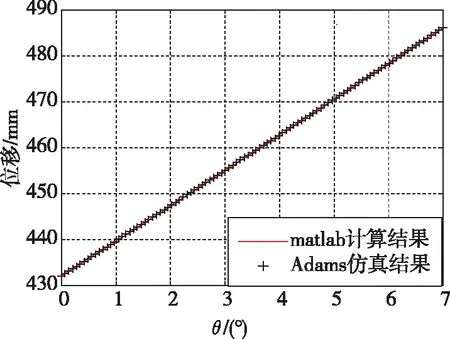
(a)角φ為0°時伺服機構AB的位移

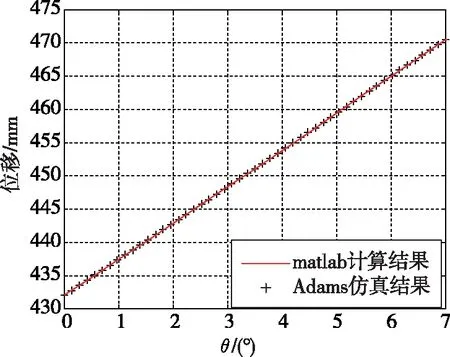
(c)角φ為45°時伺服機構AB的位移

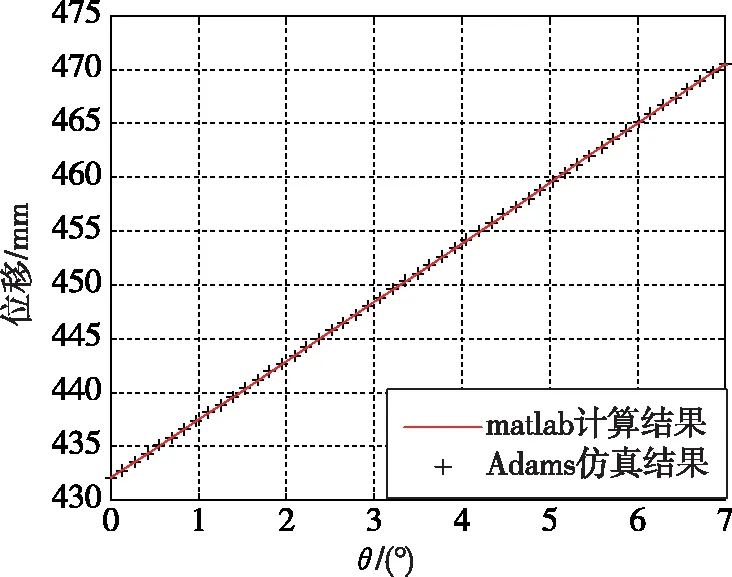
(d) 角φ為45°時伺服機構CD的位移

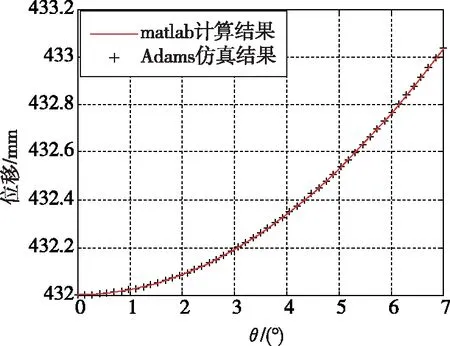
(e) 角 φ為90°時伺服機構AB的位移

(f) 角φ為90°時伺服機構CD的位移圖5 ADAMS仿真結果與Matlab計算結果對比Fig.5 Comparison between ADAMS simulation results and Matlab calculation results

對比ADAMS虛擬樣機的仿真結果與Matlab的計算結果，在不同角φ(0°、45°、90°)下，角θ由0°變化到7°時，兩種結果的趨勢完全一致，且兩種結果顯示的伺服機構絕對位移誤差均不大于0.0012mm。

3 結 論

針對矢量發動機噴管的兩個伺服機構間的運動牽連效應問題，本文提出了一種新型空間解耦計算方法。該方法利用歐拉角描述噴管姿態，通過空間齊次坐標變換矩陣原理對兩路噴管伺服機構進行了空間位移解耦計算，得到了兩伺服機構的伸長量解析解，并通過ADAMS虛擬樣機建模驗證了單擺雙噴管伺服機構空間解耦計算方法的正確性，實現了對噴管擺動方向和擺動角度的精確控制。