基于IVSSTLMS算法的數(shù)字域共址無線收發(fā)設備互擾對消

郝學坤，劉建成,2

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081 2.中國人民解放軍31634部隊，云南 昆明 611731)

0 引言

21世紀是信息時代，人們對信息需求量越來越大，可用的無線頻譜資源日益緊張。無線通信因其本身的機動性和靈活性已成為主要通信方式，比如超短波無線電臺、微波中繼和衛(wèi)星通信。然而，隨著無線通信設備數(shù)量急劇增加，在有限的物理空間和頻譜范圍內，大量無線收發(fā)設備同時工作將不可避免地產(chǎn)生相互干擾，比如陸基戰(zhàn)術指揮車和海上大型艦船上的眾多型號和頻段的電臺、雷達等，構成了復雜的電磁環(huán)境。

為抑制共址無線收發(fā)設備間互擾，研究者們提出利用已知的發(fā)送信號構建干擾，再將其從接收信號中減去的干擾對消方法，能夠有效解決微波同頻中繼收發(fā)互擾[1-3]，戰(zhàn)術超短波同車電臺互擾[4-7]，同時同頻全雙工(Co-time and Co-frequency Full-duplex, CCFD)收發(fā)自干擾[8-16]和衛(wèi)星中繼收發(fā)[17]等問題。該方法不需要犧牲任何頻譜資源，僅需在接收天線與預選濾波中間加入對消裝置，對收發(fā)設備的結構特性無特殊要求。根據(jù)干擾對消所處理信號的形式，可將其分為射頻域干擾對消和數(shù)字域干擾對消。

數(shù)字干擾對消通常是在射頻干擾對消之后進行，利用已知的基帶信號，在數(shù)字域通過信道估計和自適應濾波等方法有效估計干擾信號，進而消除基帶接收信號中的射頻對消殘余干擾，提高系統(tǒng)的對消比。比如文獻[9]和[14]將射頻干擾對消和數(shù)字干擾對消結合，較好地解決了CCFD系統(tǒng)的自干擾抑制問題。

文獻[14]基于最小二乘(Least Square, LS)估計，利用等間隔的時域導引序列估計信道響應，再將已知的基帶信號與信道響應卷積，得到重構的干擾信號。為在射頻域高對消比基礎上，進一步提高數(shù)字域干擾對消性能，文獻[9]利用WiFi中OFDM信號每幀的導引序列估計出自干擾信號參數(shù)，不過該方法受限于幀結構的導引序列設置，且采用的LS估計性能有限。文獻[16]基于文獻[14]和文獻[9]的數(shù)字干擾對消架構，提出最大似然信道估計的干擾對消方法，當期望信號與干擾功率之比(Signal-to-Interference Ratio, SIR)為-55 dB時，與文獻[14]和文獻[9]相比性能提高約10 dB，但隨著SIR增大至-35 dB，對消比基本相同。文獻[12]提出基于最小均方誤差的直通和共軛兩路信道參數(shù)估計方法，進而實現(xiàn)寬帶自干擾信號的數(shù)字對消，不過該方法同樣需要導引信號，且不能實時跟蹤信道的變化。文獻[15]和文獻[18]提出一種新的數(shù)字干擾對消方案，該方案在干擾機發(fā)射天線之前耦合參考信號，利用接收機的本振對參考信號下變頻，將信號轉換至基帶，再采用信道估計的方法重構干擾信號。該方法性能與文獻[14]相比，對消比提高10 dB以上，但需要附加的射頻通道，跟蹤信道變化的能力弱。文獻[19]利用常規(guī)定步長LMS算法實現(xiàn)CCFD數(shù)字干擾對消，但該方法未解決參考信號自相關矩陣特征值發(fā)散的問題，致使收斂速度慢。文獻[20]采用遞推最小二乘(Recarsive Least Square,RLS)自適應濾波方法實現(xiàn)數(shù)字干擾對消，能夠獲得約26 dB對消比，同時與文獻[19]相比提高了收斂速度，但該方法同樣不能消除干擾的非線性分量，且計算復雜度高。文獻[2]基于LMS算法，提出基于譜成型的自適應數(shù)字干擾對消方法，應用于全雙工中繼通信，但該方法所需計算量大，并未解決LMS算法收斂速度與互擾對消比相互制約的問題。

由上述分析可知，針對共址無線收發(fā)設備的數(shù)字域互擾對消，基于LS信道估計的方法需求解逆矩陣，計算復雜度高，且不能夠實時地跟蹤信道變化，而基于LMS和RLS算法的互擾對消方法存在收斂速度與互擾對消比相互制約的矛盾。本文針對此問題，提出基于迭代變步長變換域最小均方算法(Iterative Varging Step-Size Transform Least Mean Square,IVSSTLMS)算法的數(shù)字域共址無線收發(fā)設備互擾對消方法。

1 數(shù)字域互擾對消

現(xiàn)有的數(shù)字域干擾對消方法主要是通過信道估計的方法，估計出離散互擾信道響應h(n)，再將已知的基帶發(fā)送信號s(n)與h(n)進行離散卷積，得到重建的基帶互擾信號sc(n)，進而從接收的基帶信號r(n)中減去，最終完成數(shù)字域互擾對消。

數(shù)字域干擾對消基本原理如圖1所示，對于離散信道響應h(n)的估計，文獻[14]和文獻[16]分別提出最小二乘LS、最大似然(MaximumLikelihood, ML)和頻域LS法。

圖1 數(shù)字域互擾對消原理框圖Fig.1 Digital mutual-interference cancellation principle block diagram

暫不考慮殘余的非線性干擾抑制，假設互擾信道響應的階數(shù)等于M，接收的基帶信號r(n)可表示為：

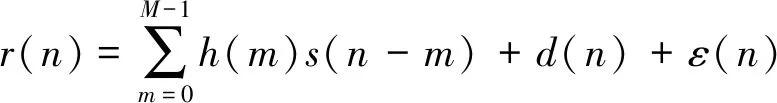
(1)

式(1)中，d(n)表示遠端發(fā)給接收設備的期望信號，ε(n)表示噪聲。

將信道響應h(n)、r(n)、d(n)和ε(n)以矢量形式表示：hM=[h(0)h(1) …h(huán)(M-1)]T，rM(n)=[r(n)r(n-1) …r(n-M+1)]T，dM(n)和εM(n)的形式同rM(n)，式(1)可轉化為：

rM(n)=SM(n)hM+dM(n)+εM(n)

(2)

式(2)中，SM(n)為基帶發(fā)送信號s(n)構造的托普利茲(Toeplitz)矩陣，即：

(3)

由式(2)和式(3)可得數(shù)字域互擾信號sI(n)與參考信號s(n)、信道響應矢量hM的關系：

(4)

式(4)中，sM(n)=[s(n-M+1)s(n-M+1) …

數(shù)字域干擾對消旨在利用已知的發(fā)送信號s(n)和接收信號r(n)，估計互擾信道響應矢量hM，進而消除r(n)所包含的互擾信號sI(n)。當互擾為帶內線性分量，可采用計算簡單的LMS自適應算法遞推求解信道矢量hM，再引入迭代變步長思想[21]，進一步加快收斂速度，減小穩(wěn)態(tài)失調誤差。

因基帶參考信號s(n)是調制符號經(jīng)成型濾波輸出，其自相關矩陣的特征值發(fā)散[22]，所以需對LMS算法的參考信號做變換處理，即TLMS算法，使得參考信號具有良好的平穩(wěn)特性。

2 基于IVSSTLMS算法的數(shù)字域互擾對消

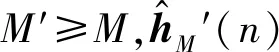
(5)

式(5)中，μmin是設定的最小值，μmax是設定的最大值，κ為調整參數(shù)，控制了μ(n)隨n變換的快慢，m是步長因子改變的起始時刻，初始值為0。

在此基礎上，基于IVSSTLMS算法的數(shù)字域互擾對消模型如圖2所示。

該對消方法的基本流程如下：

1) 算法初始，根據(jù)已知信號s(n)及先驗知識，確定M′，保證M′不小于互擾信道等效階數(shù)，信道響應向量初值為0，設定修正因子δ，步長因子最大最小值μmax、μmin和參數(shù)κ，遞推次數(shù)的初始值m=0，n由0起始；

2) 由M′和λ計算變化矩陣TM′和對角矩陣ΛM′；

3) 根據(jù)1)中參數(shù)計算步長因子μ(n)，之后執(zhí)行式(6)、式(7)和式(8)；

4) 估計當前時刻誤差e(n)的功率大小，與前k時刻e(n-k)比較，二者之差若大于設定門限γ，則執(zhí)行步驟5)，小于則直接返回執(zhí)行步驟3)；

5) 將當前的遞推次數(shù)n賦值給m，返回執(zhí)行步驟2)。

其中，γ設為接收信號功率3～5倍，e(n)功率估計等價求k個值平均。

上述對消過程的數(shù)學描述如下：

xM′(n)=TM′sM′(n)

(6)

(7)

(8)

式(6)—式(8)中，TM′為算法的M′×M′維變換矩陣，xM′(n)為變換后的參考信號向量，e(n)為對消后信號，ΛM′(n)為M′×M′維對角陣。

(9)

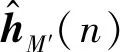
3 性能分析及仿真

為進一步分析提出方法的性能，本節(jié)從理論上推導其收斂性和能夠獲得的MICR，同時對比分析該方法與基于現(xiàn)有變步長LMS、RLS及LS信道估計對消法的計算復雜度，并進行仿真驗證。

3.1 收斂特性

IVSSTLMS算法建立在最小均方誤差準則基礎上，是對維納解的遞推求解。所以，分析基于IVSSTLMS算法的數(shù)字域互擾對消性能，可參考LMS算法分析，不同之處在于變化矩陣和對角陣的處理。

e(n)=[cM(n)]HxM(n)+u(n)

(10)

式(10)中，u(n)=d(n)+ε(n)，其均方誤差為σ2=E{|u(n)|2}。

因互擾與期望信號、噪聲不相關，對消誤差信號的均方值可表示為：

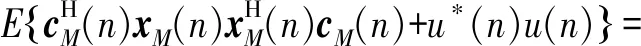
(11)

同理，利用直接平均法，式(11)等價為：

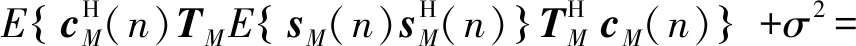
(12)

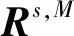
(13)

(14)

式(14)中，λi為相關矩陣Rs,M的特征值，ΛR是由特征值構成的對角矩陣。

由式(6)和式(8)可得：

cM(n)=cM(n-1)-μ(n-1)e*(n-1)ΛMTMsM(n-1)

(15)

將式(15)代入式(13)：

(16)

由式(10)得e(n-1)表達式，代入式(16)：

(17)

(18)

(19)

參考信號服從近高斯分布，則有：

(20)

與文獻[21]推導類似，均方誤差與遞推次數(shù)、參考信號和互擾強度之間的關系為：

(21)

其中，Φ(n)和ψ(l)如式(22)和式(23)所示：

(22)

(23)

由式(21)至式(23)可知，該對消方法收斂的條件是，對于任意的n和i均有|1-μ(n)λi/(Ps+δ)|<1，即步長因子最大值μmax和最小值μmin需滿足：

(24)

式(24)中，λmax=max(λi|i=1,…,M)為特征值的最大值。可見，步長因子的取值范圍由參考信號自相關矩陣特征值及估計的功率值決定。

3.2 MICR分析

參考文獻[21]對收斂狀態(tài)的均方誤差推導，令E{|e()|2}表示該方法在n足夠大時的均方誤差，有：

(25)

由式(25)即可得到基于IVSSTLMS算法的最終互擾對消比MICR，設接收的基帶互擾信號強度為PI，則最終的MICR為：

MICR

(26)

可見，當參考信號一定，互擾信道穩(wěn)定時，基于IVSSTLMS算法的數(shù)字域干擾對消方法的最終MICR僅與步長因子最小值相關，與文獻[21]所得結論一致，但式(8)引入對角矩陣ΛM解決特征值發(fā)散，一定程度上加快了收斂的速度。關于迭代變步長對TLMS算法收斂速度提升的分析可參考文獻[21]，本文不再詳述。

3.3 計算復雜度

除算法收斂速度和穩(wěn)態(tài)MICR外，計算復雜度也是影響應用的重要因素。所以，分析IVSSTLMS算法計算復雜度，并與RLS算法、文獻[23]的VSSNLMS算法和基于LS信道估計對消方法進行對比。假設算法遞推估計變量的維數(shù)為M，步長因子計算的指數(shù)運算一般采用查表法，可暫不考慮其運算量。對于LS信道估計對消方法，設參考信號矩陣為M×M維，且設每間隔L個信號數(shù)據(jù)進行一次估計，則IVSSTLMS算法、RLS算法和LS估計法，輸出NL個期望信號數(shù)據(jù)所需的加、乘和除法次數(shù)如表1所示。可見，IVSSTLMS算法計算復雜度略高于文獻[23]的方法，但遠低于RLS算法和LS估計法。

表1 不同方法所需的計算復雜度

3.4 仿真驗證

本節(jié)將對IVSSTLMS數(shù)字域互擾對消方法進行仿真，并同基于文獻[23]VSSNLMS算法和RLS算法的對消方法進行對比。數(shù)字域干擾對消所處理的為基帶信號，因接收設備目的是有效接收期望信號，所以數(shù)字域的期望信號為零頻，而進入接收設備的數(shù)字域基帶互擾信號因收發(fā)頻率的不同，通常具有一定的頻偏，如圖3所示。仿真以超短波戰(zhàn)術電臺和軍事衛(wèi)星通信常用的QPSK調制為例，信號帶寬為500 kHz，基帶信號為8倍采樣，即采樣率fs=8×500 kHz=4 MHz。收發(fā)頻率間隔250 kHz，設共址收發(fā)設備間的互擾信道為慢衰落多徑信道(因收發(fā)天線相對位置不變，故不考慮多普勒頻移)，傳播路徑數(shù)為4，包括1條直射徑和3條多徑，對應路徑延時和損耗分別為：[10 17 28 55]ns，[34 38 42 51]dB。設接收的期望信號功率為-85 dBm，帶內噪聲強度為-105 dBm，發(fā)送設備輻射功率為37 dBm，射頻域干擾對消的互擾抑制能力為53 dB，進入接收電臺數(shù)字域的互擾信號的ACPR約為30 dB，接收的混合基帶信號頻譜如圖3所示。為便于表示算法的收斂速度，根據(jù)基帶信號采樣率fs，將對消比MICR收斂所對應的迭代次數(shù)n等價轉換為時間t。

圖3 基帶接收信號功率譜示意圖Fig.3 Baseband receive signal power spectrum diagram

基于上述條件，仿真的實現(xiàn)流程如圖4所示。互擾信道響應hM階數(shù)未知，由先驗條件設定階數(shù)M′=31。設信號s(n)和r(n)功率已歸一化，同時為避免步長因子過大和自相關矩陣特征值擴散導致的算法發(fā)散，令IVSSTLMS算法μmax=0.1，文獻[23]的VSSNLMS算法步長因子最大值為1，其余參數(shù)設置如表2所示。

圖4 數(shù)字域線性互擾對消仿真流程圖Fig.4 Digital linear mutual-interference cancellation simulation flow chart

算法參數(shù)參數(shù)取值(1)參數(shù)取值(2)IVSSTLMSκ,μmin20, 0.000 110, 0.001RLSλ0.990.9VSSNLMSα,βμmin0.995,800.0050.99,300.05

統(tǒng)計平均200次獨立仿真結果，得參數(shù)(1)和(2)對應三種方法的MICR∞值，如表3所示，兩種參數(shù)的MICR收斂曲線分別如圖5和圖6所示。

表3 兩種參數(shù)對應的MICR仿真結果

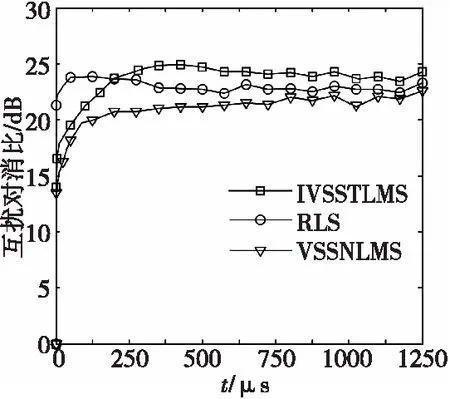
圖5 參數(shù)(1)對應的三種對消方法MICR收斂曲線Fig.5 MICR curves of three cancellation methods for the parameter (1)

由表3和圖5可見，對于參數(shù)(1)，基于IVSSTLMS算法的數(shù)字域互擾對消方法的收斂速度略微慢于基于RLS算法的對消方法，MICR達到20 dB所需收斂時間約為60 μs，但本文方法最終能夠達到的MICR∞比RLS算法提高約1.2 dB。與文獻[23]的VSSNLMS對消法相比，MICR達到20 dB所需收斂時間縮短了50 μs以上，同時最終的MICR∞提高約2.5 dB。由表3和圖6可見，對于參數(shù)(2)，本文方法和RLS算法收斂速度無明顯變化，而VSSNLMS算法MICR達到20 dB所需的時間增至了250 μs左右。同時，本文方法能夠達到的MICR∞分別比RLS算法和IVSSNLMS算法提高了約4 dB和0.9 dB。兩種參數(shù)的仿真結果反映出，本節(jié)IVSSTLMS對消法既具有快的收斂速度，又能夠獲得高的MICR和較低的計算復雜度，與現(xiàn)有對消方法相比，性能得到顯著提升，能夠較好地解決共址無線收發(fā)設備間互擾的數(shù)字域抑制問題。

4 結論

本文提出了基于IVSSTLMS算法的數(shù)字域共址無線收發(fā)設備互擾對消方法，該方法將迭代變步長與變換域LMS算法相結合，具有低的復雜度，在抑制參考信號相關矩陣特征值發(fā)散的基礎上，有效解決了收斂速度與MICR相互制約的問題。仿真結果表明，本文方法的收斂速度和最終獲得的MICR顯著優(yōu)于現(xiàn)有變步長LMS算法和RLS算法，能夠有效實現(xiàn)數(shù)字域互擾對消，為解決共址無線收發(fā)設備間互擾問題提供了有效解決途徑。