貝葉斯框架下基于凸優化的系統偏差估計方法

周 林，劉先省，方擁軍，金 勇

(河南大學計算機與信息工程學院，河南 開封 475004)

0 引言

多傳感器協同探測系統中，融合中心為了獲得被跟蹤目標的“統一”信息(包括時間和空間上的“統一”)，必須首先要在各分布平臺上修正傳感器量測，即消除不“統一”的多傳感器量測誤差。量測誤差主要包含兩類：隨機誤差和系統偏差。前者可以通過濾波等方法消除，而后者則需利用配準方法來改善[1]。系統偏差配準的目的是對傳感器量測(諸如，雷達徑向距和方位角測量、時鐘誤差、傳感器位置等)偏差進行估計和補償，以提高目標定位和跟蹤精確性。

傳統上，研究系統偏差配準問題時通常假設系統偏差先驗信息已知，即系統偏差在整個探測周期是某一未知固定值或呈現緩慢動態演變，此時可利用最小二乘法、最大似然法、加權最小方差法、智能法、信息法、濾波等進行解決[2-7]。但由于探測區域氣候、地形及照射光線各異、外來人為干擾增多、系統非線性和多模型等問題，導致系統機動以及系統偏差演化都難以建模，呈現隨機性、突發性等特性。傳統系統偏差估計方法不再適用解決隨機性的系統偏差配準問題。因此，考慮充分利用序貫量測信息，進而準確、實時估計隨機性系統偏差就尤為重要。

在利用多傳感器序貫量測信息，通過構造目標函數，進而解決系統偏差估計的時候，無論目標函數中的參數有無約束條件，擬牛頓法、共軛梯度法、可行方向法等典型策略都取得了較好效果[8-10]。但上述方法通常找到的是平穩點或駐點(即局部最優點)，甚至找不到局部解，進而也較難找到所有極小點集合中的最好點(即全局最優點)。盡管全局最優算法的設計非必需，但它有助于解決優化問題，常見的優化算法包括遺傳法、粒子群法、蟻群法、區間方法等[11-14]，它們具有全局最優性和良好的約束條件適應性，但實時性差、較難獲得易驗證的全局最優性條件。因此，考慮引入凸優化方法來求解全局最優解，該方法時間復雜度小，可用于可靠和迅速地優化模型求解。

研究發現Metropolis-Hastings(簡稱M-H)算法是一種近似貝葉斯方法[15-16]，屬于有約束的后驗概率最大問題，新樣本的選擇誤差會不斷增加，從而導致魯棒性得不到保證。因此，本文以文獻[16]中的系統偏差最大似然函數為基礎，構造系統偏差估計的拉格朗日乘子二次函數并討論構造函數的凸性，進而提出基于凸優化的系統偏差估計方法。

1 問題的描述

正如前面所述，當復雜環境或未知因素等出現時，導致系統以及系統偏差動態模型難以構建,傳統方法不再適用。假設某一傳感器探測系統中，考慮兩個問題：1)機動目標的狀態難以建模；2)考慮傳感器量測受外界隨機干擾。因此，可只對極坐標系下系統的非線性量測建模：

(1)

為討論方便，將每個傳感器極坐標系下量測模型轉換為笛卡兒坐標系下，其模型如下：

(2)

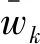
由于機動目標狀態模型未知，若想獲取估計系統偏差和目標狀態信息，可利用zk={zk(i);i=1,…,n}及似然函數最大化方法估計傳感器系統偏差bk和目標狀態xk，即：

(3)

對n部傳感器，假設量測具有白噪聲，進而可得量測似然函數：

(4)

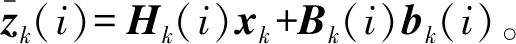
(5)

式(5)中,K2是常數K1的對數。忽略不相關常數項，通過優化得出目標最大似然估計：

清代乾隆年代[12]，江河商運發展，博羅老城、惠東梁化、惠陽的淡水、多祝又逐漸成為惠州區域主要的商業圩鎮，陸續發展興盛。宋、清惠州兩次人口的暴增[13]，導致當地民間信仰祭祀場所對應惠州人口的聚居點而增加，羅浮山道教也兩次借機復興。同時，惠州地貌的特征使得臺地、丘陵、平原階地沿東江相間分布，造就治水民間信仰隨人口聚居沿東江分布。

(6)

利用貝葉斯估計理論，得出多目標最大似然估計函數如下[16]：

(7)

2 基于凸優化的系統偏差估計方法

2.1 拉格朗日乘子二次函數

凸優化模型可對一般非線性優化模型進行局部逼近，是研究非線性規劃問題的主要途徑。本節將式(7)的系統偏差的最大似然估計函數轉化為具有目標函數、約束函數的優化問題，其中目標函數核心是構造拉格朗日乘子二次函數形式，約束函數既包含求解參數空間邊界不等式約束條件也包含量測差形式的等式約束條件。同時，對上述優化問題的凸性進行判斷分析。

解優化問題用到的目標函數和約束函數即使是光滑的，有時候仍很難求解。為了更好描述后驗概率函數并用優化函數條更精確估計參數，目標函數和約束函數之間的數學關系通過表達式描述，即用拉格朗日乘子二次函數表示，以第i個傳感器為例，其拉格朗日乘子二次函數為：

(8)

式(8)中，L表示系統偏差拉格朗日二次函數；γ表示包含待估系統偏差的表達式；λ1、λ2、λ3分別表示約束條件系數，它們根據實際問題取值；f1、f2、f3分別表示約束條件。

傳統求解拉格朗日乘子二次函數最優解的方法是用二次函數對待求參數求偏導并令偏導表達式等于零，進而得到解析解。盡管該方法易于數學描述，但弊端是當目標函數非凸(或非凹)時，函數局部極值的存在會導致函數全局最優解得不到確保。由于凸優化模型是研究非線性規劃問題的主要途徑，因此，可對上述拉格朗日乘子二次函數進行凸性判斷。若函數呈現凸性，則其最優解可利用凸優化技術直接求解；若函數呈現非凸性，則可利用約束條件松弛、對偶等措施將非凸問題轉換為凸問題之后再求解。

2.2 二次函數的凸性判斷

判斷函數凸性的充要條件是函數的Hessian矩陣為半正定陣。求拉格朗日乘子二次函數L(γ,λ1,λ2,λ3)對系統偏差bk的Hessian矩陣，并將前述的A、γ等代入，可得如下Hessian矩陣表達式：

(9)

上述已用凸優化方法證明拉格朗日乘子二次函數的凸性，結合拉格朗日乘子方法求解目標函數，可將拉格朗日乘子二次函數最優化問題等價為有約束的凸優化問題，具體表達式如下：

(10)

L(γ,λ1,λ2,λ3)=

(11)

因此，根據拉格朗日乘子二次函數表達式，本文通過Matlab軟件附帶的專業凸優化工具包來獲得每一個采樣時刻k使L最小的系統偏差bk。

2.3 算法描述

已有研究中，推導出的系統偏差最大似然估計函數，可利用M-H方法進行尋優求解，從而穩態模擬參數貝葉斯估計方法[16]，但該方法存在兩個問題：1)本質上是一種迭代采樣方法，馬爾科夫鏈的鏈長影響算法的實時性。2)通常較易找到局部最優點而非全局最優解。因此，為了提高估計實時性和全局最優性，本文提出基于凸優化的系統偏差估計方法，其流程如下圖1所示。

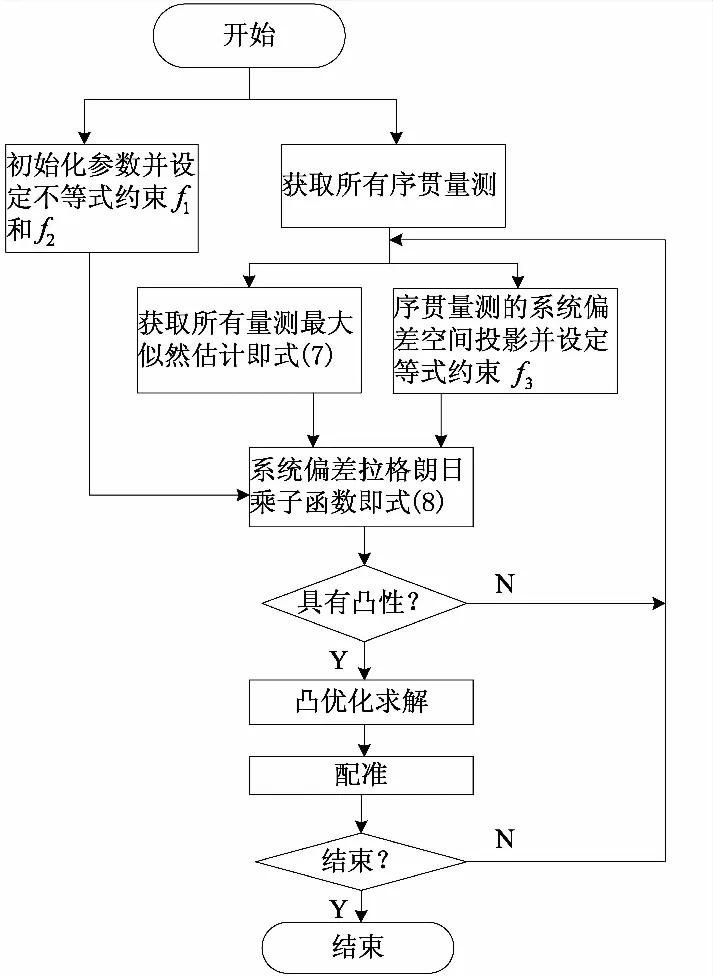
圖1 算法流程圖Fig.1 The flowchart of algorithm

3 仿真結果與分析

為了驗證所提算法可行性和有效性，仿真假設用配置在異地的兩部傳感器探測和跟蹤機動目標，且機動目標在2D坐標系統中的運動模型如下：

同時，兩部傳感器都設定為二維極坐標量測方式，即量測包含徑向距和方位角，其量測模型如下：

zk(i)=hi(xk)+bk(i)+wk(i)i=1,2

(12)

式(12)中，傳感器量測zk(i)=[ρk(i)θk(i)]T；量測噪聲分別為σρ(1)=150 m，σθ(1)=0.5°；σρ(2)=80 m，σθ(2)=1°，非線性測量函數hi(·)如下：

(13)

式(13)中,i=1,2, 且(ζi,ηi)為笛卡兒坐標系下傳感器位置， (ζ1,η1)=(300 km,-200 km)，(ζ2,η2)=(80 km,75 km)。

假設系統偏差bk具有隨機性(即動態演化模型未知)，其估計初始b0=[0 0 0 0]T。為了驗證所提算法的可行性和有效性，將本文算法與先前研究的M-H算法和ML算法進行比較。為了描述系統偏差的隨機性，本文凸優化算法的待估系統偏差的在徑向距、方位角和俯仰角范圍rrange(i)、θrange(i)的上限和下限分別取整個仿真周期系統偏差模型的最大值和最小值，使之體現參數空間的廣域性和可行性。為了與M-H算法進行比較，設置的相關參數為：閾值δ=0.4，Markov鏈長L=1 000，舍去預迭代值的個數為m=200；仿真采樣100次；Monte Carlo次數為50次。算法運行硬件條件為Intel Core i7-2600 CPU 4 GHz。

3.1 參數估計性能仿真

圖2為傳感器A和傳感器B在徑向距和方位角上隨機性系統偏差真實值且有突變發生。為了說明算法的有效性和可行性，圖3和圖4給出一次仿真得出的三種算法和真實系統偏差比較關系曲線圖。由于隨機性系統偏差難以建模，考慮充分利用傳感器序貫量測的最大似然方法(簡稱ML)、Metropolis-Hasting(簡稱M-H)及本文提出的凸優化方法(簡稱Convex)進行對比。從圖3和圖4可以看出，相比于其他兩種方法，Convex方法在徑向距系統偏差估計效果較好；在方位角系統偏差估計效果，Convex方法要優于M-H方法且能估計出突變量，但是要遜于ML方法。原因在于系統偏差具有隨機性和突變性，M-H和Convex兩種方法在采樣、學習過程中隨機時變地在參數空間內游走，導致噪聲存在時變方差，而ML方法的噪聲滿足某一近乎恒定方差，這在需要分辨率較高的方位角仿真圖中能得到驗證。

圖5和圖6為經過50次Monte Carlo仿真后三種算法關于傳感器A和傳感器B關于徑向距、方位角的均方根誤差比較圖。從圖5和圖6可以看出，Convex方法在傳感器A和B徑向距的RMSE要好于M-H方法和ML方法；但傳感器A和B方位角的RMSE，Convex方法基本上處于M-H方法和ML方法之間，分析可知Convex方法在方位角估計精度并沒有定性于一定比M-H方法或ML方法中的任一種方法好。

圖2 傳感器A和B的系統偏差Fig.2 Systematic biases of the sensor A and B

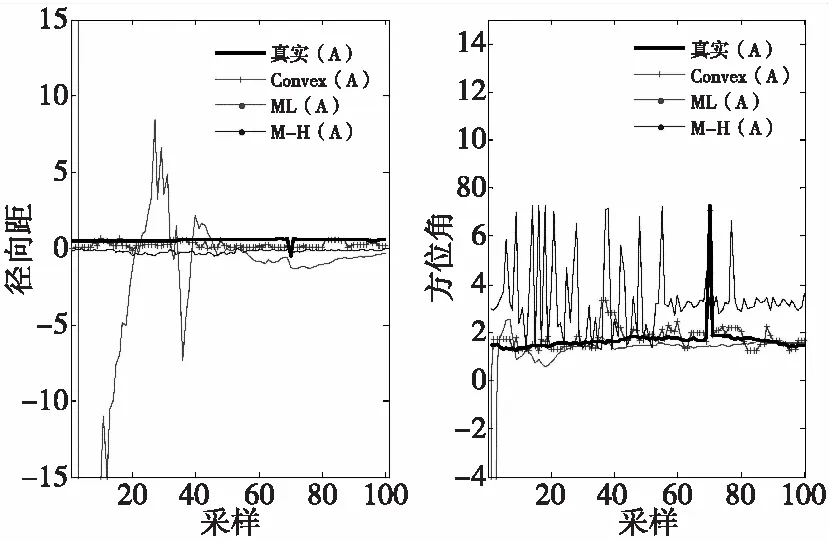
圖3 傳感器A的系統偏差估計比較圖 Fig.3 Comparison of systematic bias estimation on sensor A

圖4 傳感器B的系統偏差估計比較圖Fig.4 Comparison of systematic bias estimation on sensor B

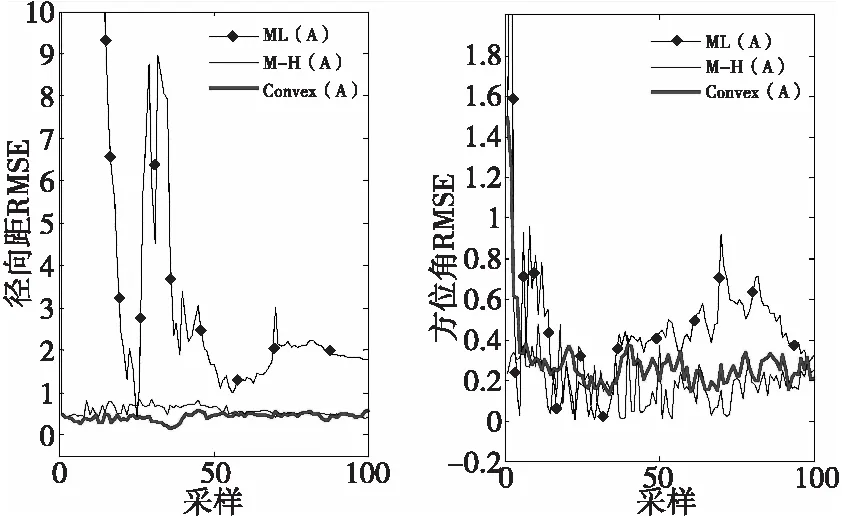
圖5 傳感器A的RMSE比較圖Fig.5 Comparison of RMSE on sensor A

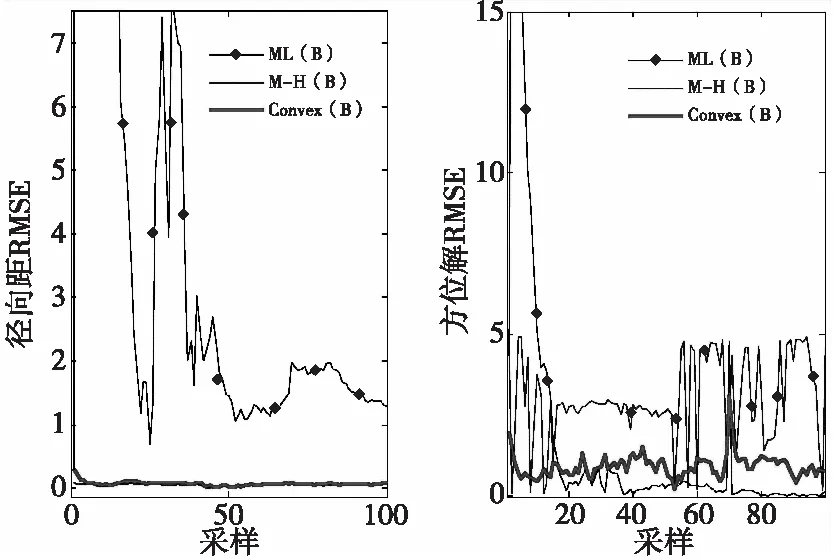
圖6 傳感器B的RMSE比較圖Fig.6 Comparison of RMSE on sensor B

為了更直觀地描述整個仿真過程的估計性能，表1給出經50次Monte Carlo仿真后三種算法估計出的傳感器A和B在徑向距和方位角系統偏差的平均均方誤差。

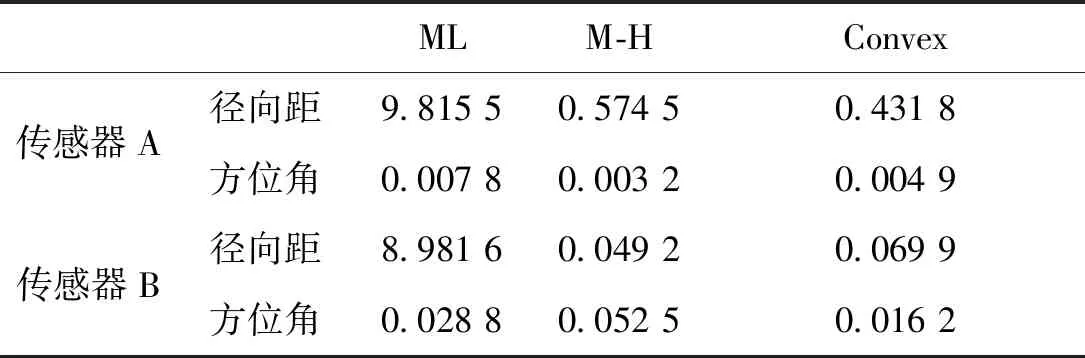
表1 三種算法的平均均方根誤差

3.2 復雜度分析

為了驗證Convex方法的實時性，經50次Monte Carlo仿真可知，三種算法的平均時間復雜度如表2所示。

分析原因，可依據ML、M-H及Convex算法的時間復雜度計算，其分別為O(n2·k)，O(L·n)，O(max{n3,n2·m,F})(其中，n表示系統狀態維數，k表示第k次采樣，L表示Markov鏈長，m表示約束不等式約束條件數目，F表示對所有不等式約束條件及其一階、二階導的計算代價)[17]。

表2 估計方法的平均運行時間

綜合仿真曲線圖和數據可知，在參數空間尋優求解范疇，Convex方法整體上比M-H方法耗時少、精度高；在整個仿真采樣時間段的估計精度范疇，Convex方法比ML方法精度高。

4 結論

在貝葉斯估計框架下，本文充分利用多傳感器的序貫量測信息，首先從量測最大似然函數入手，推算得到與狀態參數無關的多傳感器量測最大似然函數；然后將機動目標的系統模型從狀態空間投影到系統偏差空間，并將投影表達式作為系統偏差二次函數的等式約束條件；隨后，將待估的參數空間范圍作為不等式約束條件，并聯合等式約束條件，將最大似然估計問題轉化為具有目標函數、約束函數的凸優化問題；最后利用凸優化工具包實現多傳感器系統偏差的優化求解。本文新方法解決了當隨機性的系統偏差難以建模時，傳統估計方法帶來的非全局最優解、非實時性等問題。