密集雜波下的模糊數據關聯多目標跟蹤算法

康旭超，何廣軍，陳 峰，何其芳

(空軍工程大學防空反導學院，陜西 西安 710051)

0 引言

密集雜波環境下的多目標跟蹤一直是目標跟蹤領域的一個難題,雷達捕捉到的信號除了真實量測外還包括雜波引起的虛假量測，難以實現對目標的準確跟蹤[1]。很多學者對于虛假目標與目標的區分已經做了很多研究，但都存在計算量大、區分目標復雜的問題，不利于目標的實時跟蹤[2]。

在雜波環境下對目標進行跟蹤的概率數據關聯算法(PDA)計算量小，但在雜波密集的超低空環境下容易跟錯目標。聯合概率數據關聯算法(JPDA)能夠解決雜波密集環境下的目標跟蹤，但隨著目標數量的增加，算法計算量過大，不利于目標的實時跟蹤[3]。文獻[4]通過模糊聚類得到每個測量點跡與目標預測位置之間的隸屬度,并將其作為權值系數對有效回波的信息量進行加權,來實現目標的狀態估計的更新，提高了跟蹤的實時性，但密集雜波環境下多目標跟蹤的準確性不佳。文獻[5]在考慮到存在的公共量測對目標估計的影響，在模糊聚類的基礎上加入了尺度因子，并根據目標群的位置信息以及運動方向信息進行多級聚類，一定程度上提高了目標跟蹤的準確性，但并未考慮多目標在近距離和遠距離情況下公共量測對于目標估計的影響權重的不同，影響跟蹤精度。本文針對此問題，提出了密集雜波下的模糊數據關聯多目標跟蹤算法。

1 密集雜波下的多目標跟蹤問題

1.1 問題描述

假設在多目標跟蹤系統中，有C個跟蹤目標，在k時刻目標i(1,2,3，…，M)的運動狀態方程為：

(1)

假設k時刻目標i的觀測方程為：

(2)

本文解決的問題是在某時刻k測得n個觀測量Zk(j)(j=1,2，…，n)，觀測量中包含密集雜波(虛假目標)，在無法區分雜波與真實目標量測的前提下，利用模糊聚類的思想對每個觀測量(包含雜波)進行聚類[6]，得到每個觀測量相對于目標的隸屬度作為模糊關聯概率，分析遠近距離兩種情況下公共量測對目標的影響，引入影響因子重建模糊關聯概率矩陣，然后結合卡爾曼濾波的方法對不同觀測量的狀態估計進行加權融合得到下一時刻目標的估計狀態，通過對目標軌跡進行單獨的估計從而實現對超低空多目標的實時跟蹤。

1.2 模糊C均值聚類

模糊劃分矩陣U=(μij)c×n，定義模糊函數：

(3)

式(3)中，dij為樣本j與目標i之間的歐氏距離‖zj-vi‖，vi表示目標i的聚類中心，m表示模糊指數，滿足1≤m≤。

利用最小化目標函數完成模糊分類，具體流程如下：

1) 確定目標C，以下一時刻狀態預測值作為初始聚類中心，選擇合適的模糊指數m，從聚類有效性試驗研究中得到m的最佳取值范圍為[1.5 2.5]，通常取m=2，給定迭代停止閾值ε。

2) 初始化隸屬度矩陣U，計算各個數據到聚類中心的距離dij，計算隸屬度矩陣，t=0。

3) 更新隸屬函數矩陣U=(μij)c×n。

其中，

(4)

4) 更新聚類中心

(5)

5) 若|vi(t)-vi(t+1)|<ε，迭代結束，得到模糊劃分矩陣，否則轉到步驟3)。

本文中，在目標數(聚類數)已知的前提下，以下一時刻目標的預測位置為聚類中心，以各量測與聚類中心的歐氏距離為測度計算量測對于目標的隸屬度。

2 密集雜波下的模糊數據關聯多目標跟蹤算法

2.1 模糊數據關聯方法

建立目標橢圓跟蹤門，確認各目標有效觀測距離ri，‖ri‖≤τi減少野值。其中τi為目標i的觀測閾值。

1) 建立量測歸屬矩陣Λ：

(6)

式(6)中，

(7)

?11=1表示觀測量z1落入目標1的跟蹤門，?23=0表示觀測量z3沒有落入目標2的跟蹤門。

圖1中▲表示目標的預測位置，以目標預測位置為中心建立跟蹤門，●表示某一時刻量測點(包含雜波與真實目標量測)，假設某一時刻，目標只有一個真實量測，其余為雜波引起的虛假量測，跟蹤門重疊區域的量測為公共量測。

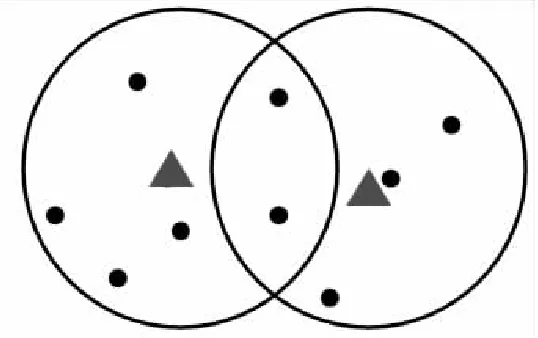
圖1 目標確認區域的量測值分布Fig.1 Distribution of measurements in target recognition area

傳統算法中大多未考慮多目標跟蹤門出現重合，即存在公共量測的情況[4]。雖然有學者考慮到存在公共量測時公共量測對目標估計的影響，但未考慮多目標在距離較近和較遠的情況下公共量測對于目標估計影響權重的變化，影響跟蹤的精確性[11]。改進的模糊聚類關聯算法通過對多目標遠近距離下公共量測對于目標估計的影響權重的不同進行了分析，在遠近兩種情況下實時調整公共量測的權重。

對于兩個相距較遠的目標，認為公共量測區域量測值為目標真實觀測的概率很小，通常認其為雜波，此時引入尺度因子來降低公共量測對于目標估計的權重。但兩個目標相距較近時，尤其是進行交叉時，非公共量測為雜波的可能性更大，此時應該引入尺度因子降低非公共量測的權重。

當目標距離較遠時量測分布如圖2所示。

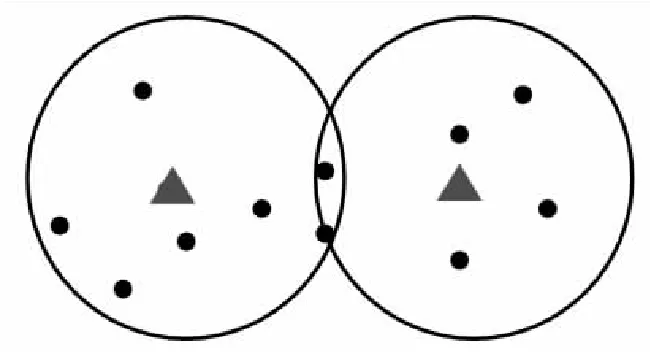
圖2 目標相距較遠時量測分布Fig.2 Distribution of measurements when targets are far apart

此時公共量測與目標預測的偏差較大，為雜波的可能性較高，引入影響因子降低公共量測的權重。

當目標距離較近時量測分布如圖3所示。

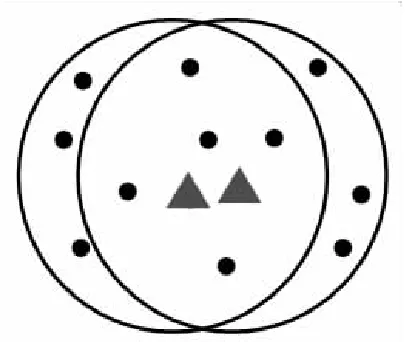
圖3 目標相距較近時量測分布Fig.3 Measurement distribution when the target is close to each other

此時非公共量測與目標預測的偏差較大，為雜波的可能性較高，引入影響因子降低非公共量測的權重。

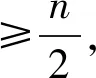
(8)

引入影響因子ζpub降低公共量測的權重

(9)

?ij*=ζpub?ij

(10)

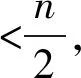
非公共量測集合

(11)

引入影響因子ζnonpub降低非公共量測的權重

(12)

?ij*=ζnonpub?ij

(13)

引入影響因子后的量測分布矩陣：

(14)

2) 建立量測權值矩陣Π

(15)

式(15)中，ωij=?ij*μij。

2.2 結合模糊聚類關聯的多目標跟蹤算法

利用FCM算法得到量測權值矩陣U，結合卡爾曼濾波，針對雜波環境下量測的不確定性利用聯合關聯信息對目標進行單獨的跟蹤。其具體流程如下：

步驟2 預測下一時刻目標狀態，作為下一時刻的聚類中心。

(16)

步驟3 觀測預測。

(17)

步驟4 確定各目標的有效觀測，最大觀測范圍ri，建立量測歸屬矩陣Λ。

步驟5 利用模糊聚類計算各量z(j)測屬于目標i的隸屬度關系矩陣U=(μij)c×n。

步驟6 根據公共量測數與總量測數的關系引入尺度因子ζpub，ζnonpub，建立量測權值矩陣Π。

步驟7 一步預測均方誤差。

Pi(k/k-1)=Fi(k/k-1)Pi(k-1)·
Fi(k/k-1)T+Qi(k-1)

(18)

步驟8 計算濾波增益。

Ki(k)=Pi(k/k-1)Hi(k)T(Hi(k)·
Pi(k/k-1)Hi(k)T+Ri(k))-1

(19)

步驟9 利用不同量測相對目標的權值作加權融合，得到第i個目標的狀態更新值。

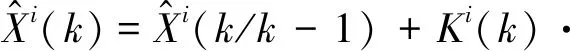
(20)

步驟10 估計均方誤差。

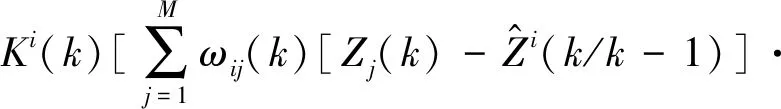
(21)

3 仿真結果與分析

傳統多目標跟蹤算法未考慮公共量測對估計精度的影響[4]，本文算法在此基礎上引入公共量測影響因子，調整公共量測權重，進一步提升密集雜波下多目標跟蹤性能。

分別對2個勻速直線運動的目標建立目標狀態方程：

X(k+1)=FX(k)+Gw(k)

(22)

觀測方程為：

Z(k)=HX(k)+v(k)

(23)

式(23)中，

為了檢驗算法的可靠性，設置了兩個場景：

場景1 檢驗兩個目標距離較遠(不存在交叉)時算法的可靠性。

假設有2個勻速直線運動的目標，目標1、目標2的初始位置分別為(1 500,4 000)，(1 000,900)，目標1水平速度分別為300 m/s，垂直方向上的速度為200 m/s，目標2水平速度分別為200 m/s，垂直方向上的速度為100 m/s，采樣周期為0.2 s，隸屬度矩陣U的指數設為2，最大迭代次數設為100，迭代終止條件隸屬度最小變化量為1×10-5。目標真實運動軌跡如圖4所示。

在雜波較為稀疏的情況下，取雜波系數λ=2時，目標跟蹤軌跡及誤差曲線如圖5、圖6所示。

在雜波較為密集的情況下，取雜波系數λ=5時，目標跟蹤軌跡及誤差曲線如圖7、圖8所示。

圖4 目標真實運動軌跡Fig.4 The real trajectory of the target

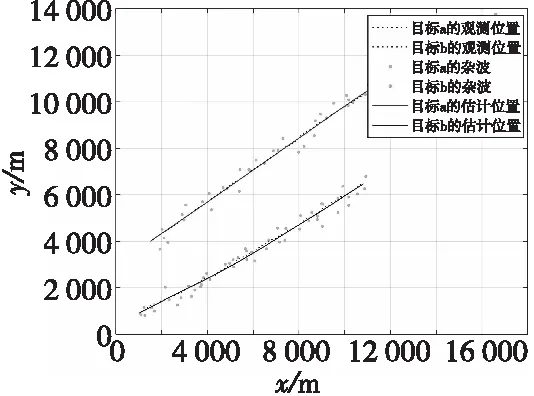
圖5 目標跟蹤軌跡Fig.5 Target tracking trajectory

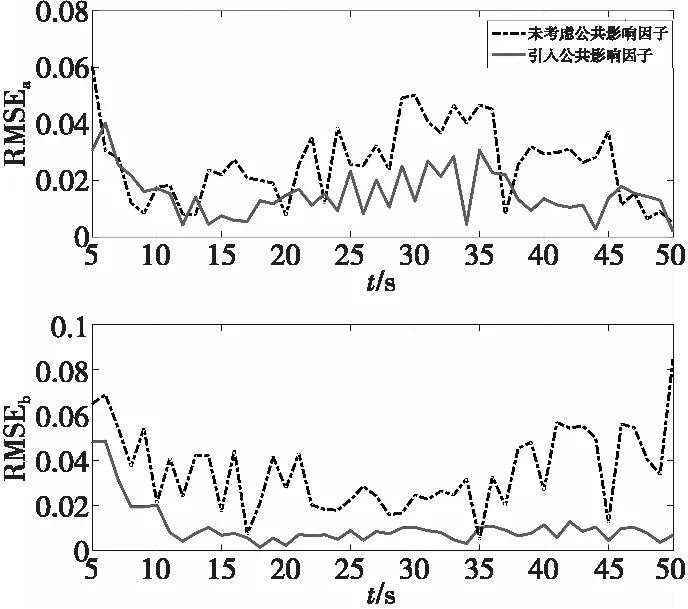
圖6 目標a與b的誤差曲線Fig.6 Error curves of targets a and b

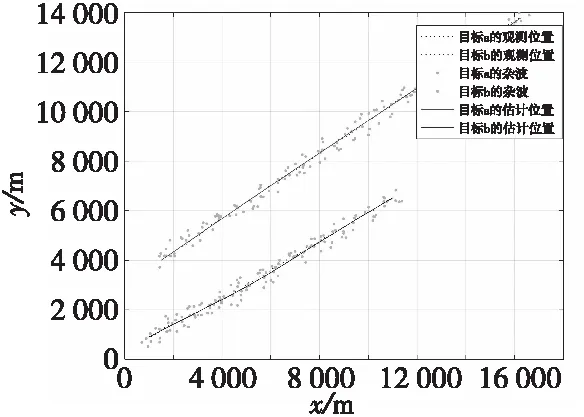
圖7 密集雜波環境下目標跟蹤軌跡Fig.7 Target tracking trajectory in dense clutter environment

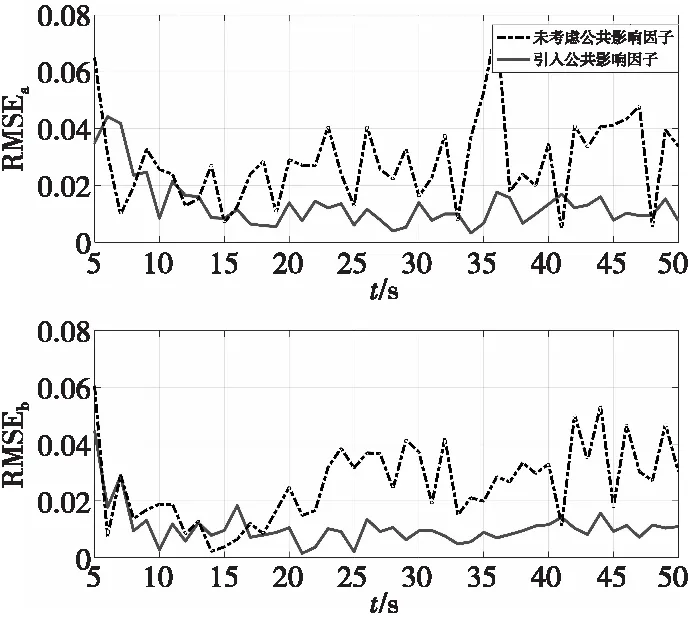
圖8 密集雜波環境下目標a與b的誤差曲線Fig.8 Error curves of target a and b in dense clutter environment

由仿真結果分析可知，當兩目標距離較遠時，對比未考慮公共影響因子的傳統多目標跟蹤算法，本文算法能夠對目標進行更為精確的跟蹤，誤差基本控制在0.05以內。本文算法在傳統算法的基礎上通過對公共量測量的分析調整權重以提高估計精度，但由于在雜波相對較為稀疏的環境下公共量測較少，因此性能提升相對不明顯。本文研究內容為雜波密集環境下多目標跟蹤算法性能的提升，仿真結果證明在雜波密集環境下本文改進算法有較好的跟蹤效果。

場景2 檢驗兩個目標距離較近(存在交叉)時算法的可靠性。

假設有2個勻速直線運動的目標，目標1、目標2的初始位置分別為(1 500,1 000)，(1 000,900)，目標1水平速度分別為300 m/s，垂直方向上的速度為200 m/s，目標2水平速度分別為200 m/s，垂直方向上的速度為100 m/s，采樣周期為0.2 s，隸屬度矩陣U的指數設為2，最大迭代次數設為100，迭代終止條件隸屬度最小變化量為1×10-5。目標真實運動軌跡如圖9所示。

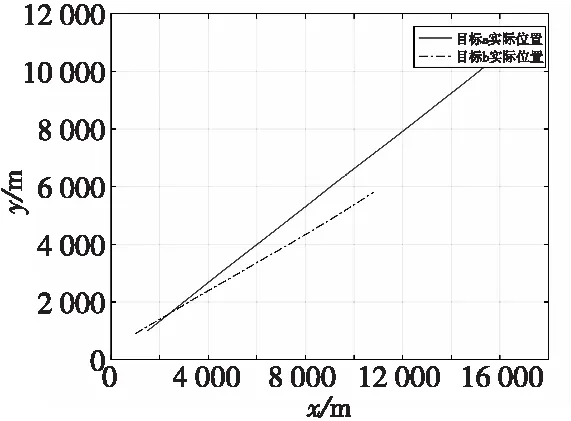
圖9 目標真實運動軌跡Fig.9 Target real motion trajectory

在雜波較為稀疏的情況下，取雜波系數λ=2時，目標跟蹤軌跡及誤差曲線如圖10、圖11所示。

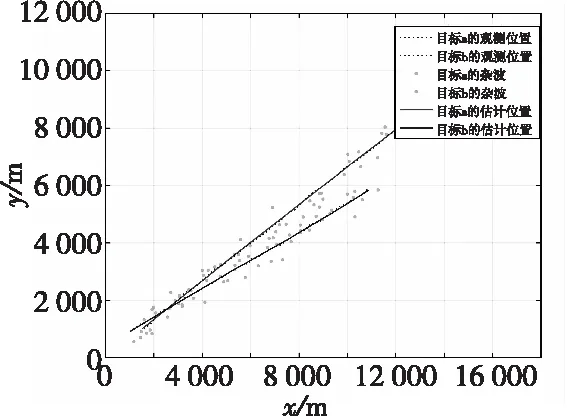
圖10 目標跟蹤軌跡Fig.10 Target tracking trajectory

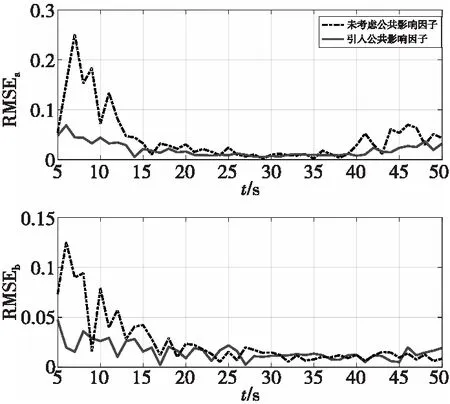
圖11 目標a與b的誤差曲線Fig.11 Error curves of targets a and b

在雜波較為密集的情況下，取λ=5時，目標跟蹤軌跡及誤差曲線如圖12、圖13所示。

由以上仿真結果可知，當兩目標距離較近時，未考慮公共因子的傳統算法有較大的誤差，本文算法通過對公共影響因子權重的調整，使誤差明顯減小，誤差波動也得到了明顯的抑制。在雜波密集的情況下，雜波數增加，該算法依然能夠對多目標穩定跟蹤，誤差控制在0.1之內，基本穩定在0.05附近。

通過對兩種場景的仿真分析可得不論是對于近距離目標還是遠距離目標，相較于未考慮公共影響因子的傳統多目標跟蹤算法，本文改進算法均能更為準確地反映目標的運動軌跡，且對于雜波密集下的多目標跟蹤有較好的跟蹤效果，證明了所提出的跟蹤算法更適合對密集雜波干擾環境下的多目標進行跟蹤。

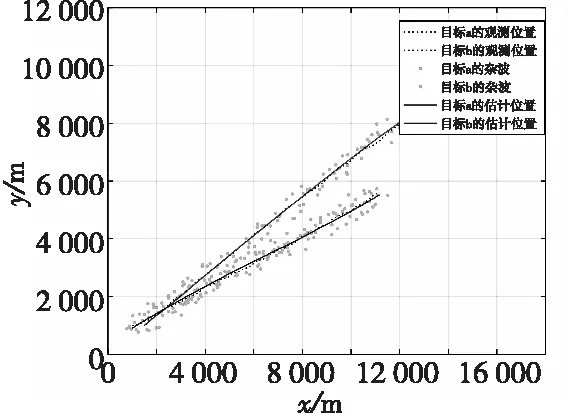
圖12 密集雜波環境下目標跟蹤軌跡Fig.12 Target tracking trajectory in dense clutter environment

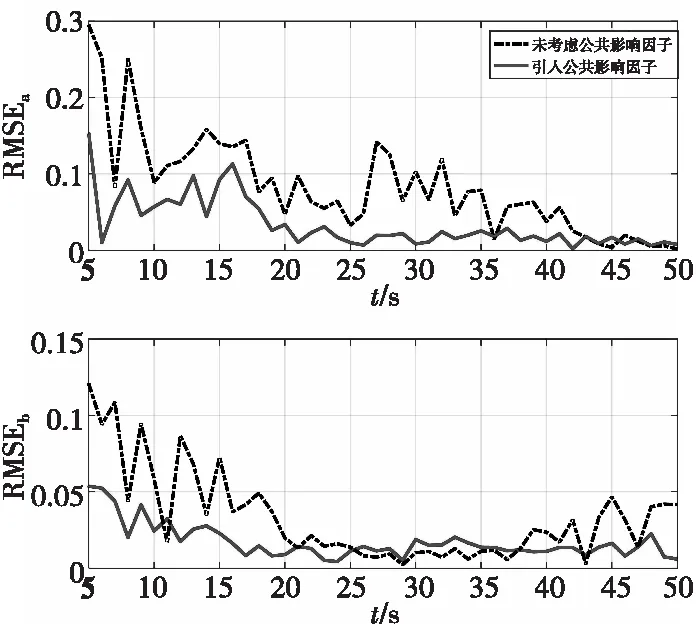
圖13 密集雜波環境下目標a與b的誤差曲線Fig.13 Error curves of target a and b in dense clutter environment

4 結論

本文提出密集雜波下的模糊數據關聯多目標跟蹤算法，該算法利用模糊聚類，得到不同觀測量相對目標的隸屬度作為模糊關聯概率，引入遠近距下的公共觀測影響因子重建模糊關聯概率矩陣，將重建后的模糊關聯概率作為權值，結合卡爾曼濾波對某一時刻不同量測的狀態估計加權融合作為目標的估計狀態，實現目標的狀態更新。仿真結果表明，在雜波密集的環境下，采用本文算法在能夠保證目標跟蹤實時性的同時引入遠近距下公共觀測影響因子對不同觀測量的狀態估計進行加權，保證了目標跟蹤的準確性。