動態矩陣控制在三自由度直升機中應用研究

方力智

摘要：本文主要研究的是動態矩陣控制在三自由度直升機系統中的應用問題，將在基于三軸數字PID控制器的基礎上，對俯仰軸以及旋轉軸進行動態矩陣控制來優化系統的響應。

關鍵詞：三自由度直升機系統;三軸數字PID控制;動態矩陣控制

作為一種可以在部分特性上仿真直升機的控制系統，三自由度模擬飛行姿態系統[1]被眾多控制技術學者關注并研究。它自身的多輸入多輸出特性、強耦合特性和強非線性特性，決定了它是一個控制工程中的難控制對象。本文研究預測控制在三自由度模擬飛行姿態系統中的應用，即將其簡化為一個弱耦合、若非線性的系統，在其上應用預測控制。

1 控制方法

1.1控制方法

控制律的設計主要采用閉環控制。考慮到1、本文所研究的動態矩陣控制需要基于漸近穩定的系統，所以需要對該系統先進行內環調穩;2、另外考慮到本文要將該控制律應用到實際系統當中，將選取容易實現且魯棒性好的PID控制器作為系統內環控制器。在內環系統使用PID控制器調穩之后，再加入外環的動態矩陣控制以優化控制性能。

1.2控制系統結構

原本的系統對于俯仰軸以及滾轉軸依然有著一定的耦合性，通過引入兩個新的控制量 ，把該系統分解成兩個互不相關獨立的控制通道，俯仰運動和偏航運動。而偏航運動由滾轉運動和偏航運動兩個部分組成，滾轉軸的滾轉運動將直接影響到偏航運動。下圖2-1表示整個系統的控制流程，對于主控對象俯仰角及偏航角采用內環PID控制加上外環動態矩陣控制，對于滾轉角則只使用PID控制即可。

2 三自由度數字PID控制律研究

2.1系統模型構建

對系統的三軸使用根據系統的動力學模型，對系統進行SIMULINK建模，所建俯仰軸模型如下圖3-1所示。并基于該模型對它進行PID控制研究。

2.2數字PID控制簡述

在實際電控系統中，用的都是傳感器的采樣數值進行控制，而新的控制量也是基于不同采樣時刻的偏差值計算出來的。所以在這里，需要對該系統進行離散化PID控制，離散化之后的PID控制器表達式為：

其中， 為比例增益， 為采樣周期， 為積分時間， 為微分時間， 為為了更加逼近實際系統的作動過程，對于三軸的連續系統，將使用Simulink進行建模仿真，而對于其控制部分，將使用M函數進行數字PID控制的實現。

2.3 PID參數整定

PID控制器參數整定表示的是確定了控制器為PID形式之后，通過調節 等控制器中的參數，使得控制回路的動態特性及靜態特性能滿足期望的指標，從而達到理想的控制目標。PID控制方法當然也有著自己的局限性和缺陷。它控制的模型必須保證系統參數不會隨著時間變化。并且，PID參數整定出來的算法，每一次整定出來的解都只不過是局部優化解，并不是全局最優值。所以，只需要找到局部最優解，使它滿足指標要求即可。本次研究使用的PID參數整定方法為擴充臨界比例度法[2]：首先選擇一個足夠短的采樣周期 ;在仿真運行的時候，只使用比例系數 ，用一開始選定的采樣周期 ，慢慢增大比例系數 的數值，直到系統出現等幅度震蕩的時候，記錄下當前 值，當前的臨界震蕩周期也記錄下來;根據齊格勒-尼克爾斯提供給的經驗公式，計算得到不同類型的控制器的控制參數。

2.4 數字PID仿真結果

在用臨界比例度法調節完三個軸上的PID的時候，曲線的線型已經十分接近想要的結果，但是結果并不能直接達到滿意的效果。于是考慮在已有的PID情況下進行微調。微調則是參考經驗試湊法[3]進行即可。一般情況下，增大比例系數 能夠減小偏差，并同時減弱系統中負載的擾動效果，但同時它會加強測量噪聲對系統的影響，而當 增幅過大時，它極有可能使系統變成不穩定系統;積分控制器調控的是過去的偏差量，其主要作用是消除系統中的靜差，減小 會增大系統超調，但是增大它又會導致系統的穩定時間下降，需根據實際情況慢慢調試;微分控制器是對過去偏差的差值進行調控，換句話說，就是對誤差的變化率進行調控，有一定的預測功能，增大 值能加快系統的響應時間，但是如若 過大，會讓控制對象變成不穩定系統。

最終對于仿真模型調整的三軸PID參數如下表3-1所示。其中俯仰軸的過沖17.11%。系統穩定到設定值2%偏差的時間為0.355s;橫側軸的峰值振幅為1.0743，過沖7.43%。系統穩定到設定值2%偏差的時間為0.160s;旋轉軸和橫側軸有著很大的耦合關系，需要建立在橫側軸PID整定調穩之后，進行旋轉軸PID調節;旋轉軸的峰值振幅為1.2791，過沖27.91%。系統穩定到設定值2%偏差的時間為1.025s。

3 動態矩陣控制律研究

3.1DMC控制簡述

動態矩陣控制是一種計算機控制技術，它一般情況下多用于穩定系統，對于不穩定系統，則可以加入內環控制器將其先調節到穩定或者漸近穩定的情況下再進行基于系統的單位階躍響應的控制器設計。動態舉著控制的控制結構主要由預測模型、滾動優化、誤差校正和閉環控制形式構成[4-7]。

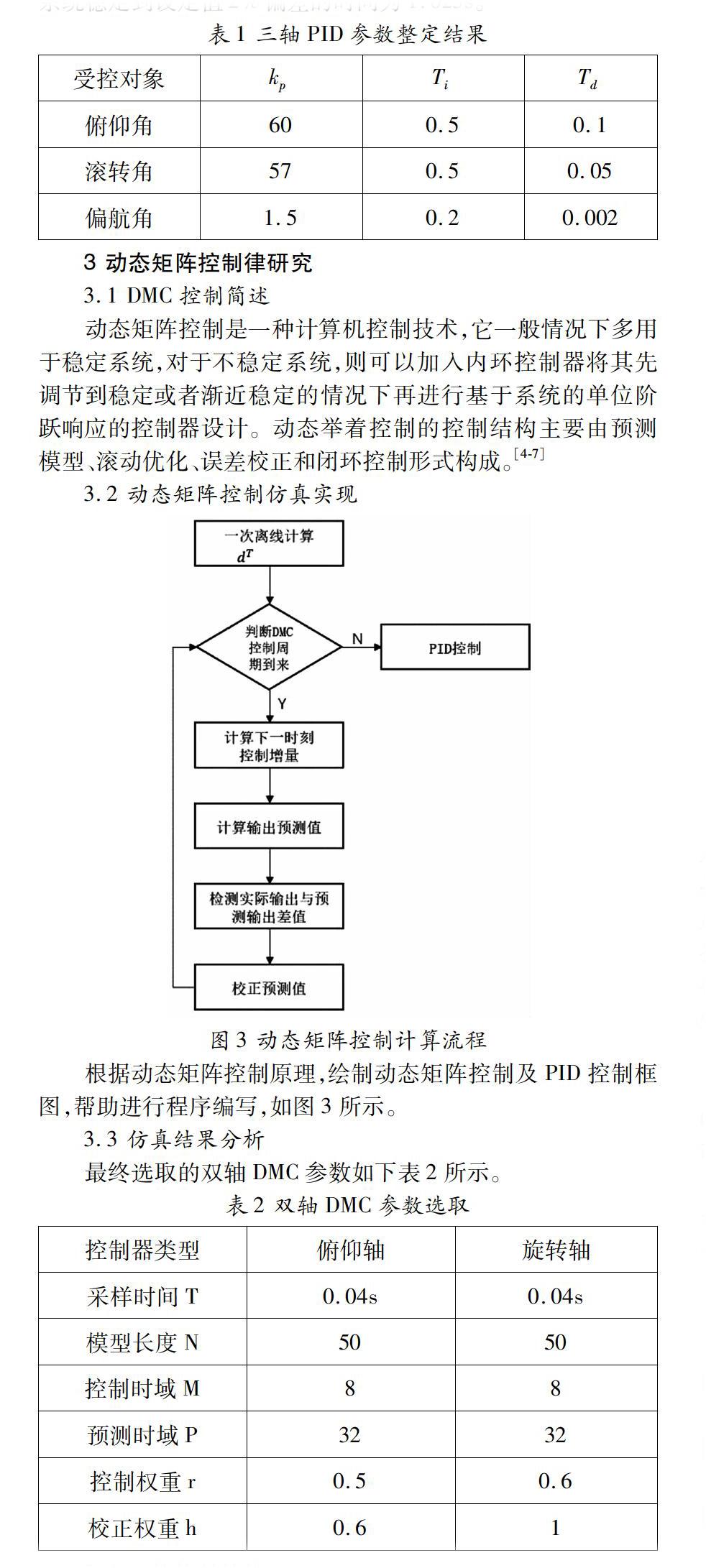
3.2動態矩陣控制仿真實現

根據動態矩陣控制原理，繪制動態矩陣控制及PID控制框圖，幫助進行程序編寫，如圖4-1所示。

3.3仿真結果分析

最終選取的雙軸DMC參數如下表4-1所示。

3.4雙軸控制性能

使用MATLAB進行控制器設計及仿真實驗。下圖4-2中，（a）圖和（b）圖為最終用DMC改進之后的俯仰軸及旋轉軸控制效果，可以看出加入了DMC控制的系統快速性和穩定性都相對于只使用PID控制器的系統更加良好。

（a）俯仰角

（b）偏航角

4 結論

本文針對三自由度直升機簡化后的弱耦合、弱非線性模型進行了預測控制器的設計，在內環上分別對三個軸使用了PID控制器，使用MATLAB對其仿真實現，再調處良好穩定效果之后，在俯仰軸以及旋轉軸的外環上加入了動態矩陣控制以優化控制性能。并用MATLAB結合SIMULINK進行仿真實現，最終得到了相較于只使用PID控制器的系統而言，更為良好的控制效果。

參考文獻

Shan J， Liu HT， Nowotny S.Synchronised trajectory-tracking of multiple 3-DOFexperimentalhelicopters. IEEE Proceedings-Control Theory and Applications， 2005， 152（6）：683-692.

于明星， 王瑛， 邵帥. 基于Matlab的臨界比例度法在工程PID參數自整定數值模擬中的應用[J]. 遼寧師專學報（自然科學版）， 2018， v.20;No.78（02）：11-13+19.

劉鑫. 三自由度直升機實驗系統控制策略的研究[D]. 東北大學， 2008.

鉉佳歡. 動態矩陣預測控制的PLC實現及工業應用[D].

席裕庚， 耿曉軍， 陳虹. 預測控制性能研究的新進展[J]. 控制理論與應用， 2000， 17（4）：469-475.

席裕庚， 李德偉， 林姝. 模型預測控制——現狀與挑戰[J]. 自動化學報， 2013， 39（3）：222-236.

李小鶴. 廣義預測控制簡化算法的研究與分析[D]. 華北電力大學（保定）.