基于Simulink的兩級式單相離網光伏發電系統的仿真研究

國家太陽能光伏產品質量監督檢驗中心 ■ 夏元 惲旻 宋昊 吳兆 吳曉麗

0 引言

隨著能源和環境問題越來越嚴重，社會對于清潔能源的需求也越來越迫切，光伏發電得到了快速發展，各國對光伏技術的研究也日益重視。但光伏發電技術也存在一些不足之處，如造價成本高、電池轉換效率較低、用于光伏發電的硅片在制造過程中也會產生一定的污染等，而且光伏組件的輸出特性具有明顯的非線性[1]，受太陽輻照度和環境溫度的影響較大，因此，不能簡單的將光伏組件作為直流電壓源來研究。本文主要基于Simulink模塊下的Subsystem和S-function builder模塊，利用C語言編程簡化太陽電池數學模型編程，搭建了改進后的實用性較強的光伏組件仿真模型，不需要復雜的電池內部參數即可模擬不同輻照度和組件溫度下光伏組件的I-V和P-V特性曲線，然后根據Boost電路和電壓滯環跟蹤逆變技術進行了兩級式單相離網光伏發電系統的仿真，輸出結果具有良好的穩定性，為光伏發電系統的研究提供了方便。

1 光伏組件建模仿真

1.1 光伏組件的數學模型

光伏發電的主要原理是利用半導體界面的光生伏特效應將光能直接轉變成電能的一種技術。在純硅中摻入硼(B)原子形成p型半導體，在純硅中摻入磷(P)原子形成n型半導體，p型半導體和n型半導體在結合面形成深度為0.2 μm左右的p-n結；當光子照射到p-n結附近時，電子吸收光子的能量形成電子-空穴對，空穴由p極區向n極區移動，電子由n極區向p極區移動，從而形成電勢差，若在導體兩端連接導線就會產生源源不斷的電流。太陽電池的等效電路圖如圖1所示[2]。

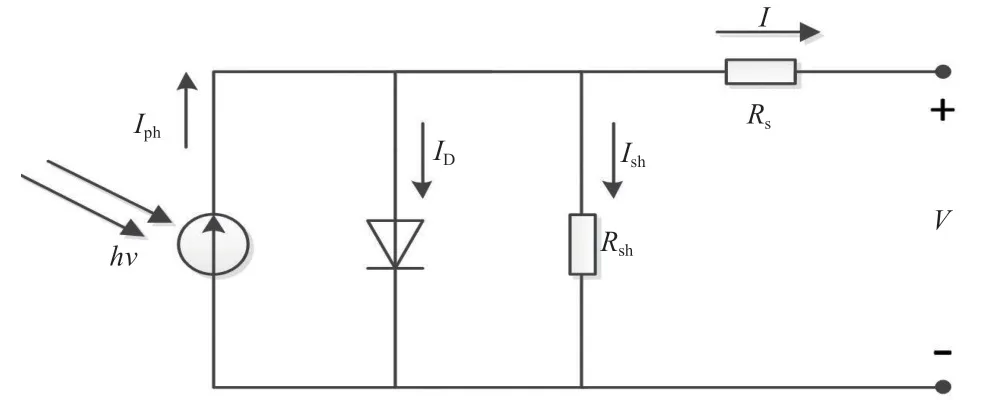
圖1 太陽電池的等效電路圖

圖中，hv為光子的能量；Iph為太陽電池的光生電流；ID為流過等效二極管的電流；Ish為流過并聯電阻Rsh的電流；I為太陽電池的輸出電流；V為太陽電池的輸出電壓。

由圖1可知，太陽電池的輸出電流方程為：

其中：

式中，I0為太陽電池在無光照時的反向飽和電流；q為電子電荷，取值為1.602×1019C；K為玻耳茲曼常數，取值為1.38065×10-23J/K；A為太陽電池的二極管曲線因數；T為太陽電池的溫度；Rs為太陽電池的串聯電阻。

將式(2)代入式(1)可得：

光伏組件由n個太陽電池串聯而成，其等效電路圖如圖2所示[3]。圖中，I1、V1分別為光伏組件的輸出電流和輸出電壓。

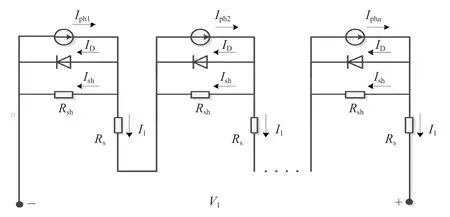
圖2 光伏組件的等效電路圖

根據圖2，光伏組件的輸出電壓方程為：

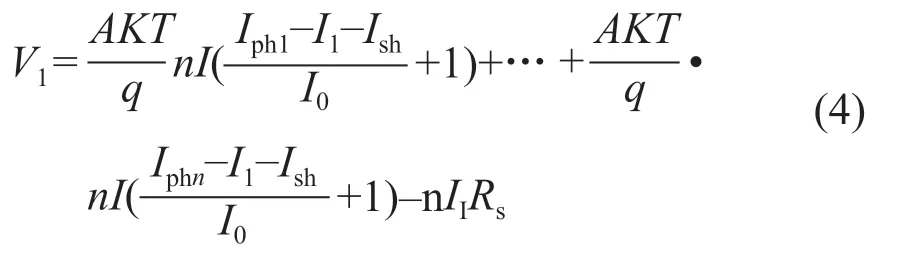
其中：

在進行理想電路計算時，令Iph=Iph1=…=Iphn，因此，式(4)可變換為：

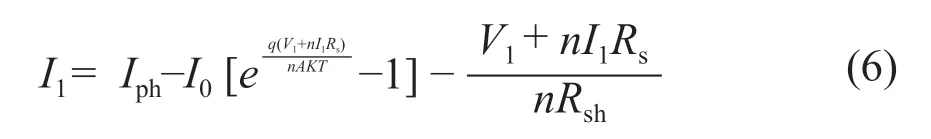
式(6)中，由于nRsh很大，使遠小于光生電流Iph，因此該項可忽略；且光伏組件短路時，其輸出電流I1(此時為Ish)遠大于光伏組件二極管正向導通電流ID，則有Iph=Isc。因此，可將式(6)等效為：

式中，Rs1為光伏組件的串聯電阻；I0為光伏組件在無光照時二極管反向飽和電流；Isc為STC條件下光伏組件的短路電流；A1為光伏組件二極管曲線因數。

光伏組件參數最直接的來源為組件背板上的在STC條件下的銘牌數據。根據文獻[4]，在STC條件下式(7)可轉換為：

其中：

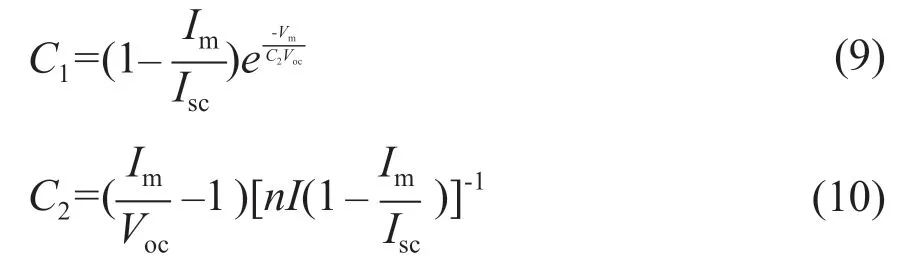
式中，Voc為STC條件下光伏組件的開路電壓；Vm和Im分別為STC條件下光伏組件最大功率點處的電壓和電流。

根據IEC 60891-2009《光伏器件——測定I-V特性的溫度和輻照度校正方法用程序》中的修正公式可知，輻照度和溫度變化所引起的電流和電壓的變化記為ΔI和ΔV，即：

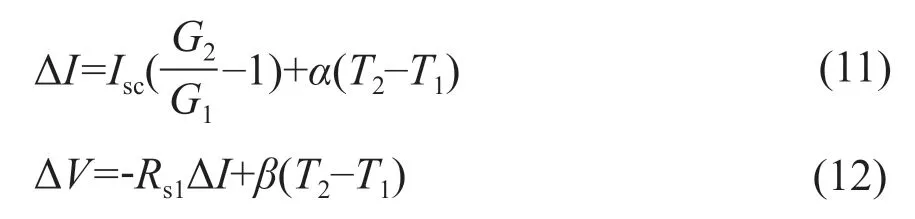
式中，G1為STC條件下的輻照度，取值1000 W/m2；T1為STC條件下的組件溫度，取值為25 ℃；G2和T2分別為任意條件下的輻照度和組件溫度；α和β分別為組件的短路電流溫度系數和開路電壓溫度系數。

任意輻照度和組件溫度條件下光伏組件的I-V輸出方程為：

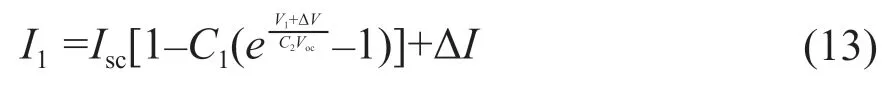
1.2 光伏組件的仿真模型

利用Simulink模塊下的Subsystem和S-function builder模塊，以C語言編程簡化太陽電池數學模型編程，搭建了具有電氣屬性的光伏組件仿真模型[5]，如圖3所示。其中，R為光伏組件外接可調負載，“out+”和“out-”分別為組件的正、負極輸出端，Subsystem模塊是光伏組件的模型主體。

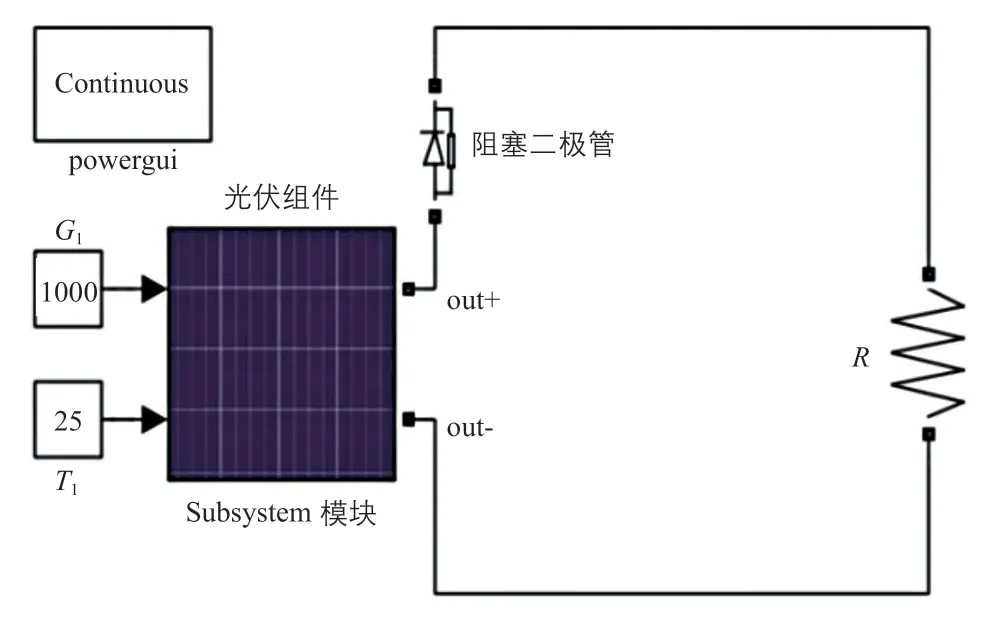
圖3 光伏組件仿真模型

光伏組件仿真模型主體Subsystem內部結構如圖4所示，將組件理解為可控的電流源，在S-function builder模塊內部界面用C語言編寫C-MEX文件的S-function，在Matlab主界面設置MEX-setup來配置編譯器，最終得到光伏組件的仿真模型。通過輸入不同的G2和T2值即可得到不同輻照度和溫度條件下組件的輸出曲線。

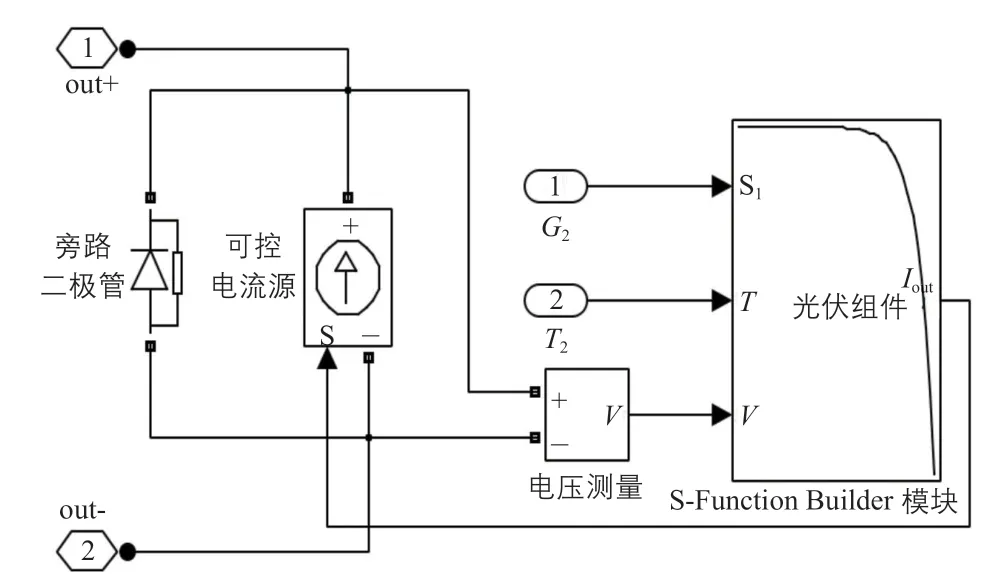
圖4 Subsystem模塊內部結構

1.3 光伏組件仿真模型的仿真結果

設置仿真環境參數為G1=1000 W/m2、T1=25 ℃，自動調節外接負載R的電阻值大小，對組件輸出電壓、輸出電流進行連續采樣，將采樣的數據繪制成I-V曲線，如圖5a所示。同時，在不同輻照度和溫度條件下，對光伏組件P-V特性曲線進行仿真繪制，如圖5b所示。在仿真過程中減小仿真步長，增加數據采樣點，可以提高曲線的平滑度。可以看出，圖5中的曲線均具有良好的穩定性，進一步驗證了模型的有效性。

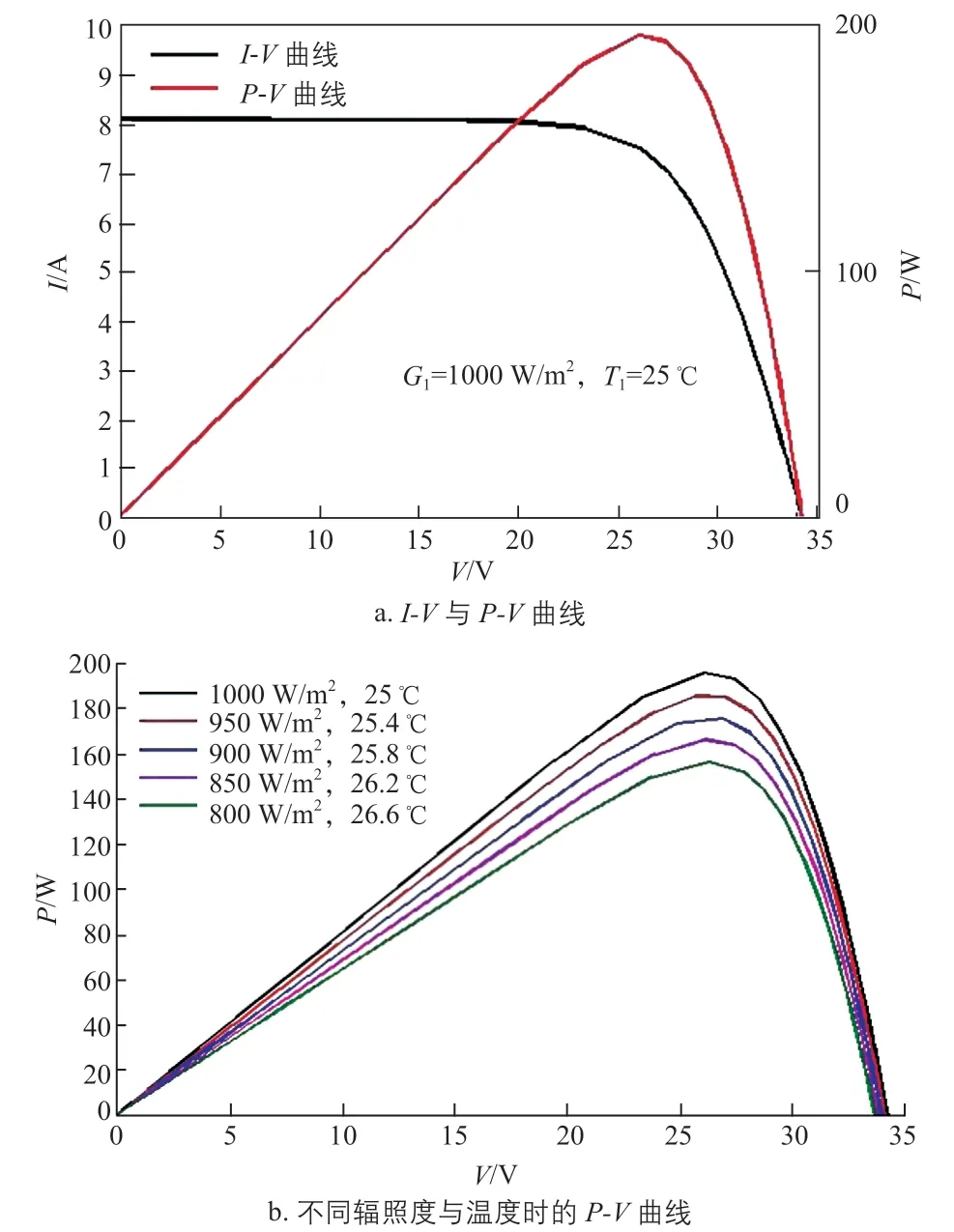
圖5 光伏組件的仿真曲線

2 兩級式單相離網光伏發電系統仿真

在Simulink下搭建了兩級式單相離網光伏發電系統的模型，光伏陣列由2個組串(每個組串由9塊光伏組件串聯而成)并聯組成36 kW的仿真系統。利用Boost電路對光伏發電系統輸出電壓進行提升，同時對光伏發電系統的輸出電壓和輸出電流進行采集，然后作為反饋信號傳送至MPPT Control模塊，通過對前后采樣的數據進行比較，從而輸出不同數值的占空比PWM波作為控制信號來控制MOS管的通斷，形成閉環控制[6]，在電壓滯環跟蹤閉環控制方式下得到所需要的輸出波形。整個兩級式單相離網光伏發電系統仿真模型如圖6所示。

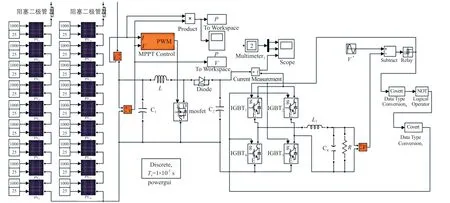
圖6 兩級式單相離網光伏發電系統的仿真模型

2.1 DC/DC升壓硬件單元

為保證逆變器直流側的母線電壓高于逆變器交流側的峰值電壓，通常采用Boost升壓電路進行配置，將光伏陣列輸出電壓升高到逆變器所需要的水平，同時可以根據DC/DC電路進行光伏陣列最大功率點跟蹤。其原理是通過改變MOS管開關器件的占空比來改變Boost模塊輸入側等效阻抗[7]，公式可表示為：

式中，Vi和Ii分別為Boost模塊的輸入電壓和輸入電流；D為MOS管器件門極輸入信號占空比；Rout為輸出側的等效阻抗。

2.2 MPPT控制建模

本文采用一種改進式擾動觀察法(P & O)，通過對光伏陣列的輸出電壓和輸出電流同時進行采樣，用乘法器計算光伏陣列的輸出功率，再與儲存的前一時刻的值進行比較，從而控制ΔU的正向或負向擾動[8]；將每次擾動步長進行累積，然后與鋸齒波信號進行比較，從而輸出PWM波來控制MOS管的通斷，原理如圖7所示。以鋸齒波表示載波信號的優勢在于當前累積的擾動步長值等于此刻的占空比，擾動步長越小，則跟蹤精度越高，從而使光伏陣列工作狀態更接近最大功率點。MPPT仿真模型如圖8所示。

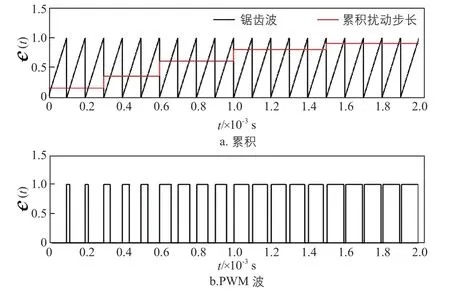
圖7 PWM波產生

將戶外實際光伏電站某一天中午時間段內采集到的輻照度和組件溫度數據進行整理，得到該時間段內輻照度和組件溫度的曲線，如圖9所示。

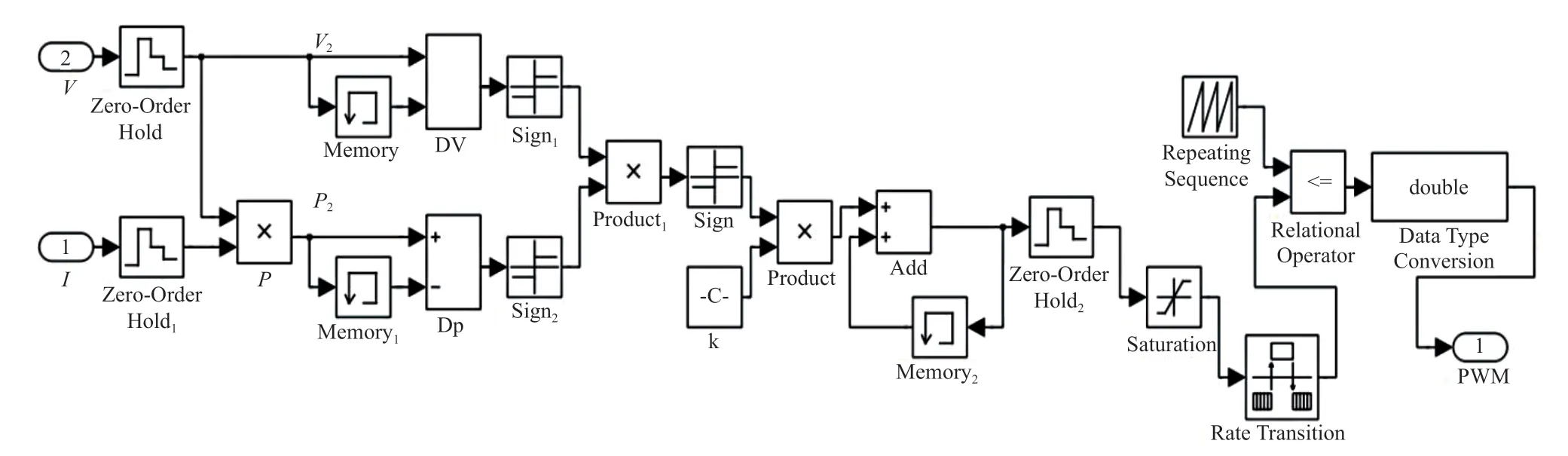
圖8 MPPT仿真模型

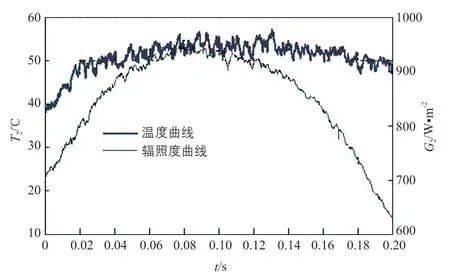
圖9 輻照度和組件溫度的曲線

分別在STC恒定條件及圖9所示輻照度、組件溫度變化的條件下，對光伏陣列模型的最大功率點進行仿真，通過Simulink的From Workspace模塊將圖9中實際采集的輻照度和組件溫度變化數據導入到光伏陣列仿真模型中，得到如圖10所示的波形。

在仿真模型中，由于未對光伏陣列母線電容C1設置初始電壓值，電容C1預先充電，從而使光伏陣列的實際輸出功率在仿真起始階段呈現先上升后下降的趨勢，系統在0.06 s基本趨于穩定。圖10a中的最大輸出功率跟蹤曲線具有良好的穩定性。由于圖9中的輻照度和溫度時刻無規律變化，導致圖10b中跟蹤的最大輸出功率隨之變化。圖9中，在0.14～0.20 s時間段內，輻照度呈現逐漸下降的趨勢，而溫度波動幅度小，導致該時間段內光伏陣列總的最大輸出功率逐漸降低。圖10b中最大輸出功率跟蹤曲線的后半部分驗證了這一點。

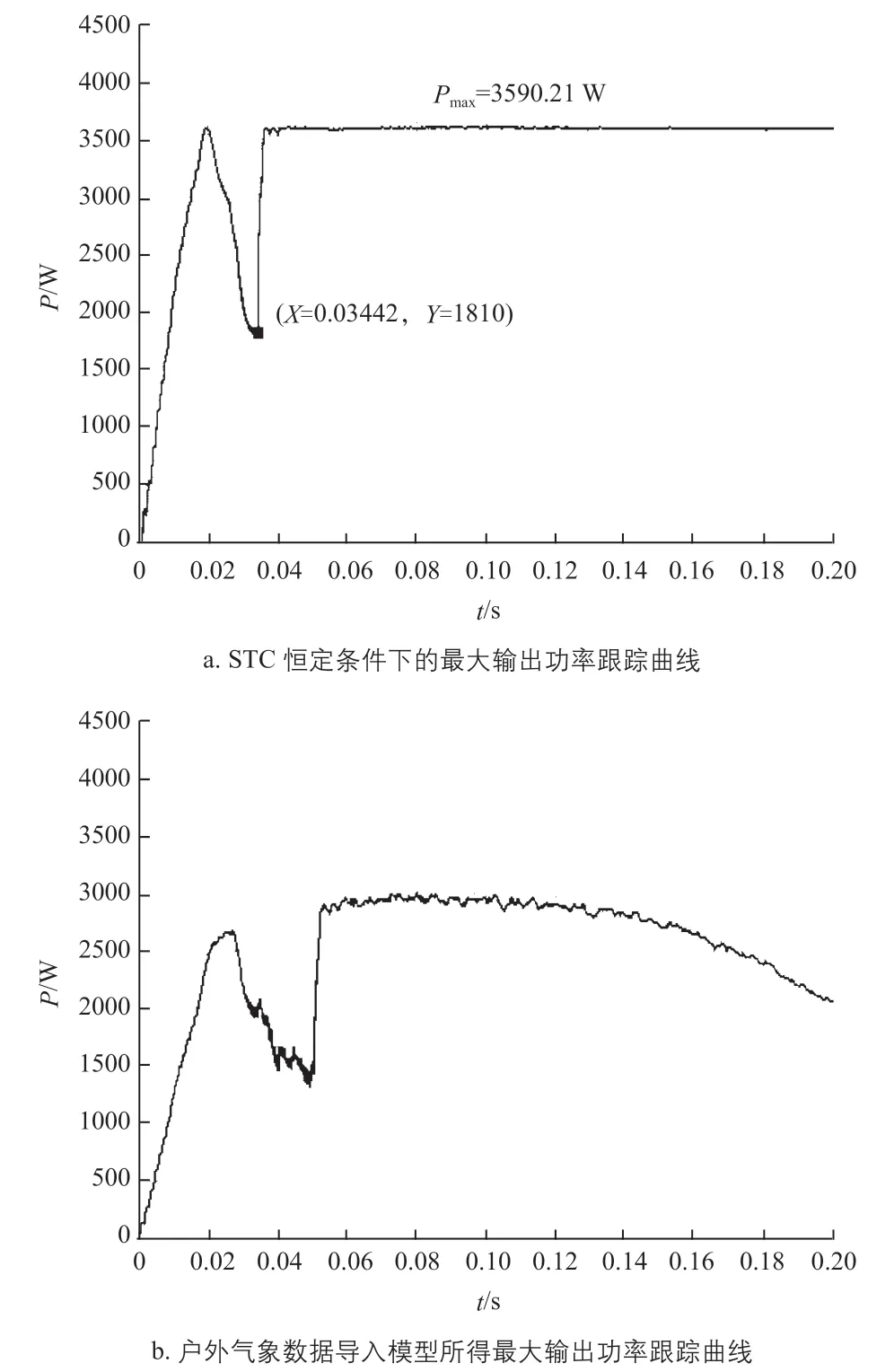
圖10 最大功率跟蹤曲線

3 DC/AC模塊仿真

傳統單相交流電壓的峰值和頻率分別為311 V和50 Hz，為獲得該類型的交流電壓，本文采取電壓滯環跟蹤式PWM逆變電路，通過負載電壓反饋信號與指令電流信號的比較產生PWM脈沖[9-10]，從而控制橋臂上的IGBT管通斷。其電路拓撲結構如圖11所示。

圖11 電壓滯環跟蹤工作原理

通過對環寬為2ΔU的滯環比較器進行控制，逆變輸出交流電壓就在Vref+ΔU與Vref-ΔU范圍內。當Vref電壓指令信號為正弦信號時，從輸出交流電壓V中濾去由功率器件通斷所產生的高次諧波后，所得的輸出交流電壓波形幾乎和Vref波形相同，從而實現對電壓閉環跟蹤控制。本文中將Vref幅值設置為311 V，頻率為50 Hz，濾波電容C3為30 μF，濾波電感L1為1.5 mH，其逆變輸出交流電壓和輸出交流電流波形如圖12所示。

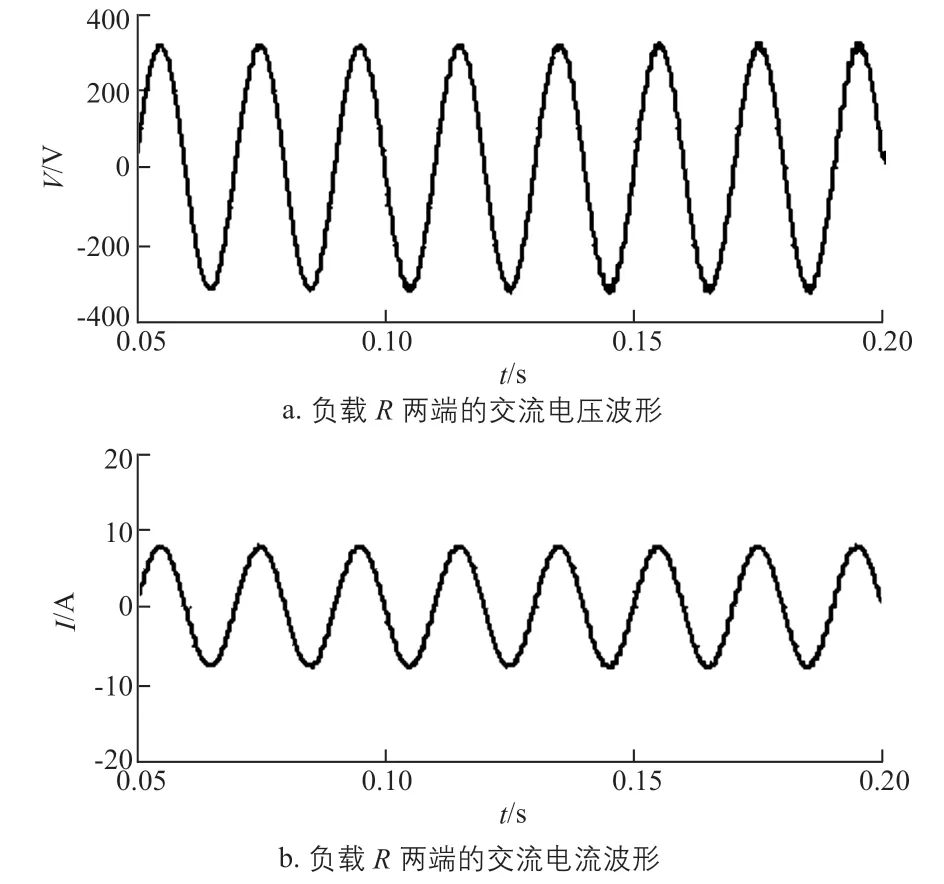
圖12 逆變輸出交流電壓和輸出交流電流波形

光伏陣列仿真離網輸出的交流電壓、交流電流波形保持了良好的正弦度，且相位一致。對輸出交流電壓進行離散傅里葉分析，得到各次諧波含量的對比結果如圖13所示。

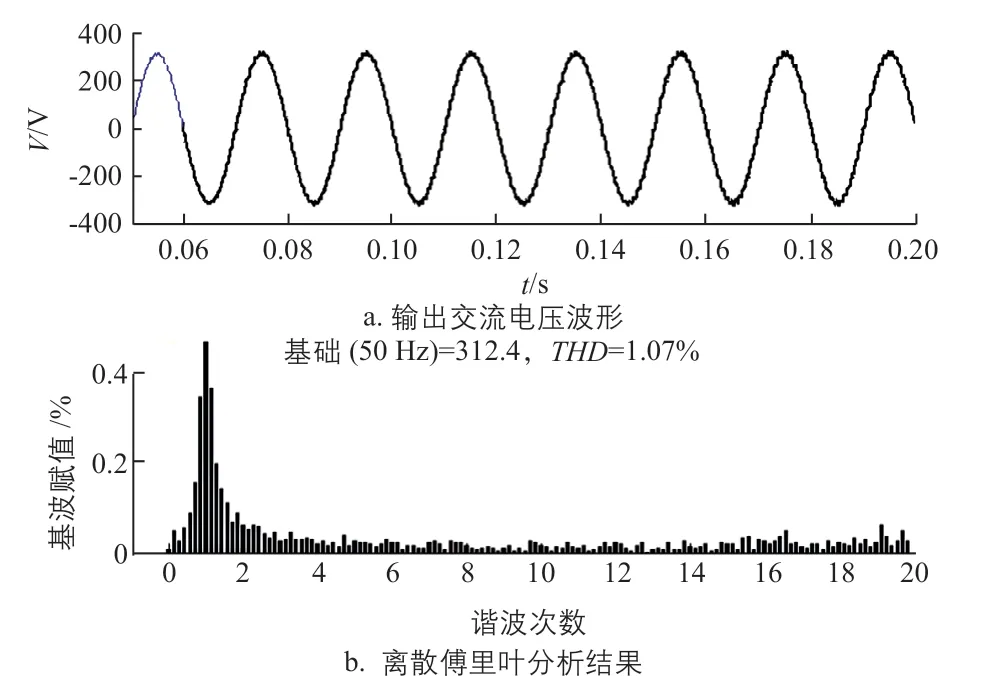
圖13 逆變輸出交流電壓的離散傅里葉分析結果

離網輸出交流電壓的THD=1.07%，滿足GB/T 19964-2012標準中的限值要求，輸出交流電壓諧波含量小，質量較好，可靠性高。

4 總結

本文基于S imulink搭建了光伏陣列的仿真模型，結合實際數據驗證了模型的準確性，針對光伏系統最大功率點跟蹤問題提出了一種改進式的擾動觀察法；然后結合Boost升壓電路搭建了MPPT仿真模型，當環境條件改變時，仿真系統能夠跟隨變化做出相應補償調整；最后基于電壓滯環跟蹤的控制方式對兩級式單相離網光伏發電系統進行了仿真，波形輸出質量較好，對實際的光伏發電系統設計具有一定的借鑒意義。