基于BP神經網絡的數字調制信號樣式識別*

袁 夢 程 莉 黨晶晶 時 愈

（武漢工程大學電氣信息學院 武漢 430200）

1 引言

在支持多頻段、多功能、多制式的軟件無線電臺中，如果不事先約定，通信收發雙方無法在某一特定的調制樣式上進行守候接收。因此，對信號進行解調前必須識別出接收信號的調制樣式及其他相關參數，才能解調出調制信號并對其做后續處理。

調制方式識別（Modulation Recognition）是指通過提取接收信號的特征，實現對非合作情況下信號調制方式的判斷，為后續解調選擇相應的解調方法提供依據［1］。

已有的信號調制樣式識別算法較多，特征參數的選取仍然是目前研究的重點［2］。有基于信號瞬時特征的調制樣式識別算法［3～6］、基于星座圖的數字調制方式識別算法［7～8］、基于譜相關函數的數字調制信號樣式識別算法［9］、基于高階累積量的數字調制信號樣式識別算法［10］等。

基于數字調制信號的瞬時相位、瞬時幅度和瞬時相位這三個瞬時特征值的數字調制信號樣式識別是目前最常用的方法之一。本文在文獻［11］中算法原理的基礎上對其特征值進行了修改，并針對幾種常見的數字調制信號提出了新的劃分方法，利用 BP神經網絡［12～13］對特征值進行驗證，通過實驗證明在高斯噪聲環境下信噪比大于等于10dB時正確率達到98%以上，表明該方法對于數字調制信號樣式的識別具有較好的效果。

2 特征參數提取

數字調制信號特征參數的提取主要圍繞三個關鍵：信號的瞬時幅度、瞬時相位以及瞬時頻率。但是基于這三個參數的特征值提取方法就不盡相同了，而且不同算法中相同特征值的劃分對象也不完全一致。

從文獻［11，14］中可知基于決策理論的信號調制樣式自動識別的基本原理和算法，主要包括五個特征參數的提取方法及劃分原理。本文在此基礎上對特征參數進行了修改，并提出了新的劃分方法，如圖1所示。其中γmax用來區分ASK與PSK或FSK；σaa用來區分2ASK與4ASK；σdf用來區分FSK與PSK；σaf用來區分2FSK與4FSK；σap用來區分2PSK與4PSK。

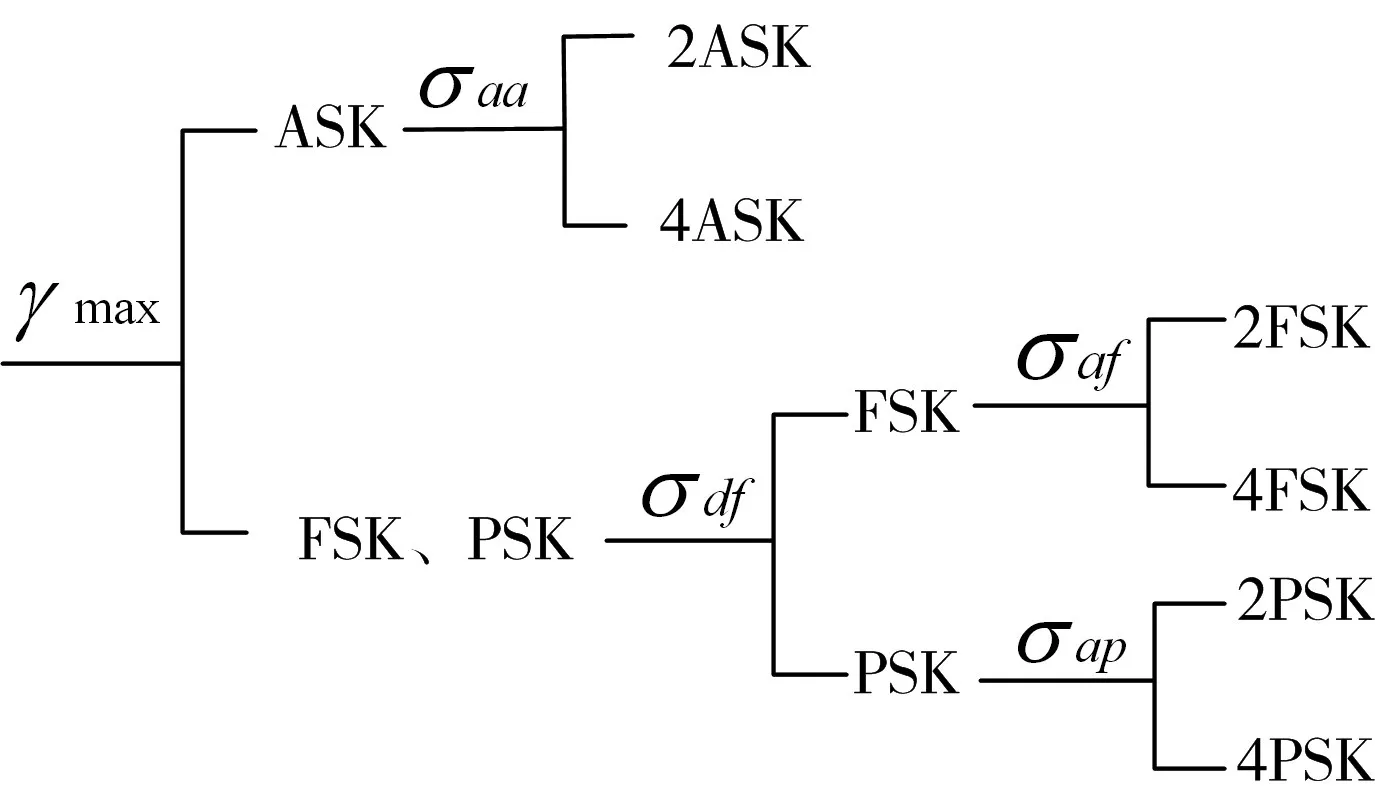
圖1 各特征參數及其劃分功能

2.1 歸一化零中心瞬時幅度之譜密度的最大值γmax

γmax定義如下：

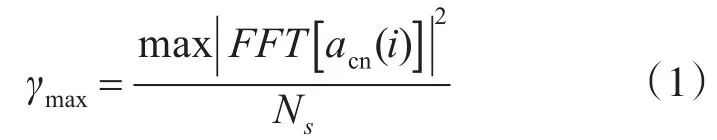
式中，Ns為抽樣點數，為零中心歸一化瞬時幅度，由下式計算：

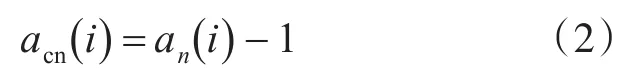
γmax主要利用幾種調制信號的幅度特性來區分恒包絡信號與非恒包絡信號，FSK與PSK的幅度值為常數，故其零中心歸一化瞬時幅度為0，而ASK信號由于瞬時幅度不為常數，故其零中心歸一化瞬時幅度不為零。

2.2 歸一化零中心瞬時幅度絕對值的標準差σaa

σaa定義如下：

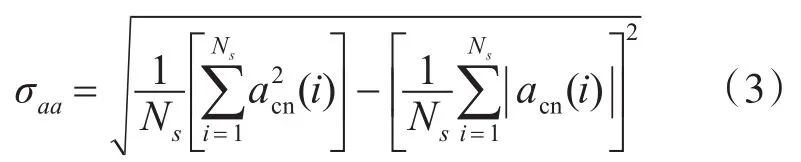
該參數主要用來區分2ASK信號與4ASK信號。2ASK信號有兩種幅度值，而4ASK信號則有4種幅度值。進行零中心歸一化后，2ASK信號瞬時幅度的絕對值應該約等于一個常數，則其標準差應該趨于0；而4ASK信號進行零中心歸一化后幅度的絕對值有兩個不同的值，因此其標準差不等于0。

2.3 非弱信號段零中心歸一化瞬時頻率絕對值的標準差σaf

σaf定義如下：

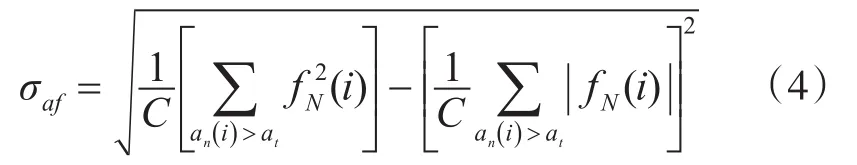
σaf用來區分是2FSK信號還是4FSK信號。因為對于2FSK信號，它的頻率只有兩個值，所以它的零中心歸一化瞬時頻率的絕對值是常數，則其標準差σaf為0，而對4FSK信號，由于它的瞬時頻率有4個值，零中心歸一化瞬時頻率的絕對值不為常數，因此σaf不為0。故可用σaf來區分2FSK信號與4FSK信號。

2.4 非弱信號段零中心歸一化瞬時頻率的標準差

σdf

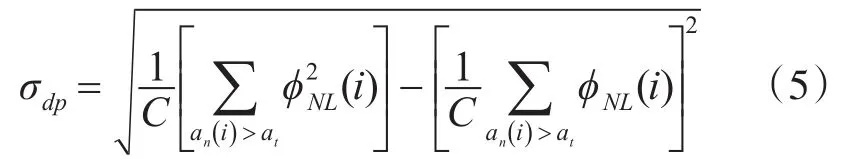
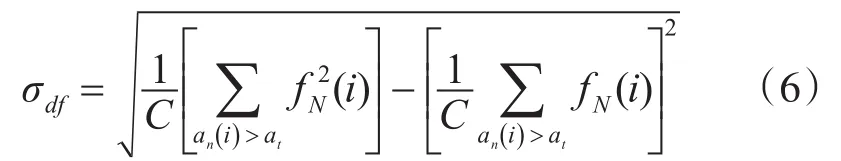
文獻［11］中σdp是用來區分ASK與PSK的，本文參考了σdp的計算原理，提出了新的特征參數σdf，定義如下：主要用來區分PSK信號與FSK信號。這兩種信號的最大區別就是頻率成分，PSK信號的瞬時頻率趨于常數，則其零中心歸一化瞬時頻率約等于0，而FSK至少有兩種瞬時頻率值，其零中心歸一化瞬時頻率值不為0，因此，利用零中心歸一化瞬時頻率的標準差即可劃分FSK與PSK。

2.5 相鄰采樣點瞬時相位差值的絕對值的標準差

σap

文獻［11］中提出的σap是利用零中心瞬時相位非線性分量絕對值的方差來區分PSK與ASK，但是該參數中瞬時相位非線性分量的提取會受到瞬時載波頻率估計值的影響產生較誤差，以致文獻［13］中依賴瞬時相位分線性分量的σap和σdp無法實現預期的劃分效果。因此本文改用相鄰采樣點的瞬時相位差值代替了瞬時相位非線性分量，提出了新的 σap。

σap定義如下：

該參數利用信號相鄰采樣點瞬時相位差值絕對值的標準差來區分2PSK與4PSK信號，在不考慮由采樣造成的相鄰采樣點之間的相位差值的情況下，2PSK信號相鄰采樣點的瞬時相位差值應該只有0和π；而4PSK信號鄰采樣點的瞬時相位差值應該有0、π/2、π及 3π/2（- π/2）四種。將其進行零中心歸一化，就可根據瞬時幅度和瞬時頻率同樣的原理來區分2PSK與4PSK。

根據文獻［11］中的原理，理想的瞬時相位非線性分量特性曲線中，2PSK信號的瞬時相位非線性分量包含2種幅度，而4PSK信號包含4種幅度，據此可以將這兩種信號區分開來。

但在實際情況中，利用希爾伯特變換得到的瞬時相位是線性分量的非線性分量的疊加和，要得非線性分量得先消除線性分量，也就需要得到準確的載波頻率。但是如果利用瞬時相位進行差分來模擬求導，得到的載波頻率誤差較大，也就無法得到較為精確的非線性相位分量，因此無法較好地實現特征參數的區分效果。

2PSK信號的兩種相位來自于載波的180°翻轉，而4PSK可以看成相位相差π/2的2PSK信號的疊加。因此我們可以通過載波的跳變來獲取這兩種信號的相位信息，即計算相鄰采樣點的相位差得到相位跳轉幅度，通過對所有的相位跳轉幅度進行統計，直接利用相位跳轉幅度這一參數來區分2PSK與4PSK。本文直接利用相位跳轉幅度的絕對值的標準差來區分2PSK與4PSK信號。2PSK與4PSK信號的相位跳轉信息如圖2所示。

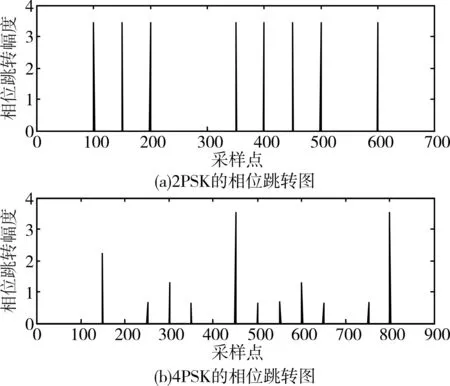
圖2 兩種PSK信號的相位跳轉圖

3 算法仿真及結果

3.1 BP神經網絡

BP（Back Propagation，反向傳播）神經網絡是一種按誤差反向傳播訓練的多層前饋網絡，其算法稱為反向傳播算法，BP算法的學習過程由正向和反向傳播兩部分組成，在正向傳播過程中，輸入向量從輸入層經過隱含層神經元的處理后（隱含層一般不超過2層），傳向輸出層，每一層神經元的狀態只影響下一層神經元狀態［15～16］。如果輸出層的輸出與預期目標的誤差大于預期誤差，則進行反向傳播，誤差信號從輸出層向輸入層傳播并沿途調整各層間的連接權值，以使誤差不斷減小，在達到設定的最大迭代次數或誤差大于預期誤差之前，將一直重復這樣的動作。

利用BP神經網絡算法進行分類識別主要包括預處理、訓練和學習、測試三個步驟。訓練和學習是在神經網絡內部自動進行的，主要取決于神經網絡結構及相關參數的設定。

3.2 特征參數生成

本文采用的BP神經網絡只包含一個中間層，輸入層節點數為5個，代表5個特征參數，輸出層節點為6個，代表6種數字調制信號，中間層結點設20個。神經網絡的學習率設為0.1，最大迭代次數為500，訓練的目標誤差為0.01。算法在Matlab中實現。

系統采樣率為100kHz，碼元速率為1000，載波頻率為5kHz，對已調信號進行10倍過采樣，得到的抽樣信號的采樣率 fs為50kHz。

圖3 六種數字調制信號的gama_max參數

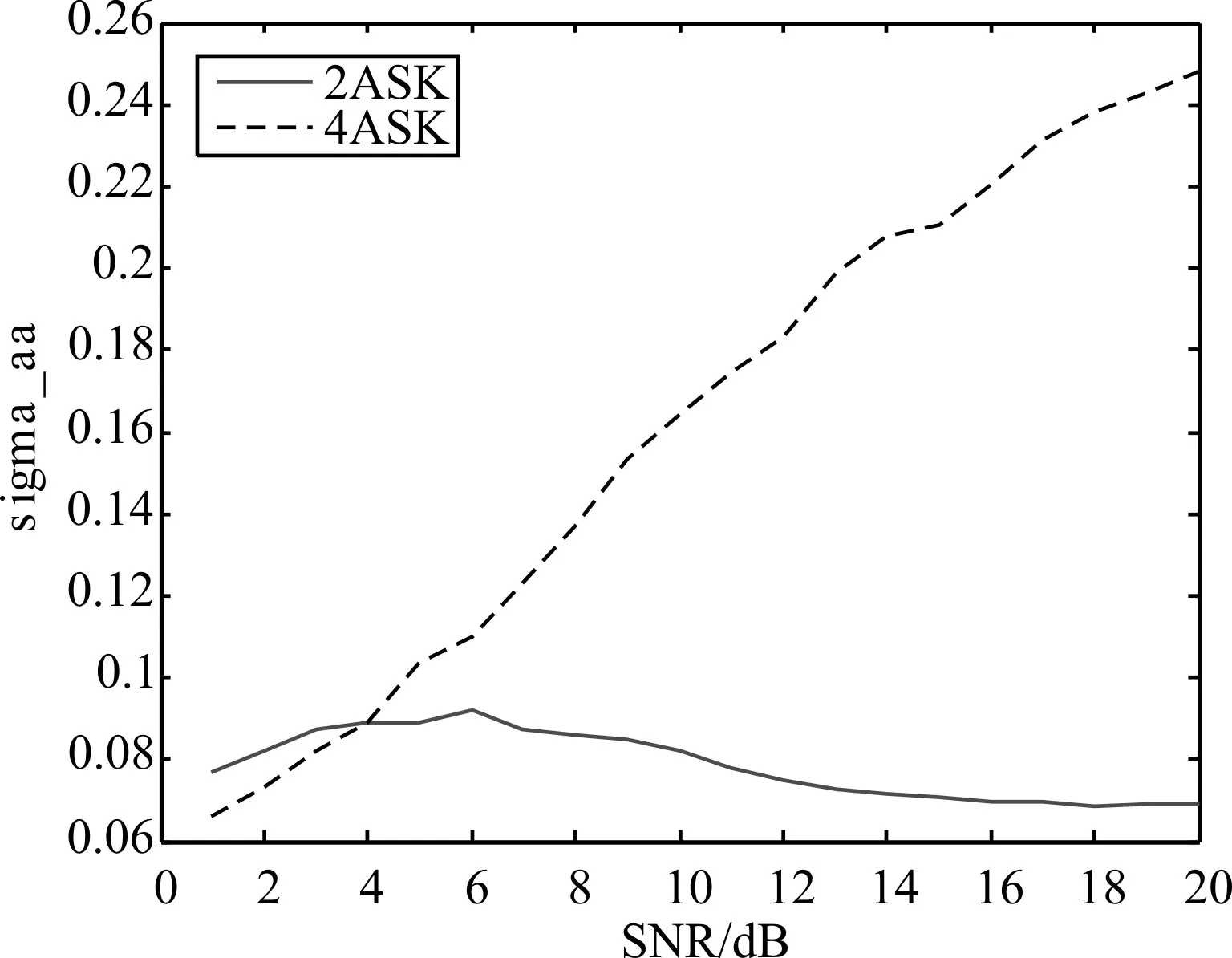
圖4 2ASK、4ASK信號的sigma_aa參數

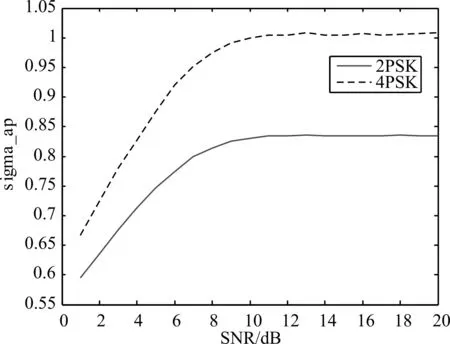
圖5 2PSK、4PSK信號的sigma_ap參數

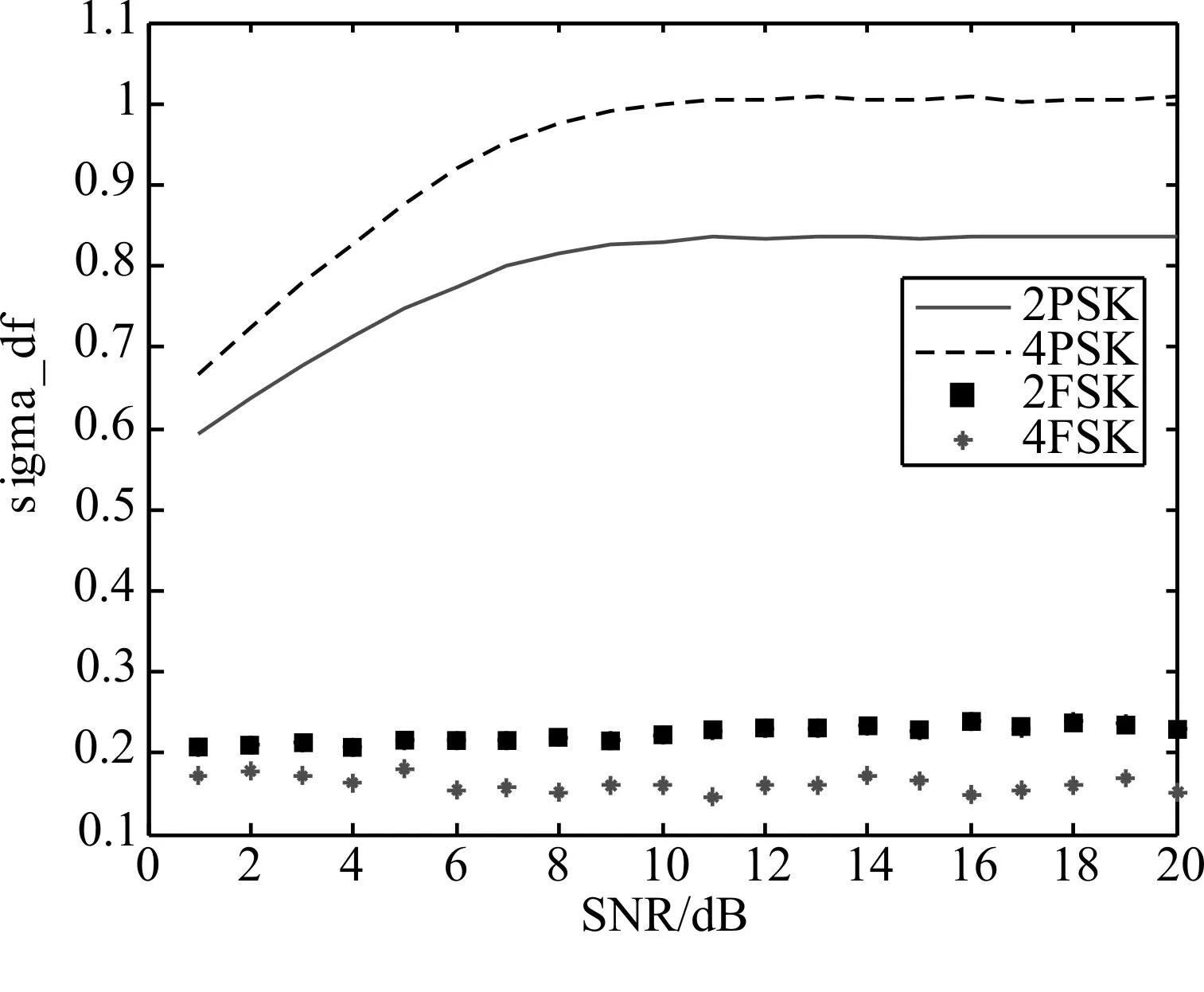
圖6 PSK、FSK信號的sigma_df參數

圖3 ～圖7為高斯白噪聲環境下，信噪比從1變化到20dB的情況下，不同數字調制信號的相同特征參數曲線的變化情況。觀察圖3可知，當信噪比低于4dB時，4ASK信號與FSK/PSK信號的gama_max值無法區分開來，信噪比從4dB開始上升至6dB時，ASK信號與FSK/PSK信號的gama_max值逐漸區分開來。從圖4可知，信噪比大于4dB時，根據sigma_aa參數可以區分兩種ASK信號。從圖5～圖7可知，sigma_ap、sigma_df、sigma_af這三種特征參數的劃分作用幾乎不受信噪比的影響，在低信噪比條件下也具有良好的劃分作用。

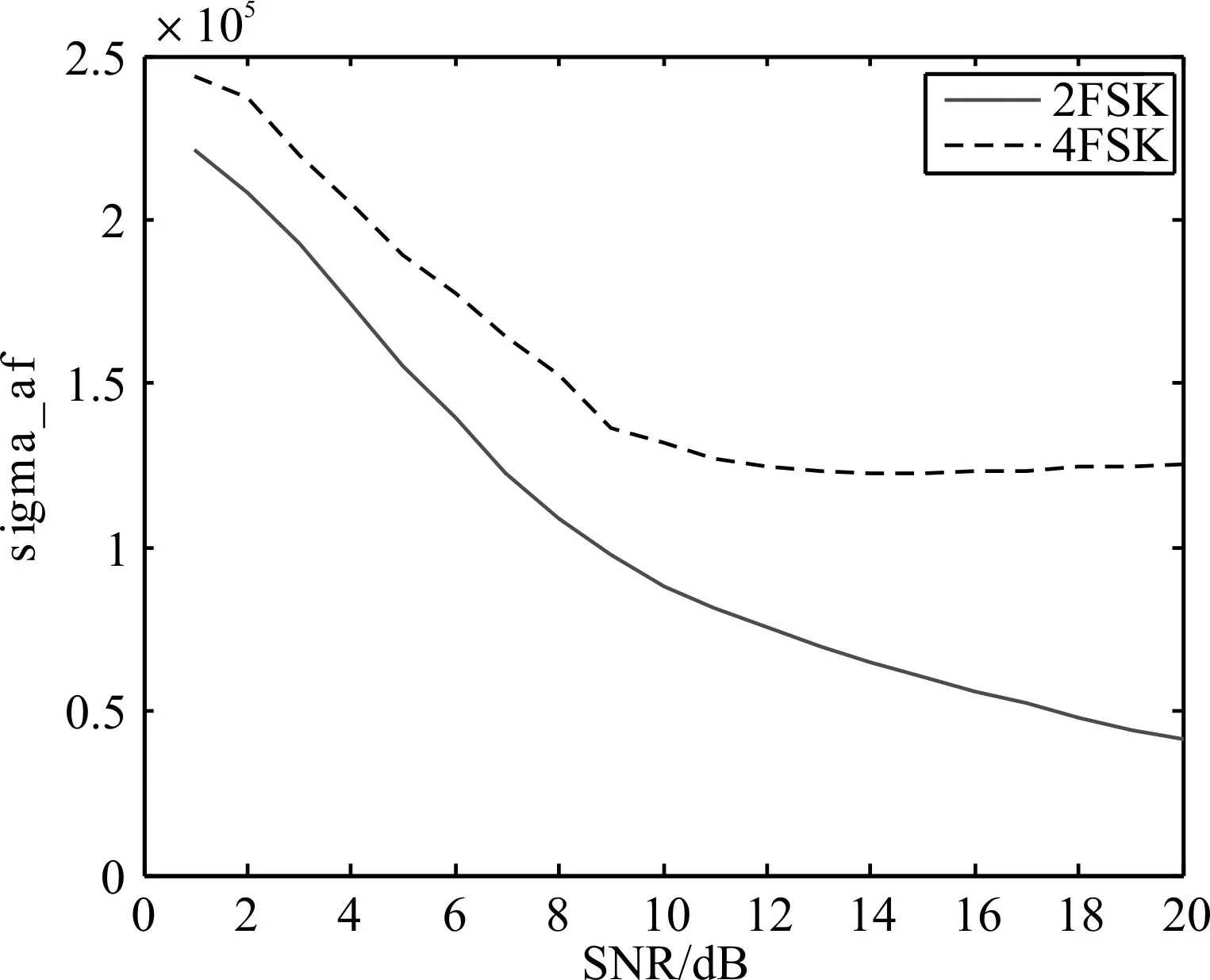
圖7 2FSK、4FSK信號的sigma_af參數

3.3 算法仿真

仿真共采用了200組含有加性高斯白噪聲的樣本信號，這200組樣本中，6種數字調制信號隨機分布，其中100組樣本用于BP神經網絡的學習和訓練，另外100組用于神經網絡的測試。

高斯噪聲背景下，幾種不同信噪比情況下的神經網絡仿真性能如圖8～圖11所示。

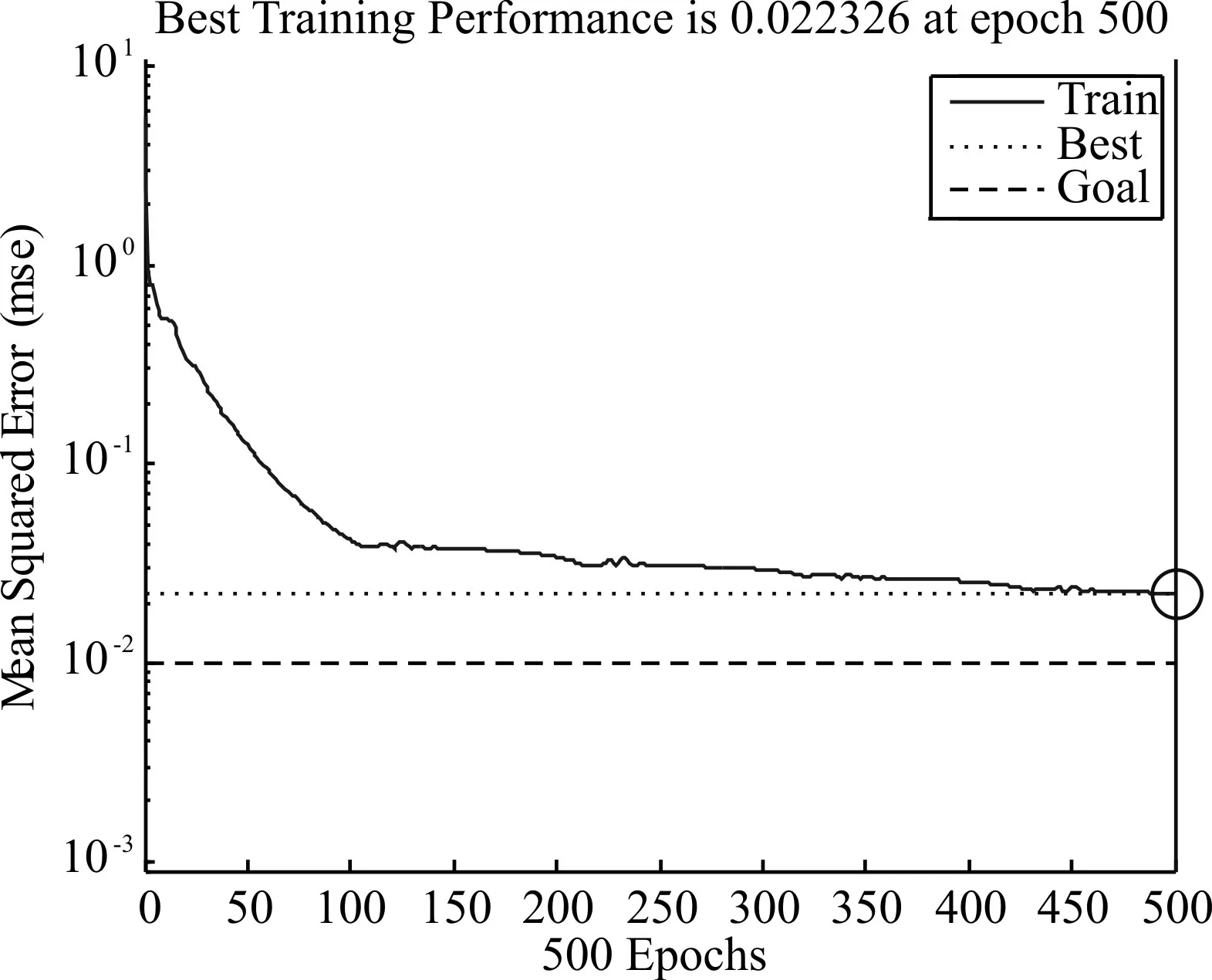
圖8 0dB條件下仿真結果

圖3 為高斯白噪聲環境下，信噪比為0dB時仿真結果：迭代500次后均方誤差為0.022，正確率為63%；圖4為高斯白噪聲下，信噪比為5dB時的仿真結果：迭代500次后均方誤差為0.064，正確率達到93%。其中正確率是通過統計神經網絡測試結果與期望信號類型是否相同而得到的。

圖5為高斯白噪聲環境下，信噪比為10dB時仿真結果：迭代193次后，均方誤差降低到0.0098，正確率達到98%；圖6為高斯白噪聲環境下，信噪比為15dB時的仿真結果：迭代95次后均方誤差降低到0.0097，正確率達到99%。

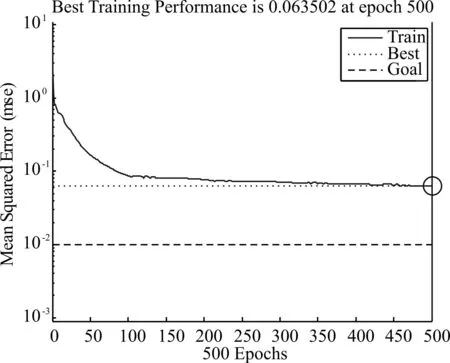
圖9 5dB條件下仿真結果

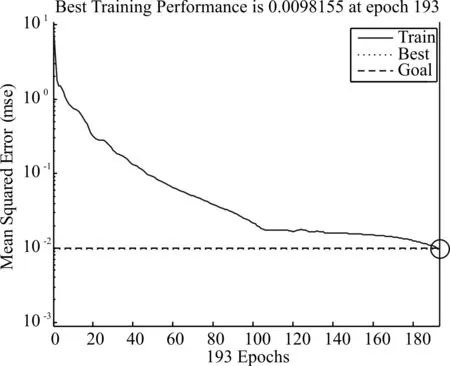
圖10 10dB條件下仿真結果

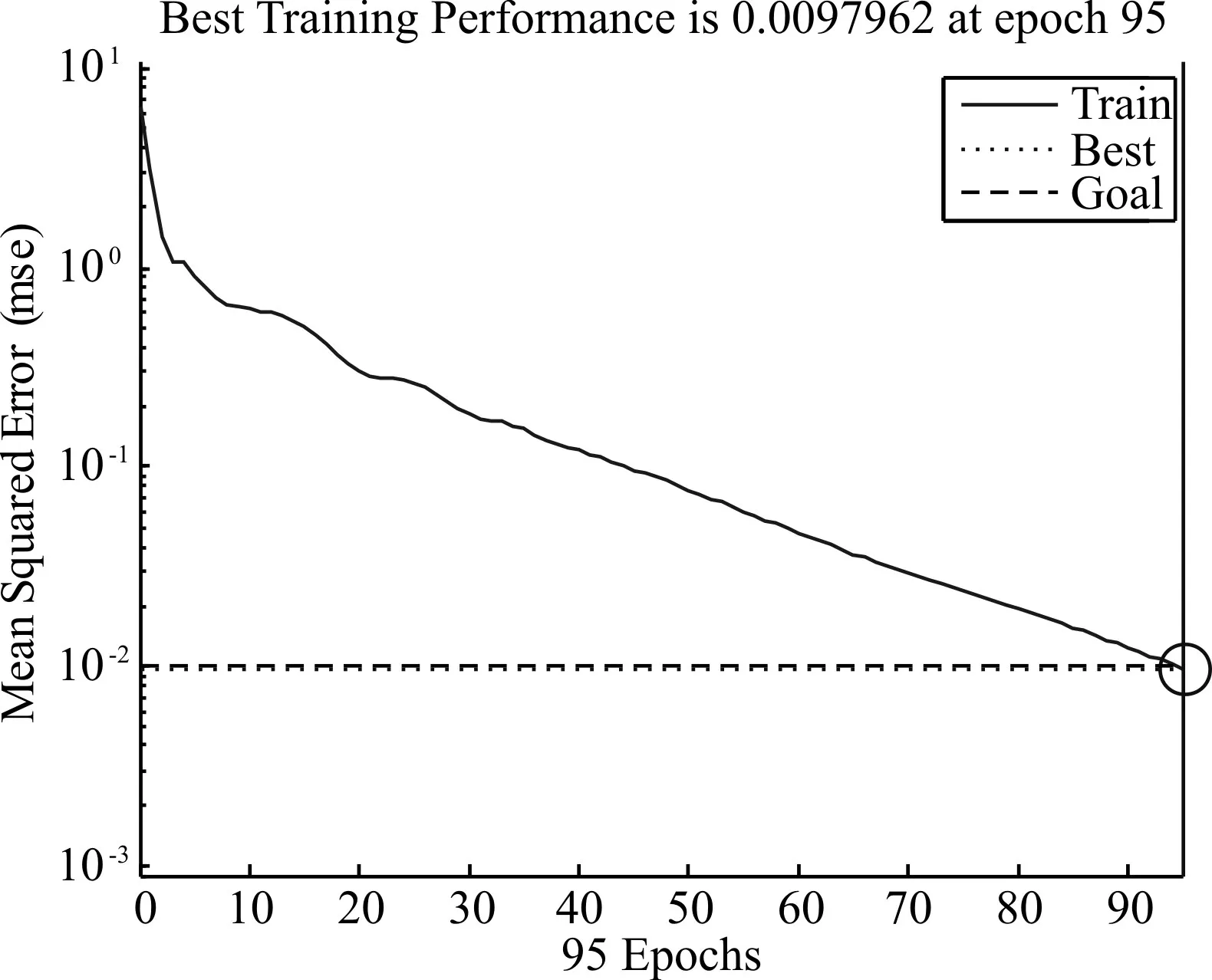
圖11 15dB條件下仿真結果

觀察這4幅圖可知，高斯白噪聲環境下，信噪比為0dB時，在神經網絡中完成預期設定的500次迭代后，均方誤差依然沒有達到預期目標，即10-2，正確率只有63%（通過統計得到）。信噪比為5dB時，在神經網絡中完成500次迭代后仍沒有達到預期最小誤差，均方誤差最低為0.022。當信噪比提高到10dB時，迭代193次后就提前完成了訓練目標，均方誤差達到了0.0098，正確率達到98%。

4 結語

本文在信號調制樣式自動識別的基本原理和算法的基礎上，提出了新的特征參數及其劃分范圍，用來實現幾種常見的數字調制信號的樣式識別，通過BP神經網絡對特征參數進行了仿真驗證。實驗結果表明，本文針對2ASK、4ASK、2FSK、4FSK、2PSK及4PSK這六種常見數字調制信號的識別提出的特征值提取方法，利用BP神經網絡進行訓練和測試，在SNR≥10dB時錯誤率可以降到10-2，具有較好的識別效果。