雙論域上基于加權粒度的多粒度粗糙集*

彭連貴 閻瑞霞 陳昭君

（上海工程技術大學管理學院 上海 201620）

1 引言

Pawlak粗糙集理論［1］作為一種處理不精確、不確定與不完全數據的理論，在人工智能、模式識別以及決策分析等方面得到了廣泛的應用和研究。

經典粗糙集理論的核心在于利用等價關系從近似空間中導出一對下、上近似算子。因此，粗糙集理論的研究主要集中在三個方面：等價關系、近似空間和論域。針對很多問題中論域上的二元關系不是等價的，學者們研究了基于相似關系、一般關系和優勢關系的粗糙集［2］；針對現實生活的模糊性和不確定性，學者們研究了模糊近似空間［3］、變精度［4］和灰色空間下的粗糙集［5］；粗糙集論域擴展的研究是從Yao［6］研究粗糙集代數的信任函數開始的，之后，學者們對論域擴展的粗糙集模型進行了研究。孫文鑫［7］將單論域擴展到了雙論域，擴展了其應用性；閻瑞霞等［8］考察了雙論域粗糙集的不確定性度量；張超等［9］將模糊語言與粗糙集融合，定義了一種新的粗糙集模型。

Zadeh L.A［10］在1996年提出并討論的模糊信息粒化問題之后，信息粒化理論［11］在集合理論和區間分析、模糊集、粗糙集、概率論、熵空間理論等架構內不斷的發展。Qian 等［12～15］通過分析粒計算與粗糙集理論之間的關聯，將粒計算和粗糙集結合起來并提出動態粒度理念，之后將單粒度粗糙集擴展到多粒度粗糙集。多粒度粗糙集模型作為一種新的多視角數據分析方法，克服了經典粗糙集理論的缺陷，在目標識別［16］、Web挖掘［17］、輿情預警決策［18］等眾多方面廣泛應用。

在多粒度粗糙集研究中，論域與粒度的權重問題一直是學者研究的熱點。孫文鑫將單論域擴展到雙論域上，卻忽略了在實際應用中不是每個粒度都是平等的，有的粒度比較重要，需要賦予更大的權重，而有的粒度作用小，可賦予較小的權重。張明［19］提出了基于加權粒度的多粒度粗糙集，差異地考慮了不同粒度在實際情況下具有不同重要度，卻沒有放到雙論域上進行研究。針對雙論域粗糙集在粒度重要程度上考慮的不足和加權多粒度粗糙集在論域擴展上的不足，分析并建立雙論域上基于加權的多粒度粗糙集模型，考慮雙論域內不同粒度重要程度的差異性，定義粗糙集模型的上下近似并對其性質進行了進一步的研究。

2 雙論域粗糙集

定義1［20］設U和V為兩個非空有限論域，設R是U和V上的任意二元關系集，且假設，為R的m個屬性子集族，′是V和U上R的逆關系。，R和R′的特征函數定義如下：

設論域U中有m個元素，論域V中有n個元素，利用特征函數定義R的關系矩陣記為

顯然R′的關系矩陣為矩陣A的轉置A'。如果關系矩陣A中不存在一行或一列元素全為零，則稱關系矩陣A為信息矩陣。

為了簡單描述，將論域U，V和關系R，R′構成的系統記為信息系統（U，V，R），其中U和V為兩個非空的有限論域，和互為逆關系。

定義2［20］在信息系統（U，V，R）中，，論域V到論域U的粗糙集近似算子P（U）為

3 雙論域上基于加權粒度的多粒度粗糙集

針對多粒度粗糙集論域擴展與屬性子集權重研究中的不足，分析并建立雙論域上基于加權的多粒度粗糙集模型，在將論域進行擴展的同時，考慮不同粒度所具有的權重的不同。下面給出雙論域上的基于加權的多粒度粗糙集模型的定義及其相關性質。

定義3設U，V是兩個不同的非空有限論域，設R是U和V上的二元關系集，包含n個屬性，且假設為R的m個屬性子集劃分，（U，V，R）為雙論域上的一般近似空間，，由R導出的粒度空間對應的粒度權重為，則對于?，X關于R的加權多粒度粗糙集的上下近似定義為

定理1設U，V是兩個不同的非空有限論域，設R是U和V上的二元關系集，包含n個屬性，且假設為 R 的 m個屬性子集劃分，（U，V，R）為雙論域上的一般近似空間，，由R導出的粒度空間對應的粒度權重為，則有

定理2設U，V是兩個不同的非空有限論域，設R是U和V上的二元關系集，包含n個屬性，且假設RT=｛R1，R2，…，Rm｝為 R 的 m 個屬性子集劃分，（U，V，R）為雙論域上的一般近似空間，0＜β≤1，由R 導出的粒度空間 U R1，U R2，…，U Rm對應的粒度 權 重 為，對 于，則有

定理3設U，V是兩個不同的非空有限論域，設R是U和V上的二元關系集，包含n個屬性，且假設為R的m個屬性子集劃分，（U，V，R）為雙論域上的一般近似空間，0＜β≤1，由R導出的粒度空間 U R1，U R2，…，U Rm對應的粒度權重為，有

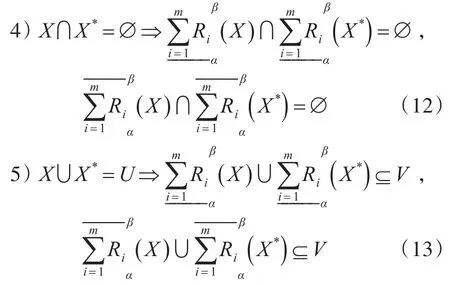
3）證明過程類似于2）。

定理4設U，V是兩個不同的非空有限論域，設R是U和V上的二元關系集，包含n個屬性，且假設RT=｛R1，R2，…，Rm｝為 R 的 m個屬性子集劃分，（U，V，R）為雙論域上的一般近似空間，0＜β≤1，由R導出的粒度空間 U R1，U R2，…，U Rm對應的粒度 權 重 為，則 對如果，則有

2）證明過程類似于性質（1）。

定義3設U，V是兩個不同的非空有限論域，設R是U和V上的二元關系集，包含n個屬性，且假設為的m個屬性子集劃分，為雙論域上的一般近似空間，0＜β≤1，由導出的粒度空間對應的粒度權重為，則對?Y∈U，X關于R′的加權多粒度粗糙集的上下近似定義為其中，稱為Y關于屬性子集族R′的雙論域上的基于加權粒度的多粒度粗糙集。

4 算例應用

雙論域上基于加權粒度的多粒度粗糙集在將論域擴展的同時考慮粒度的不同重要性的現實情況，在現實中的應聘案例中有很好的應用性。表1～3描述的是外貿公司選聘人才的情況，其中是由該外貿公司五位應聘者組成的一個論域，是由公司要求應聘者要具備的技能構成的一個論域。其中y1表示的是口才表達，y2表示的是專業技能，y3表示的是英語技能，y4表示的是工作態度。應聘者分別由一位主面試官，兩位副面試官為其打分，其中數字1表示該應聘者具備此項能力，0表示該應聘者不具備此項能力。

表1 專家1打分情況表

表2 專家2打分情況表

表3 專家3打分情況表

根據AHP方法，確定專家1、專家2、專家3對應的權重分配為。通過專家對應聘者的評估，我們知道這五位應聘者成功應聘的為。試問在滿足題設條件的情況下，這五位應聘者要想都應聘成功，必須具備哪幾項能力，應該具備哪些能力。根據定義3計算得

比較文獻［7］中粗糙集模型的運算結果發現：閾值β=2/3的題設情況下，雙論域粗糙集在進行運算時遍歷；而文中提出的粗糙集模型可以有選擇的訪問或來進行運算。且在計算機中設計運算時，首先選擇或，而不會選擇訪問，時間效率提高了33%；當在情況下，遍歷所有的屬性子集，必然造成冗余運算和時間的浪費；而雙論域上基于加權的多粒度粗糙集卻很好地克服了這一點，從可以知道，該模型在滿足一定權值積累的要求時即可；關注那些對事件發展具有顯著影響的因子，可以大大提高事件處理的效率。將該模型運算的結果。與文獻［19］模型的運算結果進行對比發現，該模型具有更高的精確度。

5 結語

粗糙集處理模糊信息的優越性，使其廣泛應用于諸多領域。為了克服雙論域上基于一般關系的多粒度粗糙集在屬性子集權重上考慮的不足與加權多粒度粗糙集在論域擴展問題上討論的不足，分析并建立雙論域上的基于加權的多粒度粗糙集模型。通過實例的分析驗證發現：該模型不僅在處理簡單問題具有很好的效果，而且在處理復雜事件時，也能夠很好地解決問題，同時在保證運算精度的情況下，節約運算的時間，提高效率。

文章提出一種新的粗糙集模型仍需要繼續深入研究該模型的不確定性度量和穩定性，以及在實際生活中的應用等問題，不斷將其優化，使其發揮更大的作用。