基于改進雙并聯過程神經網絡的光伏功率預測*

何祖軍 周光輝 楊奕飛

（江蘇科技大學電子信息學院 鎮江 212001）

1 引言

光伏發電具有高度的隨機性、波動性和間歇性，大容量并網會對電力供需平衡、電力系統的安全穩定以及電能質量產生不可忽視的影響。對光伏輸出功率準確預測，減少光伏輸出功率周期性和非平穩性對電力系統的不利影響［1］，合理制定常規能源發電和太陽能發電的需求策略，對推動光伏發電健康穩定發展具有重要意義。

當前以人工神經網絡為代表的預測模型應用較為廣泛，如BP神經網絡、灰色神經網絡、小波神經網絡、脊波神經網絡等預測模型［2］，從不同方面模擬了生物神經元的空間加權特性、自適應、傳導和輸出等大部分特性，但缺乏對于時間總和效應和延遲特性的描述［3］。本文采用的雙并聯過程神經網絡預測模型，對傳統的神經網絡結構進行了改進，改進后的模型對神經元的聚合運算機制和激勵方式向時間域進行擴展，放寬了對系統輸入的同步瞬時限制，使神經元同時具有時、空二維信息處理能力［4］。同時加入動量增項，對網絡權值進行修正，克服前饋神經網絡易陷入局部極小值的缺陷。仿真結果表明，該模型有效的提高了光伏發電功率的預測精度和穩定性，能夠滿足工程應用要求。

2 雙并聯過程神經網絡預測模型

2.1 雙并聯過程神經網絡預測模型

雙并聯前饋過程神經元網絡是在人工神經網絡的基礎上增加了輸入層至輸出層或某一最后隱層的直接全連接而形成的一種過程過程神經網絡模型［5］，其拓撲結構如圖1所示。

圖1 雙并聯前饋過程神經網絡拓撲結構

圖中是3層結構的雙并聯過程神經網絡拓撲結構模型［6］，設輸入層有n個節點，隱層有m個神經元，網絡的系統輸入向量為

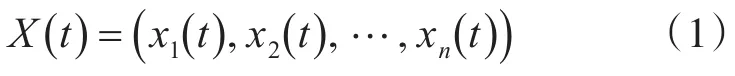
設系統輸入過程區間為［0，T］，則隱層第j個過程神經元的輸入為

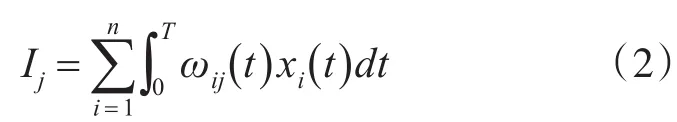
隱層第j個神經元的輸出為

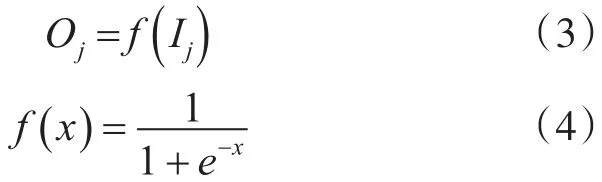
設輸出層的激勵函數g（z）為線性函數且g（z）=z。則網絡的系統輸出為

根據梯度下降算法，在一次學習迭代過程中網絡的待學習參數調整規則可規定為

式（7）～（9）中，r為學習迭代次數，α、β、γ為相應的學習速率。

至此，雙并聯前饋過程神經元網絡的基本學習算法可完整描述如下：

Step1：根據輸入輸出的時間序列，構建網絡的拓撲結構，隨機生成網絡的連接權值和閾值；

Step2：給定網絡學習誤差精度ε，學習迭代次數r=0，最大學習迭代次數M，學習參數和學習速率；

Step3：根據式（6）計算誤差函數E，如果 E＜ε或者r＞M ，則轉Step5；

Step4；根據式（7）～（9）調整網絡學習參數。轉Step3。

Step5：輸出預測結果，結束。

上述模型可以較好地解決大樣本的學習和泛化問題，可以滿足系統實時性的要求，解決了傳統前饋神經網絡缺乏在時間總和累積效應問題。但雙并聯過程神經網絡其核心部分仍然是前饋神經網絡，它繼承了神經網絡在尋優過程中極易陷入局部極小值的缺陷。本文提出的改進雙并聯過程神經網絡是通過改變過程網絡連接權值更新的方式優化網絡的尋優過程，克服網絡易陷入局部極值的缺陷。

2.2 改進雙并聯過程神經網絡預測模型

動態增量法在過程神經網絡訓練修正其權值時，不僅考慮傳播誤差在梯度下降上的作用，而且考慮在誤差曲面上變化趨勢的影響［8］，其作用如同一個低通濾波器，它允許忽略網絡上的微小變化特性［9］。利用動態增量法的作用則可能跳過這些局部極小值［10］。該方法是在過程神經反向傳播的基礎上在每一個權值的修正上加上一個正比于前次權值變化量的值，并根據前向傳播法來產生新的權值［11］。至此，式（7）的權值調整公式可改寫為

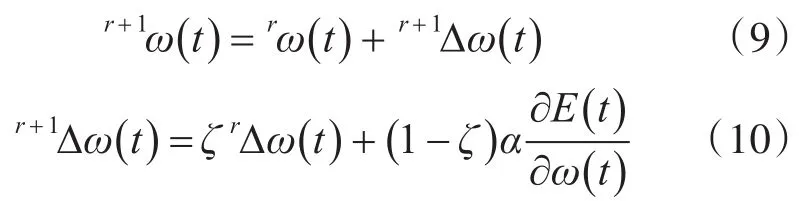
3 結果與分析

3.1 試驗說明

本仿真在Matlab2010b環境下，分別建立雙并聯過程神經網絡預測模型（PNN）和動態增量改進雙并聯過程神經網絡預測模型（DPNN）對同一實測光伏發電時間序列的發電量預測，并進行試驗對比。本文所使用的數據來源于澳大利亞艾利斯斯普林斯（Alice springs）的太陽能知識中心（Solar Centre Desert Knowledge Australia）裝 機 容 量 為5.5kW的第33號光伏發電實驗電站，包括從2017年6月10日到2017年8月10日每隔5分鐘輸出的光伏歷史數據（輸出功率）和同期的氣象數據（風速、溫度、相對濕度、太陽輻射照度）。經整理，共得到18146條訓練樣本數據，其中2017年8月10日的7：00～18：00的133條數據作為測試數據與預測數據進行比較。

3.2 結果分析

由于光伏輸出功率波動性較大，在訓練和預測時，需要對數據進行歸一化處理［14］，歸一化的公式為

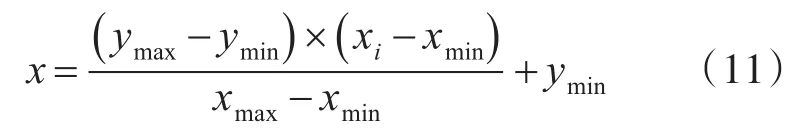
式中，xi為原始數據，為原始數據中的最大值和最小值；x為歸一化后的數據，ymin，ymax為歸一化處理的載波范圍。本文取ymin=-1，ymax=1。

光伏發電功率預測準確性暫時還沒有統一的評估標準，本文采用平均絕對誤差（MAPE）、均方根誤差（RMSE）等數據進行評估［15］，其公式為

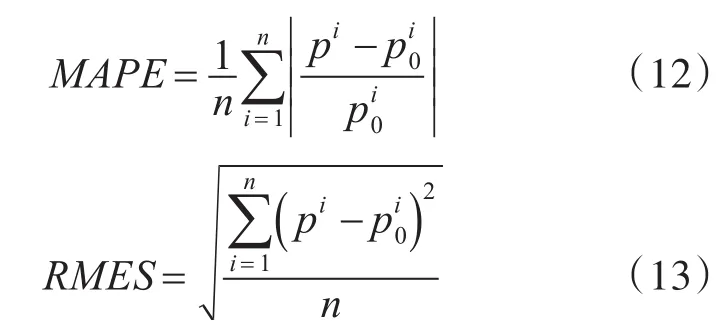
采用兩種不同方式建立的光伏發電功率預測模型。設定網絡的學習誤差精度為10-5；學習速率為0.001，最大迭代次數為1000次。其預測結果如圖2所示，相對誤差如圖3所示。

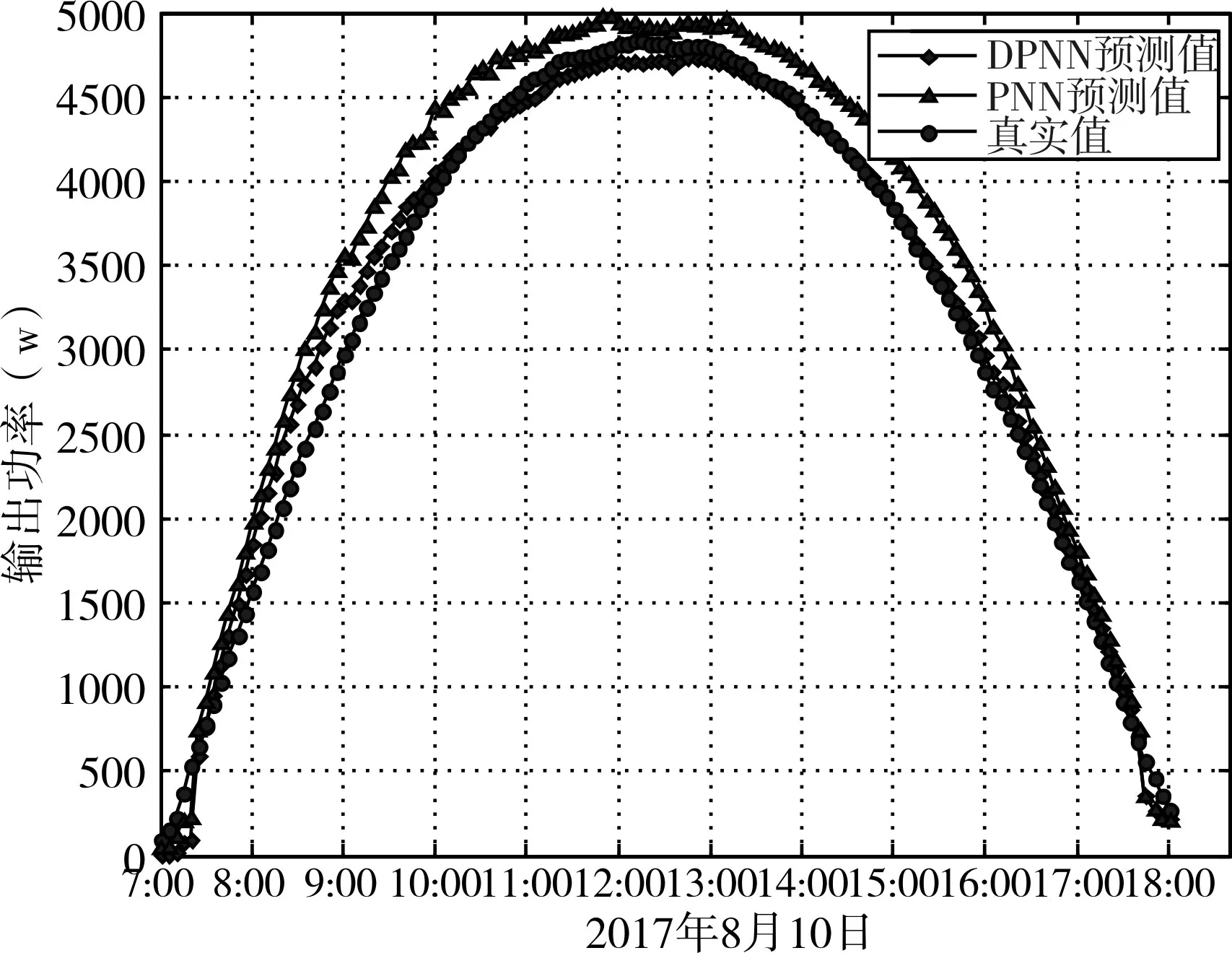
圖2 功率預測曲線

圖3 相對誤差曲線

由圖2和圖3可以看出，相比于雙并聯過程神經網絡的功率預測曲線，使用動量式改進后的雙并聯過程神經網絡預測曲線和實測輸出曲線更加吻合，相對誤差也更小。

為減小算法隨機性帶來的偏差，對每種模型運行10次［16］。表1是2種模型的MAPE值。表2是2種模型的RMSE值，分析表1、表2可知，雙并聯過程神經網絡建立光伏發電功率預測模型的平均絕對誤差的平均值為0.2530，偏差為38.88%；均方根誤差平均值為0.2584，偏差為31.90%。而經過改進后預測模型平均絕對誤差的平均值為0.1365，偏差為25.38%；均方根誤差最小值為0.1879，偏差為20.97%。可以看出，改進的模型尋優能力有了一定的提高，運行更加穩定，預測精度更好。

表1 2種模型的MAPE值

表2 2種模型的RMSE值

4 結語

本文針對雙并聯過程神經網絡算法建立的光伏發電功率預測模型易陷入局部極小值，運行不穩定等問題，采用動態增量式改進雙并聯過程神經網絡權值的修正方式，克服過程神經網絡算法易陷入局部極小值的缺陷。對比研究表明，動態增量式改進后的雙并聯過程神經網絡算法具有較強的全局尋優能力，可以有效地提高光伏輸出功率的預測精度和預測穩定性，具有一定的實用性和可行性。