基于自適應PSO的改進K-m eans算法及其在電子病歷聚類分析應用*

沐燕舟 丁衛平 高 峰 余利國 張 瓊

（南通大學計算機科學與技術學院 南通 226019）

1 引言

PSO是一種模擬自然界的生物活動以及群體智能的全局搜索算法，由Eberhart和Kennedy于1995年提出，該算法即具有進化算法的特點又與遺傳算法有相似的搜索及優化能力［1］。由于其自身的原理簡單、可調參數相對較少、編碼易于實現且應用效果明顯等特性，被廣泛地用于各類非線性問題的優化。但是PSO對于離散問題的優化則表現的不盡人意，往往會陷入局部最優解。如：黃太安等［2］提出了一種蛙跳簡化粒子群算法，將粒子群分多組同時收索，每組粒子進行多次迭代后在分組，從而保證了粒子間的差異性，避免了算法的早熟收斂問題。倪慶劍等［3］提出了動態可變拓撲策略來協調PSO的勘測能力，避免了算法陷入局部最優等。

聚類分析是將龐大的數據劃分為有意義的組，而在聚類分析的眾多方法中，K-means是最經典最常用的一種聚類算法［4］。K-means聚類是一種矢量量化的方法，最初來自信號處理，由于其處理數據相對簡單、快速，已經成為數據挖掘中的聚類分析的流行方法。然而，由于K-means算法本身對初始聚類中心較為敏感往往很容易陷入局部最優解［5］。針對這類問題，符保龍等［6］提出了一種基于均值密度中心估計的K-means聚類算法，Bandyopadhyay S等［7］介紹了一種利用K-means算法原理的基于遺傳算法的高效聚類技術，文獻結合了K-means和遺傳算法的優點，避免了陷入局部最優解。傅濤等［8］將PSO和K-means算法結合在一起用于網絡入侵檢測分析，其誤報率大大降低。

綜上所述，我們不難看出上述算法都在一定程度上緩和了原始PSO或K-means存在的一些問題，但是由于醫療病歷數據具有明顯的異構性、數字表征不明顯、數據本身的多樣性等特點［9］，這兩類算法并不能夠很好地處理分析復雜多樣的醫療數據。因此，本文提出了一種基于自適應PSO的K-means算法，該算法設計了一種自適應慣性權重函數對PSO進行動態調整，然后與K-means算法融合，使K-means的各個初始聚類中心能自適應生成，具有了更好的全局尋優能力。該算法融合了以上兩種算法的優點具有更高的電子病歷病癥聚類準確率和執行效率。

2 改進的自適應PSO

2.1 標準PSO

算法中每個粒子的速度向量定義為vi=（v1i，v2i，…，viD），位置向量定義為 xi=（x1i，xi2，…，xD），將每個粒子在迭代中的歷史最優pBest設為

i當前位置，群體中最優的個體作為當前的pBest。在每次迭代過程中，分別計算每個粒子的適應度函數值。若粒子當前適應度函數值優于歷史最優值，則將歷史最優pBest更新為當前位置。當該粒子的歷史最優比全局要好，則該粒子的歷史最優替代全局最優pBest。

粒子i的第d維的速度和位置更新公式［10］如下：

其中i代表粒子編號，d為求解問題維數，c1和c2代表非負常數學習因子，rand1d和rand2d表示區間［0，1］上的隨機數，ω為慣性權重，一般初始化為0.9。

2.2 自適應PSO

本文提出了自適應慣性權重ω，更新公式如下：

其中N表示粒子總數，n表示集合中粒子的個數，φ表示平衡系數，ρ表示粒子密度，表示最大慣性權重，表示最小慣性權重，t表示迭代次數。由式（4）可知，，則

，其中當迭代次數t（t＞0）增加時，由數學關系可以推導出逐漸增大而ω逐漸減小，結合式（1）就實現了PSO快速收斂，但又不會陷入局部最優的目的。在實際操作的時候，粒子群可以依靠這種關系來實現對ω值的調整，使得慣性權重始終在一個范圍內變化，更好地尋找全局最優解。即當粒子密度 ρ值大的時候，說明多數粒子靠近最優解，ρt2值隨之增大，由式（4）可知，ω值在逐漸減小，再結合式（1）就可以得到更精確的解。反之，當粒子密度ρ值變小，ω值在逐漸增大，從而進一步避免了早熟收斂情況的發生。這樣有效地調節v值的方式，讓式（4）達到了一種自適應的狀態，對于提高整個PSO算法的全局尋優能力有了很大的幫助。

3 基于自適應PSO的K-m eans算法

K-means算法的優點就在于它的簡單，所以在處理大量數據集的時候就意味著它要比其他的聚類算法執行的更快更有效。但是K-means算法也由于其對初始聚類中心點選擇的敏感性的問題，會造成聚類結果隨著輸入初始值的不同而波動，影響聚類的準確性。針對上述PSO算法和K-means算法的不足，本文設計了基于自適應PSO的K-means算法，其流程圖如圖1所示。

該算法具體子步驟描述如下：

輸入：待聚類數據集N，聚類數目k，粒子群的種群規模m，最大迭代次數IterMax；

輸出：聚類數據集的聚類中心不再變化的k個聚類劃分。

Step 1：初始化PSO；

1）從數據集N中隨機選擇k個中心點，將其作為粒子位置xi的初始值；

2）初始化粒子速度vi、個體最優位置 pBesti以及對應的個體極值f（pBesti）、群體最優位置gBesti及其對應的全局極值f（gBesti）；

3）Repeat m次；

Step 2：執行PSO；

1）按照適應度函數求得每個粒子的適應度值f（xi）；

2）對于每個粒子，如果粒子的適應度值f（xi）小于個體極值f（pBesti），則更新粒子的個體極值f（pBesti）以及個體最優位置pBesti；

3）如果所有粒子的個體極值f（pBesti）的最小值f（pBestimin）小于粒子群的全局極值f（gBesti），則更新粒子群的全局極值f（pBesti）以及群體最優位置gBesti；

4）根據式（4）動態調整慣性權重，并根據式（1）和式（2）分別進行更新每個粒子的速度和位置；

5）Until到達最大迭代次數IterMax；

Step 3：將Step2中得到的k個初始聚類中心作為K-means算法的初始值；

Step 4：將數據集中的點指派到距離最近的質點，更新每個簇的質心；

Step 5：重復Step4直到質心不在發生變化，算法結束。

通過對PSO慣性權重ω的自適應處理，有效地緩解了標準PSO算法中存在的早熟收斂及局部尋優能力較差的問題，提升了PSO算法全局尋優的能力，并將兩種算法的優勢進行互補以達到更好的聚類效果。

4 電子病歷聚類分析應用

隨著信息技術在各領域的廣泛應用，醫院也紛紛采取了電子病歷的方式管理醫療數據，與傳統的紙質病歷相比，電子病歷更以規范、方便、高效著稱［11］。隨著電子病歷數據持續的海量增長，基于電子病歷數據的聚類應用也應運而生。然而電子病歷數據聚類時很難達到預期效果，一方面，是由于其數據的海量性和主觀性，另一方面，更是異構性和數字表征不明顯的特性所致，所以傳統的聚類方法很難處理這類結構復雜的醫學數據［12～15］。

為了進一步驗證本文提出的基于自適應PSO的改進K-means算法在實際數據應用的效率，本文開展了電子病歷數據聚類分析實驗。實驗的環境：操作系統 W indows 7，處理器 Intel（R）Core（TM）i7-6567U CPU@3.30GHz，電腦內存 10GB，編程語言 Java，編程軟件 eclipse Mars.2Release（4.5.2），電子病歷系統相關頁面如圖2所示。

圖2 電子病歷系統頁面

該算法中的相關參數設置：學習因子 c1和c2取2.0，和取［0，1］區間的隨機數，ω∈［0.2，1.0］，聚類數目k初始化為16，粒子群的種群規模m為20，最大迭代次數IterMax設為100次。實驗數據是南通某醫院電子病歷中肝功能檢查數據，共有203254條的數據樣本，為了方便算法實施，經過數據預處理去掉了一些臟數據后得到以下6個屬性，具體數據格式如表1所示。

表1 電子病歷實驗數據表

實驗將標準K-means算法、PSO-based K-means算法和基于自適應PSO的K-means算法進行對比，實驗中采用將每種算法分別執行30次，并將測試的結果數據進行平均值運算（小數點后面取兩位）的方法來盡可能降低非算法和數據因素所導致的人為誤差。選取的部分數據集進行算法聚類準確率和執行時間對比結果如表2和表3所示。

表2 電子病歷肝病病癥的聚類準確率比較（%）

表3 電子病歷肝病病癥執行時間比較（ms）

由表2可以看出，針對4組不同規模的數據集，標準K-means算法和PSO-based K-means算法的聚類準確率都隨著電子病歷肝病數據量的增大逐漸下降，并且數據量越大下降幅度越大，原因就是K-means算法在初始聚類中心選取的敏感性問題上沒有得到很好地處理，由于聚類中心初值的過于隨機，影響了算法的執行準確率。而PSO-based K-means算法則是沒有考慮到電子病歷數據的特性，致使對肝病數據處理起來效率不高。本文算法在標準PSO算法的基礎上，通過對原始公式中參數慣性權重v的調整，使其有效地減小了粒子的早熟收斂，從而充分利用了PSO的全局尋優能力，并針對電子病歷數據的特點做了多模式數據源組合和數據變換的特殊處理，使其克服了電子病歷數據的復雜特性，因此能篩選出更合理的初始聚類中心。由表3和圖3可以看出，在數據量不大的時候，三種算法在處理數據的速度上差距不大，但是當數據量達到上萬條時，本文算法表現出了更優越的處理能力，直觀地反映在了處理數據消耗的時間上。

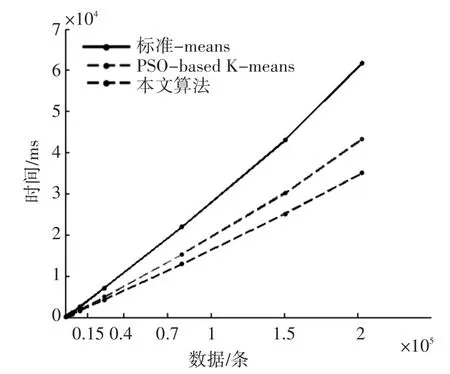
圖3 電子病歷肝病病癥聚類分析速率比較圖

5 結語

傳統的K-means聚類結果不穩定主要是算法初始聚類中心的隨機選擇所致，聚類結果隨著初始聚類中心的變化而變化，本文提出的基于自適應PSO的K-means算法，通過調整PSO的慣性權重v以求達到自適應，使得PSO充分的發揮了全局最優的特性，通過其優化生成K-means的初始聚類中心，從而避免了聚類結果陷入局部最優，最終訓練出可靠健壯的模型。本文算法應用于電子病歷數據的聚類分析，結果表明本文提出的基于自適應PSO的K-means算法在電子病歷數據聚類分析上的聚類準確率和效率明顯高于標準K-means算法和PSO-based K-means算法，這將有助于改善電子病歷數據的聚類質量，提高聚類算法在大數據醫療方面的挖掘效率。

傳統的數據挖掘算法如決策樹算法、神經網絡算法以及關聯分析算法在面對數據復雜多樣的電子病歷醫療數據時常常出現數據過擬合影響模型預測性能，訓練數據特征缺失影響模型訓練等一系列問題。在今后的研究工作中我們進一步將本文提出改進的基于自適應PSO的K-means算法應用到電子病歷其他病癥數據分析中，對不同病例開展分類和預測研究，進一步提高算法在處理醫療數據時的應用效率和范圍。