基于立德樹人的復習課教學
——以復習“全等三角形”為例

☉安徽省安慶市開發區實驗學校 秦 奮

一、學情分析

全等三角形是研究幾何中角、線段相等的重要工具，判定三角形全等的方法是研究角、線段相等的常用方法，三角形全等的應用是中考考查考生時必關注的一種能力.學生的知識零散地存儲在記憶中，這些知識點之間尚未建立一定的邏輯聯系，學生的邏輯推理能力尚未健全，尚不能在全局上、宏觀上駕馭和調控解題推理，時會時不會，得分增添了太多的偶然性.本節課從學生的心理特點、認知水平、思維方式和考前狀態出發，既立足于基礎，又螺旋拔高，兼顧了中等及中等以上學生的發展.

二、復習目標

（1）了解全等三角形的概念，掌握兩個三角形全等的條件.

（2）建立本章的知識網絡，應用相關知識解決實際問題.

（3）在圖形變換中，挖掘隱含條件，能熟練地找出全等三角形，關注學生邏輯思維能力、直觀想象能力、解題能力的培養，實現立德樹人的目標.

（4）鼓勵學生積極主動地參與到教學活動中，感受運用數學知識解決實際問題的樂趣，獲取成功的激勵，增強學生復習迎考的信心.

三、范例設計

1.知識梳理

圖1

例題：如圖2，請你選擇合適的條件填入空格內，使△DEF△DGF.

（1）因為DF=DF，___________，___________，根據SAS，可知道△DEF△DGF.

（2）因為___________，DF=DF，___________，根據ASA，可知道△DEF△DGF.

（3）因為___________，___________，DF=DF，根據AAS，可知道△DEF△DGF.

（4）因為DF=DF，___________，___________，根據SSS，可知道△DEF△DGF.

（5）若∠E=∠G=90°，___________，DF=DF，根據HL，可知道Rt△DEFRt△DGF.

設計說明：教師引導學生回顧三角形全等的相關知識.梳理本章知識結構，以例題為切入點，引導學生靈活選擇不同條件下三角形全等的判定條件，既厘清了學生對知識的系統性理解，又加強了學生學習能力的訓練.

圖2

圖3

2.例題呈現

如圖3，若△DEF AGB，你能得到哪些結論？

變式1：如圖4，若AC⊥BC，AD⊥BD，垂足分別為C、D，AC=BD，△ABC △BAD嗎？為什么？

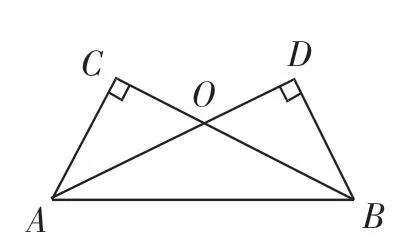
圖4

圖5

變式2：如圖5，AC⊥BC，ED⊥BD，BE⊥BC，垂足分別為C、D、B，AB=BE.試探究BE與AC+AD的關系.

變式3：如圖6，AC⊥BC，AD⊥BD，垂足分別為C、D，AD=BC.

圖6

圖7

（1）AE=BE嗎？請說明你的理由.

（2）如圖7，在上述條件不變的情況下，連接AB、OE，請判斷AB與OE的位置關系，并說明你的理由.

設計說明：通過呈現變式，展示問題的共性與變化.在題組解題思路的分析過程中，達到強化知識點的目的，滲透邏輯思維素養的培養.在教學中，教師應圍繞試題與解題兩個角度組織學生交流討論，激活思維.

圖8

圖9

3.中考題賞析

已知：點O到△ABC的兩邊AB、AC所在直線的距離相等，且OB=OC.

（1）如圖8，若點O在BC上，求證：AB=AC；

（2）如圖9，若點O在△ABC的內部，求證：AB=AC；

（3）若點O在△ABC的外部，AB=AC成立嗎？請畫圖表示.

設計說明：本題是安徽省中考題，考查的知識點主要是三角形全等的判定方法的運用和分類討論的數學思想.教師要引導學生分析題意，嚴密證明，寫出規范的證明過程，達到再次強化基礎、訓練技能的目的.尤其是第（3）題，該題對學生的作圖能力有較高的要求，教師在復習時應該予以強調，對相關知識之間的聯系與規律也要高度重視，增強知識遷移能力，使不同的學生有不同的收獲，達到數學學科立德樹人的目的，讓學生感受成功的喜悅.

4.精選練習

練習1：如圖10，給出下列四組條件.

圖10

①AB=DE BC=EF AC=DF

②AB=DE ∠B=∠E BC=EF

③∠B=∠E BC=EF ∠C=∠F

④AB=DE AC=DF ∠B=∠E

練習2：如圖11，△ABC中，D是AB的中點.將△ABC沿DE所在直線翻折，使點A恰好落在BC上的點F處.若∠B=50°，則∠BDF=______，∠ADE=___________.

圖11

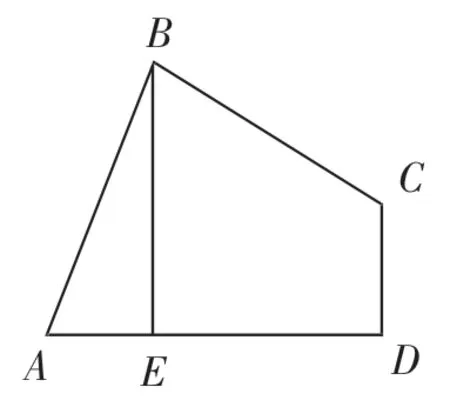
圖12

練習3：如圖12，四邊形ABCD中，AB=BC，∠ABC=∠CDA=90°.BE⊥AD于點E，且四邊形ABCD的面積為8，則BE=___________.

設計說明：根據本節課的復習內容，設置針對性強的練習，讓學生在實戰訓練中得以鞏固和提高，并通過有梯度的練習逐步拉伸學生的思維深度，提升解題能力.

四、教學思考

1.重視基礎知識和基本技能

在復習課的教學中，許多教師都片面地認為要拔高，要增加難度，其實基本知識點和知識框架仍然要給學生厘清，基礎不牢，地動山搖.而且在歷年的中考中，“三角形全等”經常會出一些中等難度的題目，所以教師在復習時不能走入誤區.

2.重視學生終身學習能力的培養

在復習課的備課中，教師首先要明確本節課要落實什么目標，如何組織教學以實現目標的落地有聲，選取什么樣的例題傳遞出目標信息.復習課的教學不是教什么知識或回憶什么知識，而是要培養學生的綜合素養，教給學生那些能讓學生具有終身學習能力的素養.學生的知識梳理、知識遷移、問題洞察、自變問題、自拓問題等，都是落實教學目標的體現，這是復習課教學的最終目的.教師在復習課中引導學生達成目標，是復習課教學的宗旨所在，即培養學生終身學習和終身發展的能力，也就是常說的學科核心素養.

總之，復習課教學尚是一個值得研究的課題，讓一節復習課收到事半功倍的效果，我們正在路上！