小題需大做，“滾”動出精彩*
——一節綜合與實踐活動課的教學實錄與思考

☉江蘇省南京市雨花臺中學 梁海波

一次九年級測驗后，學生對一道選擇題的答案爭議較大并展開了熱烈的討論.筆者結合學生的討論和思考，設計并上了一節綜合與實踐活動課“滾動的圓”，在公開課展示活動中受到廣泛好評.本文把課堂教學實錄整理如下，并將筆者的教學思考整理成文，以期與各位同行研討交流.

一、教學實錄

1.開門見山，抓住知識生長點

問題1：（原題改）將兩枚同樣大小的硬幣放在桌上，固定其中一枚，另一枚則沿著其邊緣滾動1圈，此時滾動的硬幣滾動了幾圈？

生1：1圈，兩枚同樣大小的硬幣說明這兩枚硬幣的周長是相等的，所以一枚硬幣沿著另一枚滾動1周，剛好就滾動了1個周長，也就是1圈.

師：有不同的答案嗎？

（大部分學生沉默，幾名學生站起來說“不對”，但講不清問題在哪兒）

師：既然通過思考無法確定結果，我們可以動手操作體驗一下.

學生活動：小組合作實驗，用瓶蓋模仿硬幣的滾動，動手操作驗證猜想，提醒學生注意滾動的過程中不要出現滑動.

（學生操作，教師提醒學生操作要規范）

師：大家都完成了實驗，實驗的結果是什么呢？

（多數學生說2圈，少數學生說1圈）

師：下面請一名同學來操作演示.

（生2實物投影展示，結果是2圈）

師：有沒有同學知道為什么呢？

（學生沉默）

師：本節課我們帶著這個問題來探究滾動的圓，剛才的操作中大家已經初步體會了圖形的滾動，但在圓上滾動的情形比較復雜，我們如何去研究一個復雜問題呢？

生：從簡單入手.

師：圓在什么圖形上運動比較簡單？

生：在直線上.

師：下面我們就從圓在直線上的滾動開始研究.

設計意圖：利用生活中的數學問題，創設有效的問題情境，讓學生的思維受到適度挑戰，激發學生的學習興趣.同時，通過回顧學生已有的知識和經驗，回歸解決問題的本質，將復雜的問題簡單化，從簡單、特殊的問題開始探究.

2.化“疑”為簡，尋找問題突破口

問題2：如圖1，將一個半徑為r的圓在直線上滾動1圈，則這個圓滾過的路徑長為？思考圖2中哪條線段長是圓滾過的路徑長.（動畫展示滾動過程）

圖1

生3：路徑長為2πr，線段AA1的長就是圓滾過的路徑長.

追問1：在圓滾動的過程中，什么沒有變？什么發生了改變？

生4：圓的大小和形狀都沒有改變，圓的位置發生了改變.

生5：圓與直線的位置關系也沒有改變，始終是相切.

追問2：圓心所經過的路徑是什么圖形？

（動畫展示滾動過程，如圖2）

圖2

生6：一條線段，圓心到直線的距離沒有改變，始終等于半徑.

追問3：這條線段多長？你有何發現？

生6：是2πr，我發現圓心經過的路徑長等于圓滾過的路徑長.因為圓O始終與直線l相切，所以OA和O1A1都與直線l垂直，那么OA平行且等于O1A1，則四邊形OAA1O1是矩形，即OO1等于AA1.所以圓心經過的路徑長等于圓滾過的路徑長.

問題3：若線段AB=4πr，則此半徑為r的圓從點A無滑動地滾動到點B需轉幾圈？

生7：2圈，用4πr除以2πr得2.

師：當圓在直線上滾動時，圓滾動的圈數應該怎么求？

生8：圓滾動的圈數等于圓滾過的路徑長除以圓周長，即等于圓心經過的路徑長除以圓周長.

設計意圖：回歸學生思維的最近發展區，探究圓在直線上滾動的過程，在變化中尋求不變.在操作中搭建學生思維的橋梁，尋求主線問題的突破口，體會直線上圓的滾動過程即平移與旋轉的復合運動.

3.拾級而上，操作中探究方法

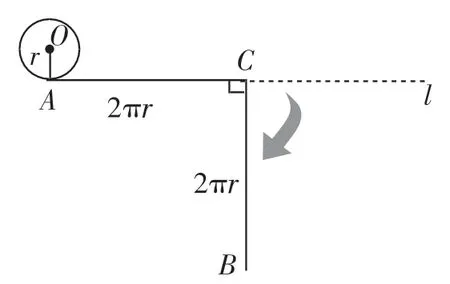
圖3

問題4：如圖3，將總長為4πr的線段AB在中點C處折成90°，此時這個半徑為r的圓從點A到點B需滾動幾圈？

生9：還是2圈，因為線段長度還是4πr.

追問1：有不同意見嗎？

生10：我認為不是2圈，感覺比2圈多一點.

追問2：為什么會多一點？

生10：在折點C處，圓多轉了一些.

師：請大家動手操作并思考能否得到滾動的具體圈數.

（學生動手操作）

（學生自發鼓掌）

師：精彩！一起看滾動的過程！（動畫展示滾動過程，如圖4）

追問3：有其他思路嗎？可以從圓心經過的路徑來解釋嗎？

生12：可以的，圓心經過的路徑是兩條線段加一條圓弧，兩條線段的長度一共是4πr，圓弧的半徑為r，圓心角為90°，弧長是，所以圓心經過的路徑長是.然后用圓心經過的路徑長除以圓周長，也可以得出圈.

師：這名同學的回答很精彩，說明這個問題既可以用角度去解決，又可以用圓心經過的路徑來解決.（學生自發鼓掌）

圖5

問題5：如圖5，將總長為4πr的線段AB在中點C處折成60°，此時這個半徑為r的圓從點A到點B需滾動幾圈？

師：還有其他思路嗎？

設計意圖：探究圓在折線上滾動的過程，在操作中感受折點處圓的運動，體會在折點處即圓的自轉與公轉的復合運動，以圓公轉的角度和圓心運動的路徑刻畫運動過程，由表及里，逐步發現解決問題的關鍵.

4.破解難點，極限思想轉化核心問題

圖6

問題6：如圖6，連接AB，此時這個半徑為r的圓沿△ABC的外側滾動1周需滾動幾圈？

師：你能分別從旋轉的角度和圓心運動的路徑來解釋嗎？

生15：圓在三角形三個頂點處做旋轉運動，加起來一共旋轉了360°，所以轉了1圈.圓心在三個頂點處的運動路徑合起來恰好是1個圓周，所以通過圓心經過路徑除以圓周長也是1圈.最終的答案是3圈加1圈，即4圈.

師：精彩！如果將特殊的三角形變為特殊的四邊形呢？

問題7：如圖7，將等邊三角形改為正方形，則這個圓沿正方形的外側滾動1周需滾動幾圈？

（學生略加思考后齊答：5圈）

師：繼續增加難度，如果將特殊的圖形換成一般的多邊形，結論還成立嗎？

圖7

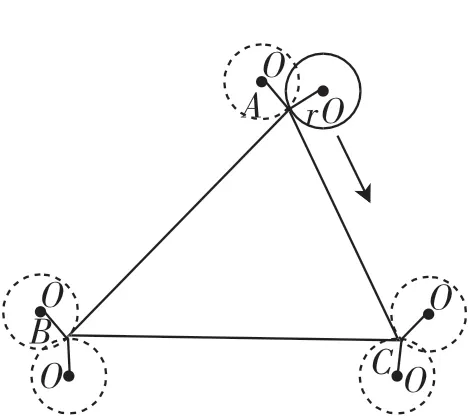
圖8

問題8：如圖8，將等邊三角形改為任意三角形，且該三角形的周長為a，則這個半徑為r的圓沿△ABC的外側滾動1周需滾動幾圈？獨立思考后小組討論.

（兩分鐘后，陸續有學生舉手）

師：為什么圓在三角形頂點處滾動的角度和為360°？

生16：頂點處滾動的角度與每個內角是互補關系，數值上等于外角，三角形的外角和是360°，所以圓在幾個頂點處滾動的角度之和為360°.

師：如果繼續將四邊形改為任意的多邊形呢？

師：你能否歸納出圓在多邊形的外側滾動的圈數如何計算？生16：圓滾動的圈數=+1.

師：你回答得很好，下面大家來一起回顧我們的探究過程.

問題9：若多邊形的周長為2π，滾動1周需滾動幾圈？

生：（齊）2圈.

師：如圖9，如果無限增加多邊形的邊數，此時多邊形將會接近于一個圓，讓半徑為r的圓沿著該圓外側滾動1周，滾動幾圈呢？

生：（齊）2圈.

圖9

設計意圖：層層遞進，探究圓在封閉的多邊形上滾動的過程，在操作中感知圓滾動的過程中變與不變的元素.在探究中發現問題的本質，從特殊到一般，在不斷增加邊數的過程中體會極限的數學思想.

5.回歸主線，交流中探尋原理

圖10

師：回到開始的問題，現在你能結合本節課所探究的經驗，解釋為什么硬幣滾動的是2圈嗎？

（動畫展示滾動過程，如圖10）

生：從旋轉角度來看，滾動的硬幣滾動了1個圓周長，同時也旋轉了1個圓周360°，所以是2圈.

生：從圓心經過的路徑長來看，圓心的路徑是一個半徑為2r的圓，路徑長為2π乘以2r等于4πr，用圓心經過的路徑長除以圓周長，即4πr除以2πr，結果為2圈.

設計意圖：回歸探究圓在圓周（曲線）上滾動的過程，首尾呼應，突破本節課的難點，在一系列問題的解決和探究中，讓學生感悟數學探究的魅力.

6.課堂小結，提煉核心思想

師：回顧解決問題的過程，你學到了哪些知識？有什么收獲？

生：研究圓的滾動，可以從兩個方向去探究，一個是圓在滾動過程中旋轉的角度，另一個是圓心經過的路徑長.

生：探究問題可以先易后難，從簡單出發，逐步深入探究復雜問題.

設計意圖：通過小結，梳理探究思想，總結探究活動中獲得的經驗，提煉核心思想，同時鍛煉學生的語言表達能力，培養學生勇于發表自己見解的能力.

二、教學思考

1.激發興趣，探究中積累活動經驗

《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）中明確提出，教師教學應該以學生的認知發展水平和已有的經驗為基礎，面向全體學生，注重啟發式和因材施教.教師要發揮主導作用，處理好講授與學生自主學習的關系，引導學生獨立思考、主動探索、合作交流，獲得基本的數學活動經驗.

為了激發學生的學習興趣，教師需要悉心準備和策劃合理的教學過程，設計的教學活動應以學生的數學認知規律為基礎，給學生提供更廣闊的探究空間.以本節課為例，教師以硬幣滾動的問題設計引入，學生提出猜想，發現操作結果與猜想不一致，激發了進一步探究的興趣.教師引導學生發現硬幣滾動問題本質上是圓的滾動，接著讓學生思考如何去探究這一問題.學生從圓在直線上的滾動開始，延伸到折線上的滾動，再到特殊多邊形乃至任意多邊形上的滾動，最終回歸到圓的滾動上，遵循了從特殊到一般的研究思路.

2.著力基礎，探究中把握知識生長

綜合與實踐活動課需要以學生課內知識為基礎進行生長.筆者認為基礎的知識點有兩處：一處是圖形的運動，學生對于圖形三種基本的運動方式已經非常熟悉，但是對于復合的運動方式尚且生疏；另一處是圓的相關知識，特別是點與圓的位置關系及直線與圓的位置關系等，為本節課的探究提供了有效的知識鋪墊.

課堂教學中，教師宜從這兩處入手.（1）從基本的圖形運動方式進行知識生長，可看作平移和旋轉的復合運動.當圓在直線上滾動時，可以看作“整體平移與局部旋轉的復合”，從整體看是整體的平移，從局部看是圓自身的旋轉；當圓在折線上滾動時，直線部分與前一種情形是一致的，學生探究的難點在于圓在折點處的運動.（2）從復合運動的角度進行知識生長，折點處圓的滾動可以看作“整體旋轉與局部旋轉的復合”，即折點處圓整體繞著折點做旋轉運動，同時自身也在轉動.同樣，圓在多邊形和曲線上的滾動都可以看作平移與旋轉的復合運動.

值得注意的是，教師在課堂上的關鍵環節需要放慢節奏，給予學生充分的操作和思考時間，學生探究的過程即是知識不斷聯系、重塑和發展的過程，更是知識生長的過程，教師要幫助學生把握好這一過程.

3.立足實踐，探究中提升數學素養

《標準》中還明確指出，數學是人類文化的重要組成部分，數學素養是現代社會每一個公民應該具備的基本素養.數學綜合與實踐活動的教學本質是思維的教學，綜合與實踐活動課應以操作和實驗作為基礎，引領學生的思維，通過課堂上的操作活動啟迪學生的思考.

課堂上教師不僅要關注學生掌握解決問題的方法，更要關注學生數學素養的提升.在本節課中，學生從具體的硬幣滾動中抽象出基本圖形即圓的滾動，積累了從具體到抽象的活動經驗，發展了學生數學抽象的能力.同時，學生從已有的知識和經驗出發，有目的地探索圓在不同圖形上滾動的過程，在不斷深入的探究和思考中，學生進一步發展了幾何直觀和空間想象的能力.整節課，通過師生間的共同探究，讓學生經歷知識的發生過程，從而獲得數學活動經驗，進而讓綜合與實踐活動成為提升學生數學學科核心素養的載體.