基于風致振動機理的壓電發電機實驗及仿真研究

陸油松 張大有 趙悄然 隋 麗

(1.北京理工大學，北京100081；2.北京航天計量測試技術研究所，北京100076)

1 引言

隨著低功耗微機電系統的發展，涌現出許多微型發電裝置為低功耗設備供電，其中壓電發電機就是典型的代表。壓電材料和壓電俘能器具有廣泛的應用前景和巨大的開發潛力，但是基于現有技術的局限性，壓電發電機僅適用于耗電量較小的小功率設備。為研究影響壓電發電機發電性能的參數，提高壓電發電機的能量輸出特性，研究人員對壓電發電機的俘能機理、結構優化等方面進行了理論、仿真和實驗等方面的研究。

Chen，Wang 和 Chien(2006)[2]推導了雙壓電晶片在正弦激勵下的發電性能，同時設計實驗驗證了理論研究的正確性，其理論推導得到的最大電壓值與實驗得到的最大電壓值較為接近。單小彪，袁江波，謝濤等(2010)[1]和王浩金，鄔丹燕，肖金等(2011)[3]等對單晶壓電梁進行了數學建模和仿真。Kundu和 Nemade(2016)[4]對雙晶壓電梁進行了數學建模和仿真。闞君武，唐可洪，王淑云等(2008)[5]分別對單晶壓電梁和雙晶壓電梁進行了數學建模和仿真。Stanton，Erturk，Mann等(2010)[6，7]研究了壓電材料非線性對壓電俘能器動態力學的影響。Doar，Eacute 和 Michelin(2011)[8]研究了風致振動壓電俘能器的線性穩定問題和轉換效率。Zhao，Liu，Wang 等(2017)[9]研究了低頻擾動條件下壓電俘能器的能量收集性能。Yee，Radeef，Chao等(2017)[10]研究了俘能器結構動力學對其俘能效果的影響。Abdelmoula和 Abdelkefi(2016)[11]研究了阻抗對基于馳振的能量收集系統俘能效果的影響。Hong，Sui，Zhang 等(2018)[12]對復合壓電懸臂梁中性面對其俘能效果的影響進行了研究。

針對微機電系統及微型壓電發電機的發展現狀，本文對一種基于風致振動機理的柔性壓電懸臂梁進行了實驗及仿真研究。致力于探究柔性懸臂梁的顫振機理及其在不同流速環境中的電壓輸出特性，同時研究在二階顫振條件下單個壓電懸臂梁給電容充電的充電性能，為建立風致壓電發電機模型提供仿真依據。

2 壓電柔性懸臂梁顫振機理仿真

壓電柔性懸臂梁是壓電發電機的能量轉換元件，其在風場中的振動是一個復雜的受力過程。為提高壓電發電機的輸出性能，需對壓電柔性梁與流場的流固耦合模型進行研究，懸臂梁與安裝夾具的流固耦合示意圖如圖1所示。

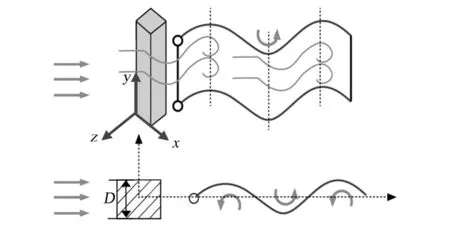
圖1 柔性梁在風場中的振動示意圖Fig.1 Vibration diagram of flexible beam in wind field

2.1 柔性梁在風場中的顫振分析

為探究壓電柔性懸臂梁在流場中的顫振機理，本文采用COMSOL軟件對壓電懸臂梁進行流固耦合仿真。壓電懸臂梁模型由一層壓電材料(PVDF)和一層304不銹鋼基底材料構成，其幾何尺寸和材料參數如表1所示，有限元模型如圖2所示，圖中方塊為模擬壓電懸臂梁的夾具，后方的黑色直線是壓電懸臂梁的側視效果。

圖2 流固耦合仿真模型Fig.2 Fluid-Structure-Interaction simulation model

表1 壓電懸臂梁的模型參數Tab.1 Model parameters of piezoelectric cantilever

由于有限元算法的要求，風場加載是一個帶有一定斜率的階躍加載過程，即將目標風速乘一個階躍函數，函數在不同時間所對應的的值為與目標風速相乘的系數。階躍函數曲線如圖3所示，調節階躍函數的斜率可以改變加載時間，這樣避免了直接加載目標風速造成的不收斂。

圖3 階躍函數曲線Fig.3 Step function curve

柔性懸臂梁在風場中的狀態由靜止到規律振動的風速叫做臨界風速，臨界風速是壓電懸臂梁振動系統的重要參數。當風速大于臨界風速時，柔性梁的自激振蕩可以維持；風速低于臨界風速時，振動則慢慢衰減，逐漸趨于靜止。在設計過程中，應根據實際風速環境設計壓電懸臂梁的結構參數。圖4是表1所列壓電懸臂梁在風速為20m/s的風場中的自由端位移特性曲線。從圖中可以看出，當風速較低時，柔性梁做低頻振動，振幅較小；當風速高于臨界風速后，柔性梁做大幅值周期振動。由圖4可知，當時間t＞0.6s后，壓電懸臂梁發生顫振，對應于階躍函數曲線可知壓電柔性懸臂梁的顫振臨界速度約為15m/s。

2.2 柔性梁在風場中發生顫振時的力學環境

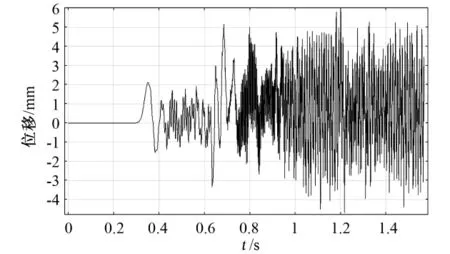
圖4 壓電懸臂梁振動時自由端位移特性曲線Fig.4 Displacement distributions of trailing edge when flutter occurs

壓電柔性懸臂梁在風場中的振動是一個復雜的受力過程，從圖5中可以看出，由鈍體阻擋產生的渦街沿著柔性梁長度方向交替分布，導致柔性梁上壓強較大的點不是單一的，造成柔性梁多個受力點同時作用，這些交變力使壓電懸臂梁往復振動。

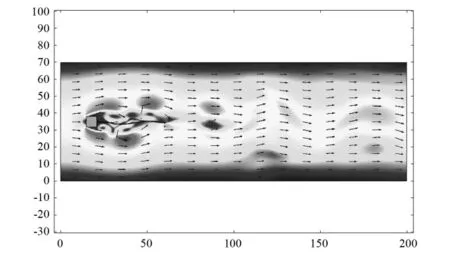
圖5 柔性梁周圍的渦街分布Fig.5 Vortex distribution around pizoelectric beam

3 壓電發電機輸出性能實驗

通過對壓電懸臂梁的流固耦合分析，對其在風場中的振動特性有了初步了解。為驗證壓電發電機在不同風速環境下的發電性能，本文將對單層壓電懸臂梁的輸出特性及充電性能進行測試。懸臂梁的尺寸為：長50mm，寬10mm，PVDF厚度0.03mm，基底厚度0.02mm。

3.1 實驗設計

為檢測壓電發電機在風場中的發電性能，按照如圖6所示的實驗方案搭建了測試平臺，用于模擬柔性梁和流場的流固耦合模型。本文采用鼓風機進行風速加載，整個測試平臺由鼓風機、風速儀、直流穩壓電源、示波器等組成。

圖6 總體實驗方案Fig.6 Schematic of experimental scheme

測試平臺實物圖如圖7所示。鼓風機的型號為“HAOBANG HB9026”、額定電壓為220V、風速范圍為(0～50)m/s，可以手動控制風速大小，也可以將風速固定在某一恒定值。風場范圍可通過改變套在鼓風機口的套筒直徑進行調節，套筒直徑越小能夠達到的風速則越高。穩壓源的作用是給風速儀提供穩定的直流電壓，型號為“XD1722”、電壓范圍為(0～30)V。

圖7 鼓風機加載實驗系統Fig.7 Diagram of Experimental setup

風速由型號為“KIMO CP 200”的風速儀測量，它由皮托管和變送器兩部分組成。法國KIMO公司的TPL-03-300型皮托管外徑為3mm，總壓孔直徑僅為1mm，適合應用于微小型器件內的流體速度測量。變送器使用法國KIMO公司的CP-202型號，風速測量范圍為(3～100)m/s；分辨率為0.1m/s。實驗時，將風速儀的風速輸入口放在鼓風機吹風口處，當風速大于懸臂梁的臨界風速時，懸臂梁發生大振幅的顫振，壓電材料將振動能轉換為電能，通過引出電極連接到示波器，來觀測壓電懸臂梁的輸出電壓及波形。

3.2 壓電發電機開路電壓實驗結果

壓電懸臂梁在低風速下的振動情況及輸出電壓信號如圖8所示。由高速攝影機拍攝到的圖像可知，在達到臨界風速前，壓電懸臂梁在風場中只有很小幅度的顫動，整體處于穩定狀態，輸出電壓幾乎為零。

圖8 低于臨界風速時壓電懸臂梁的振動及輸出電壓Fig.8 Vibration mode(a)and output voltage(b)of piezoelectric cantilever under the conditions of subcritical flutter velocity

當風速持續增加并超過一定值時，壓電懸臂梁開始大幅值振動，振型及輸出電壓如圖9所示，對比懸臂梁振動陣型可知，懸臂梁的振動姿態屬于二階振動。懸臂梁起振時的風速即為顫振風速或臨界風速。壓電懸臂梁的輸出波形是規律的近似正弦波的交流信號，且峰值較高，圖中所示為20V。

圖9 達到臨界風速后壓電懸臂梁的振動及輸出電壓Fig.9 Vibration mode(a)and output voltage(b)of piezoelectric cantilever under the conditions of supercritical flutter velocity

令風速從低到高增長，記錄壓電懸臂梁在不同風速下的輸出電壓值，繪制風速-電壓曲線如圖10所示。由圖可知，當風速由0增加到15.2m/s(臨界風速)的過程中壓電懸臂梁的輸出幾乎為零，當風速超過15.2m/s時輸出電壓突然增加，呈階躍變化。這是因為在此風速下，系統的凈阻尼變為負值，系統由穩定變為非穩定狀態，產生大幅自激振動。隨著風速繼續增大，振動系統能夠從外界汲取更多的能量用于維持自身振動，壓電懸臂梁仍保持著較高的電壓輸出且保持上升的趨勢。當風速增加到一定程度時，柔性梁的規律振動將被破壞，振型隨之變得混亂，同時輸出電壓的波形變為鋸齒狀。雖然此時輸出電壓的幅值依然較大，甚至在某些位置出現很大的峰值，但是這種振動情況要避免。一方面因為這種振動模態下壓電懸臂梁受到的力不規律，易造成柔性梁損壞；另一方面是因為過于混亂的波形會給后續的電源管理電路的器件選擇和最終電能存儲造成困難。

3.3 壓電發電機為電容充電實驗結果

通過上述實驗可知，壓電懸臂梁在一定的風速范圍內能夠有規律地振動，且輸出高幅值的交流電壓。如圖9(b)所示，壓電懸臂梁由于振動所產生的電壓是交流信號，不能直接給引信電路供電，需要將信號進行整流變換為直流電。另一方面，盡管壓電懸臂梁的輸出電壓相對較高，但電流極小，能量微弱，因此在使用時，需將壓電懸臂梁輸出的電能轉化為直流信號后存儲于儲能電容中，再在控制信號的激發下完成供電，流程如圖11所示。

圖10 電壓-風速曲線Fig.10 Voltage-Velocity curve

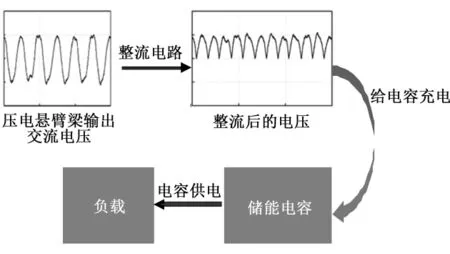
圖11 儲能流程圖Fig.11 Energy storage diagram

上述流程由電源管理電路來完成，本文選擇結構最簡單的標準電源管理電路，如圖12所示。

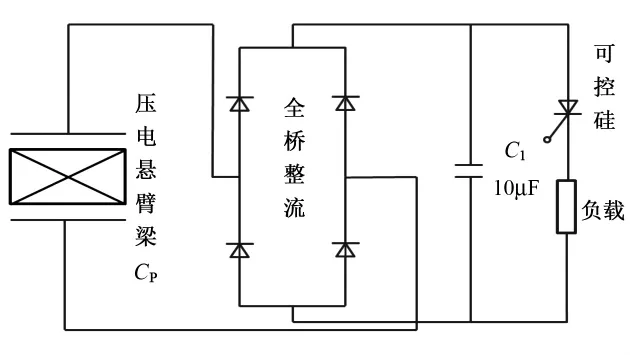
圖12 標準電源管理電路原理圖Fig.12 A standard energy harvesting circuit

在圖12所示的電路中，壓電懸臂梁的輸出被視作電壓源，由于其內阻很大，可將它等效為一個電容CP。壓電懸臂梁產生的交流電壓經過全橋整流，輸出脈動直流電壓，直流電壓再向能量存儲電容C1不斷充電。當可控硅的控制極為低電平時，負載開路，壓電懸臂梁產生的電荷被完全儲存在電容中，不會產生泄露，充電電路的時間常數相當于充電電容C1乘上壓電懸臂梁的輸出阻抗。

電容的充電曲線如圖13所示。與理想的充電曲線相似，充電曲線能夠反映出壓電發電機的輸出功率穩定，從另一個側面反映出懸臂梁的振動平穩。5s后，電容充電為8V，10s后，電容充電為22V。

由電容能量公式：Pt=1/2CV2，計算電容的充電功率，可以知道5s時充電功率為0.64mW，10s時充電功率為2.42mW，電容充電的功率能夠滿足低功耗設備的供電要求。

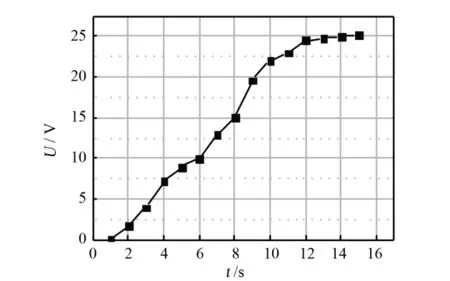
圖13 單壓電層懸臂梁給電容的充電曲線Fig.13 Charging curve with one singlepiezoelectric cantilever

4 結束語

本文通過對壓電柔性懸臂梁的流固耦合仿真以及發電性能的實驗探究，得出：

(1)柔性懸臂梁在流場中振動的原因是由懸臂上下面的交替壓強差引起的。當流速高于某一速度值時，柔性體會發生大幅度的振動，即顫振，該速度即為顫振臨界速度。

(2)當流速低于顫振臨界速度時，壓電懸臂梁的輸出幾乎為零。當流速達到顫振臨界速度時，壓電懸臂梁輸出電壓為類正弦曲線交流電，且峰-峰值較高。當風速增加到一定程度時，懸臂梁的規律振動將被破壞，振型隨之變得混亂，同時輸出電壓的波形變為鋸齒狀。

(3)單個壓電懸臂梁為10μF電容充電5s可達8V，充電功率為0.64mW，充電10s可達22V，充電功率為2.42mW。微型壓電發電機為低功耗微機電系統設備供電成為可能。