基于小波降噪的IMU精對準性能分析
張軒軒, 楊誠
(中國地質大學(北京) 土地科學技術學院,北京 100083)
0 引 言
捷聯式慣性導航系統(SINS)相對于平臺式慣性導航系統具有體積小、成本低等特點,已經廣泛應用于各種軍民導航領域. SINS通過加速度計和陀螺儀等慣性量測器件,測量載體的加速度和角速度[1]. 系統通過對載體加速度的積分獲得速度信息,再次對速度進行積分,獲得載體的位置增量信息. 然而,慣性導航系統需要事先獲取載體的初始狀態信息,包括載體的位置,速度和姿態,初始狀態的任何誤差都將無條件帶入后續的動態導航定位中. 初始狀態一般可以通過慣性導航的對準來實現. 慣性導航初始對準中的姿態對準是為了估計載體坐標系相對于參考坐標系的指向,并獲得載體坐標系到參考坐標系的旋轉矩陣. 該矩陣在導航過程中,將慣性傳感器量測到的比力和角速度從載體系投影到參考坐標系中. 因此,對準速度和精度決定了慣性導航系統后續導航精度.
捷聯式慣性導航傳感器的對準過程可以分為粗對準和精對準兩個部分. 粗對準一般采用解析的方法獲取姿態角的初始值,然后使用精對準對姿態角進行估計[2-4]. 由于慣性導航系統不依賴外界條件,可以通過自主量測的數據實現自主導航的系統,因此,對于高精度的慣性傳感器,可以通過自身量測數據感知地球重力與地球自轉,再通過卡爾曼濾波進行精對準,此過程稱為自對準[5]. 然而,對于中低精度的慣性傳感器,由于自身的噪聲較大,無法高精度地量測地球自轉,需要通過輔助的觀測信息進行精對準. El-Sheimy[6]提出利用多層小波分解法削弱傳感器量測數據的高頻噪聲. 該方法有效提高了對準精度和效率. 目前,精對準一般是基于慣性傳感器的小失準角線性誤差方程,通過卡爾曼濾波和慣性傳感器的小失準角線性誤差方程實現的[7]. 本文以高、中、低三種精度的捷聯式慣性傳感器為研究對象,利用卡爾曼濾波分析比較三種精度的慣性傳感器的精對準性能.
1 精對準及小波降噪原理
1.1 坐標系定義
SINS姿態對準的目的是為了獲取載體坐標系與參考坐標系之間的關系. 本文的載體坐標系(b)為右前上坐標系, 其原點位于慣性測量裝置(IMU)測量中心,x軸指向載體的右方,y軸指向載體運動的方向,z軸指向載體上方,構成右手坐標系. 為了討論問題方便, 一般令導航坐標系(n)與當地水平坐標系(l)重合; 另一個關注的坐標系是當地水平坐標系,該坐標系為東北天坐標系,其原點為運載體的中心,z軸向上指向天頂,x軸指向地理東向,y軸垂直于x軸與z軸構成的平面成右手坐標系.
(1)
式中,φ、θ、ψ分別表示橫滾角、俯仰角和航向角.
1.2 小失準角誤差模型
小失準角誤差模型是慣性導航系統的經典誤差模型,其核心是假設姿態誤差角為小角度. 因此,誤差方程可以通過在經典慣性導航力學編排的基礎上施加小的誤差擾動獲得[9],如式(2)~(4)所示.
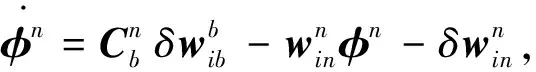
(2)
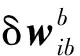
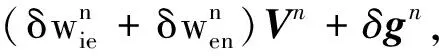
(3)
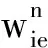
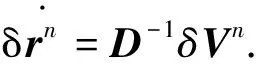
(4)
式中,D-1為位置誤差方程計算矩陣.
靜基座條件下,由于傳感器在靜止狀態下,νn=[0,0,0]T,理論上,位置分量誤差為零,因此式(4)可以省略.
因此,取導航坐標系為東北天坐標系時,慣性系統的狀態向量為[10]
Xk-1=[φE,φN,φU,δvE,δvN]T,
(5)
式中,δ(·)代表狀態的誤差,本文以δvE、δvN為觀測量.因此,卡爾曼濾波的離散化狀態模型為
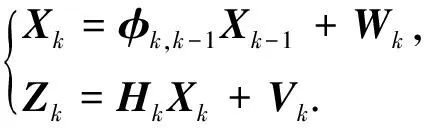
(6)
其中:
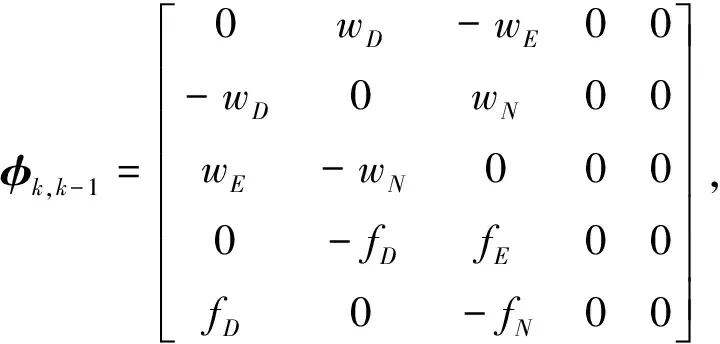
(7)
wN=ΩcosL+vE/R0,
(8)
wE=vN/R0,
(9)
wD=ΩsinL-vEtanL/R0,
(10)
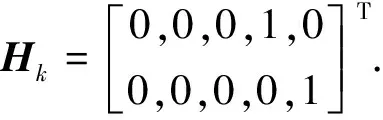
(11)
式中:φk,k-1為卡爾曼濾波的系數轉移矩陣;Xk-1為k-1時刻的卡爾曼濾波的狀態矢量;Xk為k時刻的卡爾曼濾波的狀態矢量;Wk為系統過程的噪聲向量;Hk為卡爾曼濾波觀測方程的系數矩陣;Vk為速度噪聲觀測向量;L為當地緯度;Ω為地球自轉角速率;R0為地球半徑.
1.3 小波降噪
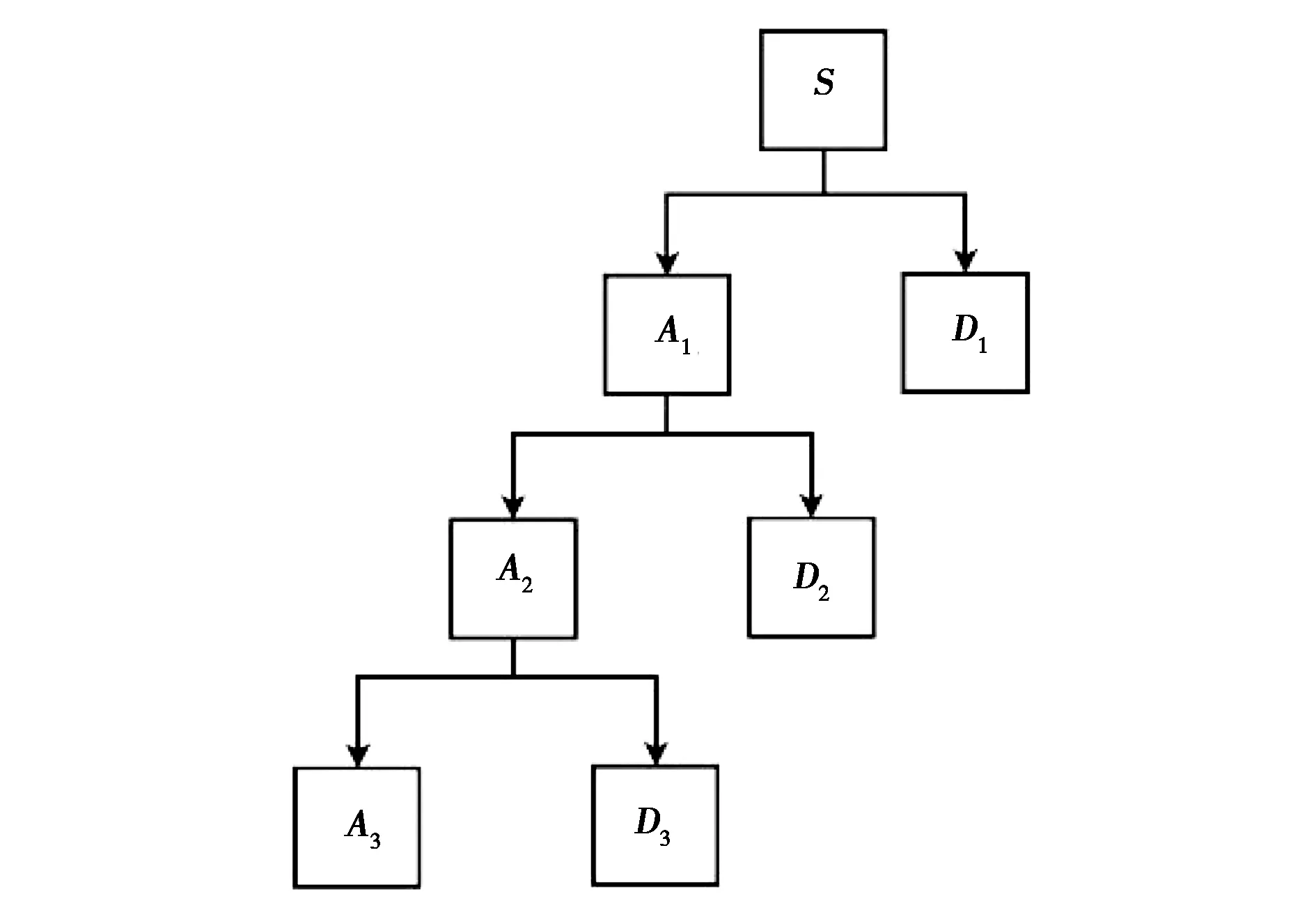
圖1 小波分解示意圖
2 仿真與實驗測試
為了對比分析高中低三種精度的慣性傳感器的對準精度,同時考慮到低精度慣性導航器件受外部噪聲影響較大,本文采用實測數據和低精度慣性器件仿真數據進行對準性能分析.實測數據由ATLANS、3DM-GX5-25和MPU-6700三種慣性傳感器采集,數據采樣頻率均為100 Hz. 三種傳感器的性能參數如表1所示. 同時使用相同參數生成MPU-6700仿真數據進行對比分析.
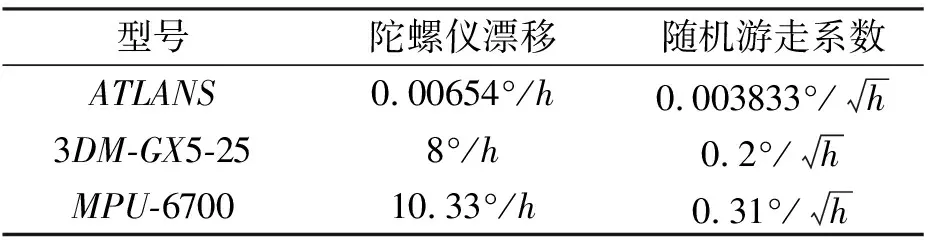
表1 傳感器參數
對于數據采樣時間通常是由對準所需的時間來決定的,而對準時間與對準所需達到的精度存在以下關系:
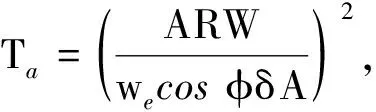
(12)
式中:ARW表示角度隨機游走;we為地球自轉角速度;φ為運載體所在的緯度;δA是方位對準誤差;Ta是對準時間. 本文所需要達到的方位對準誤差為0.01°/h,通過計算可知,ATLANS對準時間需要4 s,3DM-GX5-25對準時間需要10 903 s,MPU-6700對準時間需要24 532 s. 因此,數據采樣時長比對準時間長即可,本文采樣時長分別為:10 000 s,11 000 s, 500 000 s.對高頻噪聲,本文采用文獻[11]AB中的函數命令wden,選用db4小波基,分解層數為5. 經小波分析處理后,各個慣性器件的有效輸出信號均明顯降低,如圖2~5所示. 可以發現,MPU-6700去噪后的信號在0~500000 s間有明顯的非線性特征,這是仿真數據和另外兩種傳感器輸出的數據所沒有的.
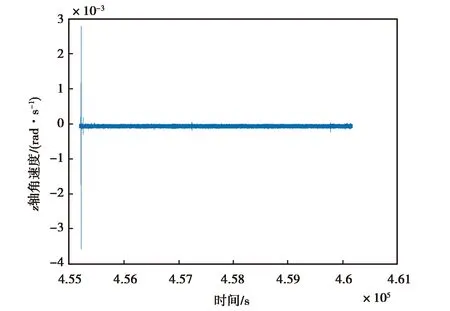
(a) ATLANS z軸角速度降噪前變化圖
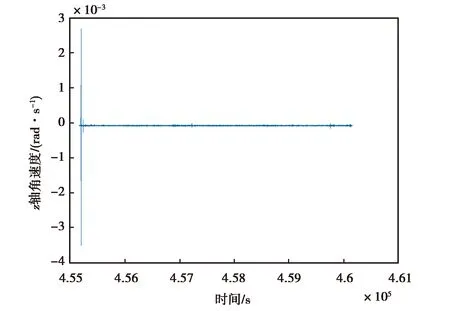
(b) ATLANS z軸角速度降噪前變化圖圖2 ATLANS z軸角速度降噪前后變化圖
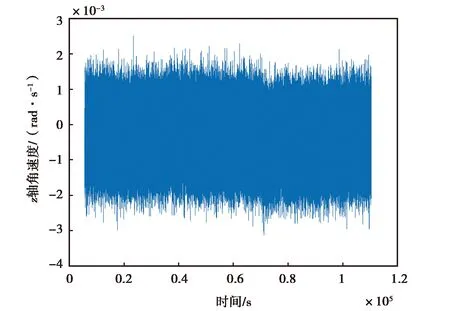
(a) 3DM-GX5-25 z軸角速度降噪前變化圖
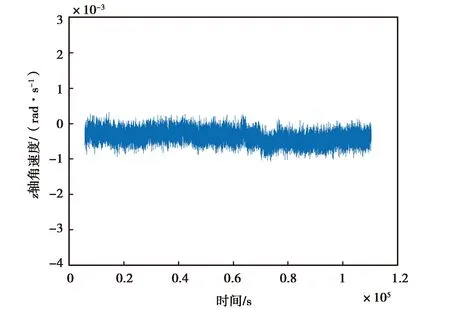
(b) 3DM-GX5-25 z軸角速度降噪后變化圖圖3 3DM-GX5-25 z軸角速度降噪前后變化圖
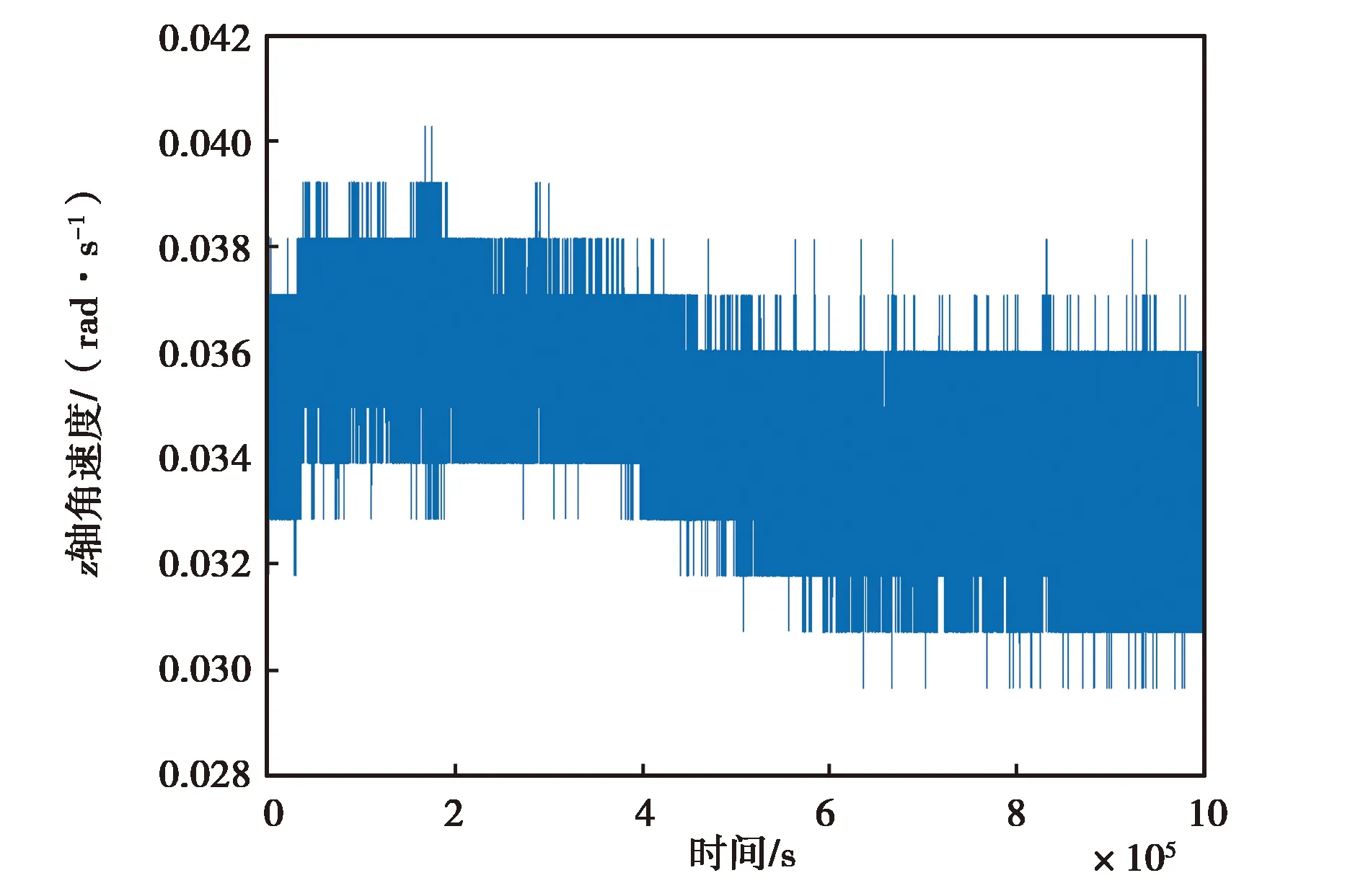
(a) MPU-6700 z軸角速度降噪前變化圖

(b) MPU-6700仿真z軸角速度降噪后變化圖圖5 MPU-6700仿真z軸角速度降噪前后變化圖
對3個慣性器件的實測數據與MPU-6700仿真數據進行功率譜分析,由于陀螺儀的精度對慣性導航的導航精度影響較大,本文選取各個慣性器件陀螺儀的z軸輸出角速度進行研究,各個數據的功率譜分析如圖6~9所示.
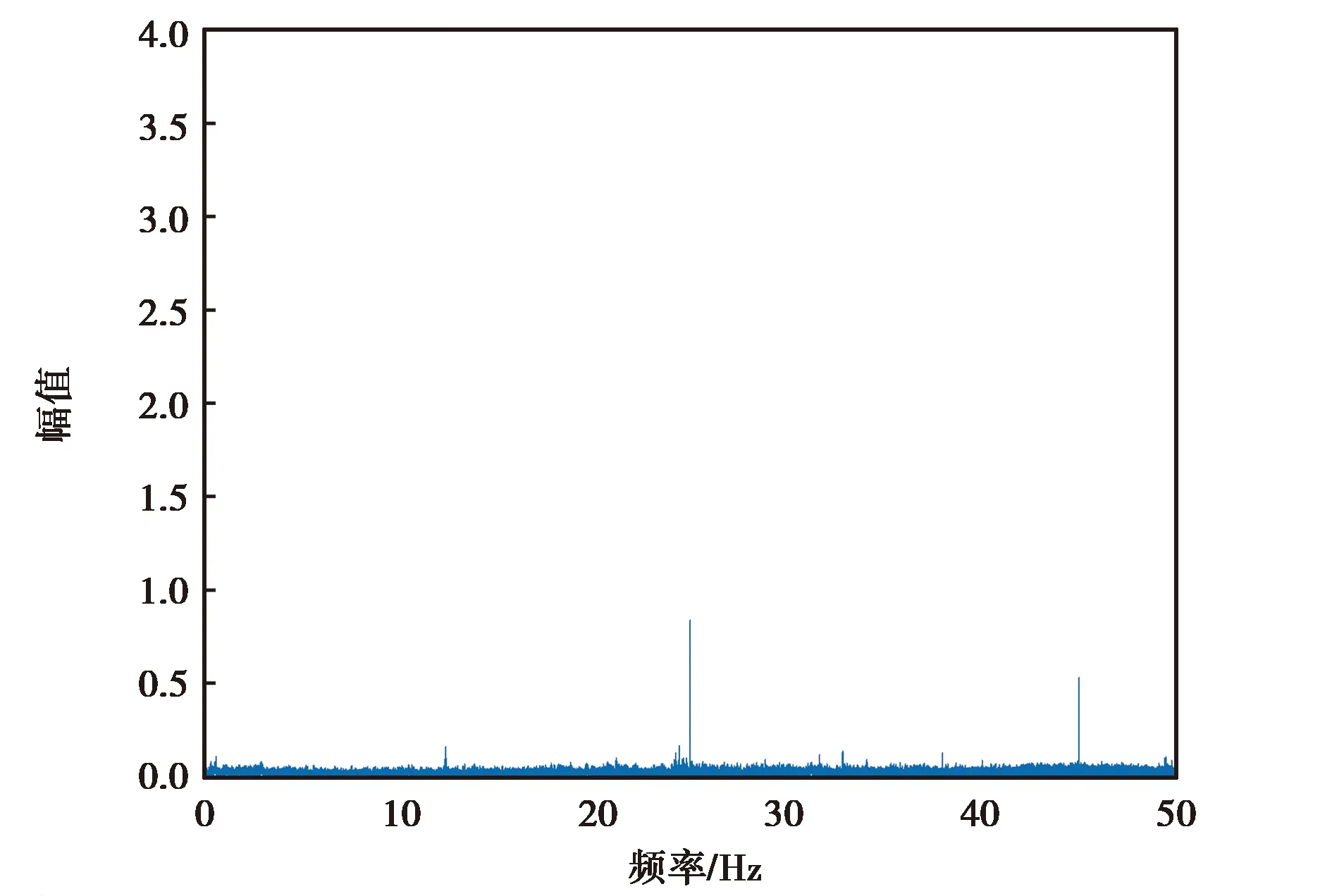
(a) ATLANS z軸角速度降噪前頻譜分析圖
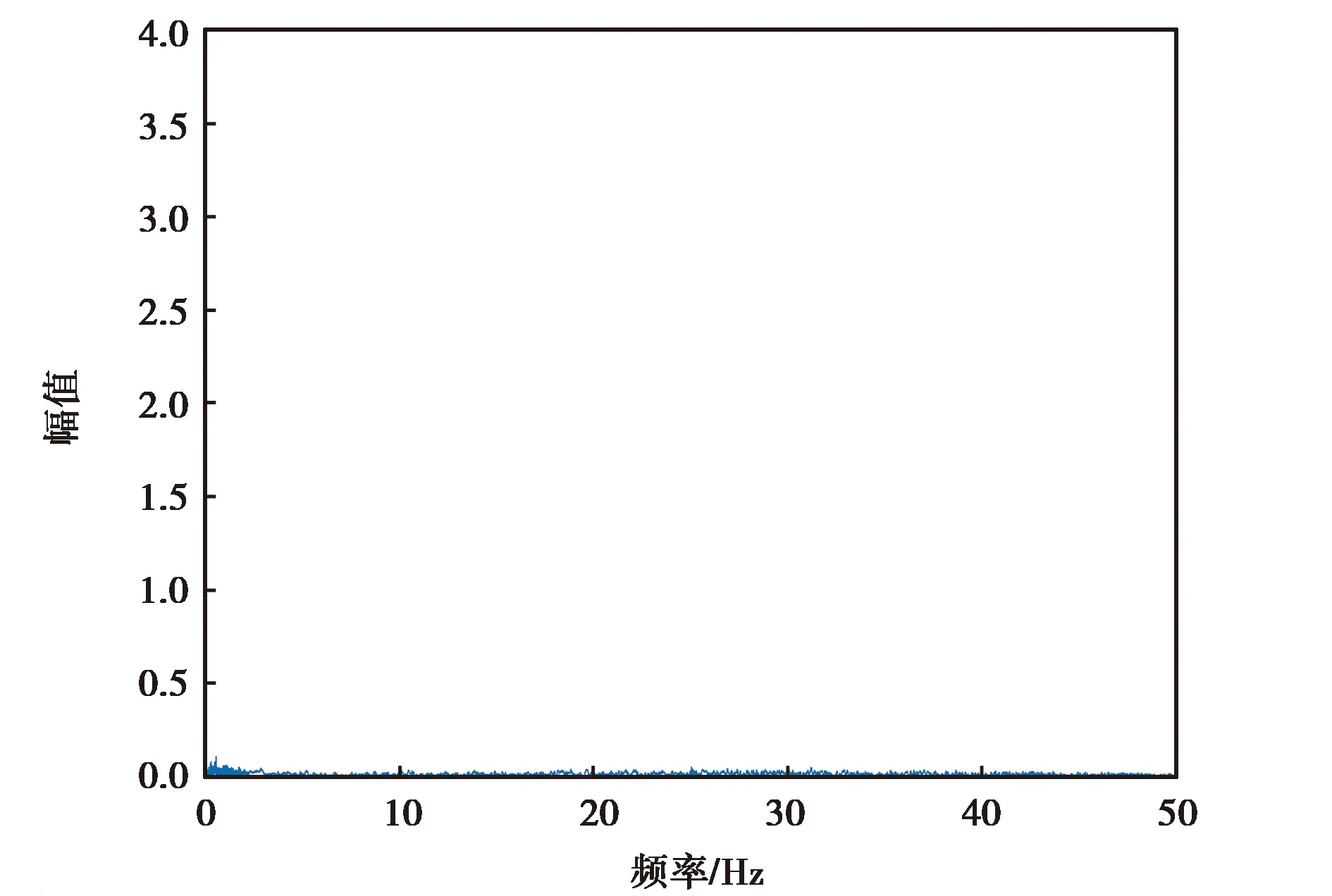
(b) ATLANS z軸角速度降噪后頻譜分析圖圖6 ATLANS z軸角速度降噪前后頻譜分析圖
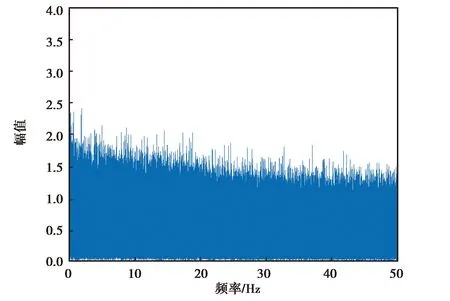
(a) 3DM-GX5-25 z軸角速度降噪前頻譜分析圖
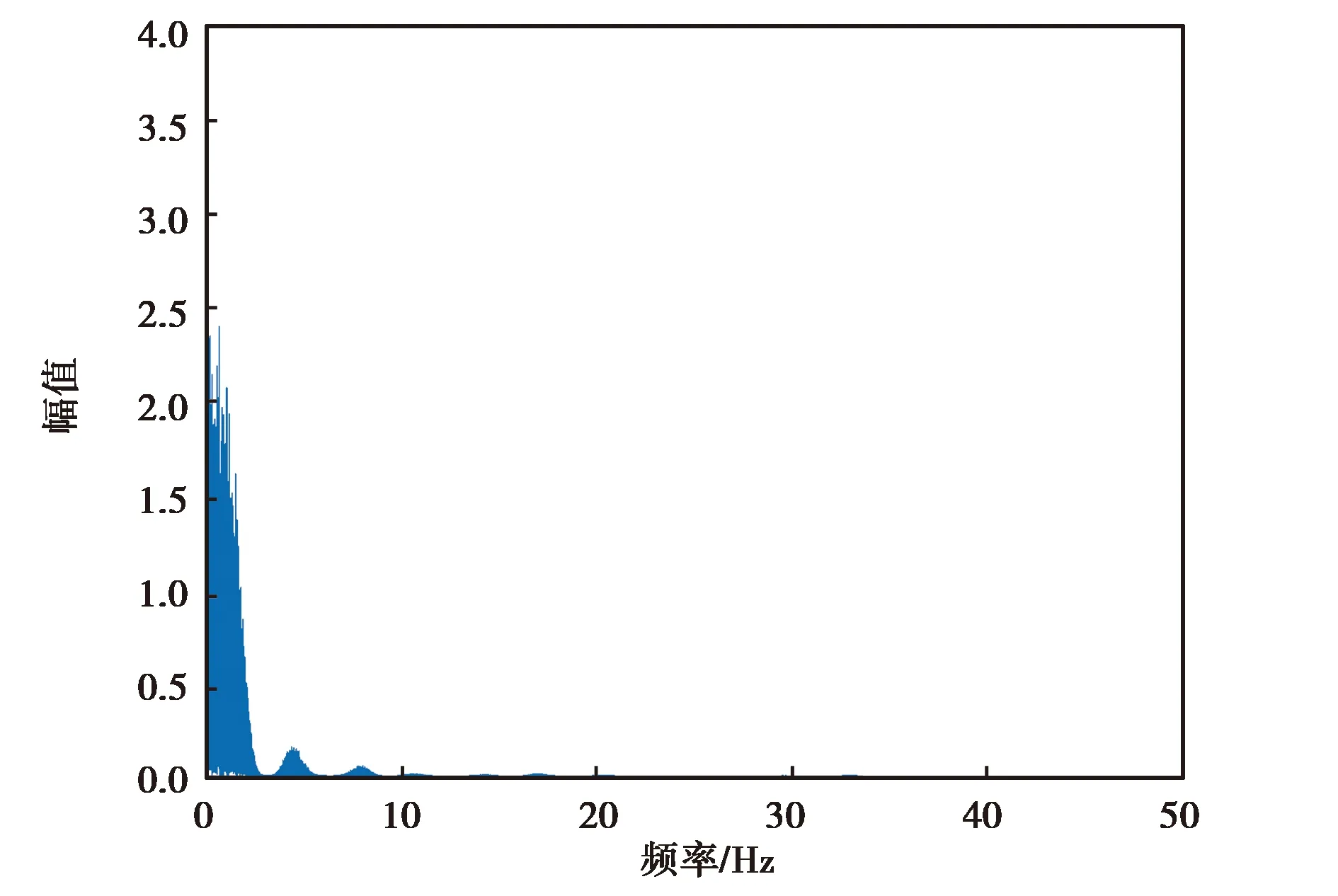
(b) 3DM-GX5-25 z軸角速度降噪后頻譜分析圖圖7 3DM-GX5-25 z軸角速度降噪前后頻譜分析圖
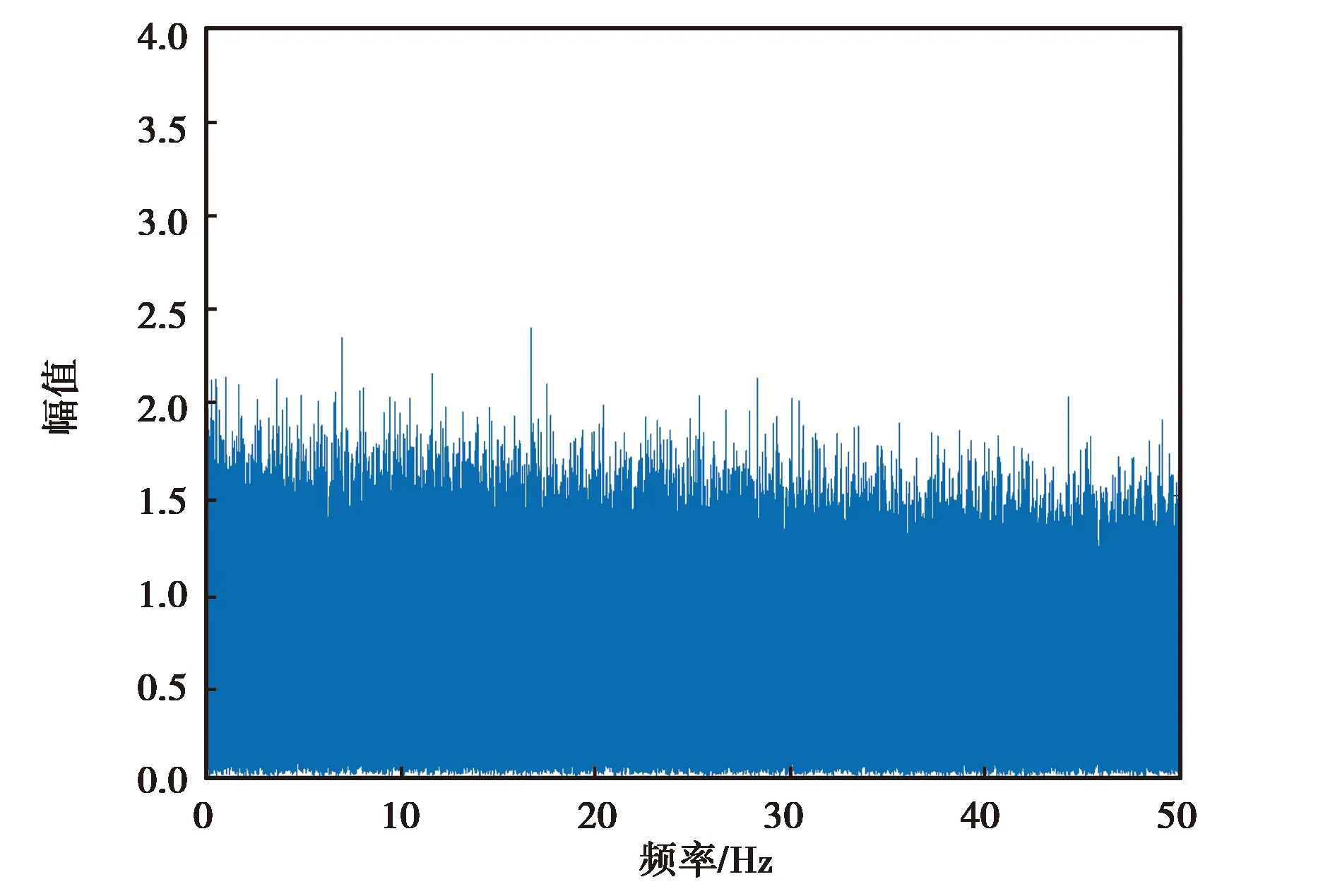
(a) MPU-6700 z軸角速度降噪前頻譜分析圖
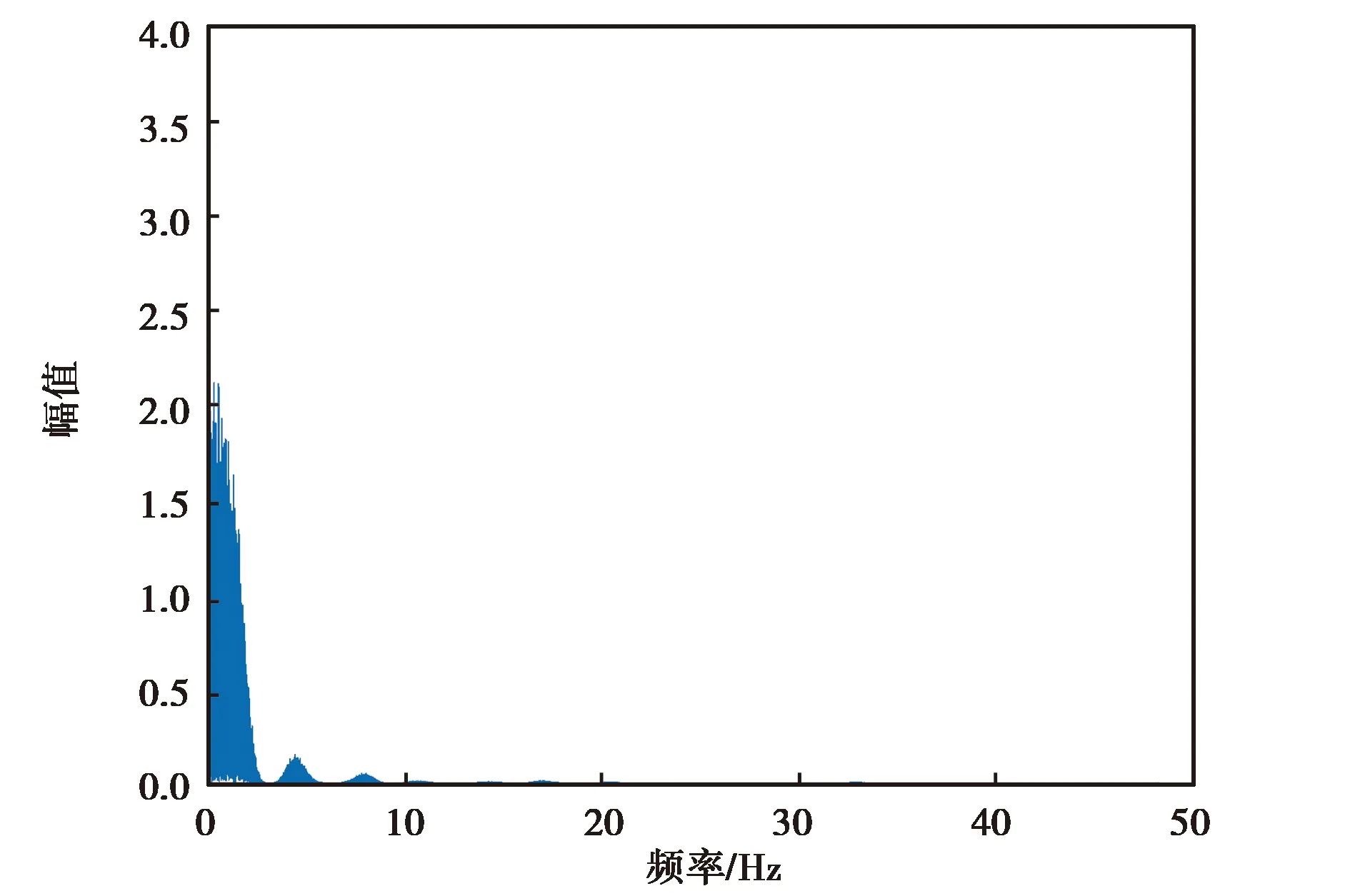
(b) MPU-6700 z軸角速度降噪后頻譜分析圖圖8 MPU-6700 z軸角速度降噪前后頻譜分析圖
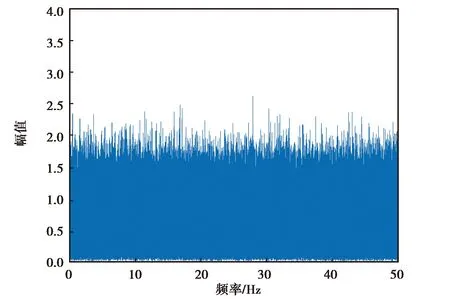
(a) MPU-6700仿真z軸角速度降噪前頻譜分析圖
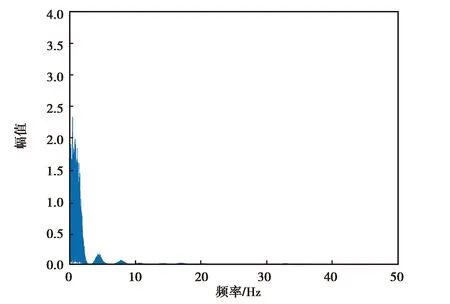
(b) MPU-6700仿真z角速度降噪后頻譜分析圖圖9 MPU-6700仿真z軸角速度降噪前后頻譜分析圖
由圖6~9可知,各個慣性器件在小波降噪前的高頻噪聲比較大,但經過小波分析處理,其高頻噪聲得到了有效抑制,保留了低頻有效信息.
數據經小波降噪后,通過粗對準獲取姿態角的初值,如表2所示.
一個完善的制度體系可以給管理者們起到良好的輔助作用,更可以讓員工約束其自身,促進工程進度,打消員工消極怠工的狀態,增強團隊的管理體系,完善制度從以下幾方面入手:

表2 粗對準姿態角
最后利用卡爾曼濾波精對準的方法進行姿態的解算,得到三種慣性器件姿態角隨時間的變化情況.進行卡爾曼濾波精對準時三種慣性器件的濾波初始狀態均為X=[10°,10°,10°,0°,0°]T,慣性器件ATLANS的狀態協方差矩陣為
P=diag((0.00625°/h)2,(0.00625°/h)2,(0.00625°/h)2,(100 μg)2,(100 μg)2),動力學模型噪聲矩陣為
Q=diag((0.009899°/h)2,(0.009899°/h)2,(0.009899°/h)2,(50 μg)2,(50 μg)2);
3DM-GX5-25狀態協方差矩陣為
P=diag((8°/h)2,(8°/h)2,(8°/h)2,(200 μg)2,(200 μg)2);
動力學模型噪聲矩陣為
Q=diag((1.2°/h)2,(1.2°/h)2,(1.2°/h)2,(180 μg)2,(180 μg)2);
慣性器件MPU-6700狀態協方差矩陣為
P=diag((10.33°/h)2,(10.33°/h)2,(10.33°/h)2,(3300 μg)2,(3300 μg)2);
動力學模型噪聲矩陣為
Q=diag((1.8°/h)2,(1.8°/h)2,(1.8°/h)2,(2880 μg)2,(2880 μg)2).
上述矩陣P和Q中前3項分別為各慣性器件陀螺儀的零偏和隨機誤差,后兩項為加速度計的零偏和隨機誤差.
仿真數據及實測數據的對準結果如圖10~13所示.
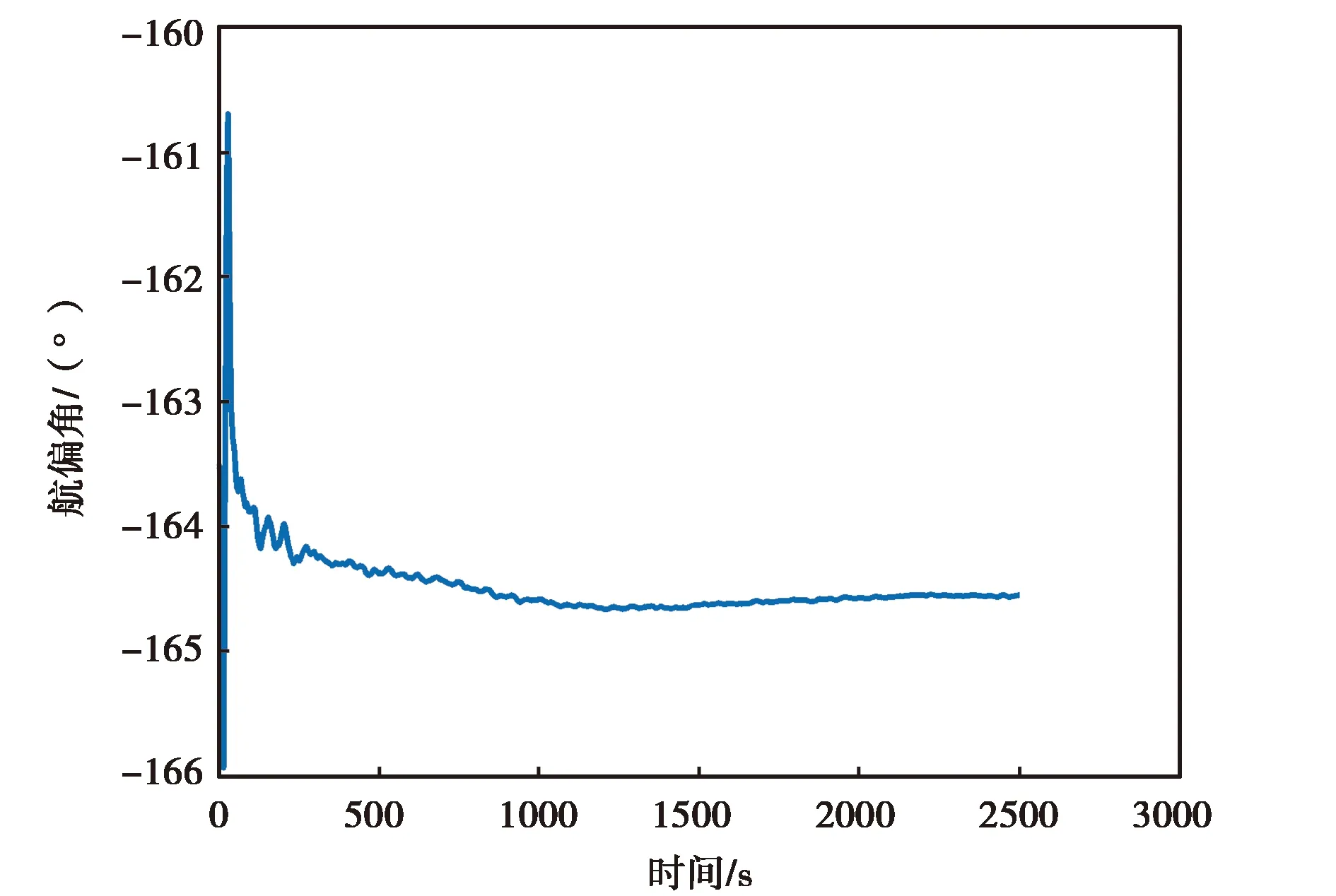
(a) ATLANS航偏角變化圖
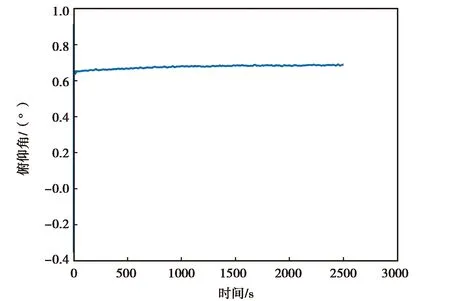
(b) ATLANS俯仰角變化圖
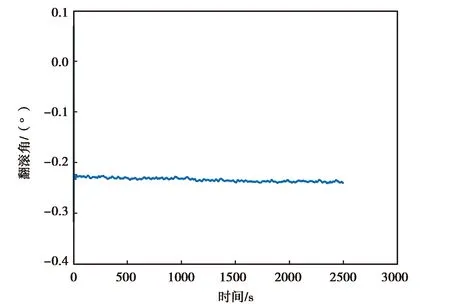
(c) ATLANS翻滾角變化圖圖10 ATLANS實測數據精對準結果圖
圖10示出的是ATLANS實測數據進行卡爾曼濾波精對準的姿態結果.由圖10(a)、(b)、(c)可知,ATLANS慣性器件的姿態角在最開始的時候是發散的,但是經過一段時間后開始收斂到固定的角度或固定角度附近,收斂的一致性比較好.
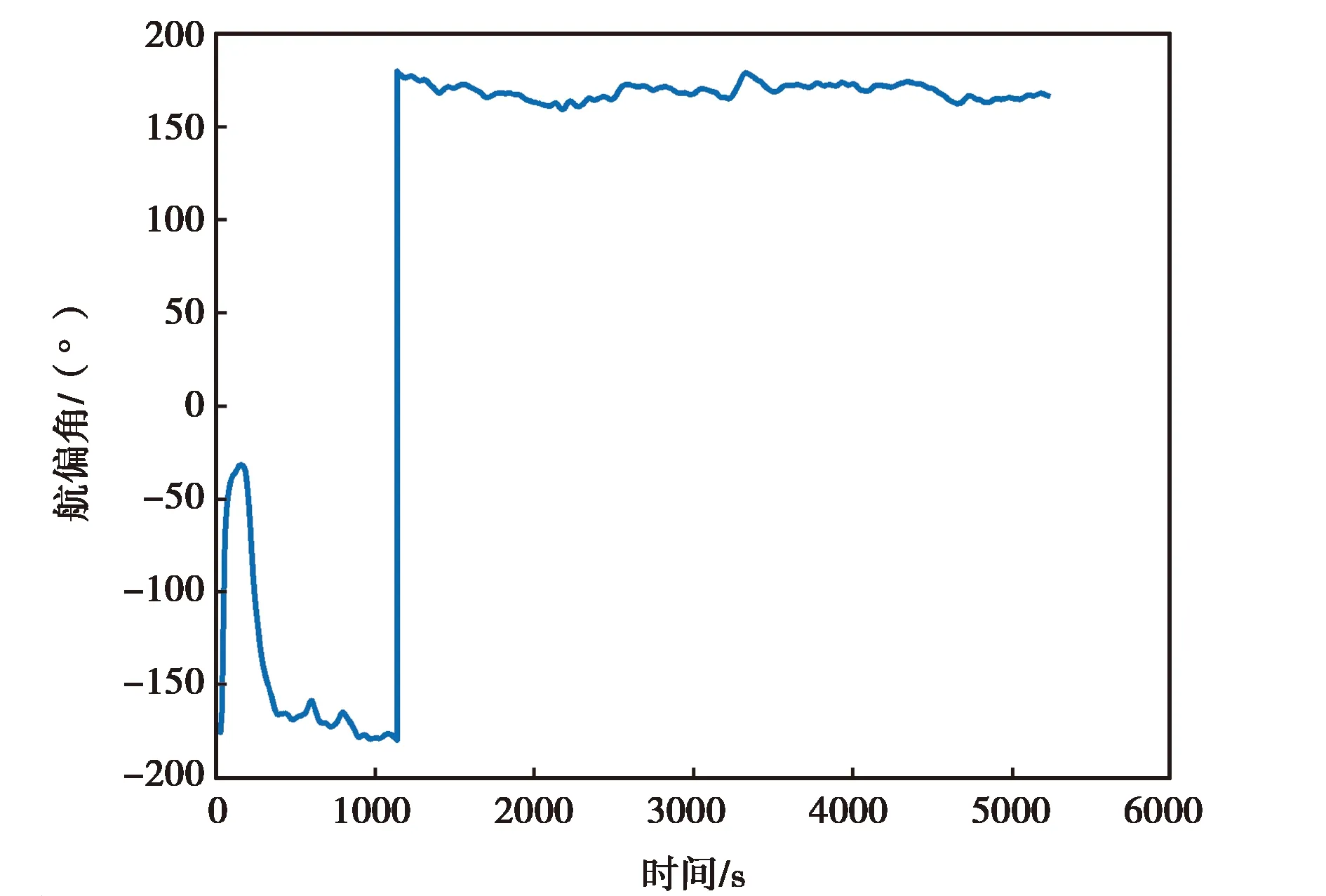
(a) 3DM-GX5-25航偏角變化圖
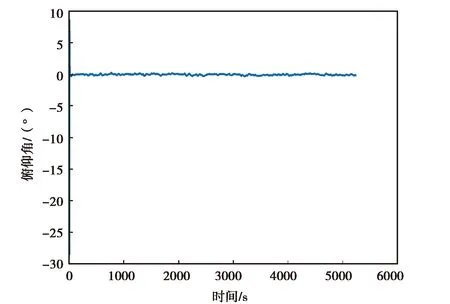
(b) 3DM-GX5-25俯仰角變化圖
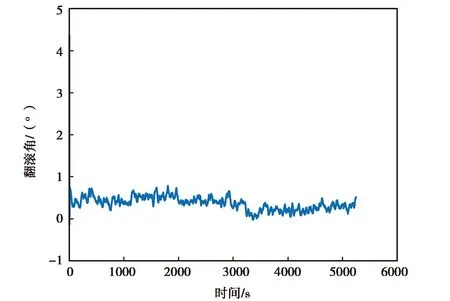
(c) 3DM-GX5-25翻滾角變化圖圖11 3DM-GX5-25實測數據精對準結果圖
圖11示出的是3DM-GX5-25實測數據和精對準的姿態結果,由圖11(a)、(b)、(c)可知,3DM-GX5-25慣性器件的姿態角最后均收斂到了一個固定角度或其附近,但可以明顯看到,其收斂速度慢,同時其翻滾角收斂時仍存在較ATLANS的翻滾角大的震動.

(a) MPU-6700航偏角變化圖
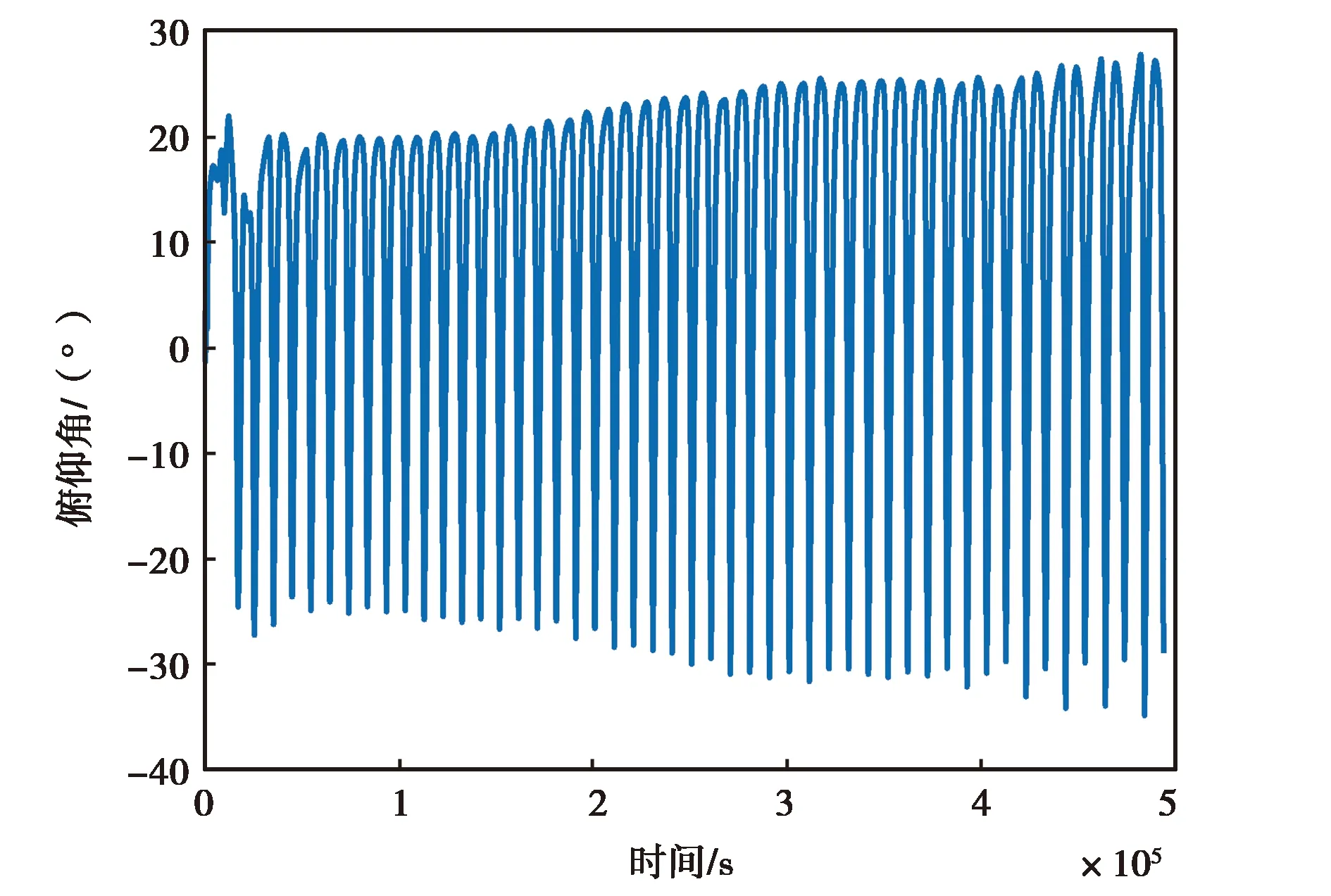
(b) MPU-6700俯仰角變化圖
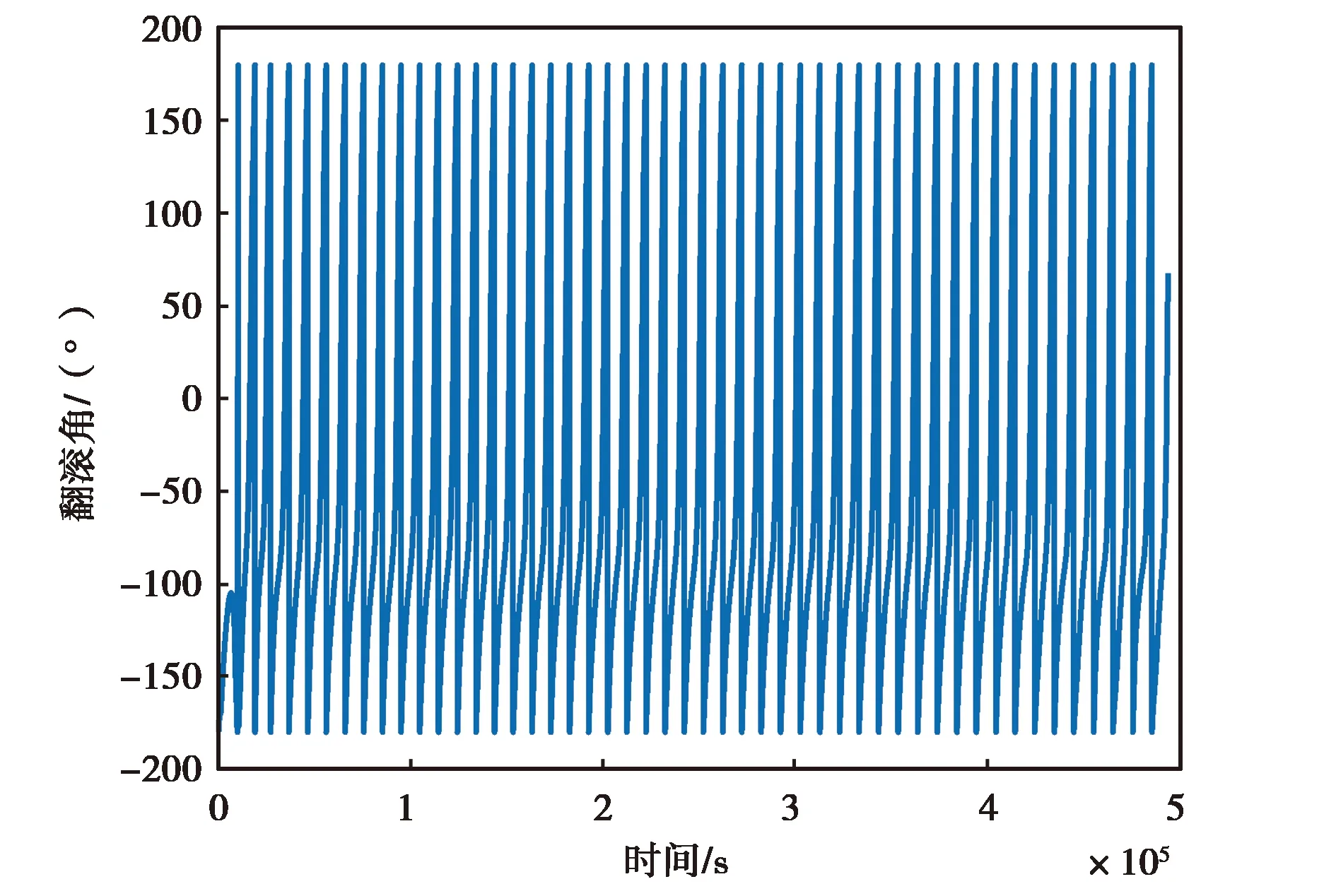
(c) MPU-6700翻滾角變化圖圖12 MPU-6700實測數據精對準結果圖
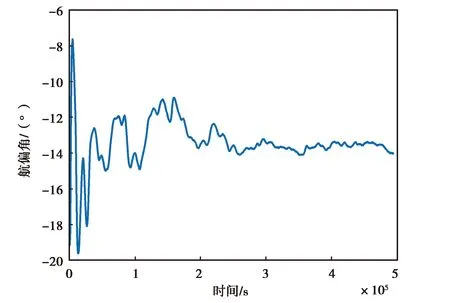
(a) MPU-6700仿真數據航偏角變化圖
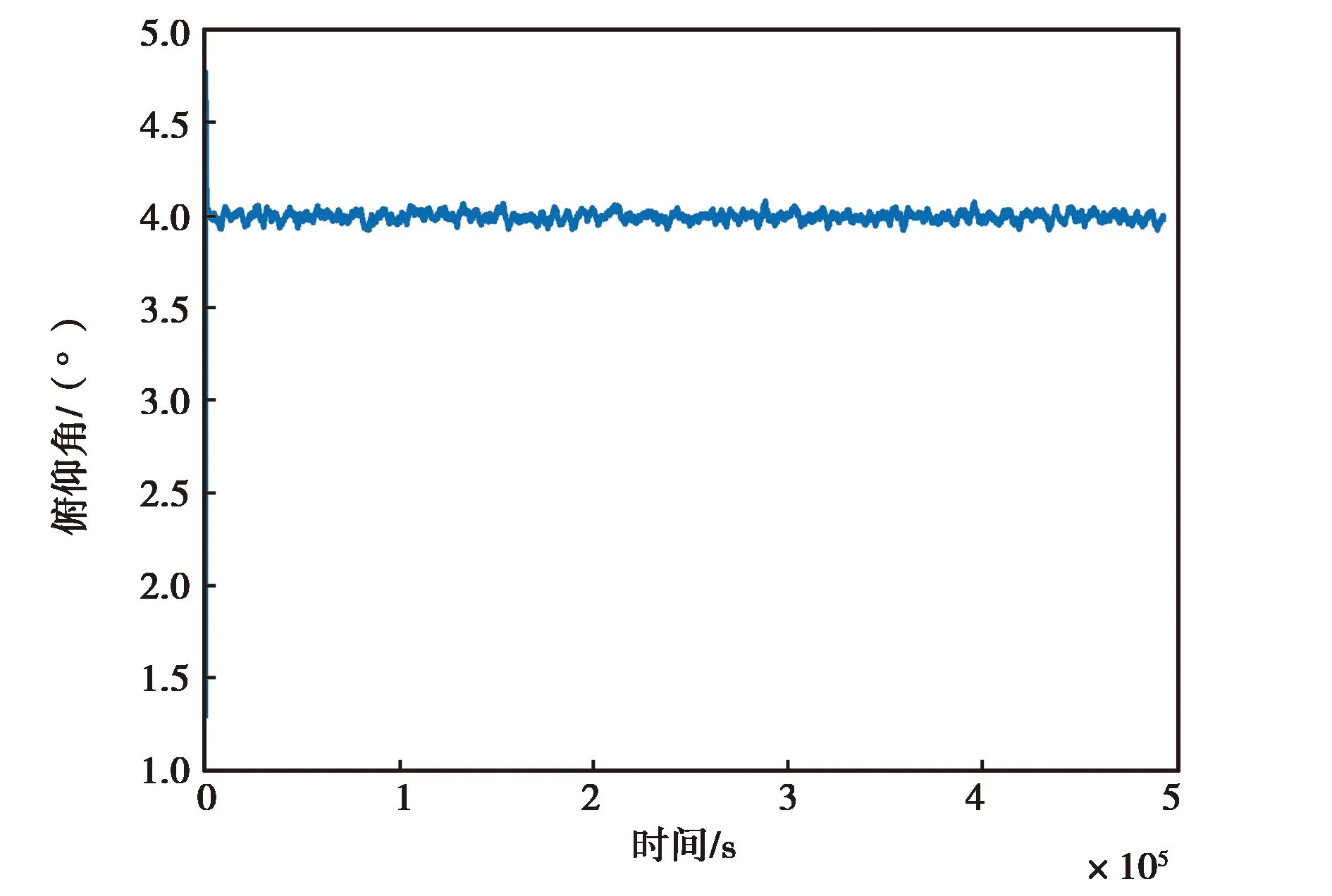
(b) MPU-6700仿真數據俯仰角變化圖

(c) MPU-6700仿真數據翻滾角變化圖圖13 MPU-6700仿真數據精對準結果圖
圖12和圖13示出的是MPU-6700實測數據和仿真數據的精對準結果圖,由圖12(a)、(b)、(c)可以直觀看出,MPU-6700慣性器件的三個姿態角隨時間的變化在不斷振蕩,最終無法收斂,而由圖13可以看出仿真數據能夠最終收斂于固定的角度附近.造成該現象的原因是低精度傳感器不僅僅受到白噪聲的影響,而且受其他復雜特性誤差的影響(如非線性誤差),其數據的低頻分量有著明顯的非線性特性. 而仿真數據受到的干擾單一,能夠快速收斂.
綜合圖10、11、12,由圖10(a),圖11(a),圖12(a)可以清楚地看到ATLANS的航偏角很快收斂到了一個固定角度的附近,3DM-GX5-25的航偏角則用了相對較長的時間才收斂,MPU-6700的航偏角則完全振蕩、發散;由圖10(b),圖11(b),圖12(b)可以看出ATLANS和3DM-GX5-25的俯仰角均較快收斂到了各自固定角度附近,而MPU-6700的航偏角則依舊振蕩、發散;由圖10(c),圖11(c),圖12(c)可以看出ATLANS和3DM-GX5-25的翻滾角均收斂到了各自固定角度附近,但3DM-GX5-25翻滾角的振蕩較ATLANS的翻滾角劇烈,MPU-6700的翻滾角則依舊振蕩、發散.
3 結束語
論文通過卡爾曼濾波對低、中、高三種不同性能的慣性導航器件進行基于以小波分析的精對準性能分析,最后對精對準結果的三個姿態角進行對比分析,得到如下結論:
1)小波分析方法可以有效抑制噪聲信號影響,提取出對精對準有用的信號,去噪效果明顯.
2)性能較好的慣性導航器件其精對準的速度較快,性能較差的慣性導航器件精對準的速度較慢.
3)性能高的慣性傳感器有著較好的對準精度;而低精度的傳感器,由于噪聲及誤差的原因,對準精度較低,甚至出現濾波發散情況.
4)性能較低的慣性傳感器由于受復雜特性誤差的影響無法對準,而采用相同噪聲參數仿真的數據可以實現較好的對準.

