直觀助思考 思辨破難題
——2017年新課標Ⅰ導數壓軸題剖析及啟示
孫 泰
(北京豐臺二中 100071)
導數大題是新課標卷的壓軸大作,教學中如何突破這道難關?現實中,歸類題型的“套路”派和借用高等數學公式、定理的“高觀點”派教學方式較為普遍,取得一定的效果,但都遇到了瓶頸,甚至埋下了隱患. 本文以2017年新課標Ⅰ導數題為例,談談自己的想法,與大家交流學習,旨為高三解題教學做一些探索.
1 試題呈現
已知函數f(x)=ae2x+(a-2)ex-x.
(Ⅰ)討論函數f(x)的單調性;
(Ⅱ)若f(x)有兩個零點,求a的取值范圍.
2 策略剖析
“對于任何學科的教學,最終都應當把培養學生的學科直觀作為重要的價值取向”[1],史寧中先生這段話指明了解題教學的重要方向,那就是解決數學問題始于直觀,終于理念.
策略1幾何直觀探方向,代數直觀妙解題
由(Ⅰ)當a≤0時,f(x)在區間(-∞,+∞)內單調遞減,從幾何直觀的角度分析函數圖象下降,不可能與x軸有兩個交點,所以函數f(x)不會存在兩個零點.
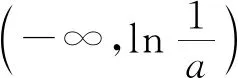
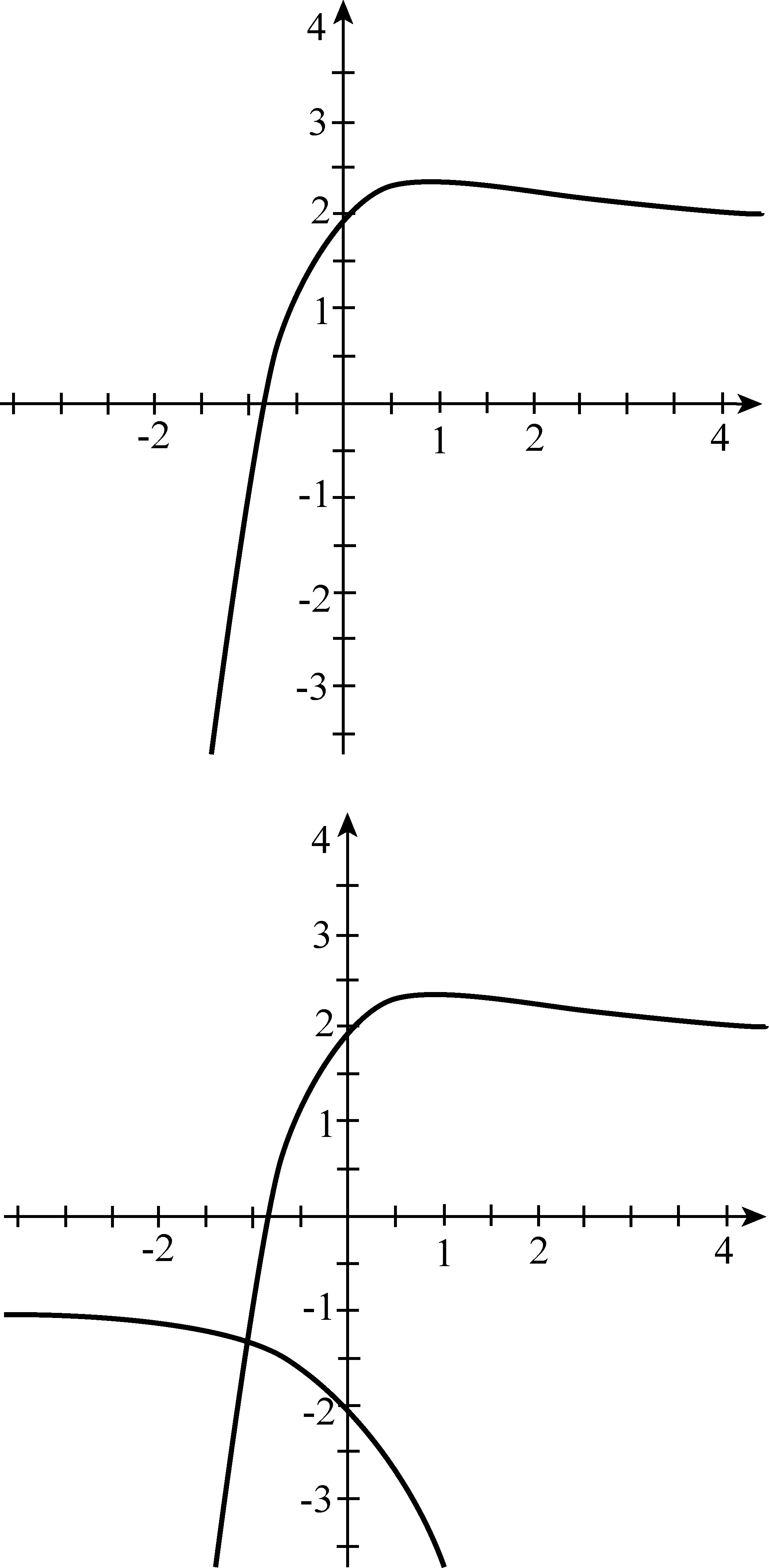
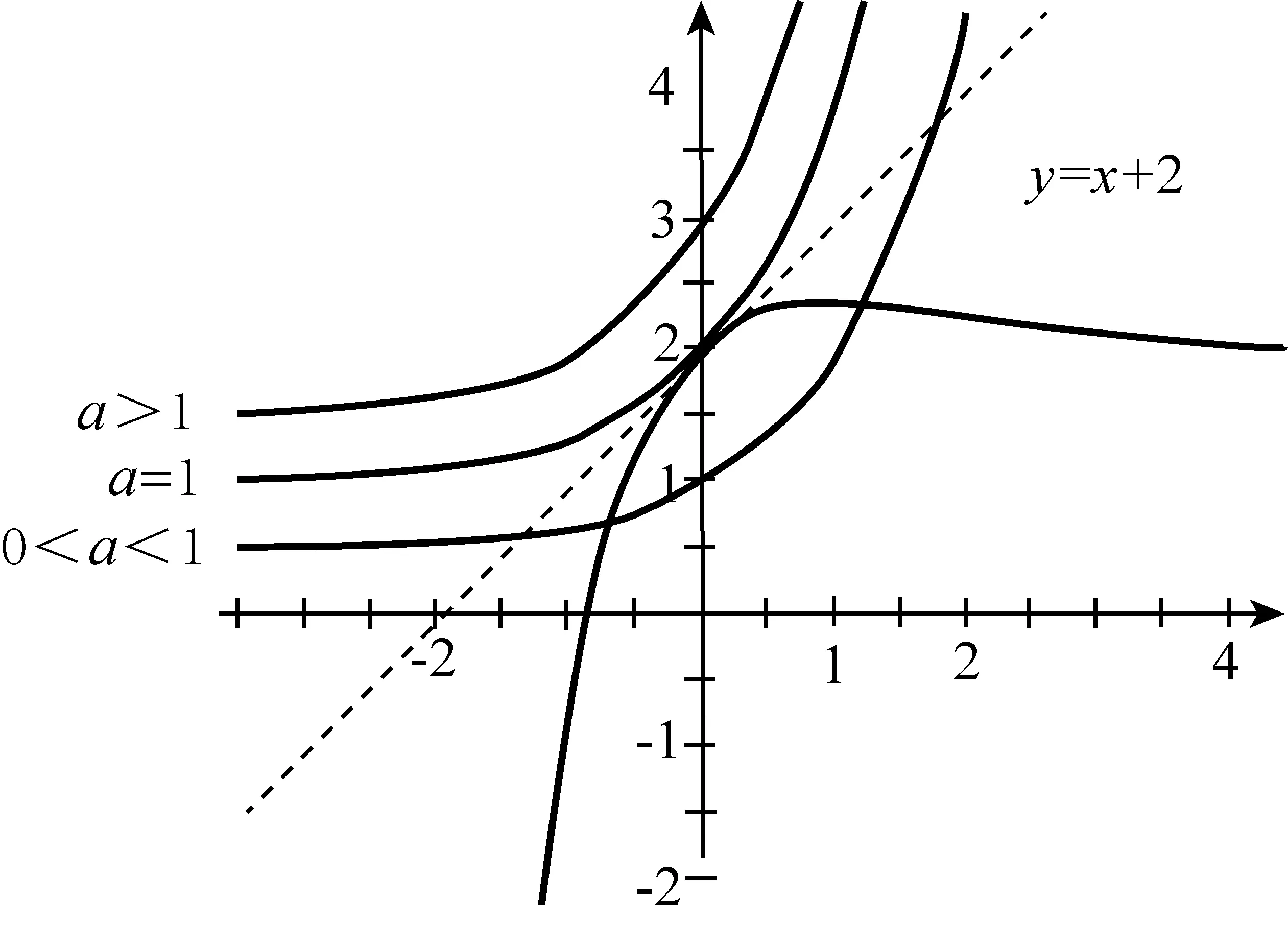
所以要使f(x)有兩個零點,必有0 分析f(x0)=ae2x0+(a-2)ex0-x0=ae2x0+aex0+(-2)ex0-x0,代數直觀,從組成解析式每部分的值的正負入手,其中含參數部分ae2x0+aex0>0,不含參數部分(-2)ex0<0,-x0>0,只需要找到超越不等式(-2)ex0-x0≥0的一個解,又0 直觀感知圖象趨勢,x→+∞時,ae2x→+∞,(a-2)ex→-∞,-x→-∞,不易判斷f(x)的符號,遇到困難. 如何找到呢? 代數直觀,簡化函數,難點在于函數解析式由超越指數函數和一次函數組合而成,不好處理,利用ex>x(x>0)放縮為可解方程,統一為超越形式 f(x0)=ae2x0+(a-2)ex0-x0 >ae2x0+(a-2)ex0-ex0 策略2代數直觀巧變換,幾何直觀助解題. f(x)=ae2x+(a-2)ex-x零點問題的代數變換方向有: 令h(x)=1-x-ex, 則h′(x)=-1-ex<0,又h(0)=0, 當x∈(-∞,0),h(x)>0; 當x∈(0,+∞),h(x)<0. 所以g(x)max=g(0)=1. 直觀感知圖象趨勢,x→-∞時,ex→0,x→-∞,因此g(x)→-∞;x→+∞時,e2x→+∞,ex→+∞,x→+∞,不能直接判斷,要么函數變形 h′(x)>0;當x∈(1,+∞),h′(x)<0, 分析函數g(x)=a(ex+1)的圖象,參數a的幾何意義是由函數y=ex+1到g(x)=a(ex+1)的伸縮變換系數. 如圖,當a=0時及a<0時,圖象直觀看得清楚,代數論證也不困難. 當a>0時,從幾何直觀開始. 當0 先證明函數g(x)與h(x)圖象在(-∞,0)上有一個交點. 至此得到函數g(x)與h(x)圖象在(-∞,0)上有一個交點.嚴謹嗎?正確嗎?對于一般函數g(x)與h(x)在(-∞,0)上都是增函數,這個我們借助直觀而運用的“定理”對嗎?當g(x)=x且h(x)=x+sinx發現這個“定理”不正確.此題觀察圖象會發現函數g(x)與h(x)圖象一凸一凹,遞增的速度一快一慢,直觀應當正確,如何表述明白呢?建模構造差函數,研究單調性質,利用零點判定定理可以論證的清清楚楚了. 再證明函數g(x)與h(x)圖象在(0,+∞)上有一個交點. 先從幾何直觀出發,借助圖象尋找那個困難的x0>0且g(x0)-h(x0)>0, 由于不知道差函數的單調特征,嚴謹的證明還要構造差函數研究. 變換3.設t=ex,f(x)=ae2x+(a-2)ex-x零點個數問題等價于g(t)=at2+(a-2)t-lnt的零點個數問題,換元法,實現函數結構的變換,成功與否的關鍵是變換后的函數是否簡單、熟悉了. 換元后的函數由二次函數和對數函數組成,研究函數g(t)=at2+(a-2)t-lnt, 當a≤0,g′(t)<0,則g(t)單調遞減; 換元后函數g(t)由二次型函數和對數函數構成,一動一靜凸凹有別,導函數熟悉、親切. 對于此函數同上面函數類型相似的變換,得到一系列解決方法,不贅述. 課本是試題的根本來源,高考試題題在卷面上,根在課本內,高考命題原則是:考查基礎,立足穩定的基礎上創新,那么靠什么保證基礎,靠什么決定穩定,不是試題不變,題型不變,而是課本,課本中不僅有穩定的知識,經典的方法,引申的結論,同時蘊含著重要的數學思想方法.回歸課本,不是拘泥于課本,單一的回顧知識、方法,而是站在整體的高度詮釋系統的知識,讓不同的知識交匯,建構起知識的立體網絡,讓學生思維騁馳在四通八達的立體高速公路上,最終到達數學的巔峰. 教學重視知識、技能、方法的同時,要領悟數學的思想、經歷數學的思維分析、解決數學問題過程,以數學思想為魂,統領復習,這樣才能參透通性通法,而不是陷入同型同法的簡單重復和模仿,解題僵化,縱使刷題無數,遇到新問題,還是遭遇無法解決的囧地.如在函數導數的教學中,加強數形結合、分類討論、函數方程、數學建模、轉化化歸思想和極限思想的運用,加強空間想象能力、抽象概括能力、數學運算能力、推理論證能力和分析問題解決問題能力的提升,加強形象思維、抽象思維(形式思維和辯證思維)、直覺思維和創造思維培養. 鄭毓信教授認為,數學核心素養的基本涵義就在于:我們應當通過教學活動幫助學生學會思維,并能使他們逐步學會想得更清晰、更深入、更全面、更合理. 不可忽視教學活動中,不斷積累、濃縮、升華基本活動經驗,培養既有形象性、可視性又有整體性的數學直觀(幾何直觀、代數直觀),形成直觀—抽象—推理—直觀的螺旋發展模式,真正進入深度學習. 而現實教學,解題中遇到難以突破的關口,諸如套用題型“通性通法”,蒙混過關,借用高等數學公式、定理工具,表面完美解決,實則不解其意,這樣的教學,以分數為目標,到頭來終是難得高分,更可惜的是斷送學生面對思維受阻,山窮水復疑無路,不斷探索,攻堅克難百折不撓后,柳暗花明又一村的寶貴心路體驗,養成追求簡捷與形式優美的思維方式和行為習慣的機會. 著名數學家柯朗在《什么是數學》一書開篇寫道:“數學,作為人類思維的表達形式,反映了人們積極進取的意志、縝密周詳的推理以及對完美境界的追求. 它的基本要素是:邏輯和直觀、分析和構作、一般性和個別性,雖然不同的傳統強調不同的側面,然而正是這些互相對立的力量的相互作用以及它們綜合起來的努力才構成了數學科學的生命、用途和它的崇高價值”,這段激蕩人心的文字啟示我們展示數學基本要素和人們積極進取的意志、縝密周詳的推理以及對完美境界的追求的數學教學,不僅是高效的教學,更是愉悅我們心智的精神饕餮,學會思考的教學才最有價值.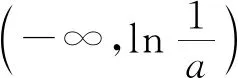
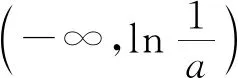
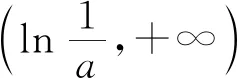
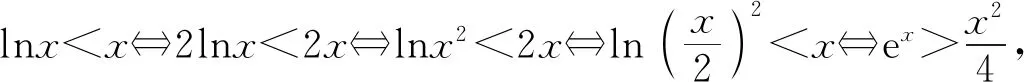
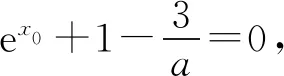
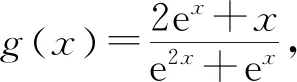
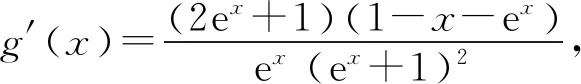
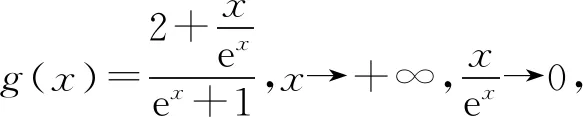
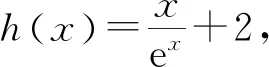
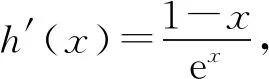
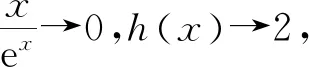
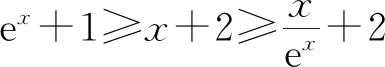
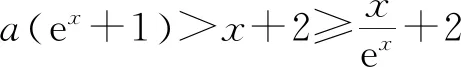
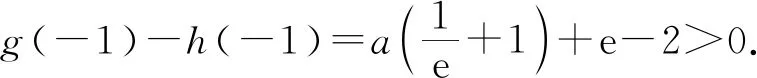

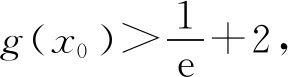
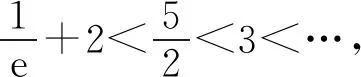
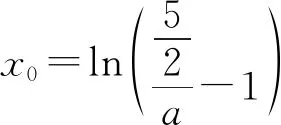
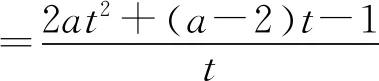
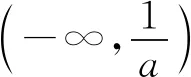
3 教學啟示
3.1 回歸教材,筑牢根基,優化知識結構
3.2 深化思想,提高能力,優化思維品質
3.3 落實素養,積累經驗,構建深度學習
4 結束語

