讓反思與探究成為學生學習常態

倪樹平

(浙江省桐鄉第二中學 314511)

1 引言

《普通高中數學課程標準(2017年版)》明確指出：“普通高中的培養目標是進一步提升學生綜合素質，著力發展核心素養，使學生具有理想信念和社會責任感，具有科學文化素養和終身學習能力，具有自主發展能力和溝通合作能力.數學學科核心素養是數學課程目標的集中體現，是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現，是在數學學習和應用的過程中逐步形成和發展的.教師要把教學活動的重心放在促進學生學會學習上，積極探索有利于促進學生學習方式的多樣化教學方式.教師要加強學習方法指導，幫助學生養成良好的數學學習習慣，敢于質疑、善于思考，理解概念、把握本質，數形結合、明晰算理，厘清知識的來龍去脈，建立知識之間的關聯.”[1]可見，深化普通高中課程改革，踐行《新課標》的核心之一是轉變教師的教育理念，堅持教學方式的變革，特別是學生學習方式的變革，倡導積極主動、敢于質疑、善于思考、自主探究、合作交流的學習方式.筆者認為反思與探究是學生學習方式的重中之重，是促進學生有效學習、發展數學核心素養的必然要求，教師要加強對學生數學解題反思的指導與實踐，激發他們的思維活力，讓反思與探究成為他們的學習常態.下面的教學案例是基于這種理念下的有益嘗試，旨在拋磚引玉，與同行共享.

2 案例呈現

2.1 “向量與不等式恒成立問題”教學案例

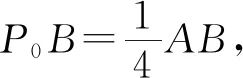
A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

師：解決平面向量問題的一般的通法有哪些？

生1：我們通常可以用代數法和幾何法兩種方法.

師：很好！代數法中的常用方法又是什么？下面請同學們先從代數的角度去探究解題思路.

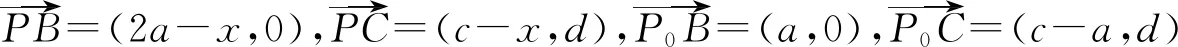
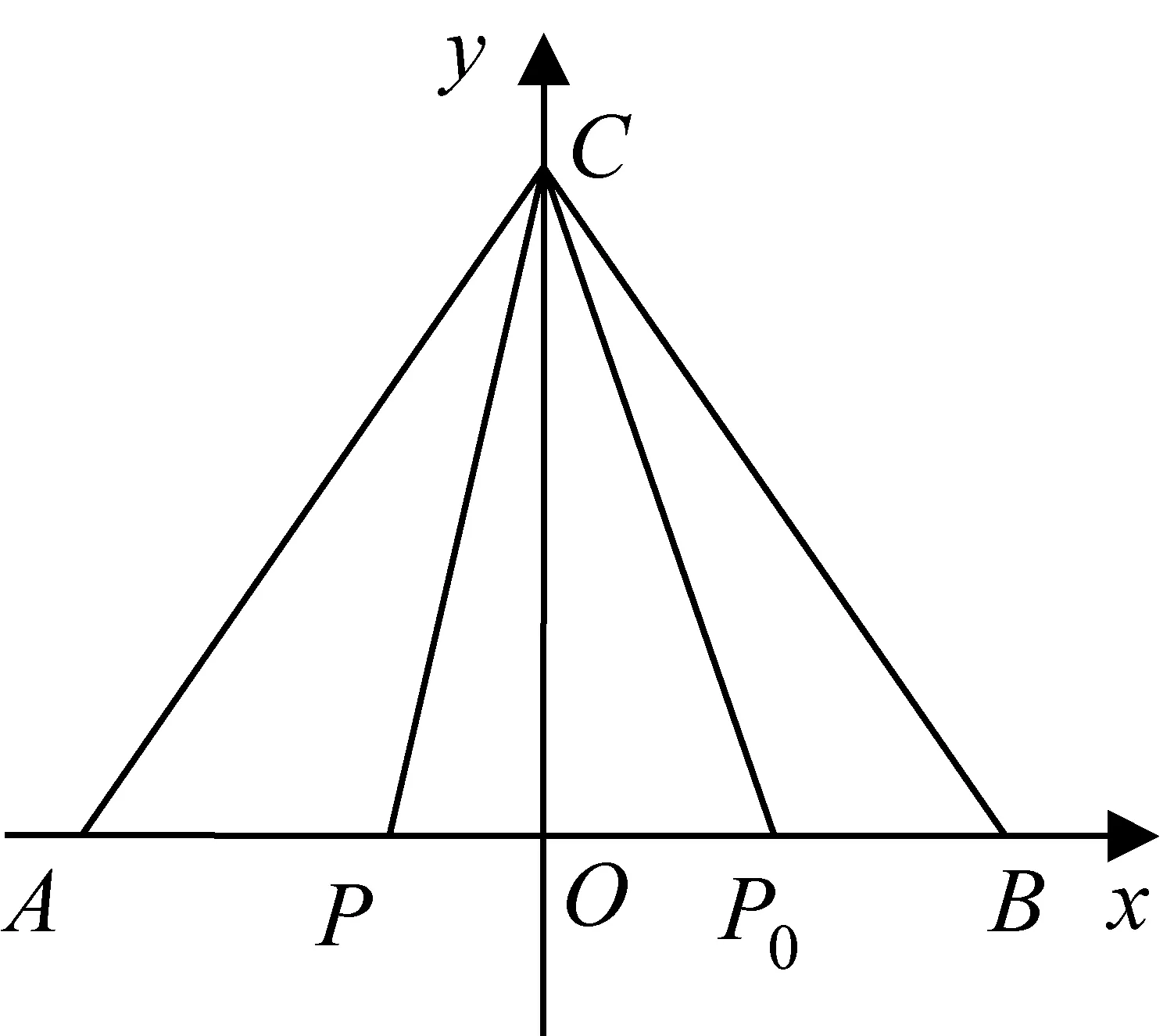
圖1

師：很好！坐標法是代數法中的重要方法，這位同學用坐標法通過向量的坐標運算將不等式轉化為其等價的代數形式，再利用不等式恒成立的思想求解，思路非常清晰！請同學們回顧反思坐標法的本質是什么？

生2：應該是建系設點然后進行代數運算的方法.

師：這就是坐標法，坐標法的本質是將幾何問題代數化，也就是將幾何問題轉化為代數運算.本題是已知向量數量積的不等關系，除了向量數量積的坐標運算還有其他的方法嗎？

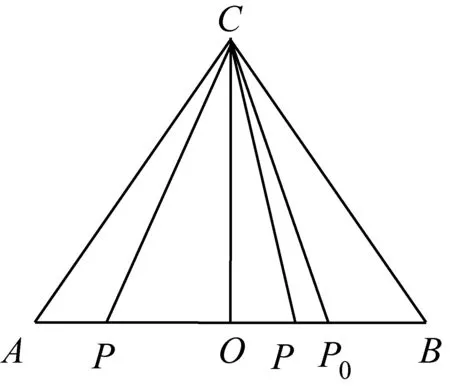
圖2

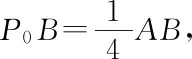
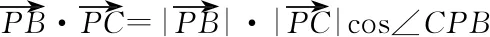
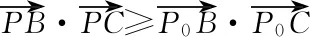
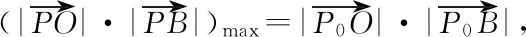
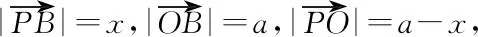
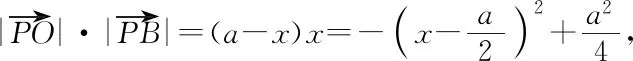
即P在P0時取到最大值，

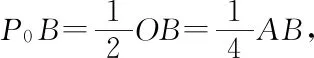
所以AC=BC.

師：很好！向量數量積的定義運算也是代數法，這里用到了向量數量積的幾何意義，體現了數形結合的思想，是一種好方法.平面向量是以平面幾何為背景的一個幾何概念，因此一般來說平面向量問題也可以用幾何法解決，下面請同學們探究怎樣從幾何的角度去思考？

學生沉思，如何將題中的不等式轉化為幾何圖形間的內在聯系對學生的思維挑戰要求更高.

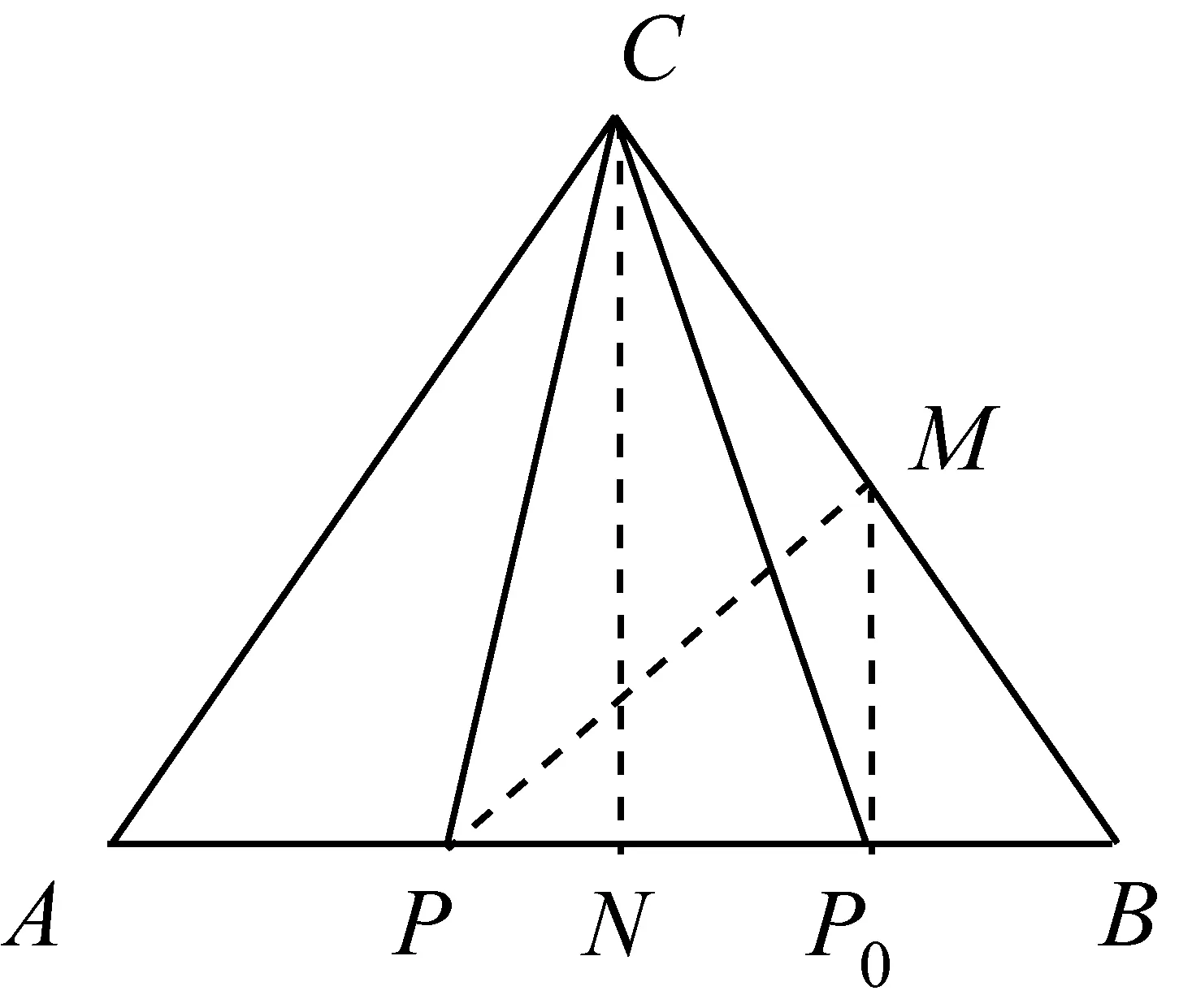
圖3

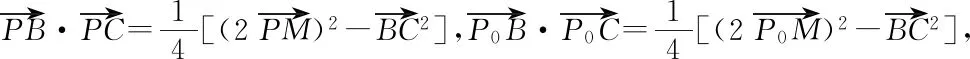
師：很好！幾何法的關鍵是如何將已知條件轉化為幾何圖形間的內在聯系，這位同學利用極化恒等式將向量數量積轉化為向量模的形式，利用向量模的幾何意義和不等式恒成立的思想求解，過程很簡潔！那么，請同學們反思幾何法的本質是什么？

生5：幾何法的本質是尋找數學量的幾何意義求解.

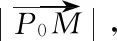
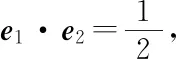
師：請同學們先思考坐標法如何解？

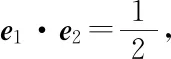
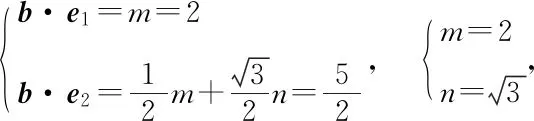
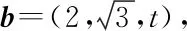
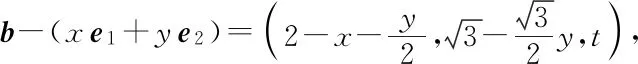
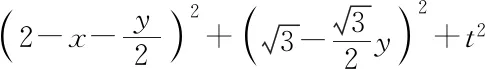
因為對于任意的x,y∈R不等式恒成立，

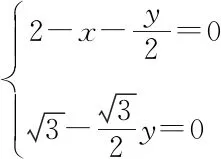
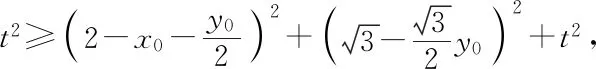
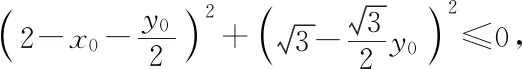
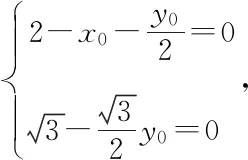
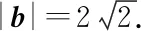
師：很好！本題與前一題目相比是將向量從二維平面向量遷移到三維空間向量，坐標法還是離不開幾何問題代數化的本質，做得非常好！下面同學們還是來探究幾何法，看看幾何法是否更簡潔？

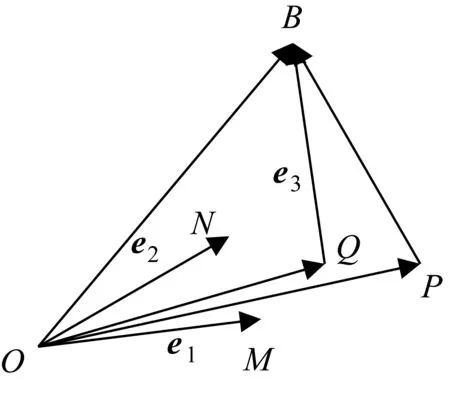
圖4

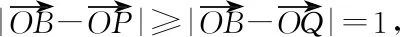
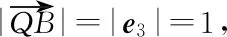
所以e1·e3=e2·e3=0，

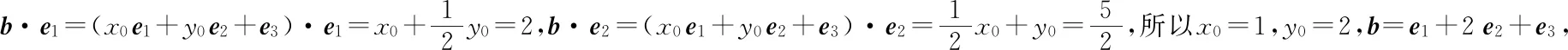
師：非常漂亮！這位同學始終抓住幾何法的本質是找向量的幾何意義，將不等式轉化為兩個向量模的恒不等關系，從題1關于平面中點到直線的距離遷移到空間點到平面的距離，找到了問題的突破口.代數法和幾何法是解決向量問題的兩種基本方法，各有優缺點，代數法入口容易運算量較大，幾何法思維要求較高運算簡潔，同學們要抓住本質，找準入口，學會靈活應用.

2.2 “直線與拋物線位置關系”教學案例

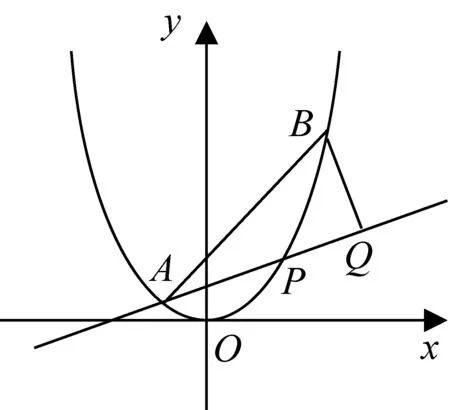
圖5

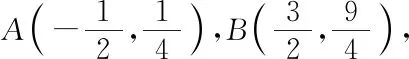
試題評析：本題第一小題考查直線斜率公式，第二小題考查直線方程、兩直線位置關系、弦長公式、直線與拋物線位置關系、求函數最值等知識點，重點考查函數、化歸與轉化、坐標法等數學思想方法.試題入口寬，方法多，可以從不同角度形成不同的解題思路，是培養學生反思解題方向、優化解題方法的一道好題，具有較高的教學運用價值，是我們課堂教學的好素材.

生1：我是根據直線斜率公式來求，

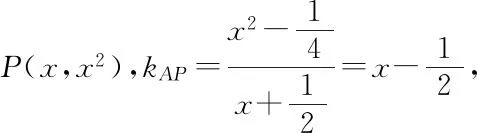
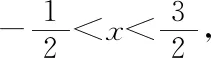
師：很好！這位同學從直線斜率出發將直線AP的斜率表示成關于x的函數，求出范圍，方向準，策略優.請同學們反思從其他角度還有沒有好的方法？

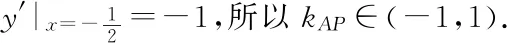
師：這位同學從運動的觀點考慮直線AP的兩個極端位置求出其斜率的范圍，也是本題的一種好思路，策略優，值得點贊.對于第二小題同學們可以從哪幾個方向去思考解題方法？

生3：設直線AP的斜率為k，我想直接寫出直線AP和BQ的方程，解出Q的坐標，再利用弦長公式把|PA|·|PQ|表示成關于k的函數，再由k的范圍求其最大值.

師：我想這種思路非常自然，是一種通法，請同學們按此思路完成解題過程，請生3板演.

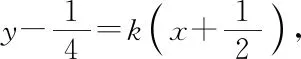
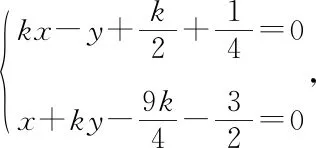
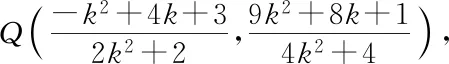
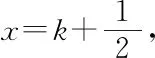
所以|PA|·|PQ|=(k+1)3(1-k)，k∈(-1,1)，

構造函數f(k)=(k+1)3(1-k)，

有f′(k)=3(k+1)2(1-k)-(k+1)3

=-2(2k-1)(k+1)2，

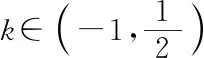
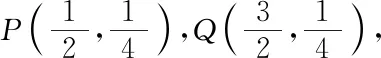
所以|PA|·|PQ|=1;

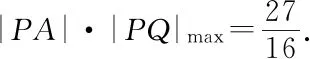
師：請同學們反思解題方向、過程和方法，思考該方法有什么優缺點，更優方法還有嗎？

生4：這種方法比較自然容易想到，但運算過程復雜，不容易做對.

師：生4評價很好！那我們來探究其他的思路，剛才我們把|PA|，|PQ|都看成是弦長的概念，從另一個角度看還是一個什么數學概念？

生5：|PA|，|PQ|也是向量的模長概念.

師：很好！因此，此問題我想從向量的角度來思考方法是否更優？請寫出解題過程.

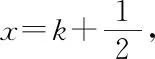
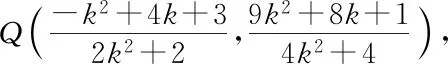
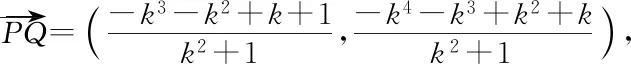
=(k+1)3(k-1)，

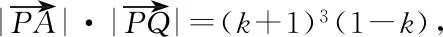
下同上做法.

師：向量的角度思路很好！但這位同學的運算過程還是顯得有點復雜，請同學們反思其運算方向如何？能否選擇更好的運算方向？

生7思維受阻.

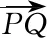
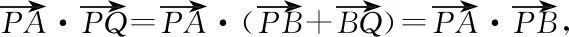
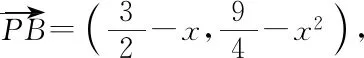
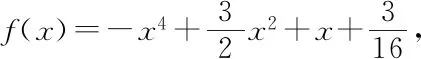
因為f′(1)=0，

f′(x)=-4x3+4+3x-3=-(x-1)(2x+1)2，

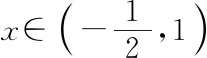
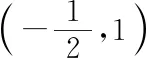
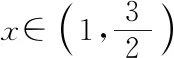
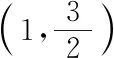
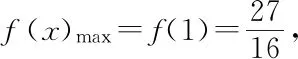
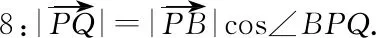
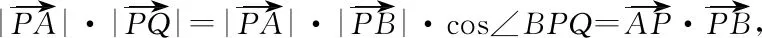
至此，通過反思與探究收獲了三種不同的解題思路，每一次探究都是一次方法優化的過程，學生們積極性都很高，此時教師的追問和引導進一步激發學生的探究欲望，學生陷入了沉思.

師：我想從運動變化的觀點來考慮當P在拋物線弧AB上運動時，點Q的軌跡是什么？

生9：點Q的軌跡是以AB為直徑的半圓.

師：很好！|PA|·|PQ|是圓的一條弦AQ被點P分成的兩條線段長的乘積，我想可否利用平面幾何的知識進行轉化？

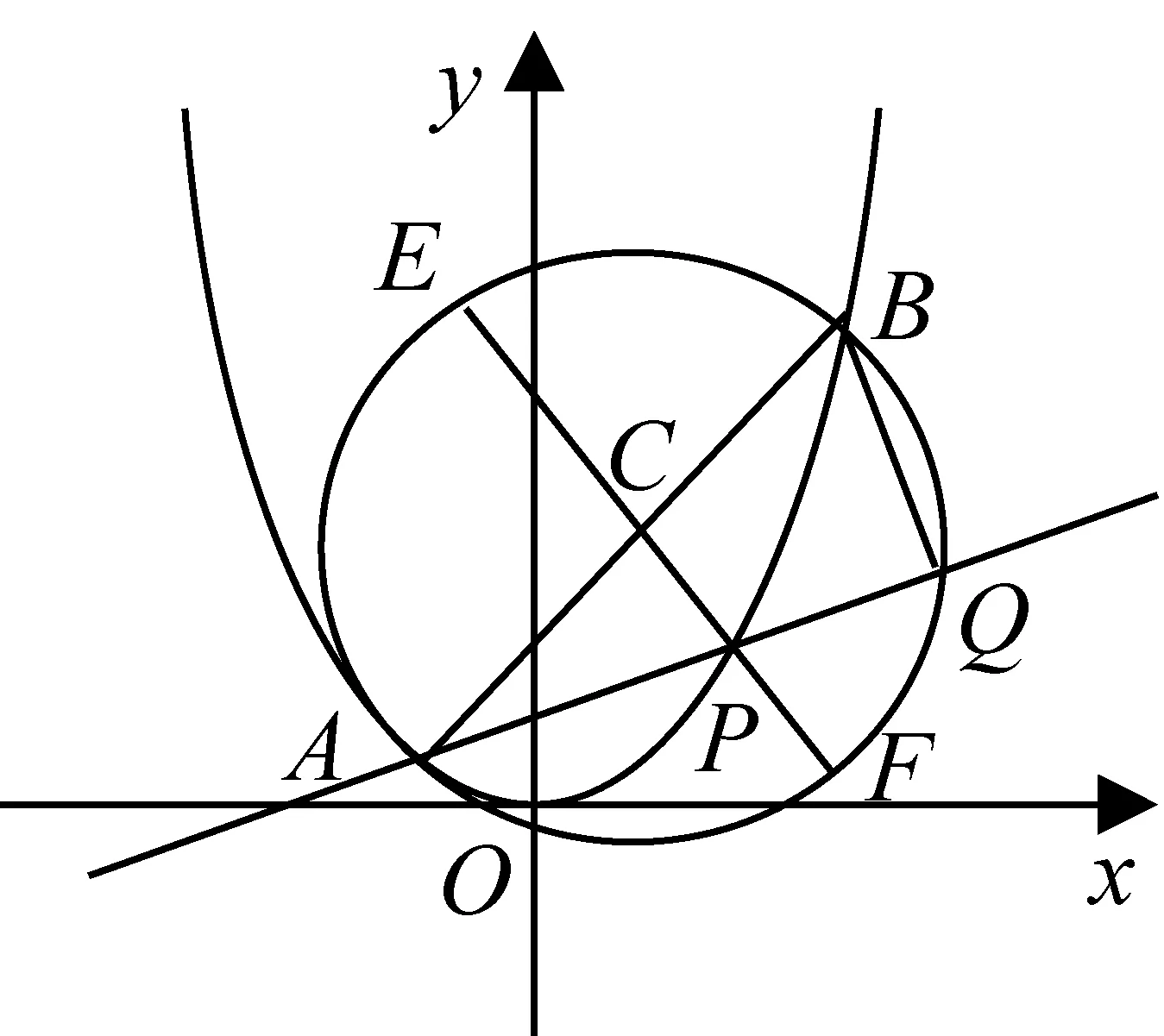
圖6

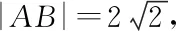
所以|PA|·|PQ|=|PE|·|PF|

=(|CE|+|PC|)(|CF|-|PC|)=2-|PC|2，

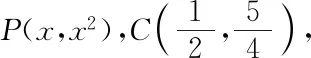
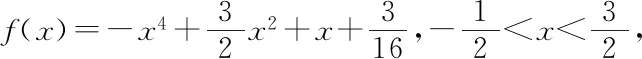
師：很好！該同學回歸到平面幾何的角度求解，思維要求較高，但運算量大大減少，平面解析幾何的本質是用代數的方法解決平面幾何問題，當然平面幾何中的公理、定理在解題中仍舊適用，因此，利用好平面幾何知識解決平面解析幾何問題可優化方法簡化過程.

3 教學思考

3.1 反思學科思想方法，探究知識遷移過程

《普通高中數學課程標準(2017年版)》指出：“高中數學課程要體現社會發展的需求、數學學科的特征和學生的認知規律，發展學生數學學科核心素養，突出數學主線，凸顯數學的內在邏輯和思想方法.”[1]數學思想方法是處理數學問題的指導思想和基本策略，是數學的靈魂和精髓，是形成良好認知結構的紐帶，也是知識轉化為能力的橋梁，是培養學生數學觀念，形成優良思維品質的關鍵.數學解題離不開數學思想方法的引領，每一道數學試題都會考查蘊涵其中的數學思想方法，因此，數學解題教學中讓學生反思學科思想方法，探究知識遷移過程更符合學生的認知規律，提升學生的認知力，有利于發展學生數學學科核心素養.

案例2.1中關于向量的兩個問題，通過代數和幾何兩個視角去解決，教師引導學生反思解決向量問題的兩種通法——代數法和幾何法，在理解兩種方法本質的基礎上探究將向量從二維平面向量遷移到三維空間向量，將平面幾何中點到直線的距離遷移到立體幾何中點到平面的距離，通過對思想方法本質的理解實現了知識的順利遷移過程，建立起知識間的內在聯系，培養函數與方程、數形結合、化歸與轉化等基本數學學科思想方法，發展學生邏輯推理、數學建模、直觀想象和數學運算等方面的學科核心素養.

3.2 反思解題過程方向，探究思路生成過程

問題是數學的心臟，數學教學離不開解決問題，更離不開解題教學，常常聽到有的教師抱怨這個問題我講過N遍了，學生還是不會，問題就出在教師急于完成教學任務，想多講幾個題，總認為讓學生見多識廣，常常忽視了反思解題過程方向，忽視了解題思路的生成過程，導致學生表面上是聽明白了，聽懂了，但實際是知其然，不知其所以然，更沒有厘清其中知識的來龍去脈.學生從聽懂到掌握會做還有很大一段差距，因此，我們把解題教學的內涵定位應該是教學生學會怎樣想、為什么這樣想，教給學生解題的方向，探求思路的生成過程，而不僅是給學生講題、把題講清楚、讓學生聽懂.波利亞解題理論告訴我們：解題要做到“七分構思”即讀題、審題、發散、聯想、歸納，“三分表述”即書寫、運算、訂正、反思與回顧.因此，在解題教學中教師要注重與學生分享自身解題是怎樣構思、怎樣想、為什么這樣想的體會，引導學生反思解題過程方向，注重解題思路與脈絡生成的過程性分析與探究.

案例2.2中在教師的引導下，通過學生的主動反思與探究，生成四種不同的解題思路，在此過程中教師既遵循學生思維的自然形成，又不時融入自己的解題思想，引導學生對問題進行深入的剖析與探究，喚醒學生對知識之間內在聯系的思考，反思概念、信息之間的必然聯系，探求問題轉化的新思路.第二小題中的目標|PA|,|PQ|是弦長的概念，又是向量模長的概念，更是線段長的概念，因此，從弦長、向量數量積和圓冪定理等多個角度探究生成了不同的解題思路，讓學生體會到解題過程是自然的有方向的，又感受到思路的生成過程是水到渠成的，同時在探究思路生成過程中發展數學核心素養.

3.3 反思數學本質內涵，探究方法優化過程

《普通高中數學課程標準(2017年版)》的基本理念指出：“高中數學教學以發展學生數學學科核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質.”[1]數學本質簡單地說就是數學知識內在的根本屬性與規律.高考每年在變，每年都有很多新題，但它對數學本質和數學思想方法的考查卻始終不變.因此，我們在教學中要引導學生反思數學本質、理解數學本質，揭示數學本質，讓學生具有一雙透過現象看本質的“慧眼”，只有引導學生把握數學本質，才能避免“不識廬山真面目，只緣身在此山中”的迷惘，才能充分體會蘊涵其中的數學思想方法，熟練掌握解決問題的通性通法，探究優化解決問題的策略方法，使學生的數學核心素養得到充分的發展.

案例2.1中題1關于向量數量積的不等式轉化問題教師引導學生反思代數法和幾何法本質的基礎上，通過學生自主探究，形成了坐標法、數量積定義運算以及極化恒等式轉化成向量模的幾何意義三種解題思路方法，每一種方法都是在數形結合的基礎上對解題過程的不斷優化.案例2.2中對問題目標|PA|,|PQ|識破它是弦長、向量模長和線段長的概念，將問題回歸到本源去探究思考，更加明確探究方向，指引著整個探究活動高效開展，形成了應用弦長公式、向量數量積坐標運算和應用圓冪定理等不同的解題思路，方法得到優化，過程自然流暢.

4 結束語

波利亞語：“掌握數學就意味著善于解題.”數學學習離不開解題，引導學生在解題過程中進行反思與探究是教師的一種教學理念，主動反思與探究更是學生的一種學習常態.教師在解題教學中要引領學生反思學科思想方法，探究知識遷移過程，反思解題過程方向，探究思路生成過程，反思數學本質內涵，探究方法優化過程，始終讓反思與探究成為學生學習常態，才能讓學生真正領悟學習的真諦，數學的價值，學會數學地思維，把發展數學學科核心素養牢牢根植于數學學習的過程之中.