滾塑烘箱內空氣和模具溫度分布均勻性的仿真研究

劉學軍,江 輝

(1.北京工商大學材料與機械工程學院，北京 100048；2.溫嶺市旭日滾塑科技有限公司，浙江 溫嶺 317511)

0 前言

以往大部分對滾塑工藝加熱階段的理論研究的重點都是放在模具與其中的物料和空氣混合物及熔融塑料之間的換熱機理上，試圖建立一個準確的數值仿真模型來模擬滾塑模具的壁面溫度以及模具內部空氣的溫度[1-4]，從而為滾塑工藝過程的最優(yōu)化控制提供理論依據。在這些研究里一般是將模具的外壁面設置為第三類熱邊界條件，給出烘箱內的溫度以及烘箱內加熱介質與模具的表面?zhèn)鳠嵯禂怠＿@樣處理所得的數值仿真區(qū)域不用包括模具以外的空間，因此也不用考慮滾塑烘箱的具體結構和模具在烘箱內的運動情況，從而簡化了問題。

但上述傳熱模型無法研究某些實際的滾塑工藝問題。例如，在滾塑加熱階段經常會出現模具表面溫度分布均勻性較差的情況，從而使得模具內某些地方的物料過熱，某些地方的物料卻又熔融不徹底，從而破壞了塑料制品的強度和表面品質[5]。由于滾塑烘箱內空氣和模具表面的溫度分布均勻性與烘箱和模具的結構大小、進氣道的形狀以及模具的運動情況等因素都有關系，因此需要建立一個與上述不同的傳熱模型來進行這方面的理論研究。

彭偉等[6]采用FLUENT軟件對滾塑烘箱內的速度場和溫度場進行了數值模擬，并根據計算結果對熱氣流的流入方向提出了改進方案以提高加熱效率。但該文獻在對計算結果的分析過程中更多的是關注模具周圍熱氣流的溫度分布的均勻性，而沒有定量地研究模具表面溫度分布的均勻性。劉學軍[7]79通過數值仿真研究了滑梯形滾塑模具表面溫度分布的均勻性與進風溫度、速度以及進風口和回風口的周向位置間的關系。并采用溫度的標準偏差來定量地表征模具表面溫度分布的均勻性，溫度標準偏差越小表明溫度分布的均勻性越好。但在該文獻的傳熱模型里，進風速度的方向總是與進風口垂直，這與實際情況有一定的差異。另外該文獻也沒有研究模具表面溫度分布的均勻性與模具尺寸間的關系。為了更好地進行滾塑工藝過程的優(yōu)化控制，在烘箱的進氣道里一般還安裝了可轉動的葉片，稱為調整葉片，可以像導流板一樣用來改變進風的方向。關于葉片的轉角對滾塑烘箱內空氣和模具表面的溫度分布均勻性的影響，迄今為止還未見任何文獻有這方面的研究。

本文應用FLUENT軟件通過數值仿真首先研究不同的葉片轉角組合對滾塑烘箱內部空氣的溫度分布均勻性的影響，然后研究不同的葉片轉角組合對滾塑模具的表面溫度分布均勻性的影響，并定量地研究調整葉片轉角對改善上述溫度分布均勻性的有效程度。最后研究在某個特定的葉片轉角組合情形下滾塑模具表面溫度分布的均勻性隨模具長度的變化規(guī)律。這些研究可為滾塑烘箱和模具的結構設計以及工藝參數的優(yōu)化設置提供理論依據。

1 傳熱模型

如圖1所示為滾塑烘箱、模具、葉片、進氣道以及風機的橫截面形狀。該圖還顯示了烘箱進風口和回風口的位置。風機將被加熱的高溫空氣通過進氣道吹入烘箱內部區(qū)域以加熱滾塑模具，通過調整安裝在進氣道里的葉片的轉角可以改變進入烘箱里熱空氣的流動方向和模式。滾塑加熱過程開始后，模具以12 r/min的均勻轉速繞著烘箱的軸線逆時針轉動。已知烘箱的內徑為3.5 m、進風溫度為350 ℃、進風速度為20 m/s并與水平方向成45 °夾角，烘箱內部空氣和模具表面的初始溫度均為27 ℃。

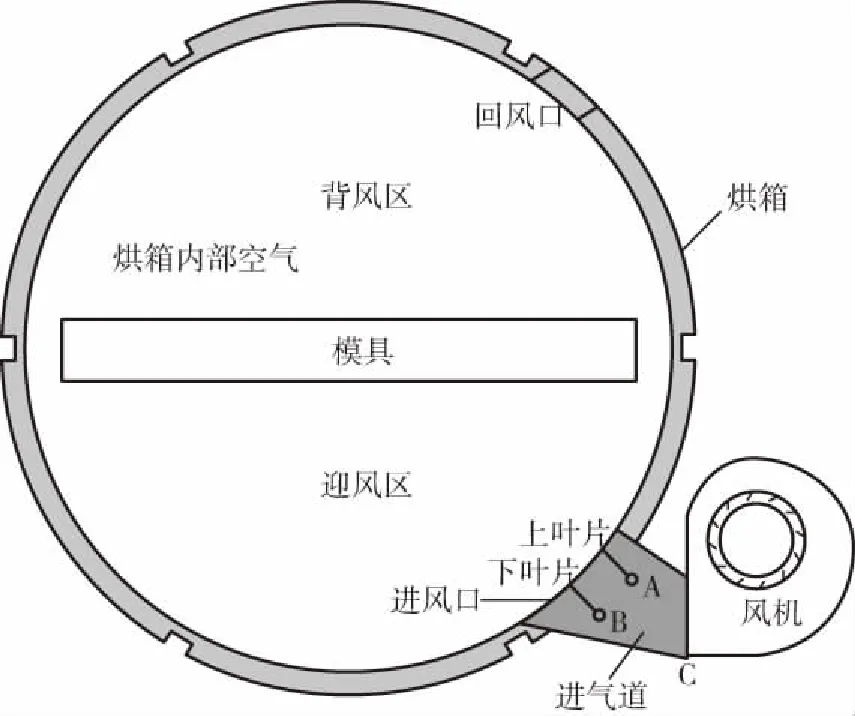
圖1 滾塑烘箱、模具、葉片、進氣道和風機的結構Fig.1 Structure of rotational molding oven, mould, vanes, inlet and fan

計算時長定為5 s，即模具在烘箱內完成繞軸線轉動一周所花費的時間。雖然5 s的計算時長遠遠不能覆蓋整個滾塑工藝的加熱階段，但本文的目的不是為了計算烘箱內空氣和模具表面在滾塑加熱過程中真實的溫度標準偏差，而是為了比較在各個不同的葉片轉角組合情形下烘箱內空氣和模具的溫度標準偏差的相對大小，從而獲得最佳的葉片轉角組合情形。因此只要在所有的葉片轉角組合情形下，用來比較溫度標準偏差的依據是一致的，即都是比較模具完整轉過一周時的溫度標準偏差，那么由仿真結果所得的最佳葉片轉角組合就可以使烘箱內空氣和模具表面的溫度分布最均勻。

上、下葉片的橫截面形狀都是扁長的矩形，其縱向長度均為230 mm、厚度均為10 mm。上葉片轉動中心A與進氣道入口下端點C的水平間距為282 mm，與其豎直間距為408 mm；下葉片轉動中心B與其水平間距為471 mm，與其豎直間距為225 mm。由于結構的限制，這2個葉片的轉角只能在0 °～40 °的范圍內，該轉角是指葉片的縱向與水平方向間的夾角。

為簡化計算，不考慮整個結構軸向尺寸的影響，即這是一個非穩(wěn)態(tài)的二維不可壓縮空氣的流動與傳熱問題。本文將通過FLUENT軟件采用k-ε兩方程湍流模型[8]對其進行數值仿真。另外假設烘箱和進氣道的內壁面以及模具和葉片的外表面都是絕熱的。這個假設與實際情況間肯定是有差異的，但它只會影響表面溫度標準偏差的絕對值大小，而不會影響在各個葉片轉角組合情形下的溫度標準偏差間相對比較的結果，即不會影響本文研究結論的準確性。

本文建立了2種傳熱理論模型—無模具模型和有模具模型。在無模具模型里，圖1所示的模具是不存在的，通過改變上、下葉片的轉角來分別計算在5 s時烘箱內部空氣的溫度標準偏差，從而得到最佳的葉片轉角組合情形。其仿真區(qū)域為烘箱內部空氣以及排除葉片外的進氣道內部空氣。無模具模型的核心思想是假設只要烘箱內部空氣的溫度分布比較均勻，就可以使得放置其中的模具表面的溫度分布也比較均勻。這種模型的優(yōu)點是計算簡單，仿真計算量較小。在有模具模型里，需要考慮模具的形狀大小和轉動情況，通過改變上、下葉片的轉角來分別計算在5 s時模具表面溫度的標準偏差以獲得最佳的葉片轉角組合情形。其仿真區(qū)域為排除模具外的烘箱內部空氣以及排除葉片外的進氣道內部空氣。由于在仿真計算過程中，模具是轉動的，因此該仿真區(qū)域是隨時間變化的。在該模型里，以模具為界把烘箱內部區(qū)域分成迎風區(qū)和背風區(qū)，迎風區(qū)就是正對進風口的模具表面與烘箱內壁面所形成的空氣區(qū)域，而除此之外的烘箱內另一側空氣區(qū)域就是背風區(qū)。

為了衡量通過調整葉片轉角來改善溫度分布均勻性的有效程度有多大，本文定義了一個稱為葉片調整有效率的指標，其計算公式如式(1)所示：

(1)

式中η——葉片調整有效率，%

Smin——在最佳葉片組合情形的溫度標準偏差，即溫度標準偏差的最小值，℃

S0——當葉片不存在時的溫度標準偏差，℃

葉片調整有效率越大，說明調整葉片轉角可以越顯著地改善溫度分布的均勻性。為得到葉片調整有效率，還要采用上述2種傳熱模型分別計算當進氣道里沒有安裝葉片時烘箱內空氣和模具表面在5 s時的溫度標準偏差。關于溫度標準偏差的定義公式詳見文獻[7]81。

2 數值計算結果及分析

2.1 采用無模具模型的仿真結果

圖2分別表示了當上葉片的轉角為0 °、10 °、20 °、30 °、40 °時，烘箱內部空氣溫度的標準偏差隨下葉片轉角的變化規(guī)律。可以看出，當上、下葉片的轉角均為0 °時，溫度標準偏差最小，即當上、下葉片都設置為水平方向時，烘箱內部空氣的溫度分布最均勻。而當上葉片轉角為0 °且下葉片轉角為40 °時，溫度標準偏差最大，即此時烘箱內部空氣的溫度分布最不均勻。

上葉片轉角：1—0 ° 2—10 ° 3—20 °4—30 ° 5—40 ° 6—無葉片情形圖2 烘箱內部空氣溫度的標準偏差隨下葉片轉角的變化曲線Fig.2 Variation of standard deviation of air temperature inside oven with the angle of lower vane

烘箱回風口處的空氣壓力低于烘箱內部的空氣壓力，因此回風口對烘箱內部的熱空氣具有一定的抽吸作用。當上葉片轉角為0 °且下葉片轉角為40 °時,上、下葉片之間形成了一個類似噴嘴一樣的通道，將進氣道內的熱空氣以高速沿斜上方向擠壓進入烘箱內部。這股高速氣流很容易被處于烘箱右上側的回風口抽吸走，這種流動模式會將大部分的熱空氣都導引到烘箱右側的較小區(qū)域里，從而造成在該區(qū)域里空氣溫度較高。而進入烘箱左側的較大區(qū)域里的熱空氣比較少，造成在該區(qū)域里空氣溫度較低。因此整個烘箱內空氣溫度分布的均勻性就很差。當上、下葉片的轉角都為0 °時，就可以利用這2個水平的葉片將進氣道里的熱空氣盡可能多的向烘箱左側區(qū)域導引，從而改善了烘箱內空氣溫度分布的均勻性。圖3(a)和3(b)分別顯示了上述2種情形在5 s時烘箱內部空氣的溫度分布。可以看出，在上、下葉片轉角均為0 °的情形，烘箱左側空氣溫度的最低值比上葉片轉角為0 °且下葉片轉角為40 °的情形要高得多，另外具有最低溫度的空氣分布范圍也比該情形要小。

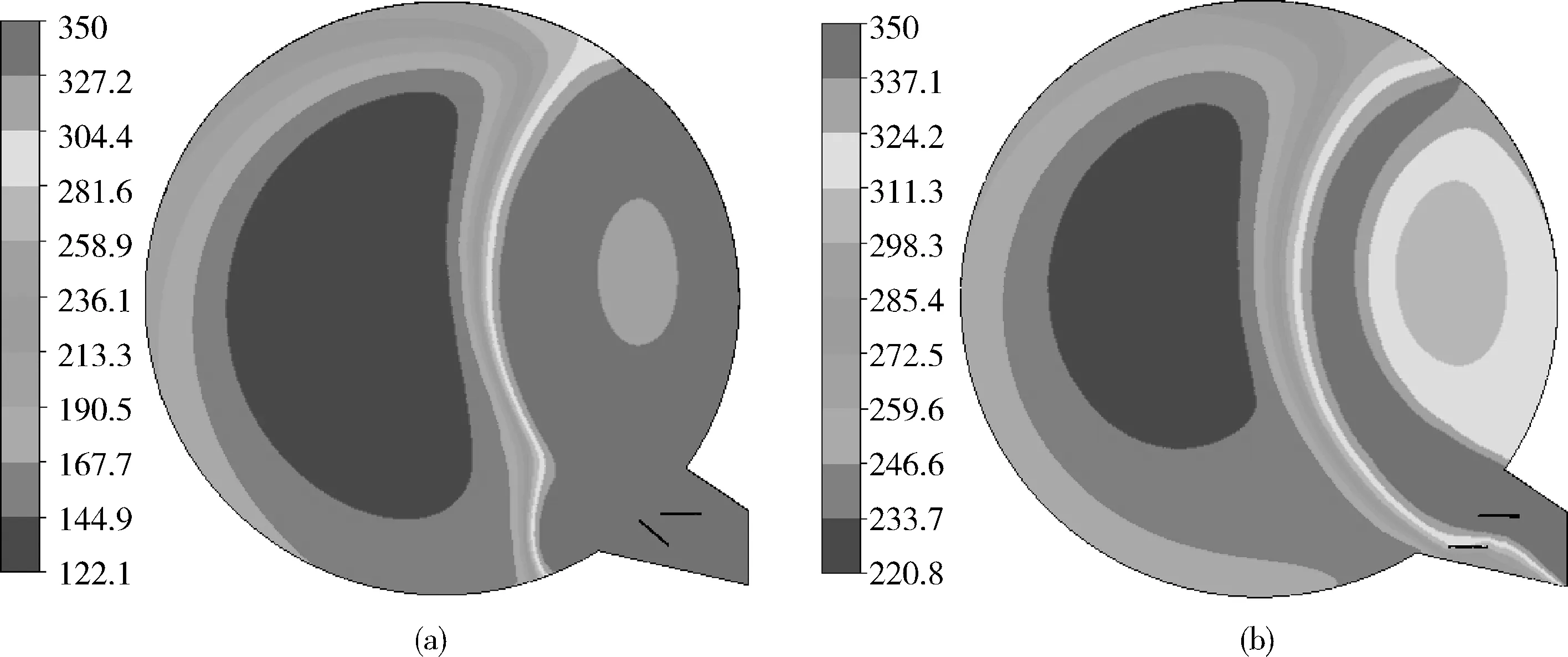
(a) 上葉片轉角為0 °，下葉片轉角為40 ° (b) 上、下葉片轉角均為0 °圖3 5 s時2種情形下烘箱內部空氣的溫度分布Fig.3 Temperature distribution of air inside oven in two cases when time is 5 s

另外值得注意的是隨著上葉片轉角的增大，烘箱內部空氣溫度的標準偏差隨下葉片轉角的變化曲線變得越來越平坦。當上葉片轉角為40 °時，在0 °～40 °的范圍內調整下葉片轉角對改善烘箱內空氣溫度分布的均勻性幾乎沒有效果。這是因為當上葉片轉角為40 °時，無論下葉片調整到該范圍內的哪個角度，下葉片分別與進氣道下壁面和上葉片之間形成的2個通道都不會對即將進入烘箱的熱空氣產生明顯的擠壓作用，因此對烘箱內部空氣的流動狀態(tài)影響較小，故幾乎不會改變其溫度標準偏差的大小。

圖2中的虛線表示當進氣道里沒有安裝調整葉片時，烘箱內部空氣溫度的標準偏差。可以看出在總共25種葉片轉角組合情形中只有7種情形的內部空氣溫度標準偏差大于無葉片時的情形。根據式(1)可以計算出葉片調整有效率為36.5 %，這說明通過調整葉片的轉角可以顯著改善烘箱內部空氣溫度分布的均勻性。另外可以看出無葉片時烘箱內部空氣溫度的標準偏差與上葉片轉角為40 °且下葉片轉角為0 °的情形幾乎相等，這說明在該葉片轉角組合情形，葉片的存在對烘箱內部的空氣流動狀態(tài)幾乎沒有影響。

2.2 采用有模具模型的仿真結果

圖4、圖5分別給出了長度為2 m和3 m的模具，采用有模具模型計算所得的模具表面溫度的標準偏差隨葉片轉角的變化規(guī)律。從圖4可以看出，對于2 m長的模具，在上葉片轉角為0 °且下葉片轉角為20 °的情形，模具表面溫度的標準偏差最小，即此時模具表面的溫度分布最均勻。顯然這與圖2所示的最佳葉片轉角組合情形是不一樣的。這說明使得烘箱內部空氣的溫度分布最均勻一般不能使得模具表面的溫度分布最均勻。雖然采用無模具模型得出的最佳葉片轉角組合情形與采用有模具模型得出的結果有一定的偏差，但從圖4也可以看出，即使按照前者的結果來設置上、下葉片的轉角，所得的模具表面溫度分布的均勻性也好過大部分的葉片轉角組合情形。考慮到無模具模型的仿真計算量比有模具模型的小很多，因此無模具模型的仿真結果也有一定的參考價值，或者說無模具模型的計算方法也有一定的實際應用意義。

上葉片轉角：1—0 ° 2—10 ° 3—20 ° 4—30 °5—40 ° 6—無葉片情形圖4 2 m長模具表面溫度的標準偏差隨下葉片轉角的變化Fig.4 Variation of standard deviation of temperature at 2 m long mould wall with the angle of lower vane

圖4中的虛線表示當進氣道里沒有安裝調整葉片時，2 m長模具表面溫度的標準偏差。可以看出除了上葉片轉角為40 °之外的其他轉角組合情形，其模具表面溫度的標準偏差都比無葉片情形的要小。按公式(1)計算所得的葉片調整有效率為50 %。這說明通過調整葉片的轉角可以大大改善2 m長模具的表面溫度分布的均勻性。另外可以看出無葉片時模具表面溫度的標準偏差與上葉片轉角為40 °且下葉片轉角為0 °時的情形很接近，這說明在該葉片轉角組合情形，葉片的存在對烘箱內部空氣的流動狀態(tài)影響很小，這一點與上述無模具模型的仿真結果是相似的。

從圖5可以看出，對于3 m長的模具，在上葉片轉角為40 °且下葉片轉角為10 °的情形，模具表面溫度的標準偏差最小，即此時模具表面的溫度分布最均勻。這與圖2和圖4所示的最佳葉片轉角組合情形都不一樣。從圖5還可看出，3 m長模具表面溫度的標準偏差隨葉片轉角的變化幅度比圖4所示2 m長模具的要小很多。按公式(1)算出的3 m長模具的葉片調整有效率僅為14.2 %，也遠小于2 m長模具的葉片調整有效率。這是因為較長的模具在轉動時對烘箱內部空氣的攪動作用更加強烈，這使得通過調整葉片轉角所造成的進氣方向的改變對烘箱內空氣流動狀態(tài)的影響不再顯著。因此當模具的長度與烘箱的內徑之比大于0.85時，通過調整葉片的轉角來改善模具表面溫度分布的均勻性就意義不大。

對比圖4和圖5可以看出，如果不采用調整葉片，3 m長模具的表面溫度分布比2 m長模具的更均勻。但采用調整葉片后，在所得的最佳轉角組合情形下，3 m長模具的表面溫度分布就不如2 m長模具的均勻。

上葉片轉角：1—0 ° 2—10 ° 3—20 ° 4—30 °5—40 ° 6—無葉片情形圖5 3 m長模具表面溫度的標準偏差隨下葉片轉角的變化Fig.5 Variation of standard deviation of temperature at 3 m long mould wall with the angle of lower vane

2.3 模具長度對模具表面溫度均勻性的影響

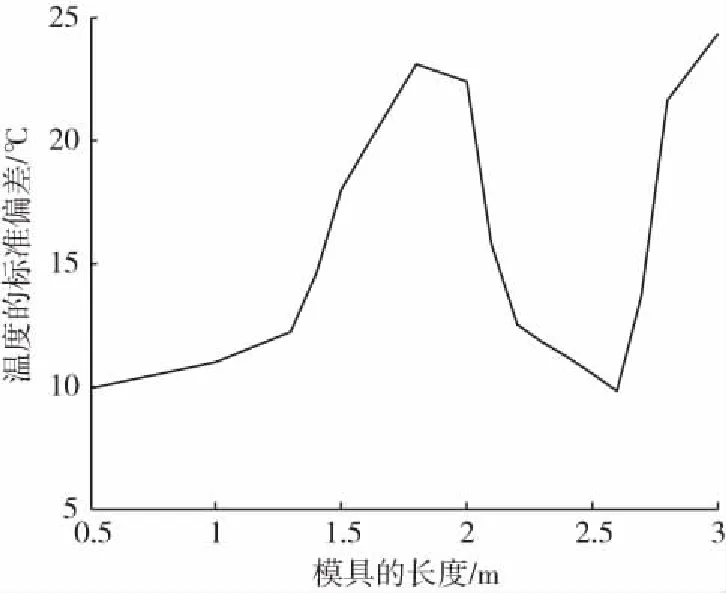
圖6 當上、下葉片轉角均為0 °時，模具表面溫度的標準偏差隨模具長度的變化Fig.6 Variation of standard deviation of temperature at mould wall with length of mould when both angles of upper and lower vanes are 0 °

圖6顯示了在上、下葉片轉角均為0 °的情形模具表面溫度的標準偏差隨模具長度的變化規(guī)律。可以看出，模具表面溫度的標準偏差是隨著模具長度的減小而呈先快速減小然后增大最后再減小的趨勢。當模具的長度小于1.3 m時，模具表面溫度的標準偏差隨其長度的減小而減小的速率變得越來越緩慢，即模具表面的溫度分布慢慢趨于均勻。另外當模具的長度為2.6 m時，其表面溫度分布也很均勻。

長度為3 m的模具雖然對烘箱內部空氣的攪動程度很強烈，但由于模具端部與烘箱內壁面的間距較小，致使迎風區(qū)的熱空氣與背風區(qū)的冷空氣很難彼此混合，因此模具表面溫度分布的均勻性較差。隨著模具的縮短，模具端部與烘箱內壁面的間距開始變大，內部空氣在迎風區(qū)和背風區(qū)之間的流動和相互混合變得比較暢通，從而改善了模具表面溫度分布的均勻性，使得模具表面溫度的標準偏差開始減小。但另一方面隨著模具變短，模具的轉動對內部空氣的擾動程度也會變得越來越弱，而這對改善模具表面溫度分布的均勻性是不利的。當模具的長度減小到一定程度，模具擾動變弱對模具表面溫度均勻性的不利影響要超過空氣在迎風區(qū)和背風區(qū)之間流動混合暢通所帶來的有利影響，從而使得模具表面溫度的標準偏差又開始增大。當模具的長度繼續(xù)減小到一定程度，模具轉動對內部空氣的擾動以及內部空氣在迎風區(qū)和背風區(qū)之間的流動混合對模具表面溫度分布的均勻性都不再有明顯的影響。此時主要是由于模具的表面積越來越小，才使得模具表面溫度的標準偏差又開始變小。

從圖6可以看出，當上、下葉片轉角均為0 °時，在模具長度為1.8 m和3 m處分別有2個溫度標準偏差的高點，即在這2個模具長度，模具表面溫度分布的均勻性最差。當模具長度為1.8 m時，葉片調整有效率比較高，所以還可以通過調整葉片的轉角來有效地改善模具表面溫度分布的均勻性。但是當模具長度為3 m時，如上所述葉片調整有效率比較低，即此時通過調整葉片的轉角來改善模具表面溫度均勻性的效果就不再明顯。因此對于模具長度與烘箱內徑之比大于0.85的情形，更多地需要通過其他的措施來改善模具表面溫度分布的均勻性，如增大烘箱的進風速度[7]82或優(yōu)化設計烘箱的結構。

3 結論

(1)在上、下葉片都設置為水平方向的情形，烘箱內部空氣的溫度分布最均勻；

(2)對于2 m長的模具，上葉片轉角為0 °且下葉片轉角為20 °時，模具表面的溫度分布最均勻；對于3 m長的模具，上葉片轉角為40 °且下葉片轉角為10 °時，模具表面的溫度分布最均勻；

(3)3 m長模具的葉片調整有效率遠小于2 m長模具的葉片調整有效率；在模具長度與烘箱內徑之比大于0.85的情形，通過調整葉片轉角來改善模具表面溫度分布的均勻性的效果不再顯著；

(4)對于內徑為3.5 m的圓筒形烘箱，在上、下葉片都設置為水平方向的情形，當模具的長度為1.8 m和3 m時，其表面溫度分布的均勻性都很差。