捷聯慣導四元數的四階龍格庫塔姿態算法

史 凱,劉馬寶

(1.西安交通大學航天學院,陜西 西安 710049；2.西安機電信息技術研究所，陜西 西安710065)

0 引言

捷聯慣性導航系統不需要任何外來信息,也不會向外輻射任何信息,僅靠慣性導航系統本身就能在全天候條件下進行三維定向[1],通過彈載三軸正交陀螺儀直接解算彈體姿態,其結構簡單,抗干擾能力強。姿態解算是捷聯慣性導航系統的關鍵技術,目前姿態解算的精度一方面受制于陀螺儀自身器件的水平;另一方面是受姿態解算算法的約束,捷聯式慣導姿態更新算法的精度以及復雜程度直接影響整個姿態測量系統的解算精度。

目前姿態解算的主要方法有歐拉角法、四元數法和方向余弦法。歐拉角法不能用于飛行器全姿態解算而難以廣泛應用于工程實踐,且實時計算困難。方向余弦法避免了歐拉角法的“奇點”現象,但方程的計算量大,工作效率低。四元數法只需要求解四個未知量的線性微分方程組,計算量比方向余弦法小,且算法簡單,易于操作,是較實用的工程方法。關于四元數的求解方法,很多文獻都采用數字積分的方法解算載體的姿態[2],或只將龍格庫塔算法應用到彈體的滾轉角解算,并沒有進行三個方向的全姿態角解算[3]。文獻[3]中僅介紹了姿態更新微分方程,應用了龍格庫塔法進行姿態更新,但其算法結構復雜,進行了兩次迭代,運算量較大,實時性和精度不能保證。為了提高姿態解算的精度,根據捷聯慣導姿態更新算法要求高精度、結構復雜度低的需求[4],解決捷聯慣導姿態更新算法能夠滿足實際工程化需求之間的矛盾,提出了捷聯慣導四元數的四階龍格庫塔姿態算法。

1 坐標系定義

首先介紹兩個坐標系:導航坐標系和載體坐標系。

導航坐標系:用Oxnynzn表示,它是慣導系統在求解導航參數時作采用的坐標系,一般選導航坐標系為地理坐標系,原點為載體中心,xn指向東,yn軸指向北,zn軸指向天(當不考慮地球自轉對陀螺輸出的影響)時Oxnynzn即發射坐標系原點即炮位,yn軸指向射向,xn軸與yn在一個水平面指向右,zn軸指向天。

載體坐標系:用Oxbybzb表示,原點為載體重心,xb沿載體橫軸向右,yn軸沿載體縱軸向前,zb軸沿載體立軸向上。載體坐標系與地理坐標系的方位關系可以用姿態矩陣或者姿態角來表示。

兩個坐標系具體關系圖如圖1所示。

本文所有的公式推導及算法均是基于上述坐標系定義的基礎上進行的,按照圖中所示的坐標系各

軸所示,本文繞三軸旋轉的基本坐標系(右手系)轉換矩陣,如下所示[5]:

(1)

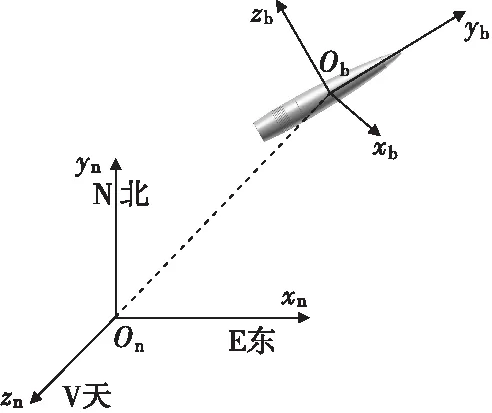
圖1 坐標系示意圖Fig.1 Coordinate diagram

2 四元數的四階龍格庫塔姿態算法

2.1 四元數姿態更新算法

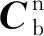
根據第1節三次基本轉換坐標變換陣可以得出由n系至b系的坐標轉換陣如式(2)所示。

(2)

則根據矩陣的性質可以得出:

(3)

根據四元數可確定出b系至n系的坐標變換陣,如式(4)所示。

(4)

綜合式(2)、式(4)可以根據四元數確定的矩陣解算出三個歐拉角如式(5)所示:

(5)

2.2 四階龍格庫塔法姿態解算

四元數描述了剛體的定點轉動,即當只關心b系相對R系的角位置時,可認為b系是由R系經過中間過程的一次性等效旋轉形成的,Q包含了這種等效旋轉的全部信息,uR為旋轉瞬軸和旋轉方向,θ為轉過的角度。根據2.1節可以看出姿態解算的實質是如何更新四元數,四元數微分方程如式(6)所示：

(6)

寫成矩陣形式展開即:

(7)

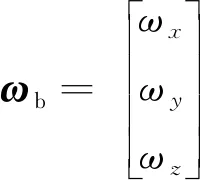
四階龍格庫塔法解四元數微分方程的數值解法思想是在積分區間內進行插值,優化總的斜率得到更新結果,所以其計算精度高于直接積分,龍格庫塔算法階數越高,截斷誤差越小,計算精度越高。在工程上,四階龍格庫塔算法的精度已經能夠滿足大多數精度要求,并且計算復雜度也適宜多數處理器性能。因此,四階龍格庫塔法在工程上被廣泛使用,一般情況下彈道仿真大都采用四階龍格庫塔法。針對式(7)所示的四元數微分方程,相對應的四階龍格庫塔方程公式如下[8]:

(8)

式(8)中，q為四元數向量,h為仿真步長,f為四元數微分方程。經過四階龍格庫塔解四元數微分方程后可以得出下一時刻的四元數數值,由于計算誤差等因素,計算過程中四元數會逐漸失去規范化特性,因此若干次更新后,必須對四元數進行規一化處理，即：

(9)

從計算過程可以看出四階龍格庫塔姿態算法避免了直接積分算法復雜的計算過程、精度差等缺點,其實質是更新四元數微分方程,進而根據更新的四元數求解彈丸的姿態角。該方法只需迭代一次即可更新四元數,算法運算量小,四階龍格庫塔姿態算法相對于直接積分姿態算法中通過級數展開略去高次項從而保證計算精度的方法。其姿態解算的精度可以直接通過仿真步長進行控制,簡單易行,便于調試[9]。

3 算法驗證

3.1 仿真分析

為了驗證算法的正確性和精度,本文在迫彈平臺上對算法進行驗證,從而為后續在迫彈平臺上應用捷聯式慣導系統提供理論依據。仿真模型:120迫彈6 DOF彈道模型,初速200 m/s,初始射角20°,仿真步長0.1 ms,則陀螺四元數解算彈丸姿態與6 DOF彈道模型原始數據外彈道姿態角對比如下圖所示。

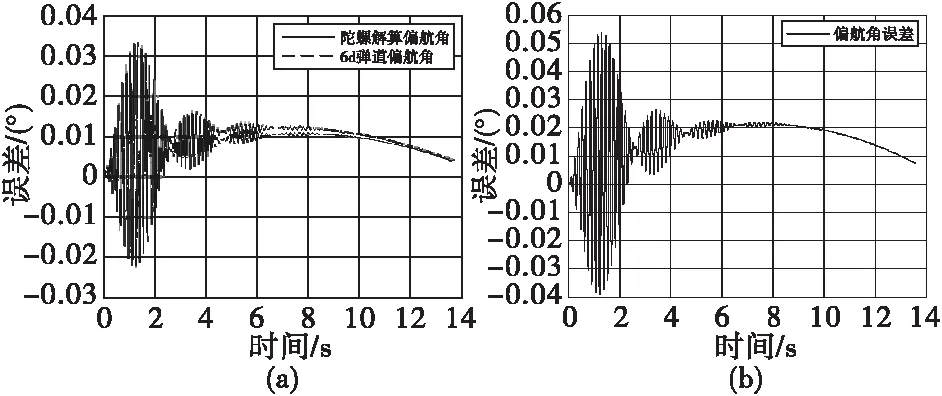
圖2 解算偏航角與理論值對比Fig.2 The calculated yaw angle compared with the theoretical value

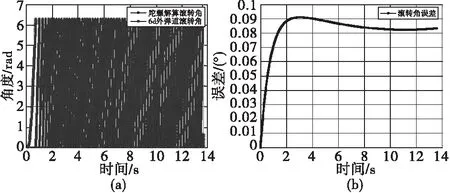
圖3 解算滾轉角與理論值對比Fig.3 The calculated roll angle compared with the theoretical value

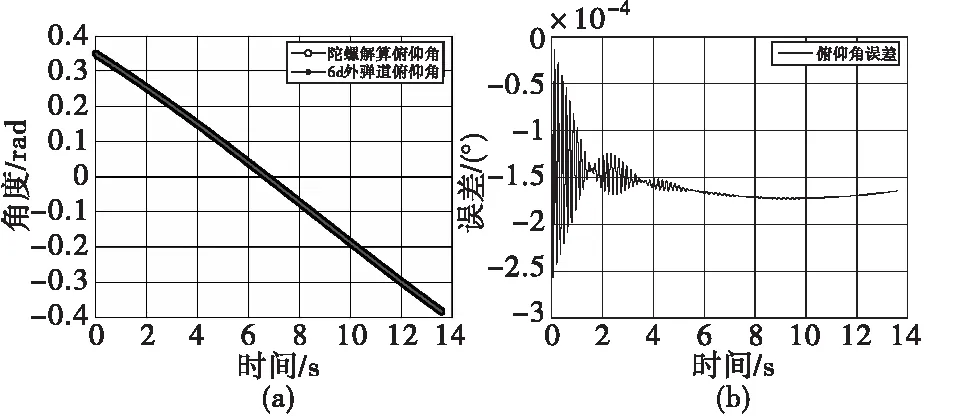
圖4 解算俯仰角與理論值對比Fig.4 The calculated pitch angle compared with the theoretical value

通過仿真結果可以看出,捷聯慣導四元數的四階龍格庫塔姿態算法在迫彈全彈道環境下全向姿態解算精度很高,誤差量級為10-2。由于采樣率對算法的影響也不能忽略,故對不同采樣率對算法精度的影響展開分析,通過改變采樣頻率,對不同采樣率下對滾轉角、偏航角、俯仰角誤差進行了統計如表1，表2所示。

通過表1，表2可以看出120迫彈平臺彈丸轉速在10轉以內采樣率100 Hz已經可以滿足系統要求,同時可以看出隨著采樣率的提高,姿態解算精度也隨之提高。

表1 轉速4 r/s下不同采樣率算法解算誤差

表2 轉速14 r/s下不同采樣率算法解算誤差

3.2 實驗驗證

根據仿真結果設計了相關實驗,開發了彈道飛行姿態測試系統,其結構外形如圖5所示。彈道飛行參數測試裝置實時獲得彈體的三軸角速度,根據三軸角速度信息解算出彈體的姿態,測試裝置如圖所示,其中捷聯慣導三軸陀螺儀的安裝正方向如圖6所示。

圖5 彈道飛行姿態測試裝置Fig.5 Ballistic flight attitude testing device

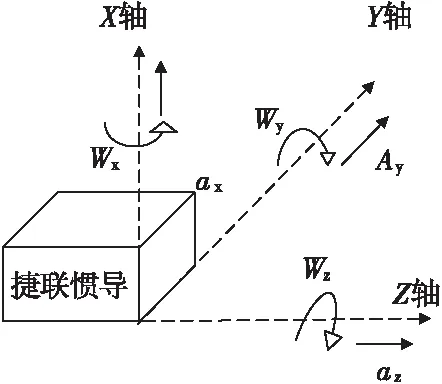
圖6 三軸陀螺儀安裝正方向Fig.6 The three-axis gyro’s positive direction

按照要求設計了彈丸的拋灑試驗,即將彈道飛行參數測試裝置固定于距離地面一定高度的裝置中,點火后將測試裝置彈出,此時通過彈載三軸陀螺儀實時采集到的角速度信息通過彈載記錄儀進行采集試驗后回收測試裝置,讀取彈載存儲器中數據,獲得彈體的三軸角速度,進而通過地面計算機計算軟件解算出彈丸的姿態,完成彈道姿態測試進行彈丸姿態解算同時與高速錄像觀測結果比對,其中實時采集的彈丸三軸角速度和解算得到的彈丸姿態如圖7—圖9所示。

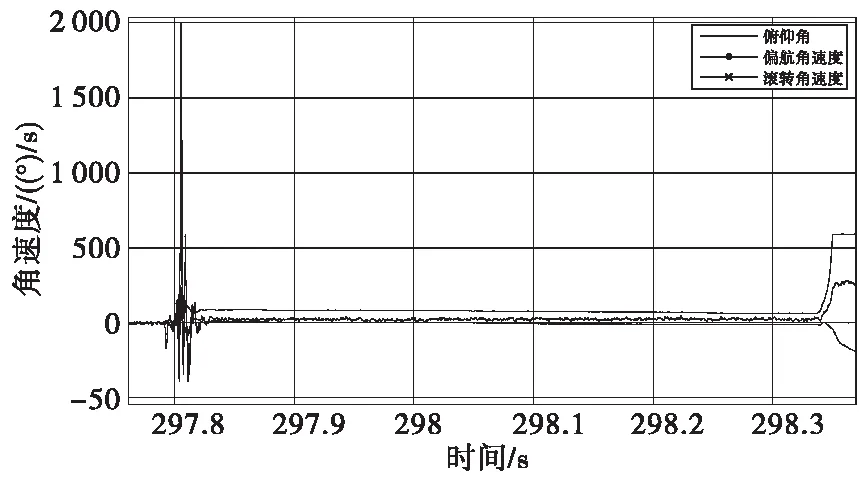
圖7 三軸角速度原始信號Fig.7 Triaxial angular velocity original signal

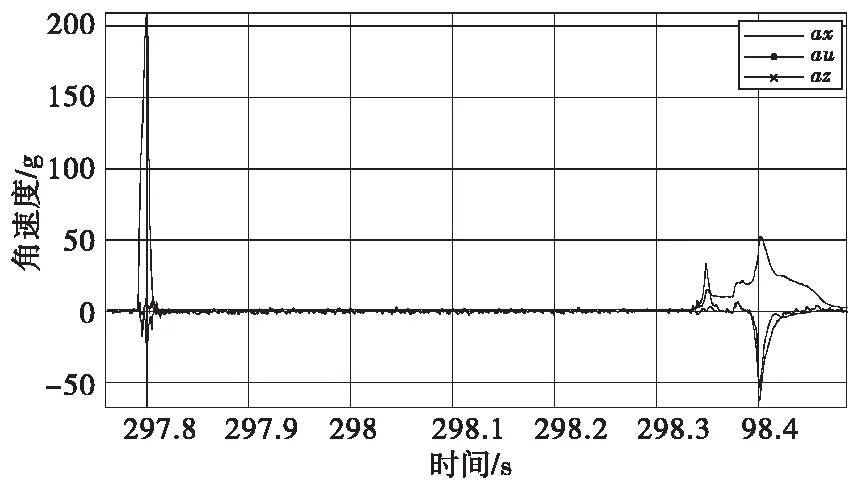
圖8 三軸加速度原始信號Fig.8 Triaxial acceleration original signal

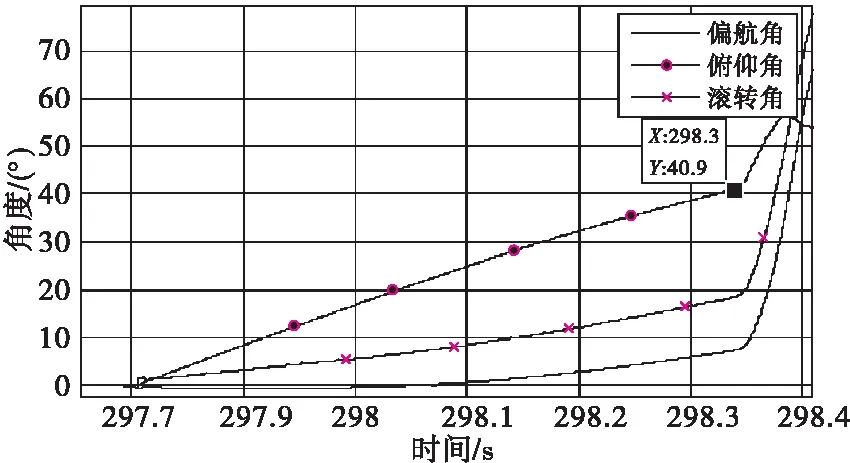
圖9 姿態角解算結果Fig.9 Attitude angle solution results

通過結果可以看出在拋撒過程中姿態變化不大,俯仰角有40°,滾轉角和偏航角基本在20°以內,這與高速錄像觀測的彈丸姿態變化基本吻合,可以真實反映彈丸在拋撒過程中的飛行姿態變化,從而驗證了捷聯慣導四元數的四階龍格庫塔姿態算法具有工程實用性。

4 結論

本文提出了捷聯慣導四元數的四階龍格庫塔姿態算法。該算法僅需一次迭代即可以計算出三個姿態角,通過120迫彈平臺對算法進行了驗證,仿真結果表明該算法結構簡單,精度較高。根據工程實用性和彈上實時性要求,設計開發了彈道飛行姿態測試裝置,同時設計了相關試驗,實驗結果表明算法可以實時計算出彈丸的飛行姿態,可工程化使用,為后續在迫彈平臺上應用低成本捷聯式慣導進行姿態解算奠定了理論基礎。