基于直覺模糊層次分析法的空中目標威脅評估

肖力銘，齊海生，屈濟坤，岳振軍

(陸軍工程大學，江蘇 南京 210007)

0 引言

空中目標的威脅評估是預警探測工作中的重要一環(huán)，現代空戰(zhàn)中，來自不同空域的目標類型種類繁多，除了導彈和作戰(zhàn)飛機外，還會伴隨有假目標和干擾等等。因此，快速準確地對多個空中目標進行威脅程度排序，為我方防空火力分配提供支持，具有十分重要的意義和作用。

當前，目標威脅評估的研究方向廣、研究方法豐富。文獻[1]將云模型和貝葉斯網絡相結合，形成云貝葉斯網絡，建立了基于云貝葉斯網絡的威脅評估模型。文獻[2]運用 D-S理論構建評估體系，生成非同源基本概率指派函數的方案，并利用層次分析和加權平均融合的方法得到最終威脅程度的證據表達，通過賭博概率轉換得到目標的威脅度。文獻[3]提出了基于層次分析法與熵權法的空中目標威脅評估方法，通過結合目標屬性矩陣構建組合賦權模型，從而得到評估結果。文獻[4]通過采用直覺模糊熵算法計算目標屬性權重，并利用多次數據的泊松分布法計算時間序列權重，從而得到基于IFE和動態(tài)VIKOR對空中多目標威脅模型。在研究過程中，不可避免地會出現過分依賴專家評判的情況，因為很多技術指標的確定是理論和實踐相結合的結果。此外，各個評估指標間存在怎樣的關系，如何確定所占權重，同樣是亟待解決的問題。對此，本文提出了基于直覺模糊層次分析法的空中目標威脅評估方法。

1 空中目標威脅評估指標體系構成

空中目標的特征，可以采用多種指標進行描述刻畫，科學合理的評估結果需要從定性指標與定量數據的綜合考量中得出。如表1所述，本文針對空中威脅目標的特點，從目標的狀態(tài)、性能及打擊范圍三個方面入手，涵蓋距離、角度、速度、高度等8個二級指標威脅因子，從不同的側面構建相對完善的空中目標威脅評估指標體系。

表1 空中目標威脅評估評價指標構成

2 基于直覺模糊層次分析法的威脅評估

直覺模糊集的概念是保加利亞學者Atanassov在1983年提出的，是對Zadeh所提的傳統模糊集理論的拓展。因為直覺模糊集同時考慮了隸屬度、非隸屬度和猶豫度這三方面的信息，因此在處理模糊性和不確定性等方面比傳統模糊集更加具有靈活性和實用性[6]。30多年來，有關直覺模糊集理論的研究受到了國內外學者的密切關注，并且在邏輯規(guī)劃、市場預測、機器學習和決策等領域都得到了廣泛的應用[7-8]。

2.1 建立直覺模糊判斷矩陣

為了更加全面直觀地刻畫偏好信息，需要建立直覺模糊判斷矩陣：

Z=(zij)n×n

(1)

式(1)中，zij=(μij,νij)，i,j=1,2,…,n，表示決策者對兩個指標重要性進行比較后的評價結果。該結果用直覺模糊數來表示，對應關系如表2[9]所示。

令μii=0.5，同時，存在zij=(μij,νij)和zij=(μji,νji)，滿足μij+μji=1。

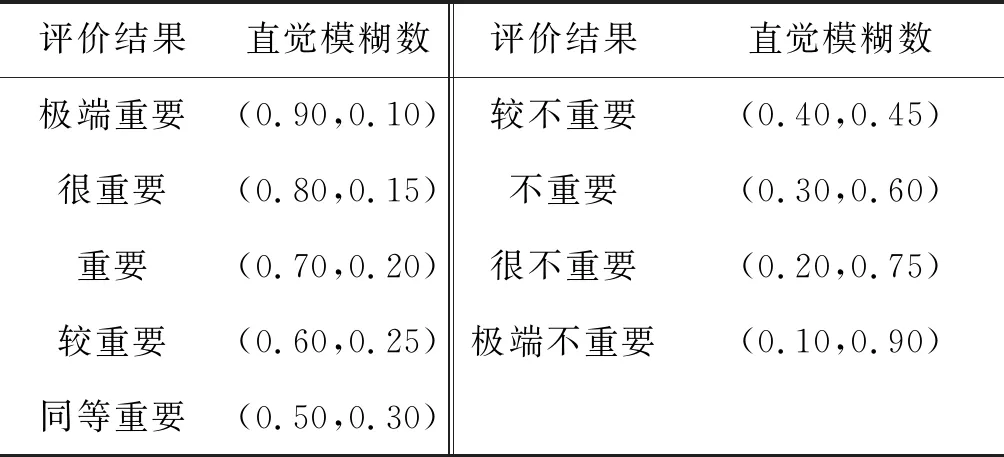
表2 評價結果與直覺模糊數對應關系

2.2 進行一致性檢測及修正

在在直覺模糊層次分析法中，為了避免出現不可信結果甚至錯誤，需要對直覺判斷矩陣的一致性進行檢驗。文獻[10]提出構建積型一致性直覺判斷矩陣：

(2)

從而建立一致性檢驗指標。

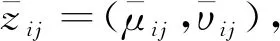
(3)

(4)

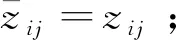
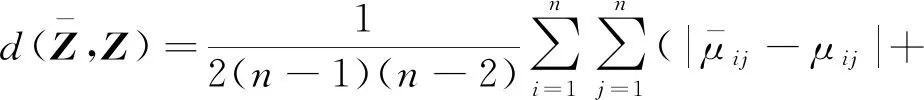
(5)

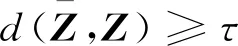
2.3 權重的確定

矩對于通過一致性檢驗的直覺判斷矩陣，由式(6)[10]可以得到同一層次中各指標間的權重關系w=[w1,w2,…,wn]，其中，

(6)

由表1可知，評價指標中兩級指標分別為3個和8個，一級指標與二級指標間各自的指標權重向量均為直覺模糊數，令兩級權重向量分別為wo和wt。本文引入復合的直覺模糊數算子：

(7)

來計算同一指標層各因素相對于目標層的組合權重，其中i=1,2,…,n2。關于直覺模糊運算算子參見文獻[6]。

2.4 指標標準化

在指標類型中包含效益型和成本型兩個經典屬性類型。其中，效益型指標又叫正向指標，即指標值越大目標威脅程度越高，成本型指標又叫反向指標，即指標值越小目標威脅程度越高。可將前文指標體系中的各個指標按屬性類型分為正向型和反向型，其中正向型指標有目標的速度、探測半徑、機載武器能力和作戰(zhàn)半徑，反向型指標則包含了空中機動目標的距離、高度、角度和隱身性，指標的標準化方法如下。

對于正向型指標和反向型指標的標準化值可以分別通過式(8)和式(9)來計算：

(8)

(9)

2.5 綜合評估

利用指標標準化中的方法，將m個待評估目標歸一化，得到指標值Y=(Yij)m×n，結合各指標相對于目標層的組合權重W，可以得到綜合評價值：

(10)

式(10)中，i=1,2,…,m。值得注意的是，此時的值F=(μF,υF,πF)仍是直覺模糊數，為了對其進行排序比較，可以通過得分函數來完成。本文定義機動目標威脅評估的得分函數為：

(11)

由上式可將直覺模糊數F轉化為可以進行比較的φ(F)，φ(F)的值越大，該目標的威脅程度就越高。

3 仿真實例

某日，我防空識別區(qū)闖入4架不明國籍戰(zhàn)機，經我方區(qū)域預警探測系統跟蹤識別得知，4架飛機中有兩架為同型殲擊機a1、a2，兩架為同型轟炸機b1、b2。戰(zhàn)機基本情況如表3所示。

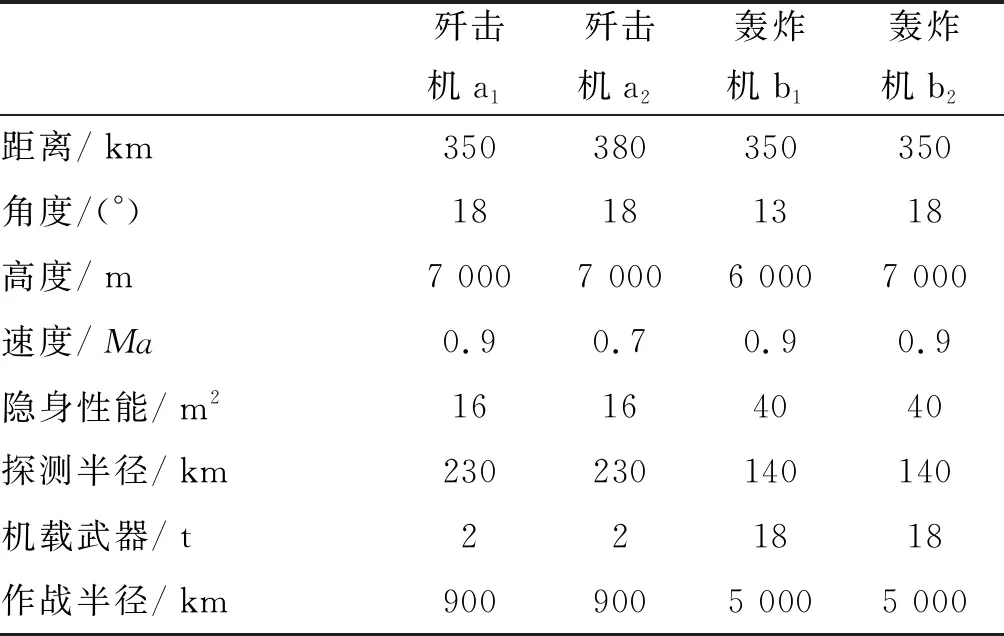
表3 目標基本情況

根據權威評估，可以得到評估指標體系準則層和指標層中各指標間兩兩進行比較得到的定性評語。由表2，將結果轉化為直覺模糊數，可以分別得到準則層和指標層的直覺判斷矩陣Zzz和Zzb：

Zzb=

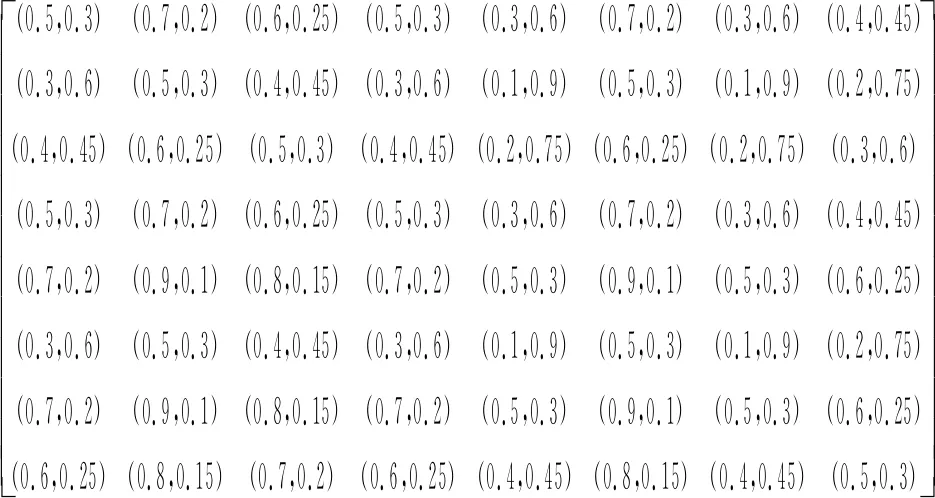
計算同一指標層各因素相對于目標層的組合權重，得到：

W=

[(0.078 1,0.811 2)(0.061 2,0.849 8)(0.069 7,0.829 4)(0.078 1,0.811 2)

(0.094 8,0.785 3)(0.061 2,0.849 8)(0.094 8,0.785 3)(0.086 5,0.797 2)]

根據2.4節(jié)將四架戰(zhàn)機基本情況中的參數分別進行歸一化，進而得到各戰(zhàn)機的指標值矩陣：

Y=

利用指標值矩陣，結合各指標相對于目標層的組合權重W，根據式(10)可以得到綜合評價值：F=[(0.217 6,0.541 1) (0.194 9,0.580 4)(0.304 0,0.407 6) (0.284 3,0.438 0)]根據機動目標的威脅評估得分函數公式(11)，可以得到各個目標的威脅程度值：

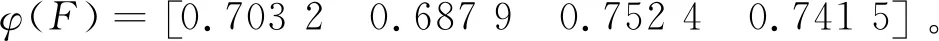
由此可以得出4架戰(zhàn)機的威脅程度排序：b1>b2>a1>a2，符合直觀判斷。而采用傳統模糊分析方法所得到的結果為b2>b1>a1>a2，當空中目標數量更加龐大時，評估結果則會對作戰(zhàn)決策帶來重大影響，顯然本文所述方法更加科學合理。

4 結論

本文提出了基于直覺模糊層次分析法的威脅評估方法，有效避免評估主觀性強的問題，通過構建反映空中目標威脅的兩級評估指標體系，運用直覺模糊集理論更加科學地刻畫指標間的相互關系，結合層次分析法有機結合定性指標與定量數據，由得分函數求得目標的威脅程度并排序，為后續(xù)的火力分配及作戰(zhàn)決策提供有力依據。通過案例分析，驗證了方法的可行性，實現了綜合評估的靈活性和實用性。