巧用類比思想 提升核心素養

陳龍珠

（尤溪第一中學，福建 尤溪 365100）

類比思想是一種重要的數學思想，是高中數學課堂中所提出的先進思想理念。所謂類比就是“為了促進對未知事物的理解，通過與已知事物的比較，進而發現兩者之間在特征和形式上的類似之處，并建立兩者之間的關聯，運用推理的方法解決問題”。而類比思想就是在類比的基礎上形成的基本邏輯思維，通過對相似的事物進行比較分析，從中總結出規律。因此，在數學教學中，通過類比可以利用已知解決未知，利用簡單解決復雜的問題，培養學生解題能力、思維能力，提升數學學科核心素養。

一、巧用類比，學習新知識

高中數學相對于初中數學而言，知識點更多、難度更大，很多學生對一些概念、定理、公式一知半解，不甚理解其中含義，往往死記硬背，一定程度上制約了學生靈活運用相關知識的能力。如何合理引導學生理解要義，類比方法就是一種最便捷最有效的辦法。《普通高中數學課程標準（2017年版）》指出：“類比是發現和提出數學命題的重要途徑。”類比就是一種相似，把兩個數學對象進行比較，找出它們相似的地方，從而推出這兩個數學對象的其它一些屬性也有類似的地方。眾所周知，高中數學常有并列的兩個數學對象，二者有諸多相似點，教師就要善于運用類比的方法引導學生從已知推理未知。

例如，在教學等差數列與等比數列時，可采用類比方法進行對照式教學。

定義教學時，等差數列的定義是一個數列從第2項起后一項與前一項的差為同一個常數，即anan-1=d。類比可得，等比數列是一個數列從第2項起后一項與前一項的商為同一個常數，即=q；

通項公式an推導時，通過累加法求得等差數列的通項公式an=a1+(n-1)d，類比累加法，可通過累乘法求得等比數列的通項公式an=a1·qn-1；

推導前n項和公式sn時，等差數列的前前n項和采用倒序相加法求得，即sn=na1+d，類比倒序相加法，可用錯位相減法得到等比數列的前n項和公式，即sn=

在推導性質時，由定義得：若m+n=p+q,則am+an=ap+aq，類比可得等比數列的相應性質：若m+n=p+q,則aman=apaq。

采用類比教學，鏈接新舊知識，既可鞏固舊知識達到溫故而知新的效果，又能有效引導學生開展對未知領域的探索，有利于培養學生的邏輯思維能力。在數學教學過程中，我們常常會有“似曾相識”的感覺，如果教學能夠抓住知識間的相似之處，再合理進行類比教學，可獲得意想不到的教學效果。

二、巧用類比，構建知識網

高中數學教學，知識點間存在著一定的邏輯關聯，教師要利用其中的相似點，引導學生進行勾連，以點代面，由孤立到系統，總結發現一類問題的解決辦法，不斷豐富已有的知識體系，構建相應的數學知識體系，形成知識網絡，拓展思維，融會貫通。

例如，在學習立體幾何線線平行與面面平行時，相關的定義、判定、性質及結論可采用類比教學。

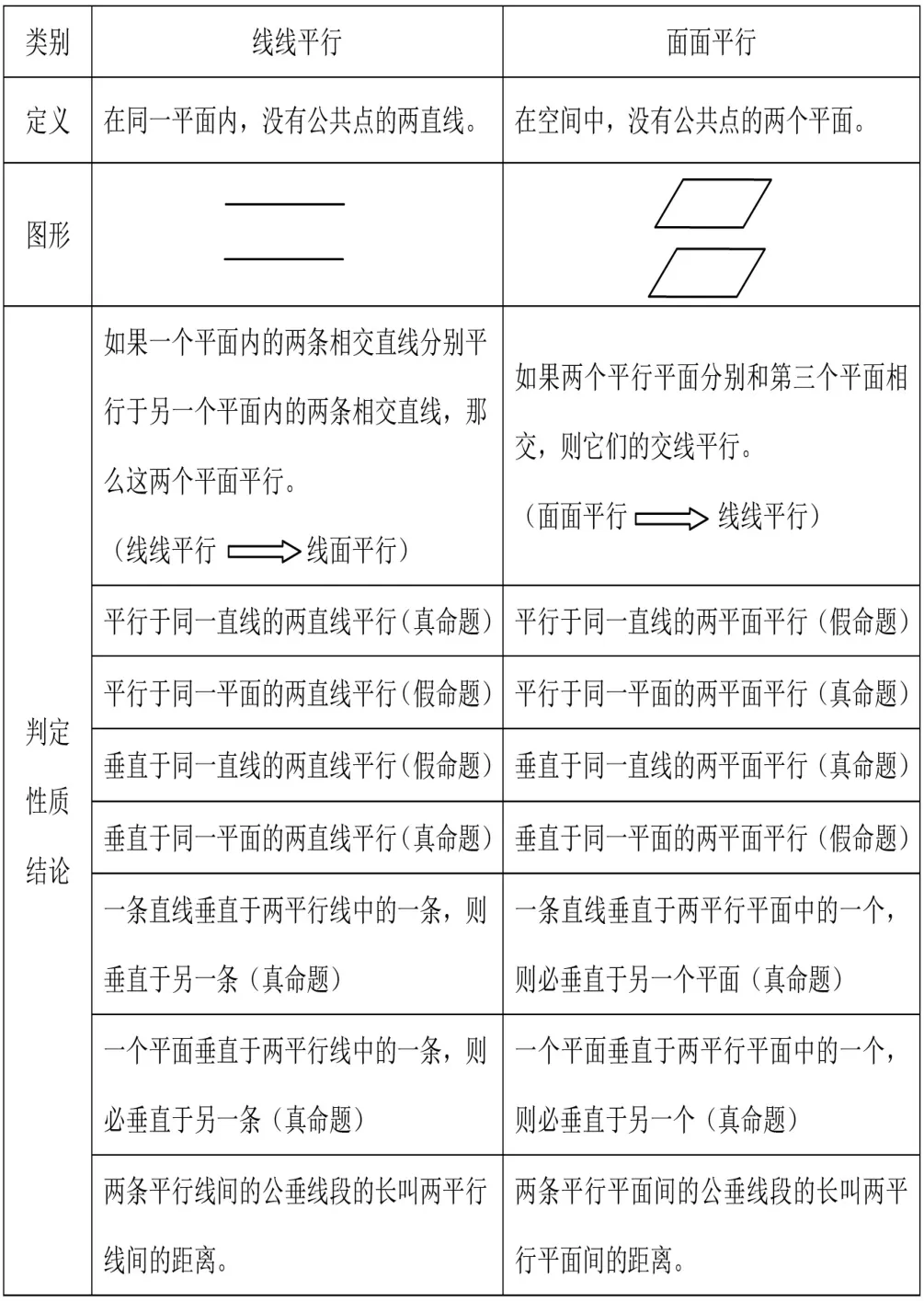
因此，教師利用類比方法，可將學科知識內容的不同板塊建立良好的關聯，幫助學生厘清學科知識內容不同板塊的聯系，在學生的腦海里，不再是獨立的知識點，而是一張知識網，從而逐漸構建學生自身的學科知識體系。

三、巧用類比，拓展新思路

美國著名的數學家波利亞在他的世界名著《怎樣解題》中說過：“在求證或求解一個問題時，如果能發現一個類比題，那么這個類比問題可以引導我們達到原問題的解答。”可見，要打開解題思路就得對可能的解題方法進行猜測，尋找類比問題。當學生遇到新的問題時，教師要鼓勵學生加強審題訓練，對已知條件多讀幾遍，聯系自己熟悉的條件，對做過的題目和題型進行歸納總結，找找其中的規律，往往可以得到正確的解題思路。

例如，在等差數列{}an中，若a10=0，則a1+a2+…an=a1+a2… +a19-n(n＜19,n∈N)成立，類比上述性質，在等比數列中，若{}bn，則有等式成立。

學生解決此類問題時，學生能否借助學科不同板塊之間的關聯性進行有效地類比，是解決此類問題的關鍵，類比等差數列與等比數列的性質便可以得到結論：

等差數列性質：若m,n,p,q∈N*且m+n=p+q,則am+an=ap+aq

等比數列性質：若m,n,p,q∈N*,且m+n=p+q,則 am·an=ap·aq

故猜測本題的答案為：

b1b2…bn=b1b…b17-n(n＜17,n∈N*)

事實上，對等差數列{}an，如果 a10，則有:an+1+a19-n=an+2+a18-n=…=0

因此：

a1+a2+…an=a1+a2+…an+(an+1+an+2+…+a19-n).

而對于等比數列{}bn，如果 b9=1，類比性質可得：an+1a17-n=an+2a16-n=…=1

從而，可推導

b1b2…bn=b1b2…b17-n(n ＜ 17,n ∈ N*)成立。

再如，已知x,y,z均為正整數，

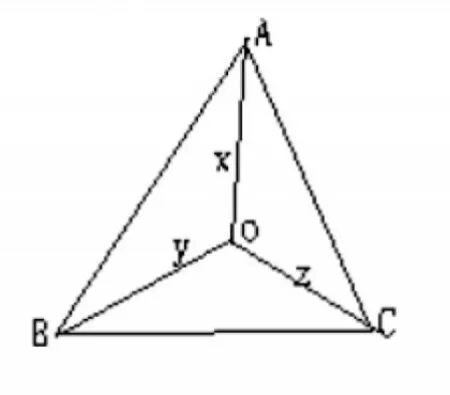
如圖所示：作 △ABC,∠AOB=∠AOC=∠BOC=120°

設OA=x,OB=y,OC=z

由余弦定理得：

又因為AB+AC＞BC，所以原不等式得證。

可見，在解題時，遇到一些問題，注重已有的認知進行類比教學，常有“柳岸花明又一村”的感覺，從而實現知識的正遷移，使問題得以解決。

總之，在高中數學教學過程中，教師要適時創設問題情境，引導學生靈活運用類比方法，鏈接新舊知識，構建知識網絡，拓展解題思路，真正提高數學教學的效率，促進學生邏輯思維的發展，提升數學學科核心素養。