基于核心素養背景下初中幾何最值問題的解題方法

蔣 雁

(廣東省韶關市廣東北江實驗學校 512000)

一、運用轉化思想―將問題轉化成基本的最短路徑模型

在運用轉化思想構建最值問題時，一般會用到平移變換、抽對稱變換以及旋轉變換.平移變換更多的是通過平移線段來構造平行四邊形，借助對邊平行且相等來找到相對應的最短線段，從而解決問題求得最值.軸對稱變換更多的是利用垂線段最短來解決問題，一般我們可以借助全等三角形、勾股定理以及相似三角形等來確定最值從而求出最小值.接下來我對旋轉變換作進一步分析：

例如：已知P是銳角三角形ABC內的一個點，且使PA+PB+PC最小，試確定點P的位置，并證明你的結論.

由于題干只有文字信息，而對于幾何圖形必須通過圖形信息去挖掘題目信息，因此，我們先根據題干信息作出如下解析圖:

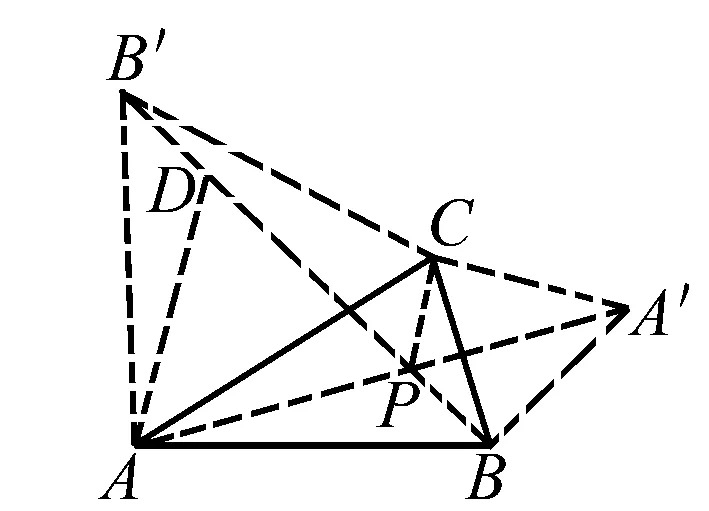
首先畫出三角形ABC，接著以AC為三角形的一邊向外作等邊三角形ACB′，再以BC為三角形的一邊向外作等邊三角形BCA′.連接BB′以及AA′，此時BB′和AA′相交于一點P，而這一點P就是我們所要求的.

接下來證明PA+PB+PC=PD+PB+DB′是一個定值.由于△ACB′和△BCA′是等邊三角形，因此得出結論：CA′=CB，AC=B′C，∠ACA′=∠BCB′，因此△ACA′全等于△B′CB.又因為∠B′BC=∠AA′C，所以得到∠BPA′=∠BCA′=60°，所以∠APB′=∠BPA′=60°.此時，在PB′上截取PD=AP，將AD、CP連接.由PD=AP，∠APB′=60°，得出△APD為等邊三角形.又由AP=AD，AC=AB′，∠DAB′=∠PAC，得到△PAC全等于△DAB′，于是得到結論線段CP=B′D.從而知道PA+PB+PC=PD+PB+DB′是一個定值 .

然后需要證明PA+PB+PC為最小值，在△ABC的內部任意取一點M，如右圖所示，此點M和點P不相同，將MA、MB以及MC連接起來，此時構成了△AMC，將△AMC以圖中的A點為中心，逆時針旋轉60°，得到一個新的三角形AGB′.在旋轉的過程中，我們不難得到AC=AB′，AM=AG，MC=GB′，此時可以得出△AGM是一個等邊三角形，由此推出MA=MG.由此，我們可以得到MA+MB+MC=MG+MB+B′G=BM+MG+GB′>BB′.綜上所述，我們分析出點P到三角形三個頂點A、B、C的距離之和最短.

在這道題目中，利用三角形AMC的旋轉變換將一組“Y”字型的線段巧妙地轉成了兩個定點之間的線段，再通過“兩點之間線段最短”這一理論基礎輕松地證明出P到三角形三個頂點A、B、C的距離之和最短.在教學過程中，對于這類求最值的稍復雜題型，是需要作多條輔助線的，這對學生的能力要求就比較高.在做這一類題目時，首先教師應引入一些簡單圖形的輔助線作法，培養學生作輔助線的意識，同時也訓練了學生的動手能力.其次還應該將作輔助線的題目進行分類，讓學生在腦海里形成清晰的概念，以便拿到相應的題作出相應的圖，從而提高學生的解題效率.

二、運用模型思想―建立方程、函數模型

在解決最值問題時，還有一個常用的方法就是運用模型思想，也就是建立模型，在建立模型時，我們通常會用到方程、函數等的思想，利用均值不等式的計算方法.

例如：已知△XYZ是一個等腰直角三角形，其中直角邊的邊長是1，∠Z=90°.△XYZ的三個頂點分別在等腰三角形ABC的三邊上，其中∠C=90°，求△ABC直角邊長的最大值.

此題只說明了△XYZ的三個頂點分別在等腰三角形ABC的三邊上，并沒有說明△XYZ的三個頂點對應在△ABC的哪條邊上，所以此時的答案就不唯一了，我們需要進行分類討論.

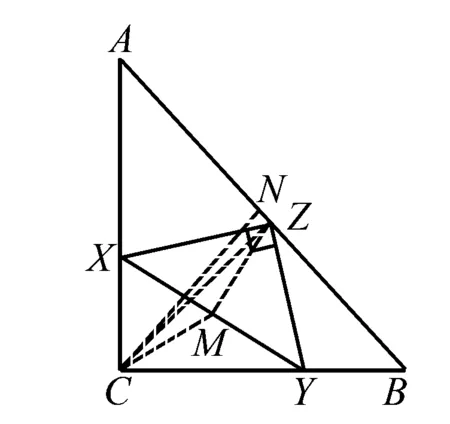
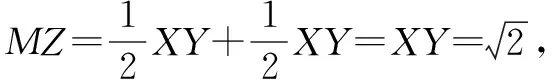
第二種情況：假如△XYZ的頂點Z在△ABC的直角邊上，在這里我們假設Z點在CA上，此時過點Y作YH⊥CA于點H，在這里令CX=x,CZ=y.我們可以知道以下三個條件：ZY=ZX，∠XZC=∠ZYH，∠YHZ=∠XCZ=90°，因此△ZYH全等于△XZC，那么HZ=CX=x,HY=CZ=y，從而進一步可以得到△AHY是等腰直角三角形，于是得出AH=y.

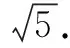
總而言之，在初中數學的教學過程中，核心素養的應用與發展是學生發展的重要途徑之一.因此，教師在數學課堂中，必須圍繞核心素養來展開自己的教學，在教學過程中，教師應多設置情境教學來提高學生的學習興趣、多設置操作環節訓練學生的動手能力等等，總之，一切的目的都是提高學生的學習能力以及綜合發展能力.