關注實驗素養提升──2018年連云港市中考物理卷第20題引發的教學反思

周 嬌

(江蘇省連云港市西苑中學 222042)

相對而言，考試是一種靜態的過程，實驗是一種動態的過程，如何將這兩者有機結合，是近年來中考實驗題的一個出題方向.在實驗題的考核中強調的是學生是否在日常學習中真正經歷了實驗過程，在實驗過程中是否融入了自己的思考.義務教育物理課程作為科學教育的組成部分，是以提高全體學生科學素養為目標的自然科學基礎課程.此階段的物理課程不僅應注重科學知識的傳授和技能的訓練，而且應注重對學生學習興趣、探究能力、創新意識以及科學態度、科學精神等方面的培養.

在目前現行的教學管理中，面臨的是學生人數偏多，實驗教學中總會有學生是渾水摸魚，用著別人的實驗成果完成自己的實驗報告.所以中考這根指揮棒的好好運用，也能讓學生重視平常的實驗參與.2018年連云港市中考物理卷的20題就有效考察了學生是否是通過實驗測得物體運動的速度，并在這一過程中是否融入自己的思考，是否能運用已有的知識去分析問題、解決問題.

一、題目回顧

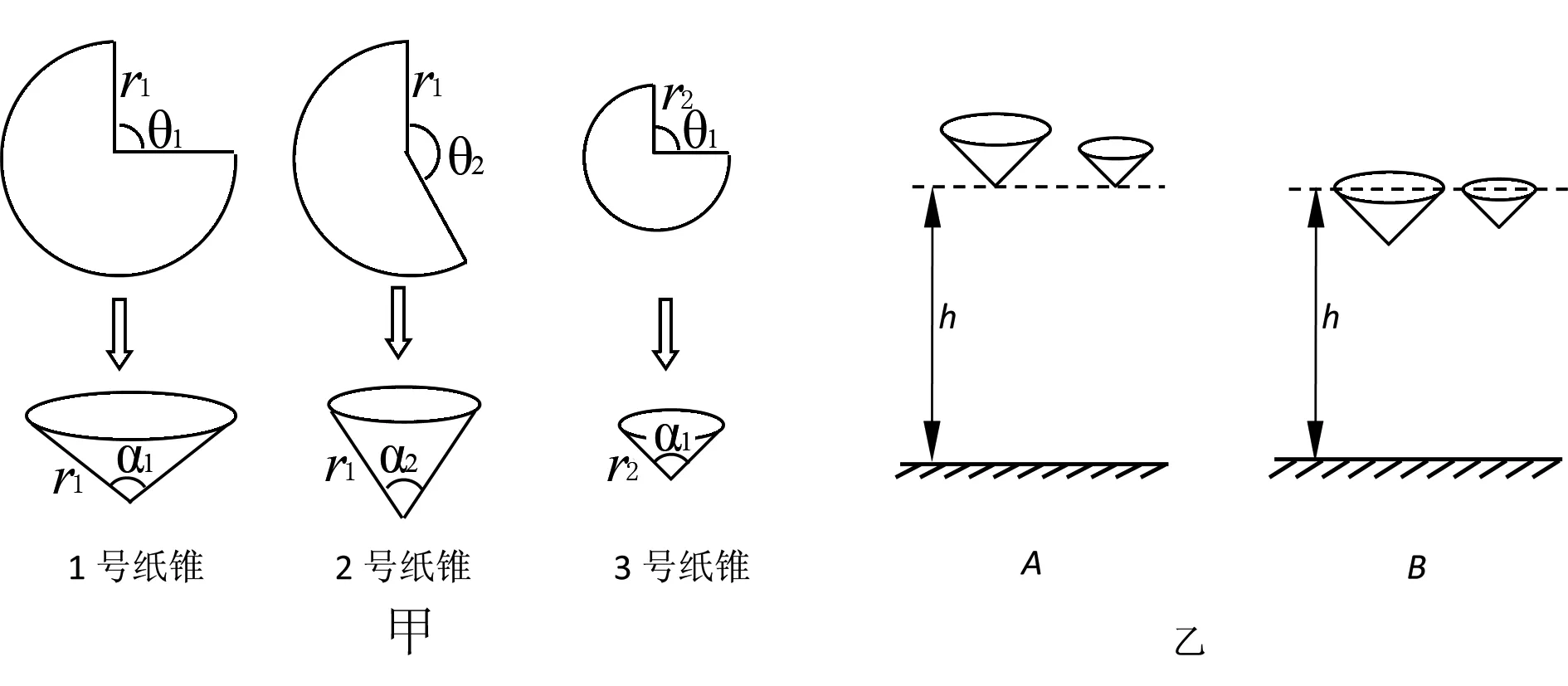
在學習《速度》一節內容后，同學們想探究紙錐下落快慢與錐角以及扇形半徑的關系．他們用普通復印紙裁出3個不同規格的扇形紙片，制成了如圖甲所示的3個紙錐．實驗中，紙錐每次從相同高度由靜止釋放，用秒表多次測量每個紙錐下落的時間，取平均值后記錄在表格中．

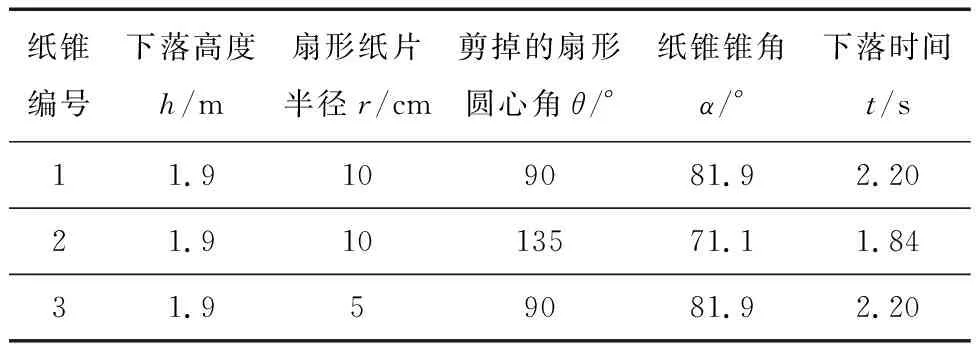
紙錐編號下落高度h/m扇形紙片半徑r/cm剪掉的扇形圓心角θ/°紙錐錐角α/°下落時間t/s11.9109081.92.2021.91013571.11.8431.959081.92.20

(1)對于紙錐下落前的初始位置，有乙圖所示的兩種擺放方式，你認為正確的是 (選填“A”或“B”)．

(2)分析表中數據，根據實驗探究目的，你得出的結論是 ．

(3)小明隨后用同種紙張制成了質量相等的兩個紙錐如圖丙，其中4號紙錐的錐角比5號紙錐的錐角大．如果從相同的高度同時由靜止釋放兩個紙錐，以下選項正確的是 .

A．4號紙錐先到地面

B．5號紙錐先到地面

C．兩個紙錐同時到達地面

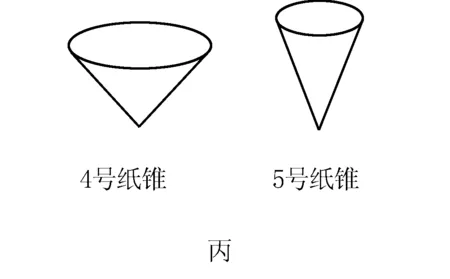
(4)如果紙錐在到達地面前作勻速直線運動，設4號紙錐勻速下落時所受阻力為f1，5號紙錐勻速下落時所受阻力為f2，則f1f2(選填“>”、“<”或“=”)．

二、答題分析

本題的第一問考察的是學生是否經歷了活動“比較紙錐下落的快慢”，以及實驗過程中實驗記錄是否嚴謹.只有認真記錄長度的同學才會關注起點在哪，終點在哪.本題的第二問考察的是學生分析數據以及概括能力.本題的第三問考察的是學生運用第二問的結論分析解決問題的能力.第四問考察的是二力平衡知識，也就是知識的遷移應用能力.

從學生的答題情況來看，第一問中就有學生不知何為初始位置.在第二問中有不少學生是將表格中的信息羅列出來.比如有的同學是這么回答的：下落高度一定時，扇形紙片半徑一定時，剪掉的扇形圓心角越大，紙錐錐角越小，下落時間越短.下落高度一定時，剪掉的扇形圓心角、紙錐錐角相同時，半徑不同，下落時間相同.這時我們可以再回看一遍題目.題目中明確表示：同學們想探究紙錐下落快慢與錐角以及扇形半徑的關系.那根據題目給出的回答應該是紙錐下落快慢與錐角有關，錐角越小，下落越快.與扇形半徑無關.這個答案其實就是從剛才上面同學的回答中提煉出來的.那為什么考試時有些考生只是羅列信息，而不能概括回答呢？如果單從答題來分析，除了常說的審題不清之外，還有一種深層次地的原因應該是學生無從回答.學生在課堂完成的實驗基本是按照教科書完成的，基本上沒有融入過自己的思考.所以當這道題出現時，學生為了得分會盡可能地羅列出來所有信息，至于如何提煉回答，因為平時訓練的機會太少，這個時候恐怕也不敢輕易嘗試.

三、剖析課堂教學改進的基本策略

筆者結合《速度》這一節自己的教學實踐以及聽其他同行的授課情況,談談“比較紙錐下落快慢”這一活動的教學處理情況.

1.常見教學處理方案中隱藏的問題

在這一節教學中紙錐的制作要求如下：剪兩個等大的圓紙片，其中一個圓紙片裁去的扇形的圓心角比另一個大，再分別將它們粘貼成兩個錐角不等的紙錐.本活動的教學中教師通常采取的方式是把紙錐這一制作過程看成一個純粹的手工活，所以要么提供成品材料和詳細要求，以便學生在課堂時間快速制作好.要么教師提前制作完成，課堂提供給學生使用.因為在本節教學中教師特別重視提高學生測量長度和時間的技能以及由此得出速度的定義.所以這一活動只是一個鋪墊，后續主要工作還要放在活動“測量紙錐下落的速度”.也就是在這一教學環節的設計中，我們完全沒有考慮到學生可以有不同的紙錐拿來完成這一活動.也就是我們的教學設置在這一環節完全沒有意識到可以進一步提高學生的探究能力和科學態度的培養.兩個等大的圓紙片，如果讓學生課前自己制作，肯定會出現半徑不等的紙錐，因為書中并沒有對多大提出具體數據要求.并且書中也沒提到做紙錐必須使用的材料，那么學生在選擇材料時未必會選用教師常用的A4紙.但無論是課前教師制作完成，還是課上提供材料，快速完成這一制作過程的做法都限制了學生在這一環節上的創新意識.

2.改進策略

教師進行課堂教學設計時，大部分知識都是以問題的形式引導學生思考而達到知識的建構，所以要促進課堂教學的生成，問題的設置顯得尤為重要.如果問題設置的空間太窄，答案唯一，就不容易有生成，所以問題的設置要注意空間大小適度.在這一活動中我們制作的紙錐，已經能看出錐角小的那個下落快，所以在測量速度這一環節中，我們通常會引導學生選用錐角大的那個測量速度，以便在測量時間時更為準確.其實這個地方是學生的一個興趣點.學生會很樂意比較自己和別人制作的紙錐哪一個下落的更快.由于教師擔心教學整體的時間把握問題，這個比較過程可以放在最后.

比如，教師可以這樣引入：在剛才的學習中，我們測量了自己小組紙錐下落的速度，現在我們再來一個活動，比一比我們不同小組制作的紙錐哪一個下落的更快？這個時候是不能讓學生隨意拿起不同小組的紙錐就開始比較的.那樣的結果只是學生在隨意的玩一個游戲，但這個下落速度和什么因素有關，是完全不知道的.也就是說，我們安排這個活動的目的是想讓學生學會科學的工作方法，而不是簡單地玩一個游戲.為了有序進行，教師可以引導學生限定條件，在學生課前制作時就應提醒學生記下他們剪掉的扇形圓心角的度數.比如請學生拿出剪掉的扇形圓心角為90度的紙錐，這時會發現半徑不等的，材質不同的紙錐都會出現.這時候我們可以提出先選取材質相同的，半徑不等的紙錐作比較，以便我們進行分析.也就是在實際場景中引入了物理重要的一種研究方法：控制變量法.并且多個可能影響因素的出現，也可以訓練學生在總結時如何提煉語言，準確表達出紙錐下落的快慢和哪些因素有關.

實踐活動能使學生學會科學的工作方法嗎？我們當然希望如此，但現實的情況卻是：學生在實驗室所做的實驗與科學家所做的實驗幾乎沒有多少共同之處，學生的實驗只是一系列的照“譜”操作.已經有足夠的證據表明，學生實驗時機械地按照教師(或課本)的要求一步一步去做而不思考，其結果是什么都不會學到，實驗時做過的事情很快就會忘掉，什么也留不住.學生接受的信息必須經過自己頭腦的加工才能留住.

通過以上分析，我們就不難明白，為什么第一問中以紙錐的哪個部位作為初始位置，都能難倒學生.那是因為實驗時這一環節通常由教師提出問題，立馬就有學生做出解答.其他學生跟著照做即可，所以在他們的腦海中很快就會忘記這一注意事項.最后的結論總結工作也是如此，如果只是照本宣科，書上的內容都是現成的.學生會覺得：結論我已經知道，哪里需要我自己費那么多時間再去總結啊.所以筆者認為，教師在處理實踐活動時，一定要適當改變一下實驗的內容和形式，以激發學生的思維興趣.或者說在我們自己的教學實踐中，應該注意挖掘學生深層次的探索興趣.