氣候變化對國家脆弱性影響的計量分析
——以蘇丹為例

徐惠，胡穎

（安徽財經大學，安徽 蚌埠 233030）

氣候變化對世界帶來的一系列影響越來越不容忽視，包括冰川消融、海平面上升、極端氣候、糧食減產甚至物種滅絕等。在對氣候變化研究的趨勢演變背景下，自20世紀90年代起，脆弱性概念開始引入氣候變化影響研究領域。脆弱性概念暴露于風險中的對象是一個多維度復雜系統，涉及自然、經濟、社會、環境等要素。國內外學者相繼在國家和區域尺度上，開展了氣候變化對人類社會各方面的脆弱性評價，并且結合未來經濟以及人口發展情景做出相應預測。

在氣候變化對國家造成影響的問題研究上，Peter Schwartz、Doug Randall 認為氣候的突然變化將使地理政治環境失去穩定性，并對氣候變化給美國國家安全帶來的影響進行了預測[1]。A.I.Kulikov認為生態系統對氣候變暖的反應是干旱和荒漠化，并且貝加爾湖地區生態系統對這種變化的反應速度最快[2]。在對脆弱性問題的研究上，劉葉、賀培從國家的角度，使用因子分析法對金磚5 國的脆弱性進行了比較[3]。任崇強、孫東琪等對中國省域經濟進行脆弱性的綜合評價，拓展了脆弱性研究的新視角[4]。毛亞會、余丹林等則針對城市脆弱性的概念，提出城市脆弱性研究要針對不同研究對象特征進行指標選取和選擇評價方法[5]。綜上所述，學者通常對氣候變化如何影響地理環境、生態系統等進行分析，脆弱性研究的重點集中在不同區域范圍的脆弱性評價體系的建立。而氣候對脆弱性的影響如何進行評價與測度，以及對脆弱性發生改變的預測等方面的研究仍在少數。基于此，本文選取凝聚力、經濟、政治、社會、氣候變化五個指標，建立模糊綜合評價模型，結合典型相關分析法和時間序列模型，以蘇丹為例來度量氣候對國家脆弱性直接和間接的影響，并對其脆弱性的改變作出理論預測。

1 數據來源和假設

本文數據來源于2018年美國大學生數學建模競賽和世界銀行網站。為便于解決問題，本文的研究過程和結論均建立在以下假設成立的基礎上：第一，一個國家的氣候指標可以由年平均溫度、平均降水量、年二氧化碳排放量來完全表示，忽略其他因素對氣候的影響；第二，影響國家脆弱度的指標的選取都是合理的，即凝聚力、經濟、政治、社會、氣候變化可以全面反映一個國家的脆弱度；第三，建立模型的過程中定義的評語等級之間是等距的；第四，本文根據各個指標評分所劃分出的5 個脆弱度等級是合理的；第五，所有數據來源均真實可靠。

2 基于模糊綜合評價模型對氣候影響蘇丹脆弱性的測度

2.1 研究思路

為了刻畫一個國家的脆弱程度，度量氣候因素以直接和間接的方式對一個國家的脆弱性的影響，本文建立了基于層次分析的模糊綜合評價模型。其中氣候因素作為指標體系中的一級指標之一，用以度量氣候對國家脆弱性的直接影響。另外，通過對氣候因素和其他影響國家脆弱度的12 個二級指標進行典型相關分析，來度量氣候對國家脆弱性的間接影響。

2.2 研究方法

2.2.1 模糊綜合評價模型

通過查閱相關文獻，本文選取以下指標對蘇丹的國家脆弱性進行綜合評價，指標的分層結構如圖1所示。

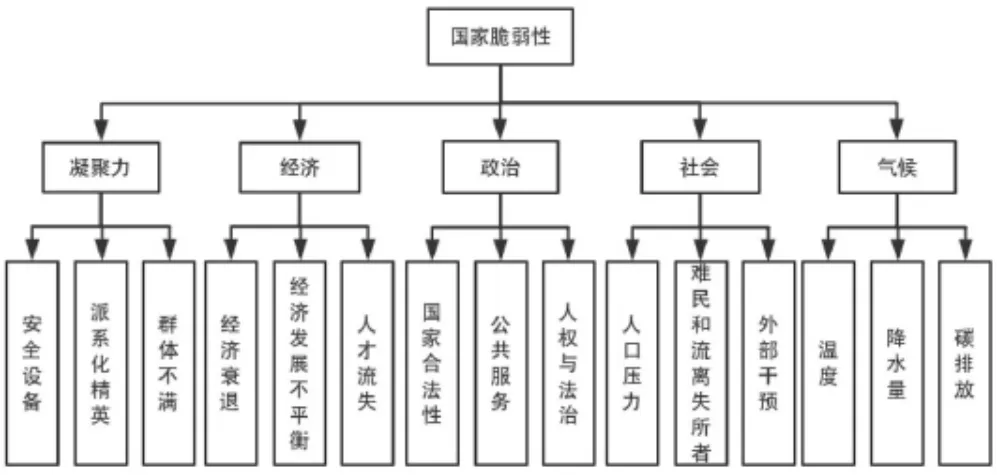
圖1 指標體系圖

采用基于層次分析法的模糊綜合評價模型，對蘇丹的國家脆弱性評價步驟如下。

首先確定因素集，將一級指標設為 A｛A1，A2，A3，A4，A5｝，其中 A1，A2，A3，A4，A5，分別代表凝聚、經濟、政治、社會及氣候變化；二級指標設為 Ai｛ai1，ai2，ai3｝，分別代表每個一級指標下的三個影響因素，其中 i=1，2，3，4，5。其次確定評語集 B｛B1，B2，B3，B4，B5｝，其中 B1，B2，B3，B4，B5分別表示非常脆弱，脆弱，相對穩定，穩定，非常穩定。接著確定各指標Ai隸屬于 B 中評語的 隸屬度 rij(其中 i=1,2,3；j=1,2,3,4,5)，得到評判矩陣 Ri。最后，為了克服完全依靠主觀分析判斷來確定指標權重的片面性，本文采取了層次分析法來計算各層次指標權重，將指標兩兩比較得到判斷矩陣，用 W 來表示 A1，A2，A3，A4，A5五個指標的權重向量，Wi表示各準則Ai(i=1,2,3,4,5)中各指標的權重向量，即 W＝（w1，w2，w3，w4，w5），Wi＝（wi1，wi2，wi3），其中 i=1,2,3。

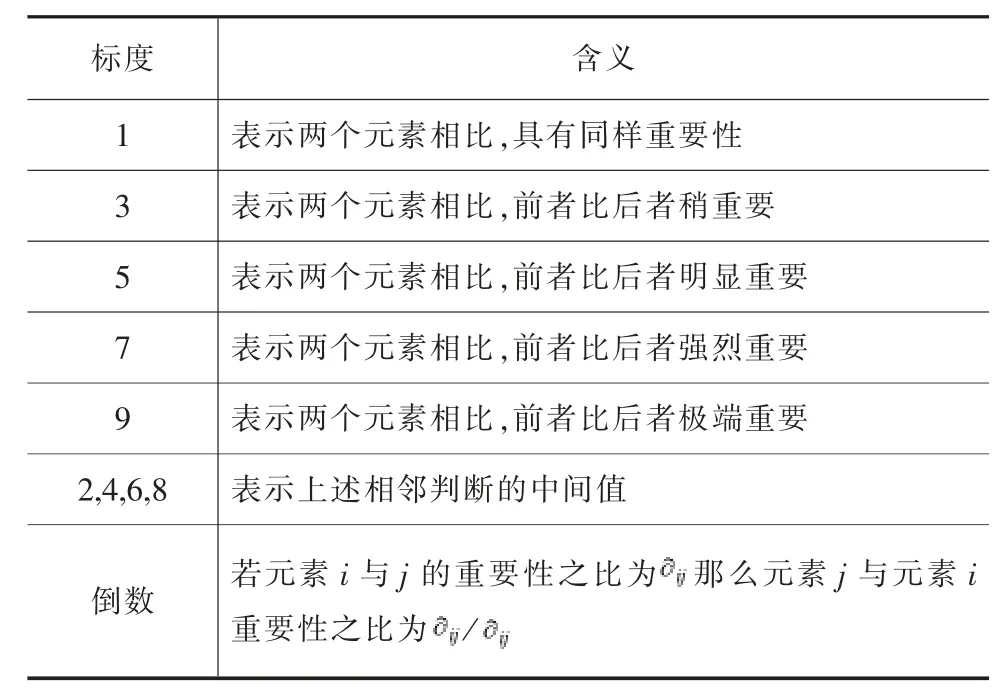
表1 “1-9”標度法

在計算各個指標的權重時，本文借鑒普遍使用的“1-9”標度法，計算結果如表2到表6。

表2 凝聚力指標權重計算結果

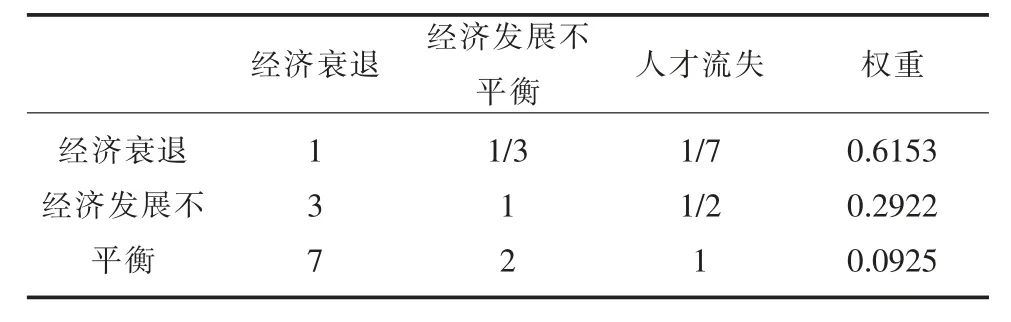
表3 經濟指標權重計算結果

表4 政治指標權重計算結果

表5 社會指標權重計算結果

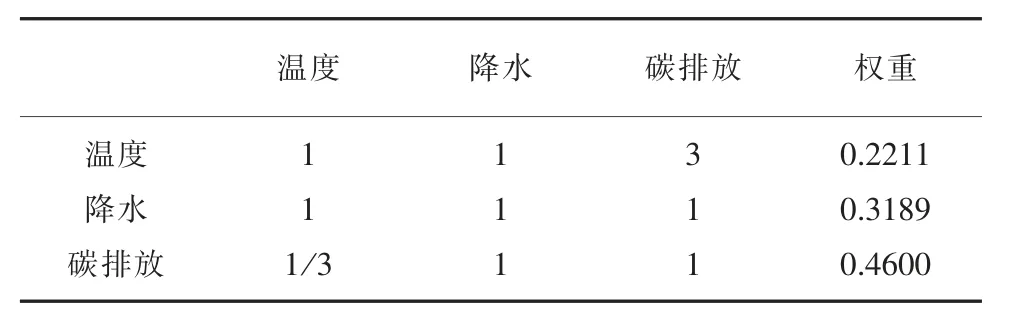
表6 氣候指標權重計算結果

通過計算得到凝聚指標、經濟指標、政治指標、社會指標、氣候指標中影響因素的權重，求出最大特征值分別為3.0385、3.0026、3.0183、3.0092、3.1056；一致性比例分別為0.0331、0.0022、0.0158、0.0079、0.0910。從以上數據可以看出，1-9標度法計算結果通過了一致性檢驗，說明了權重的計算結果是有效的。將結果統一進行歸一化處理，得到最后的評價指標權重向量W=(0.1998,0.1975,0.1985,0.1979,0.2062)，則評語集B＝W.R=（b1,b2,b3,b4,b5,）。對B進行歸一化處理，根據最大隸屬度原則，得到最終的評價結果。

2.2.2 典型相關分析

為了說明氣候變化還可以通過影響凝聚力指標、政治指標、經濟指標、社會指標來間接影響一個國家的脆弱性，本文對氣候指標和上述一系列指標之間做了典型相關分析。

將影響氣候指標的3個因素作為第一組變量，記作（X1,X2,X3），將影響凝聚指標、政治指標、經濟指標、社會指標的12個因素作為第二組變量，記作（Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9,Y10,Y11,Y12）。考慮（X1,X2,X3,）的一個線性組合U以及（Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9,Y10,Y11,Y12）的一個線性組合V，尋找U和V之間盡可能大的相關系數，以充分反映兩組變量間的關系。設

將兩組合并成一組向量

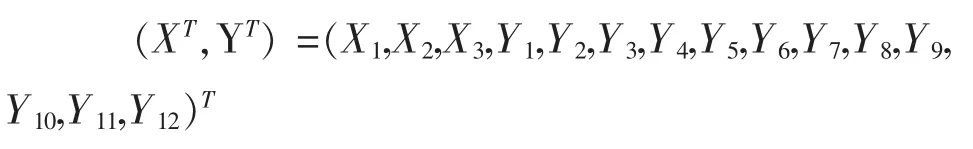
其協方差矩陣為

則線性組合

可使相關系數ρ（U1，V1）達到最大，這里由協方差矩陣，，所以的相關系數為

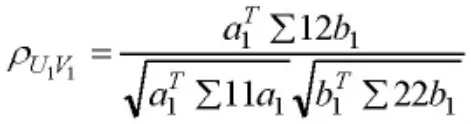
由于相關系數與溫度、降雨量、碳排放量等指標的量綱無關，因此可設約束條件。則滿足此約束條件的相關系數ρ（U1，V1）的最大值就是第一典型相關系數，U1，V1為第一對典型變量。

如果U1，V1不足以反映X,Y之間的相關性，可以構造第二對線性組合：

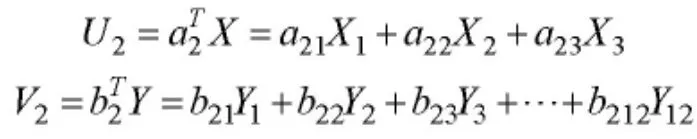
使得（U1，V1）與（U2，V2）不相關，即

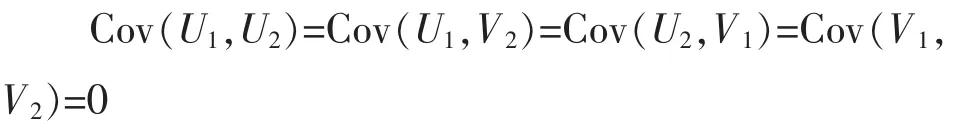
在約束條件Var（U1）＝Var（V1）＝Var（U2）＝Var（V2）下，求出a2，b2使得取得最大值，此時ρU2V2為第二典型相關系數，U2，V2為第二對典型相關變量。

類似地，若前k-1對典型相關變量還不足以反映X,Y之間的相關性，則構造第k對線性組合：

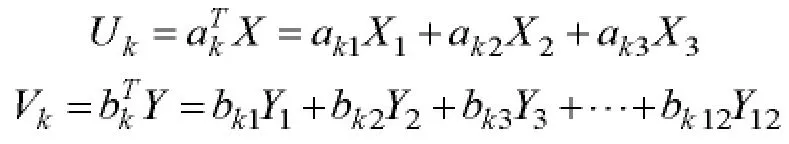
在約束條件

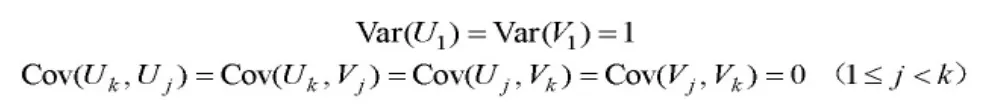
下，求出ak，bk，使得取得最大值，此時為第k個典型相關系數，Uk，Vk為第k 對典型相關變量。按照這種方法，借助相關程序運算，直到找出能夠充分反映兩組指標之間關系的典型相關系數和典型相關變量。兩組指標存在相關性表明氣候可以通過影響其他因素進而影響一個國家的脆弱性。

2.3 結果分析

運用所建立的模糊綜合評價模型對蘇丹的國家脆弱程度做出評價。下圖給出了蘇丹55年來的碳排放量及25年來的溫度和降水變化情況。

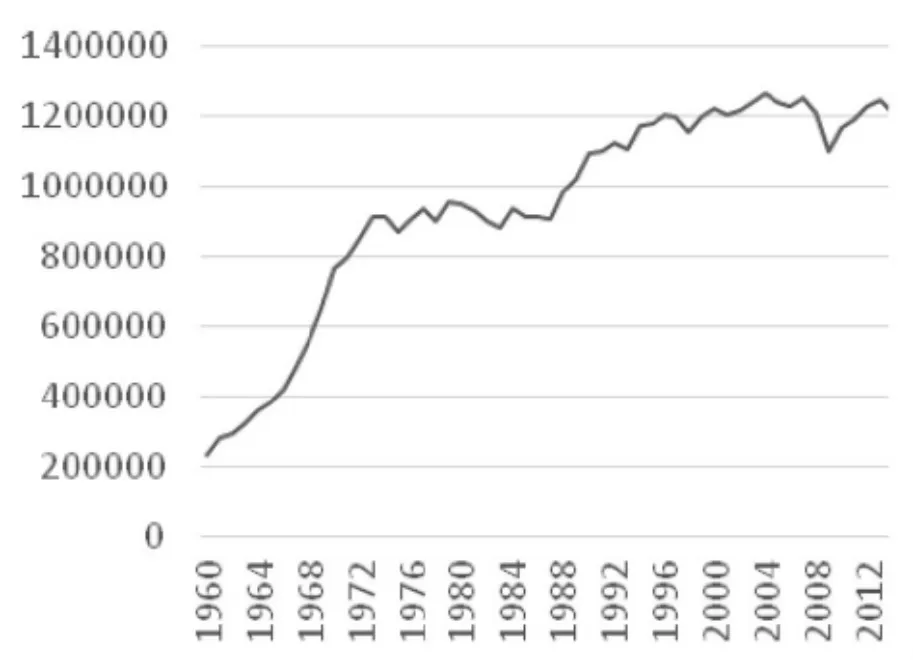
圖2 碳排放量變化折線圖（單位：十噸）

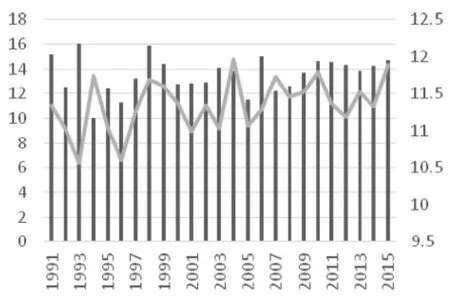
圖3 溫度、降水量變化圖（單位：攝氏度、毫米）

將氣候指標所需數據與其他12個影響因素的評分代入模型，求出其模糊評判矩陣

對矩陣Ra進行合成運算可得Ba=W·Ra=（7.79，7.96，7.72，7.86，7.94）。經過歸一化處理，依據最大隸屬度原則，取數值最大的評語作為綜合評價結果，則評價結果為B2，即蘇丹目前的脆弱程度為“脆弱”。

為衡量氣候因素對蘇丹脆弱性的影響情況，將氣候指標剔除后，用剩余4個指標的12個影響因素重新對模糊綜合評價模型求解，得到其模糊評判矩陣

對矩陣Rb進行合成運算可得Bb=W·Rb=（7.23，7.17，7.28，7.24，7.22）。再對Bb進行歸一化處理，同理可得評價結果為B3，即若不考慮氣候因素的影響，蘇丹的國家脆弱程度為“相對穩定”。由結果可知，氣候變化的直接影響能夠使得蘇丹的國家脆弱性從“相對穩定”變為“脆弱”的等級。

另外，經對兩組變量（X1,X2,X3）和（Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9,Y10,Y11,Y12）進行典型相關分析，得到第一對典型變量的相關系數ρU1V1＝0.6931，可以認為氣候指標與其他影響蘇丹脆弱性的指標之間存在一定的相關性，即氣候因素可以通過影響其他因素進而間接影響國家的脆弱程度。

3 基于ARIMA時間序列模型對蘇丹脆弱性的預測

3.1 研究思路

本文在已經說明氣候能夠對國家脆弱度產生直接和間接影響的基礎上，以1991-2017年蘇丹的溫度、降水量、碳排放量數據為基礎，運用ARIMA時間序列模型對之后幾年氣候的變化進行4 到5步的預測，得出截至2021年每年的氣候數據，將數據重新用于模糊綜合評價模型的求解，得出蘇丹2019年的國家脆弱程度評價結果。

3.2 研究方法

ARIMA 時間序列模型為精度較高的小時間尺度的有效預測模型。該模型可以較好的處理變量隨著時間尺度變化且變量具有相關性的時間序列。由于時間序列預測模型所需數據是平穩的序列數據，因此需將原始氣候數據進行平穩化。通過計算每組數據的自相關函數和偏相關函數，對氣候數據的原始樣本序列進行d 差分運算，將原來的非平穩序列Xt轉化為平穩序列△dXt，假設 p，q 已知，取差分階數d=1，則ARIMA 時間序列模型可用數學形式表示為：

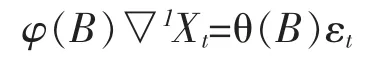
其中，φ 表示 AR 的系數，θ 表示 MA 的系數，Xt表示非平穩時間序列數據，表示預測誤差。

通過AIC 最小的定階準則，對氣候指標下的三個影響因素分別建立合適的時間序列模型，即能夠對氣候的變化做出理論預測。

對碳排放量數據建立ARIMA(0,1,2)模型進行五步預測；對降水量數據建立ARIMA(0,1,1)模型、溫度數據建立ARIMA(1,1,1)模型進行四步預測。使用MATLAB 軟件計算出各模型具體形式如下。

碳排放量預測模型為：

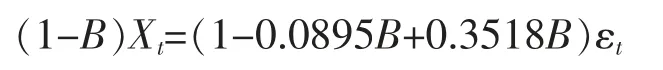
降水量預測模型為：

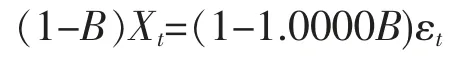
溫度預測模型為：

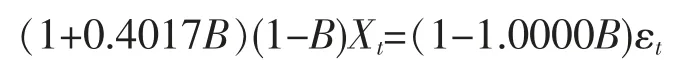
通過MATLAB 軟件求解，得到對氣候數據的四到五步預測結果見表7。

表7 氣候數據預測結果

3.3 結果分析

從時間序列模型的預測結果來看，蘇丹2017-2021年的碳排放量呈遞增趨勢；2018-2021年降水量呈遞減趨勢，而溫度沒有表現出明顯的單調性。預測結果表明蘇丹的氣候在未來幾年可能出現惡化，因此本文將預測所得數據重新用于評價蘇丹的國家脆弱性，探究氣候的惡化將如何影響蘇丹未來的脆弱程度。

將預測所得的氣候因素數據再次運用到模糊綜合評價模型，求出其模糊評判矩陣

和 Bc=W·Rc=（7.86，7.80，7.84，7.60，7.50）。同理依據最大隸屬度原則，其評價結果為B1，即此時蘇丹的脆弱程度為“非常脆弱”。

對比氣候預測前的模型評價結果，可以看出由于氣候變化的影響，例如碳排放量增多，溫度升高和降水過多或過少等因素，使得蘇丹的脆弱性在2021年轉變為非常脆弱。

4 結語

本文以蘇丹為例，通過構建影響國家脆弱性的指標體系，基于模糊綜合評價模型、典型相關分析法、ARIMA 時間序列模型來度量氣候變化對國家脆弱性的影響，得到結論：第一，若不考慮氣候因素的影響，當前蘇丹的脆弱程度為“相對穩定”，而將氣候因素考慮后，蘇丹的脆弱程度為“脆弱”。第二，氣候的惡化將加劇國家脆弱性，可能導致蘇丹的脆弱程度在2021年由“脆弱”變為“非常脆弱”。因此，氣候因素不僅會對生態環境造成巨大損害，而且能夠通過直接和間接的方式影響國家的脆弱程度，為國家安全、社會穩定造成了一定的威脅。

本文建立的多層次的模糊綜合評價法能夠把定性方法與定量方法有機結合，很好的處理國家脆弱性這一模糊的評價對象，做出比較科學、合理、貼近實際的量化評價。但由于影響國家脆弱性的指標和因素繁多，現有指標體系無法保證將所有的影響因素全面考慮。另外本文僅以蘇丹為例進行實證分析，因此模型在不同國家和地區的運行能力還有待檢驗。