基于ARIMA模型對我國農村人口的預測分析

官 銀，李新月，朱家明

（1.安徽財經大學會計學院，安徽 蚌埠 233000；2.安徽財經大學統計與應用數學學院，安徽 蚌埠 233000）

引言

隨著我國經濟的高速發展，人口的流動速度越來越快，越來越多的年輕人選擇在大城市發展，從而導致我國農村人口的數量急劇下降[1]。農村人口變遷和其生產、組織、社會保障等問題密切相關，而農村的發展好壞直接關系著我國總體的發展水平，農村好的發展離不開足夠的勞動力[2]。因此，對我國農村人口未來變化的預測與分析是十分有必要的，通過觀察其未來的人口變化趨勢，可以為政府等相關部門提供制定相關政策的依據。

目前，預測的方法有很多種，如：灰色預測、指數平滑法、線性回歸預測等，這些方法都有其各自的優勢。但是，對于時間序列數據目前最常用的并且也最準確的就是ARIMA 模型預測和ARMA 模型預測。其中，ARMA 模型預測主要用于平穩性時間序列預測，ARIMA 模型預測主要用于非平穩時間序列預測。因此，在使用前都需要對時間序列進行平穩性分析，然后再選擇用哪一種方法進行預測分析。但是，即使是ARIMA 模型最終還是回歸于ARMA 模型，在對非平穩時間序列數據進行若干次差分之后，數據將會變為平穩性數據，此時仍然是做出自相關圖和偏自相關圖從而確定模型的參數p 和 q，ARIMA 模型的建模基本步驟[1]見圖1，主要有：數據的平穩性檢驗、模型的識別與定階、參數估計、模型適應性檢驗、模型誤差分析和模型預測六個方面。

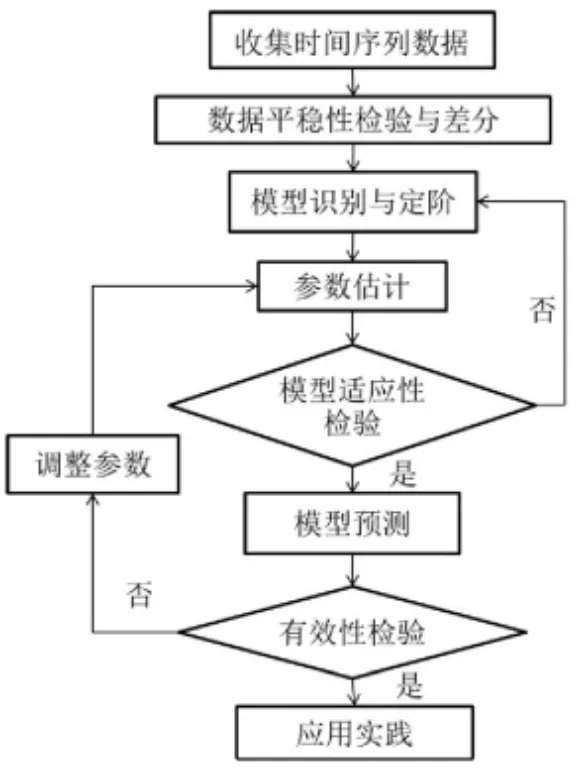
圖1 ARIMA 模型建模步驟

1.文獻綜述

趙華、薛紅艷[3]指出預測人口數量對引導適當人口規模的重要性，在文章中對河北省1952-2010年總人口數據進行分析，得出河北省在此期間人口數量呈持續上升狀，且其原始序列數據是非平穩的。為消除原始序列數據趨勢并降低其波動性，文章針對原序列數據進行一階逐期差分處理，經過檢驗大致消除了原序列趨勢。運用此模型預測該省2013-2017年人口數量，得出河北省人口數量將持續增長的結論。

鄭紅云[4]根據深圳市1979-2010年常住人口數據進行了 ARIMA（1，1，0）模型擬合，得出未來十年深圳市常住人口的預測數據，并運用ARIMA（1，0，0）擬合了深圳市 1979-2010年常住人口中每千人床位數，擬合效果較好。預測結果表明，預期該市今后十年的常住人口量超過1300 萬人，且該市每千人床位數將持續位于較低狀態，而市民將需要繼續面臨較大的就醫壓力。

鄭小鳳，沈姮等[5]在文章中簡要介紹了時間序列分析對動態數據預測的重要性，通過分析我國2013年底總人口數情況，利用Stata 軟件進行單位根檢驗，確定所用序列具有平滑性。在此基礎上建立ARIMA 模型，對2014年和2015年中國人口數進行預測，得出我國人口增長總體態勢較平穩的結論。

郭敏，田薈等[6]對ARIMA 方法進行了簡要介紹，并結合歷年來人口政策對我國1950-2016年人口出生率進行分析。借助EVIEWS 軟件與ARIMA建模方法，將ARIMA 模型運用到我國人口出生率預測中，根據不同模型SC 和AIC 的值，識別確定選取ARIMA(0,1,2)模型，依此預測我國2018年人口出生率約為13.06%，可為我國政府政策制定提供參考。

根據以上研究，可發現時間序列模型在人口數量分析中備受青睞。本文以全國農村人口為總體建立ARIMA 模型，對未來農村人口數量進行預測研究，以期為政府制定相關政策提供一定判斷依據。

2.數據來源與描述性統計分析

本文所用到的1970~2015年中國農村人口數量數據均來自于世界銀行公開數據庫。為了對數據的總體情況有一個大概的了解，本文將數據進行了描述性統計分析，具體結果見表1。

表1 1970～2015年中國農村人口數據描述性統計分析單位：萬人

通過統計分析可以看出我國農村人口的均值為76612.8 萬人，最多的時候達83647.9 萬人，最少的時候達60862.9 萬人，可以看出我國農村人口的數量變化較大。

同時，做出1970~2015年我國農村人口的時序圖，見圖2。通過時序圖可以看出我國農村人口先迅速增長，到了20 世界90年代開始逐年下降。

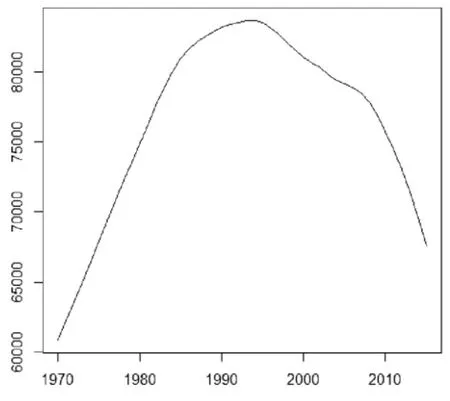
圖2 1970～2015年中國農村人口時序圖

3.ARIMA模型的建立與求解

3.1 數據平穩性檢驗與預處理

通過圖2可以明顯看出我國農村人口的變化數據是不平穩的，對于非平穩的時間序列，可以采用差分的方法將其變成平穩的時間序列數據。首先可以利用公式（1）對其進行一階差分，如果一階差分之后，數據仍然為非平穩數據，則利用公式（2）對其進行二階差分，以此類推直到數據變為平穩的時間序列數據。

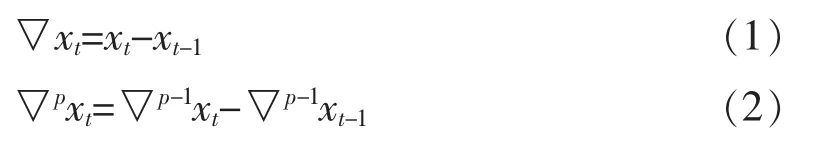
為了更具有說服力，首先對原始數據進行ADF檢驗[8-9]，計算結果見表2。

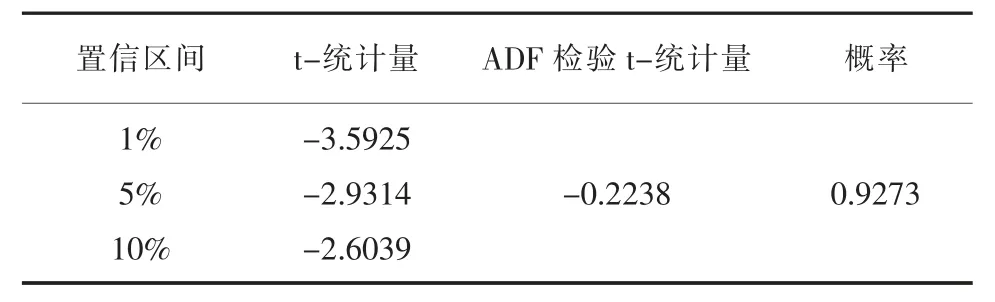
表2 原始數據ADF 檢驗表

通過ADF 檢驗可以看出t-統計量在0.1 置信區間之外并且P 值為0.9273 遠大于0.05，因此可以看出原始數據的確為非平穩數據。接下來，對原始數據進行一階差分，并對差分后的數據進行ADF檢驗，具體結果見表3。

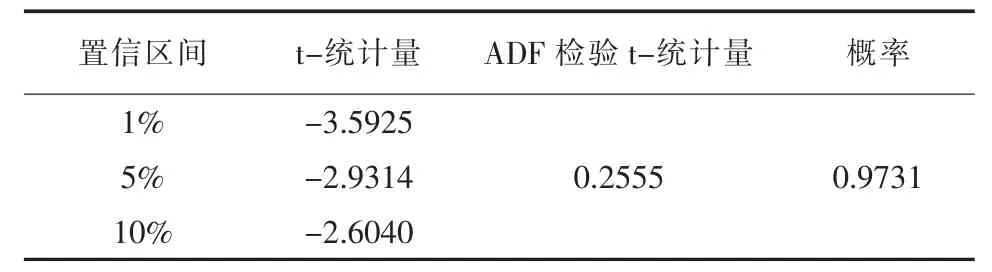
表3 一階差分后數據ADF 檢驗表

通過表3可以看出一階差分后的數據仍然為非平穩數據。接下來，對其進行二階差分，二階差分后繼續進行ADF 檢驗，得到的檢驗結果見表4。

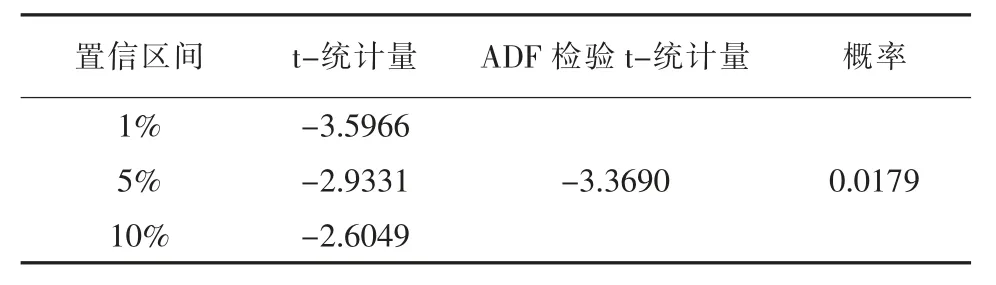
表4 二階差分后數據ADF 檢驗表

通過檢驗結果可以看出二階差分之后的數據為平穩性數據，P 值為0.0179 小于0.05。與此同時，繪制出二階差分后的中國農村人口時序圖 （見圖3），可以直觀地看出二階差分后數據為平穩的。因此，可以確定參數d 的值為2。

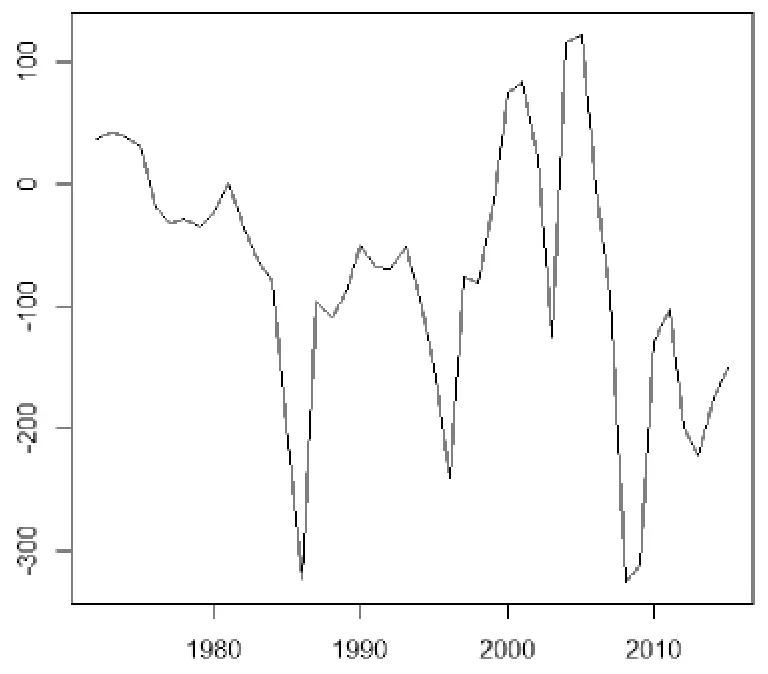
圖3 二階差分后時序圖

3.2 ARIMA模型識別與定階

繪制二階差分后的時間序列的自相關圖（ACF）和偏自相關圖（PACF）初步識別 p，q 的值。通過圖4可以看出，ACF 第一階后呈截尾狀。通過圖5看出，PACF 第一階后呈拖尾狀，因此可初步判定差分后的序列適合ARIMA（1,2,1）模型。

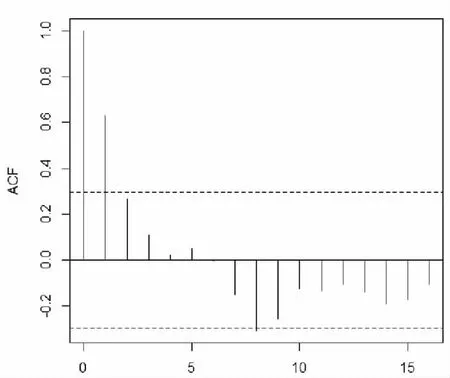
圖4 序列自相關圖

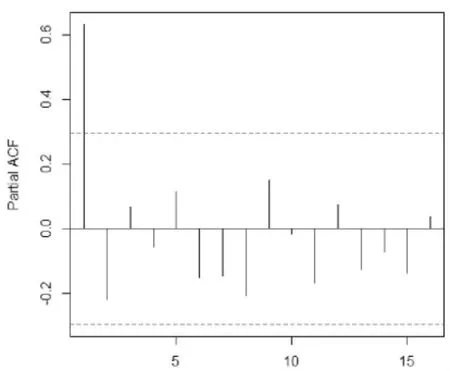
圖5 序列偏自相關圖

3.3 時間序列模型參數估計

重復擬合ARIMA（p,d,q）模型中的參數p 和q的各種可能取值，并計算相應參數對應的AIC 值和BIC 值來初步判定模型的最佳階數，計算結果見表5。

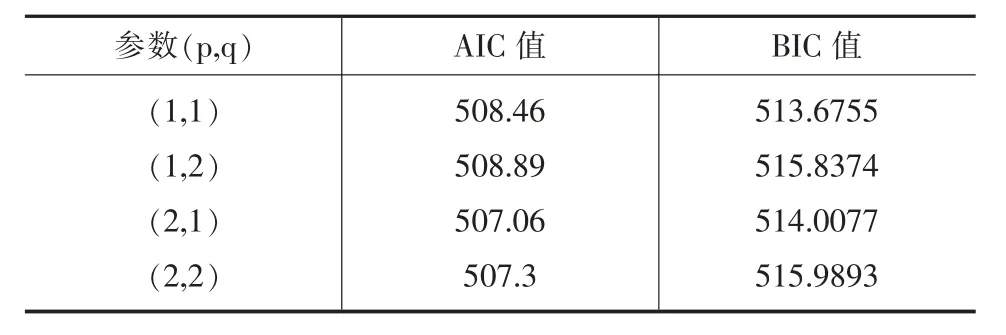
表5 農村人數的AIC 值和BIC 值

通過觀察表5的計算值，可以看出參數（1,1）使 BIC 的值最小，參數（2,1）使 AIC 的值最小。因此進一步比較他們的擬合效果，對參數 （1,2,1）和（2,2,1）對應的模型分別作出模型的擬合圖（見圖6和圖7）。

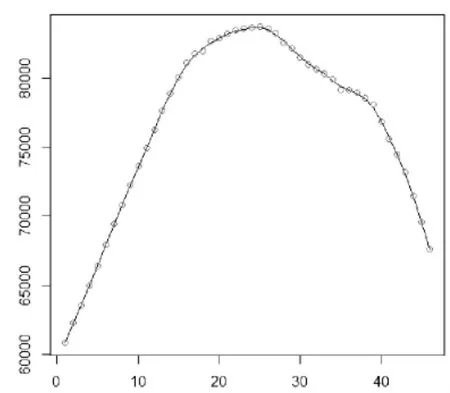
圖6 ARIMA（1,2,1）擬合曲線

通過比較 ARIMA（1,2,1）和 ARIMA（2,2,1）模型擬合的結果，看出兩者相差不大，擬合結果幾乎一樣。因此，在這里無法判斷ARIMA（1,2,1）和ARIMA（2,2,1）模型哪一個更好，再繼續對其做相關的檢驗。

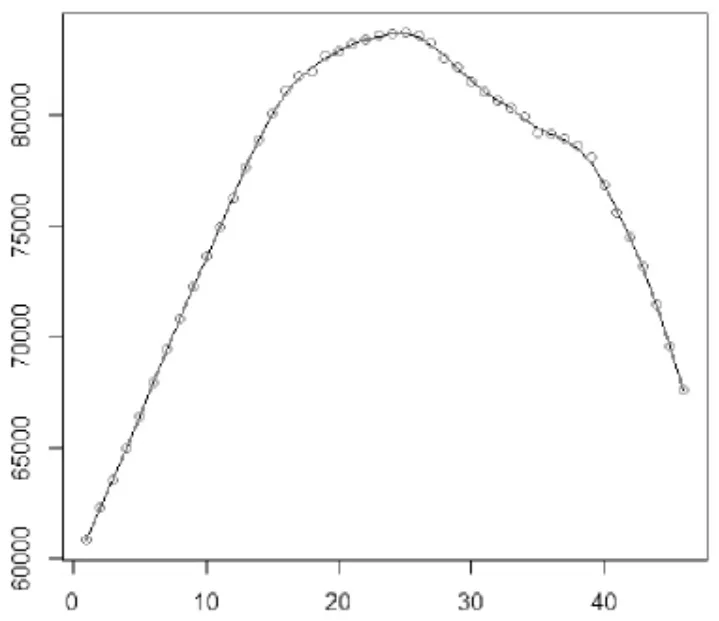
圖7 ARIMA（2,2,1）擬合曲線

3.4 ARIMA模型的適應性檢驗

為了得到模型的適應性，模型殘差序列進行白噪聲檢驗，得到它們的殘差序列圖見圖8和圖9。與此同時進行了Box 檢驗，得到ARIMA（1,2,1）在6階延遲和12 階延遲下 p 值為 0.8285 和 0.7192，得到 ARIMA（2,2,1）在 6 階延遲和 12 階延遲下 p 值為0.9119 和0.8425，說明殘差為白噪聲序列，建立的ARIMA 模型是適用的。

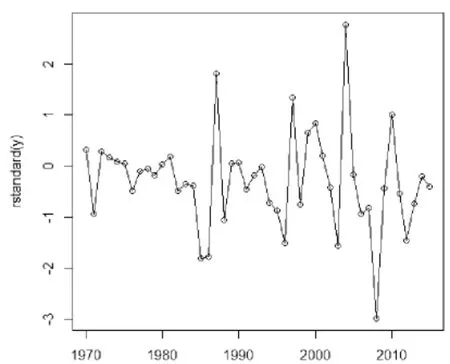
圖8 ARIMA（1,2,1）模型殘差序列圖

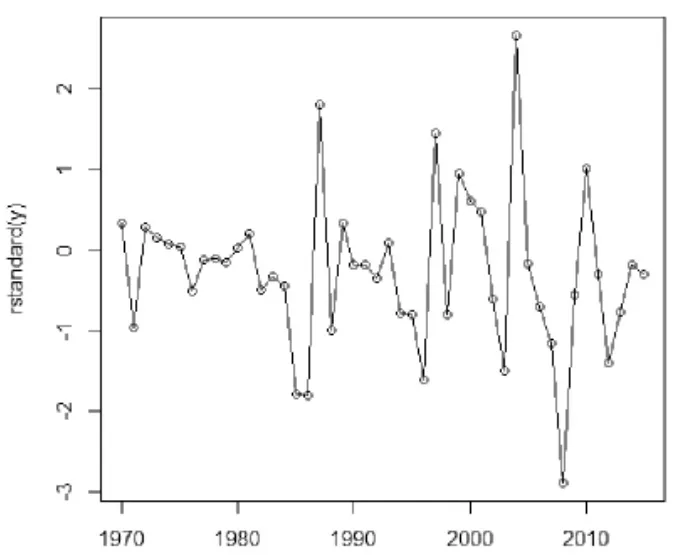
圖9 ARIMA（2,2,1）模型殘差序列圖

4.ARIMA模型預測與誤差分析

4.1 ARIMA模型誤差分析

分別對 ARIMA（1,2,1）和 ARIMA（2,2,1）模型進行誤差分析，選用平均絕對誤差（MAE）、均方根誤差（RMSE）和平均絕對百分誤差（MAPE）作為評估模型效果的標準。

MAE、RMSE、MAPE 的表達式分別為：

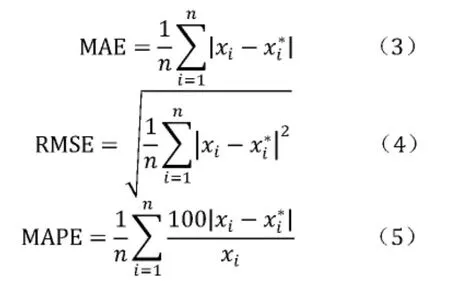
通過計算結果 （見表6）可以看出，ARIMA（1,2,1）比 ARIMA（2,2,1）模型稍好，誤差相對較小，因此最終選定ARIMA（1,2,1）模型對我國的農村人數進行預測。

表6 不同參數對應模型誤差

4.2 ARIMA模型預測

利用得到的ARIMA（1,2,1）模型對我國未來十年的農村人口進行了預測（見圖10），為了更加精確的看出預測結果，將得到的預測結果做成表格見表7。通過預測結果，可以看出我國農村的人口數量逐年減少，農村人口嚴重流失。這也與我國真實的情況相符，越來越多的人離開了農村，導致我國農村人口大量流失。

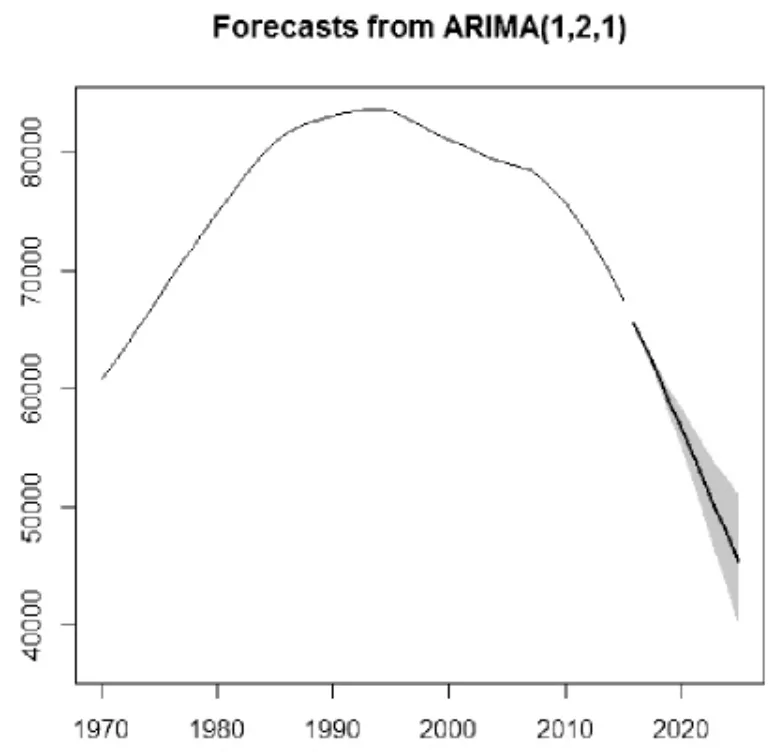
圖10 ARIMA（1,2,1）模型預測結果

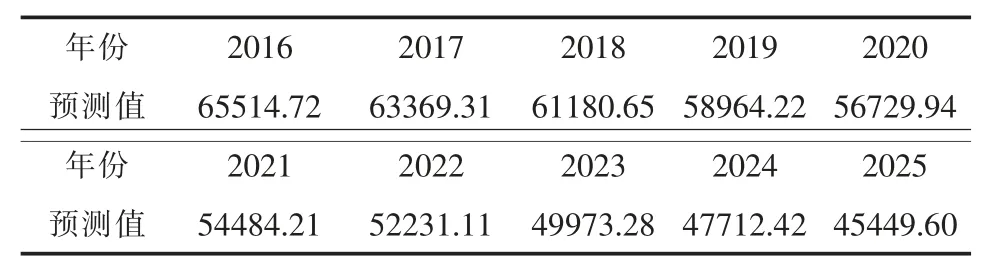
表7 未來十年我國農村人口預測數量

5.結論與政策建議

本文建立了ARIMA 模型對我國的農村人口進行預測，通過數據的平穩性檢驗、模型的識別與定階、參數估計、模型適應性檢驗和模型誤差分析五個步驟確定了ARIMA 模型的三個參數，最終選擇了ARIMA（1,2,1）模型對數據進行擬合以及預測。根據預測結果可以看出我國未來的農村人數呈現逐年下降的趨勢，這可能會讓我國的農村勞動力嚴重下滑，對未來的發展產生深遠影響[10]。

基于上述結論，對于我國農村人口數量發展給出以下政策建議：

第一，對農村勞動力涌向城市的過程進行規范與引導。在農村勞動力的轉移過程中，提高其轉移有序性，避免發生農村耕地無人照料而城市農民工過剩的現象。

第二，對農村人口發展現狀進行實地調研，適時適度對我國人口政策進行調整，為城市和農村勞動力的平穩有效供給提高保障。

第三，提高政府支持力度。一方面，完善三農政策。鼓勵和號召更多的農民留在農村，吸引那些常年在外工作具備經驗和膽識的農民回村，為農村建設添磚加瓦。另一方面，政府可出臺相關政策鼓勵高技術人才加入農村建設中，保證其工作條件，為其提供一片廣闊天地大展身手[11]。

第四，大力發展農村生產力，加速農業現代化發展進程。國家應制定相關政策提升農業科技水平，讓機器代替手工勞動，修繕農村相關水利設施，為農村發展和農民生活謀福。此外，應注重引導適量的規模化企業往農村農業投資，給農業可持續發展鋪好道路。

因此，政府等相關部門應該盡快制定相關的政策，減少農村人口的流失，讓我國的農村保持競爭力和活力。