一種用于準單站配置的步進頻探地雷達建模方法

張經緯 劉 新 葉盛波 方廣有*

①(中國科學院大學 北京 100049)

②(中國科學院電子學研究所 北京 100190)

③(中國科學院電磁輻射與探測技術重點實驗室 北京 100190)

1 引言

探地雷達作為一種高效的無損檢測工具，在國防、考古、地質勘探、道路與橋梁檢測等方面具有十分廣泛的應用[1-4]。探地雷達的回波信號解釋方法可以分為兩類，一類是從信號中識別反射脈沖的幅值和時延，然后依據簡化的傳播模型對被檢測媒質的厚度和介電常數進行反演[5]；另一類是先對雷達信號在被檢測媒質中的傳播過程進行物理建模，然后利用最優化方法對回波信號進行全波反演，得到媒質的介電常數和厚度[6]。全波反演方法是從物理角度出發模擬雷達回波信號的產生機理，因此能獲得更高的檢測精度。傳統的探地雷達建模方法對雷達信號的傳播過程作了較強的簡化假設，尤其是在建模過程中忽略了天線對雷達信號的影響，包括天線的輻射模式、增益、傳播時間、色散以及天線與媒質間的相互作用等。

為了準確模擬天線系統對雷達信號的影響，許多研究人員采用數值方法對探地雷達系統進行建模，包括時域有限差分方法(FDTD)[7，8]、有限元方法(FEM)[9]、矩量法(MOM)[10]等。這些數值方法的優勢在于能夠處理各種復雜的媒質結構，并且不需要對被檢測媒質做過多的簡化假設。但是數值建模方法的劣勢在于計算效率低，這使得它們在需要對正演模型進行大量的重復計算的全波反演方法中不適用。探地雷達系統在特定的應用場景下也可以利用解析方法進行建模，如針對平面分層媒質的檢測。在眾多的解析建模方法中，基于電場積分方程的方法是最有前景的。例如，Gentili和Spagnolini采用與頻率無關的電偶極子陣列對喇叭天線進行建模[11]，但是在該模型中，沒有考慮雷達信號在天線口面與媒質之間的多次反射。Lambot等人[6]針對單站配置(收、發天線重合)步進頻探地雷達系統提出了一種建模的方法，該方法在平面分層媒質中的雷達回波模擬和介電參數反演等方面有著出色的表現。由于常用的探地雷達系統都采用準單站配置(收、發天線分離但離得較近)，本文基于單站配置探地雷達的建模思想提出了一種用于準單站配置的步進頻探地雷達正演模型。在該正演模型中，發射天線和接收天線被等效為水平電偶極子，天線對雷達信號的影響以及天線與分層媒質間的相互作用被表示為只與頻域有關的傳輸函數。為驗證提出的正演模型的建模精度，本文在實驗室條件下利用矢量網絡分析儀和喇叭天線搭建了步進頻探地雷達系統，并依據正演模型對從厚度已知的石膏板和木板測得的雷達信號進行全波反演。為進一步比較準單站配置和單站配置的探地雷達系統的反演性能，本文利用石膏板、木板和金屬板構建了3層結構模型，并對兩種配置的探地雷達在3層結構中得到的回波信號進行了全波反演。通過對反演結果分析，證明了準單站配置探地雷達因其具有更高的信噪比而具有更好的反演性能。

2 探地雷達建模及全波反演

2.1 單站步進頻探地雷達建模

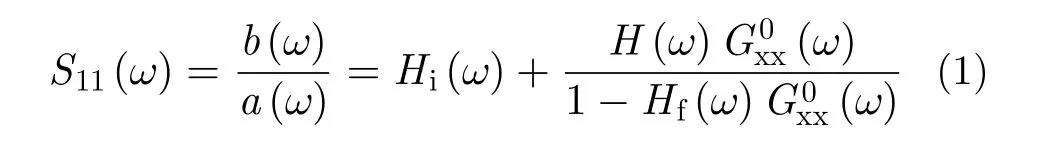
2.2 準單站探地雷達正演模型

本文提出了一種用于準單站配置的步進頻探地雷達的正演模型。考慮到在準單站配置中，發射天線與接收天線間的偏置較小，因此在遠場條件下接收天線處測得的電場可以作平面波近似，同時在正下視方向上天線的增益只與頻率有關。在該假設條件下，發射天線與接收天線可以分別用一個位于天線口面中心處的水平電偶極子近似；其中天線的增益、相位延遲、收發天線間的互耦以及天線與分層媒質間的相互作用可以用一組只與頻率有關的傳輸函數表示。依據這些假設，本文提出了按照圖1所示的系統框圖對準單站步進頻探地雷達進行建模。根據圖1所示，步進頻探地雷達的信號可以表示為

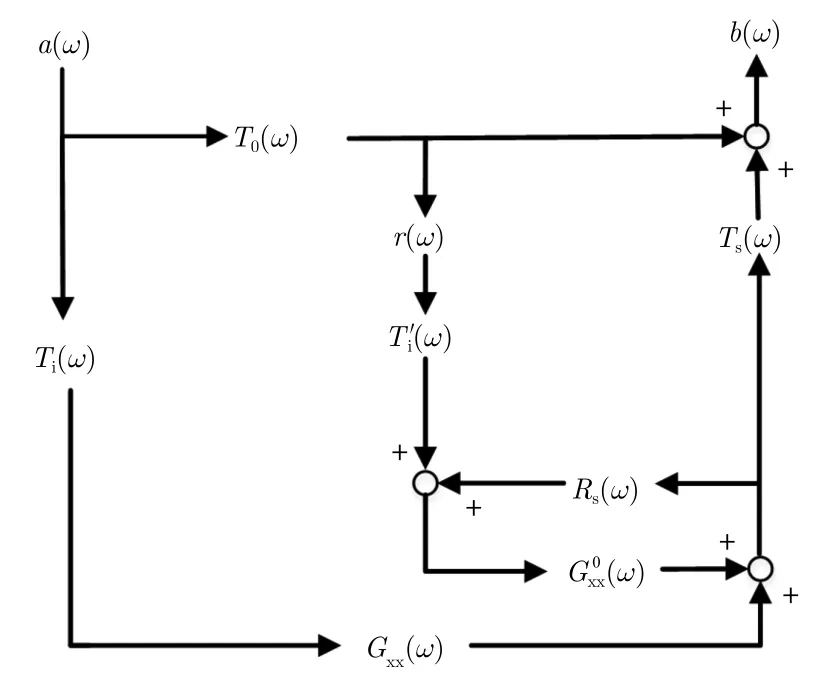
圖1 準單站探地雷達建模框圖Fig. 1 Modeling diagram for the quasi-monostatic ground penetrating radar

因此線性方程組可以表示為以下矩陣形式：

其中

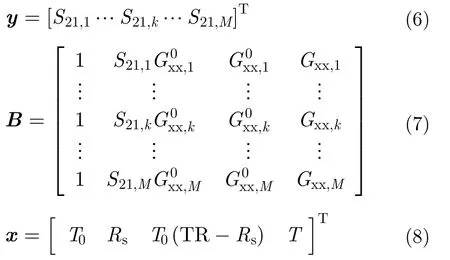
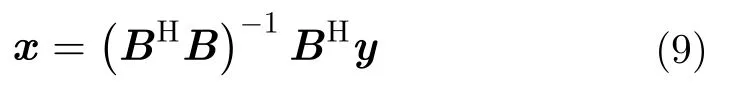
其中，H表示共軛轉置操作。

2.3 全波反演

3 模型校準和驗證

3.1 模型校準

本文利用便攜式矢量網絡分析儀模塊S5048[13]和2個喇叭天線搭建步進頻探地雷達系統。其中，矢網的工作頻段為0.9～4.0 GHz，共256 個頻率點，中頻帶寬為3 kHz，在測試前矢網經過校準件進行校準。喇叭天線長24 cm，口面尺寸為16 cm×30 cm，有效帶寬為0.8～8.0 GHz。2個天線呈E面平行放置，天線口面中心點相距20 cm。為了得到正演模型的傳輸函數，利用該雷達在一個2.5 m×2.5 m大的金屬板上方0.48～0.75 m高度范圍內進行55 次不同高度的測量，如圖2所示。為了量化建模誤差，可以定義一個建模誤差函數：

圖2 準單站配置和單站配置探地雷達系統Fig. 2 Configurations of quasi-monostatic and monostatic GPR

其中，y是各個高度下金屬板實測信號，是各個高度下金屬板實測信號的最優逼近值，是傳輸函數的最小二乘解。為了驗證模型中的參量的作用，可以通過將式(2)中的置零，得到一個簡化的模型：

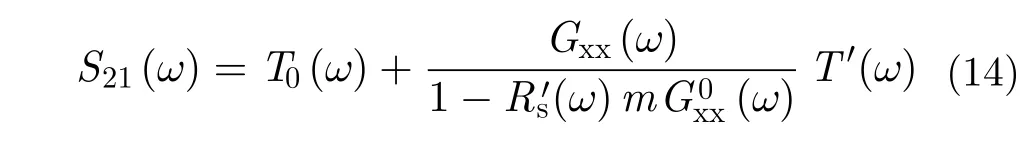
利用同樣的雷達測量數據可以對上述簡化模型的傳輸參數進行求解。圖3展示了參數簡化模型和原始模型在各個頻率上的建模誤差。結果表明，去掉模型參量后，雷達系統的建模誤差會上升，因此在模型中考慮參量的貢獻對提升探地雷達系統建模的準確度是十分重要的。

3.2 模型驗證

圖3 簡化模型和原始模型建模誤差Fig. 3 Fitting errors of the simplified model and original model

為驗證提出的正演模型的準確度，本文利用搭建的探地雷達系統分別在厚為28.4 mm面積為1.6 m×1.8 m的石膏板和厚度為19.0 mm面積為1.8 m×2 m的干木板上方不同高度處進行測量，并且用一個面積為2.5 m×2.5 m的覆銅板用來充當底部的邊界條件，如圖4所示。在對測得的雷達信號進行參數反演時，假定石膏板和干木板的介電常數與頻率無關，且兩者的電導率均可忽略。圖5(a)和圖5(b)分別展示了利用反演參數得到的仿真波形和實測波形，從圖中可以看出利用反演結果得到的仿真波形和實測波形具有很高的吻合度。

表1和表2分別展示了對石膏板和干木板的雷達測量波形進行全波反演得到的結果。

圖4 利用厚度已知的石膏板驗證準單站探地雷達模型的精度Fig. 4 Validating the accuracy of the quasi-monostatic model with the thickness-known plasterboard

在表1中，反演得到的石膏板的平均相對介電常數為2.32，標準差為0.006。在表2中，反演得到的木板的平均相對介電常數為2.73，標準差為0.009。石膏板和木板的最大厚度反演誤差均為0.3 mm。在表1和表2中反演得到的介電常數的值都比較穩定，且對應的反演厚度誤差都非常小，因此利用反演得到的相對介電常數的平均值代表其真實值是合理的。表1和表2的反演結果說明本文提出的準單站步進頻探地雷達的正演模型具有很高的精確度。為了進一步驗證，在原始模型中考慮參數r(ω)能夠提升模型的精度，本文利用簡化模型對同樣的石膏板測量數據進行了全波反演。表3中為利用簡化模型反演得到的石膏板參數。對比表1和表3的結果可知，由簡化模型反演得到的石膏板的介電常數略微大于原始模型得到的介電常數。這是因此，利用簡化模型進行全波反演時，實際由原始模型中參數對反射波形產生的部分貢獻也被錯誤地歸因于簡化模型中的其他參數，導致簡化模型中得到的石膏板反射波形比實際石膏板的反射波形強度大，即等效反射系數大，而在進行全波反演時，利用的是最小化均方誤差的優化準則，因此最終通過最優化方法反演得到的石膏板介電常數也會略大于真實值。

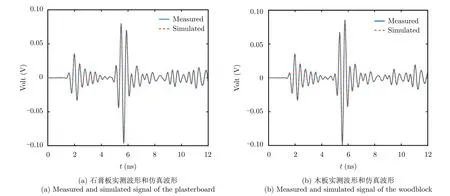
圖5 石膏板與木板的實測波形與仿真波形的對比Fig. 5 Comparison of the measured and simulated signal for plasterboard and woodblock

表1 準單站探地雷達石膏板反演結果Tab. 1 Inversion results of the plasterboard with the quasi-monostatic GPR

表2 準單站探地雷達木板反演結果Tab. 2 Inversion results of the woodblock with quasi-monostatic GPR

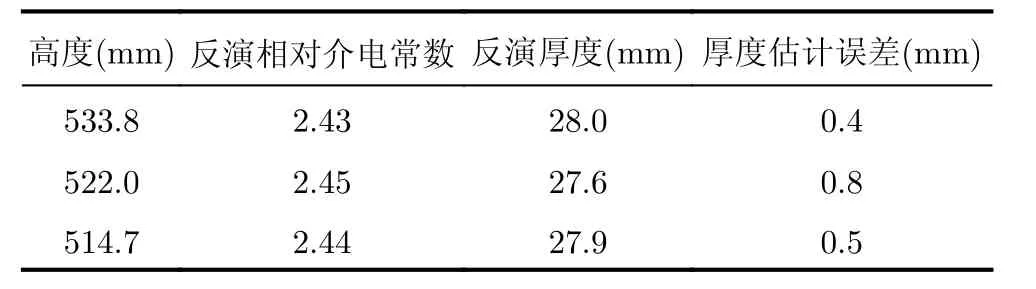
表3 簡化模型對石膏板的反演結果Tab. 3 Inversion results of the plasterboard with simplified model

4 準單站配置與單站配置探地雷達性能對比

根據前人的研究成果和本文的實驗結果表明，單站配置和準單站配置步進頻探地雷達系統都能被精確地建模，且能獲得良好的反演性能。為了進一步比較準單站配置和單站配置探地雷系統在介電常數差異較小的分層媒質中的反演性能，本文利用相同的矢量網絡分析儀和天線在不改變頻率測量點和中頻帶寬等配置參數的條件下搭建了單站步進頻探地雷達系統。在實驗室條件下利用相同的石膏板和木板搭建了3層結構模型，其中第1層為空氣，第2層為石膏板，第3層為木板，并且用2.5 m×2.5 m的覆銅板充當分層媒質的底部邊界條件。同樣利用單站配置和準單站配置的探地雷達分別在3層結構上方不同高度處進行測量，并對測量波形進行反演。表4和表5分別展示了準單站配置和單站配置的雷達測量波形的反演結果。從結果中可以看出，對于兩個不同配置的探地雷達，反演得到的石膏板的介電常數都非常接近其真實值。對于木板的介電常數，由準單站配置的探地雷達得到的反演結果更接近真實值，且標準差更小。在石膏板和木板的厚度反演中，由準單站配置探地雷達系統得到的厚度反演誤差整體更小。表4和表5的結果表明，當分層媒質的介電常數差異較小時，準單站配置的探地雷達系統具有更好的反演性能。影響全波反演結果精度的一個主要因素就是信號的信噪比。為了理解準單站配置探地雷達系統的優勢，這里分析了兩個雷達系統獲得的信號的信噪比。在單站配置中，矢量網絡分析儀采用反射測量模式，其端口需要采用定向耦合器進行收發信號分離。由于定向耦合器的隔離度一般只有23 dB，因此在接收信號中有一部分是從發射端串擾過去的噪聲。經校準過的矢量網絡分析儀能獲得有效的方向性增益約為46 dB[13]，所以矢網在進行反射測量時其系統內部歸一化噪聲主要受系統的方向性增益影響。當矢網采用傳輸測量方式工作時，由于收發通道在物理上是隔離的，因此其歸一化噪聲主要受中頻帶寬影響。對于校準后的矢網，在其接收端口接上匹配負載可以實際測得其內部歸一化的噪聲水平。另外，當分層媒質的厚度和介電常數已知時，可以利用正演模型有效估計在不同的雷達配置下測量到的來自各分界面反射信號的歸一化功率。這里利用圖6(a)所示的3層結構模型來說明如何估計來自分界面的反射信號，由該3層媒質測得的反射信號可以看作是分別由分界面和產生的反射信號的疊加。

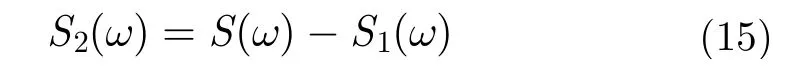
假定天線高度為525 mm，利用表1和表2中反演的石膏板()和木板()的介電常數，以及兩者的真實厚度(h2,h3)，依據式(15)可以準確計算來自石膏板和木板間的分界面的反射信號。圖7(a)和圖7(b)分別展示了兩種雷達配置下得到的歸一化反射信號和歸一化內部噪聲，以及對應的信噪比。可以看出，準單站配置探地雷達能獲得更高的信噪比，因此在反演中表現出更好的性能。

表4 準單站配置雷達3層結構反演結果Tab. 4 Inversion results of the three-layer structure with quasi-monostatic GPR

表5 單站配置雷達3層結構反演結果Tab. 5 Inversion results of the three-layer structure with monostatic GPR

圖6 分界面反射信號的計算模型Fig. 6 Models used to calculate the reflections on the interface

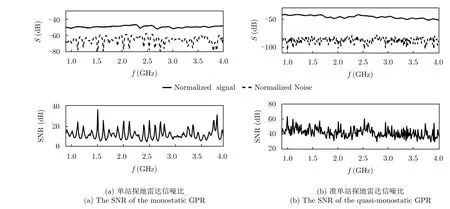
圖7 單站配置探地雷達和準單站配置探地雷達的信噪比對比Fig. 7 The comparison of the SNR between the monostatic and quasi-monostatic GPR

5 結束語

本文提出了一種用于準單站配置的步進頻探地雷達的正演模型。通過在已知厚度的石膏板和木板上方不同高度處進行測量，并對測得的雷達回波進行全波反演，證明了該正演模型具有很高的建模精度。通過利用石膏板和木板構建參數已知的3層模型，并分別構建單站配置探地雷達和準單站配置探地雷達進行參數反演，證明了當分界面上下介質介電常數差異較小時，準單站配置探地雷達因為其底噪更低能獲得更高的信噪比，因此反演性能更好。雖然本文中是利用VNA測試的結果驗證準單站配置探地雷達比單站配置探地雷達系統信噪比高，反演性能好，但是該結論同樣適用于其他形式構建的步進頻探地雷達系統。