基于無跡卡爾曼濾波的超空泡航行體最優控制研究

張成舉， 王聰， 曹偉， 王金強

(哈爾濱工業大學 航天學院, 黑龍江 哈爾濱 150001)

0 引言

當水下航行體運動速度到達50 m/s時，航行體頭部或整體會被空泡包裹，此時航行體稱為超空泡航行體。超空泡航行體高速運動時會出現兩種情況：一是航行體未被空泡全部包裹，航行體滑行力不為0；二是航行體被空泡全部包裹，航行體滑行力為0.海洋環境復雜多變，超空泡航行體受環境噪聲和測量噪聲的影響較大，因此超空泡航行體的運動控制具有極大的不確定性，所以超空泡航行體的運動控制是當今的研究熱點。

在超空泡航行體運動控制方面，已有許多學者開展了研究，例如：Dzieiski等[1]建立了縱平面內4狀態2自由度模型，對其基準問題開展了研究；Vanek等[2]考慮超空泡航行體運動過程中的空泡存在記憶效應，基于反饋線性化方法提出了雙閉環控制系統，證明了該控制系統的跟蹤控制有效性；Qiang等[3]改進了反步法，提出狀態反饋控制，對超空泡航行體的運動穩定性開展了研究；Nguyen等[4]考慮空泡形態變化會對超空泡航行體運動有重要影響，提出反饋控制，對超空泡航行體運動穩定性開展了研究；Lü等[5]基于保代價理論提出自適應滑模控制器，針對超空泡航行體存在非匹配不確定性問題開展了控制研究；Ruzzence等[6]運用最優方程獲取航行體的最優彈道，對航行體轉彎運動和下潛運動開展了研究；Mao等[7]對超空泡航行體提出基于反步法的自適應控制器，設計尾舵效率計算方法，利用李雅普諾夫方法證明了該方法的有效性；Zhao等[8]基于超空泡航行體空泡突變特性，對航行體變深控制進行了研究；白濤等[9]提出基于混合卡爾曼濾波的變深運動控制算法，針對超空泡航行體的測量噪聲干擾開展了研究，采用高斯白噪聲測量了噪聲，仿真結果表明該控制系統提高了系統的運動穩定性；龐愛平等[10]提出采用魯棒控制算法來保證超空泡航行體各個狀態變量在指定范圍內變化，通過仿真證明該系統具有較好的穩定性；呂瑞等[11]針對超空泡航行體提出基于增益自適應變結構控制算法，經過仿真驗證了該控制算法的有效性；王京華等[12]提出基于空泡記憶效應的超空泡航行體控制算法，通過仿真驗證了該控制算法的有效性；李洋等[13]提出針對超空泡航行體的反演控制算法，通過仿真驗證了該控制系統的穩定性。

根據以上文獻可知，采用濾波器同時降低環境干擾與測量干擾的研究較少。本文針對超空泡航行體受到環境噪聲和測量噪聲的影響，設計基于無跡卡爾曼濾波器(UKF)的最優控制器，通過仿真分析驗證了該控制器的有效性。

1 超空泡航行體動力學模型

以超空泡航行體縱平面內穩定問題為研究對象，通過對航行體建模受力進行分析，可知超空泡航行體主要受力如下：

1) 航行體所受重力G，重力方向指向地心。

2) 超空泡航行體發動機的推力T，推力作用方向與航行體縱軸重合。

3) 空化器轉動過程中為航行體提供的升力[1]：

(1)

式中：ρ為水的密度；Rn為空化器半徑；v為航行體航行速度；c0為空化器初始阻力系數；σ為航行體空化數；vy為航行體縱向速度；Lc為空化器頂端至航行體質心之間的距離；ωz為航行體俯仰角速度；δc為空化器轉角。

4) 超空泡航行體航行過程中，其空泡區域分為全沾濕區、半沾濕區和空泡包裹區。航行體空泡區域劃分如圖1所示，其中δf為航行體尾翼轉角。

圖1 超空泡航行體空泡區域示意圖Fig.1 Configuration of supercavitating vehicle’s cavitation

空化器轉動會使空泡軸線偏移，重力作用也會導致空泡上漂。對空泡形態預測利用較多的是Logvinovich[14]提出的空泡形態半理論和半經驗預測公式。本文采用此公式用于空泡形態預測，在文獻[11]提出的空泡狀態方程中，空泡截面為軸對稱橢圓，假設空泡在任意位置均為圓形，t時刻空泡半徑為

(2)

(3)

空泡受重力影響會導致空泡軸線發生偏移，在空化數σ<0.1且弗勞德數Fr較大的條件下，重力導致的空泡軸線偏移量為

(4)

式中：g為重力加速度；LRmax為空泡長度,LRmax=2Rn/(1.92/σ-3)；ζ=x/LRmax，x為空化器與空泡截面的距離。

空化器轉動對空泡形態影響較大，并且航行體俯仰運動對空泡產生極大的非線性干擾，基于獨立膨脹原理，空化器轉動導致空泡軸線偏移量為

hc=0.82(1+σ)(θ+δc)Rn(0.46-σ+ζ)，

(5)

式中：θ為航行體俯仰角。

當超空泡航行體部分處于沾濕狀態時，航行體尾部會與空泡之間發生接觸和碰撞，航行體產生滑行力。根據細長體理論，將滑行力簡化為工程中計算細長體浸入自由液面，采用如下考慮重力和空化器轉動的滑行力計算公式[2]：

(6)

式中：

(7)

(8)

R為航行體半徑，h′為沾濕深度，αp為航行體沾濕角，yc為空泡軸線與航行體軸線之間的縱向偏差，zc為空泡軸線與航行體軸線之間的側向偏差，ω為航行體旋轉角速度。

5) 尾舵包括俯仰舵和偏航舵，當尾翼處于沾濕狀態時，尾舵才能發揮作用；航行體運動過程中，尾翼與空泡之間的關系處于不確定狀態；假定航行體在縱平面內做小角度機動，此時可認為尾翼是一種楔形空化器，與空化器估算公式相同，則尾翼升力估算公式為

(9)

式中：η為尾翼升力與空化器升力的相似準數，這里取0.5；Lf為尾翼與航行體質心之間的距離。

建立動量定理和動量矩定理，可得超空泡航行體縱向運動模型矩陣：

(10)

(11)

I(t,τ)為尾舵沾濕率，

(12)

2 超空泡航行體最優控制器設計

采用精確線性化方法，利用非線性反饋變換實現輸入輸出的精確線性化[15]，首先將方程(10)式改寫為

(13)

式中：

(14)

(15)

(16)

(17)

(18)

y1、y2為輸出變量y的分量，n1、n2為充分光滑的標量函數。

對于此非線性多輸入多輸出(MIMO)系統，具有相對階向量(λ1,λ2)=(2,2)，總相對階[15]為λ1+λ2=4，這時不考慮內動態的穩定性，輸出變量與輸入的關系為

(19)

式中：Lχ、LMi(i=1,2)分別為向量χ(x)和M(x)的李導數。

通過反饋可得

(20)

將(20)式代入(19)式，可得

(21)

將(21)式精確線性化后，可得超空泡航行體狀態方程：

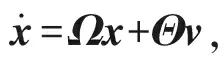
(22)

(23)

式中：ε(t)為線性二次型最優控制器；k1、k2、k3、k4為控制參數，其選擇應使兩個解耦子系統對應特征多項式的所有根均位于左半復平面；h1、h2、h3、h4為向量h(t)的分量，則可得誤差方程為

(24)

式中：

(25)

選取如下線性二次型性能指標離散泛函數：

(26)

式中：Q為對稱正定狀態加權矩陣；R為對稱正定控制加權矩陣。

當方程(26)式取得最小值時，可得線性二次型最優控制反饋控制器為

ε(t)=-R-1ΘTPh(t)，

(27)

式中：P為滿足Riccati方程(28)式的正定對稱矩陣，

HTP+PH-PΘR-1ΘTP+Q=0.

(28)

綜上所述，聯立方程(20)式、方程(23)式和方程(27)式，可得基于精確線性化后的最優控制器表達式為

(29)

3 帶有環境噪聲和測量噪聲的最優控制算法仿真分析

令：超空泡航行體初始縱向速度vy=-4 m/s，俯仰角θ=3°，航行深度y=-4 m,俯仰角速度ωz=7°/s；正弦跟蹤方程為y(t)=-sint-5；航行體航行速度v=75 m/s，質量m=22 kg，重力加速度g=9.81 m/s2,空化器半徑Rn=0.019 1 m，航行體柱段半徑R=0.050 8 m，航行體總長L=1.8 m，空化數σ=0.03，水的密度ρ=998 kg/m3,Lc=17L/28,Lf=11L/28.

采用經輸入輸出精確線性化后的最優控制器對超空泡航行體進行位置跟蹤控制；環境噪聲和測量噪聲幅值均為0.02 m/s的高斯白噪聲[9]。考慮到較小的控制誤差，經過多次仿真實驗，為保證控制精度，選取控制參數k1=k2=k3=k4=20，

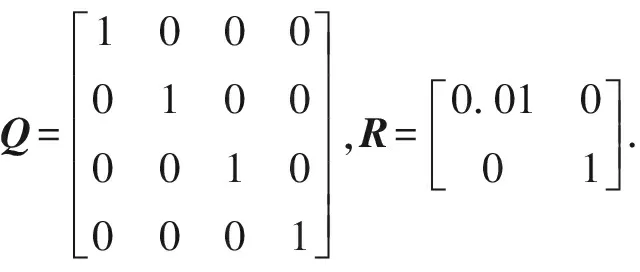
(30)

將Q和R值代入方程(29)式，滿足P為正定矩陣。采用以上參數進行仿真，驗證算法的有效性，仿真時間為20 s，仿真結果如圖2～圖8所示。

圖2 航行體深度變化(無濾波器)Fig.2 Change of depth (without filter)

圖3 航行體縱向速度變化(無濾波器)Fig.3 Change of vertical speed (without filter)

由圖2～圖8可知，超空泡航行體在環境噪聲和測量噪聲干擾下出現持續無規則振蕩。由于環境噪聲和測量噪聲的干擾，航行體滑行力呈現無規則振蕩，給航行體運動控制帶來了困難。

圖4 航行體俯仰角速度變化(無濾波器)Fig.4 Change of pitch angular velocity (without filter)

圖5 航行體俯仰角變化(無濾波器)Fig.5 Change of pitch angle (without filter)

圖6 航行體滑行力變化(無濾波器)Fig.6 Change of sliding force (without filter)

根據上述對超空泡航行體在環境噪聲和測量噪聲干擾下的運動狀態分析可知，超空泡航行體的運動是極其不穩定的。因此，在超空泡運動控制中有必要加入卡爾曼濾波器，使航行體減少干擾噪聲的影響。

圖7 航行體空化器轉角變化(無濾波器)Fig.7 Change of cavitor angle (without filter)

圖8 航行體尾翼轉角變化(無濾波器)Fig.8 Change of tail angle (without filter)

4 基于UKF的最優控制算法

本文針對以上超空泡航行體的運動不穩定性，提出基于UKF的最優控制算法，解決超空泡航行體的噪聲干擾問題。UKF采用卡爾曼線性濾波框架，對于一步預測方程，使用如下無跡變換處理均值和協方差的非線性傳遞問題：

(31)

式中：x(k+1)為k+1時刻的系統狀態；f(x(k),W(k))為非線性狀態方程函數，W(k)為環境噪聲；y(k)為觀測變量；h(x(k),V(k))為非線性觀測方程函數，V(k)為測量噪聲；W(t)為協方差S1的連續時間高斯白噪聲；V(t)為協方差S2的連續時間高斯白噪聲。

具體處理步驟如下：

1) 獲取超空泡航行體的一組采樣點，設置如下初值：

x(i)(k|k)=
[(k|k)(k|k)+T(k|k)-T]，

(32)

式中：x(i)(k|k)為k時刻超空泡航行體狀態值，i為第i個采樣點，i=1,2,…,2n，n為狀態維數；(k|k)為k時刻狀態估計值；為半正定矩陣，D(k|k)為狀態x(k|k)的方差，λ為縮放比例參數，λ=α2(n+a)-n，用于減小總的預測誤差；α為控制采樣點分布狀態的參數，用于調整Sigma點與均值點的距離。

2) 計算2n個Sigma點集的一步預測：

x(i)(k+1|k)=f[k,x(i)(k|k)]，

(33)

式中：x(i)(k+1|k)為超空泡航行體k+1時刻的預測狀態；f[k,x(i)(k|k)]為k時刻的非線性狀態方程。

3) 預測超空泡航行體的系統狀態量與方差：

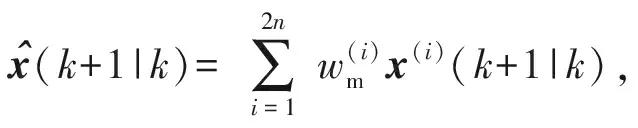
(34)

式中：wm為采樣點均值的權值；wc為采樣點協方差的權值。

采樣點均值的權值和協方差的權值計算公式如下：

(35)

4) 根據一步預測值，再次運用無跡變換產生新的Sigma點集：

(36)

5) 量測更新方程，得到Sigma點集的觀測預測值，通過加權求和得到超空泡航行體系統預測的均值、狀態量和觀測量之間的協方差、新息序列的協方差分別為

(37)

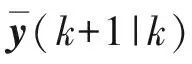
6) 計算卡爾曼增益矩陣：

(38)

7) 計算系統的狀態更新和協方差更新：

k(k+1|k+1)=k(k+1|k)+Kk(yk-k)，
D(k+1|k+1)=

(39)

5 基于UKF的最優控制仿真分析

令：超空泡航行體初始縱向速度vy=-4 m/s，俯仰角θ=3°，航行深度y=-4 m,俯仰角速度ωz=7°/s；α通常選取一個較小的正實數(一般10-4≤α≤1)，α=0.01；a為待選參數，需要保證矩陣(n+λ)D(k|k)為半正定矩陣；κ=0；β用于合并方程中高階項的動差，調節β可改善方差的精度，對于高斯分布，β=2時最優。選取的控制器參數k1=k2=k3=k4=20，Q和R與第3節相同，對選取的深度信號y(t)=-sint-5進行深度跟蹤，仿真時間20 s時得到仿真結果如圖9～圖15所示。

圖9 航行體深度變化(含濾波器)Fig.9 Change of depth (filter)

由圖9～圖14可知，通過運用UKF對噪聲干擾處理，超空泡航行體處于穩定運動狀態。

由圖9可知，經過UKF處理后的跟蹤信號與理想信號相差較小，誤差能夠控制在0.1 m內，而且未出現跟蹤延遲現象。

由圖10可知，超空泡航行體俯仰角速度急劇反向轉變，在4 s時趨于穩定狀態，經過濾波器處理后俯仰角速度跟蹤誤差控制較小。

圖10 航行體俯仰角速度變化(含濾波器)Fig.10 Change of pitch angular velocity (filter)

圖11 航行體縱向速度變化(含濾波器)Fig.11 Change of vertical speed (filter)

由圖11可知，超空泡航行體縱向速度變化穩定，跟蹤誤差在0.1 m/s范圍內。

由圖12可知，超空泡航行體俯仰角逐漸較小，變化率逐漸減小，在4 s時航行體俯仰角趨于穩定，經過UKF處理后的俯仰角跟蹤誤差控制較小。

圖12 航行體俯仰角變化(含濾波器)Fig.12 Change of pitch angle (filter)

圖13 航行體滑行力變化(含濾波器)Fig.13 Change of sliding force (filter)

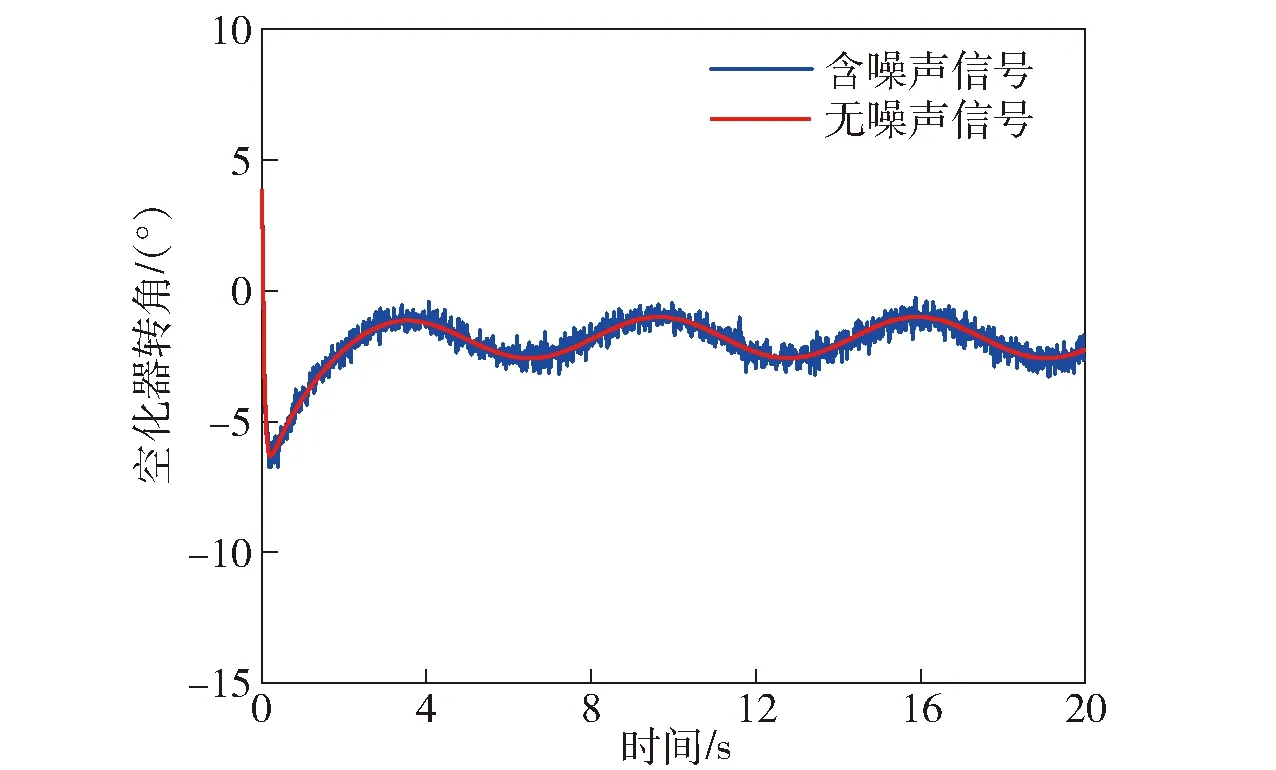
圖14 航行體空化器轉角變化(含濾波器)Fig.14 Change of cavitor angle (filter)

由圖13可知，超空泡航行體起始狀態時航行體包裹面積較大，滑行力較小。開始運動后，滑行力呈現先增大、后減小現象，之后航行體滑行力減小為0，此時航行體除空化器外，均為空泡包裹，經過UKF處理后的滑行力信號與理想狀態相差無幾。在航行體滑行力穩定之前，誤差控制在0.1 kN范圍內，但是從起始狀態到穩定狀態，經過UKF處理后的滑行力信號仍然比理想信號延遲。

由圖14和圖15可知，航行體空化器轉角與尾翼轉角偏轉范圍較小，與理想信號較為接近。

圖15 航行體尾翼轉角變化(含濾波器)Fig.15 Change of tail angle (filter)

綜合以上分析可知，通過運用UKF對噪聲進行有效處理，可使超空泡航行體達到穩定運動狀態。

6 結論

本文以最優控制為基礎，提出超空泡航行體UKF最優控制策略，通過仿真實驗得到如下結論：

1)在環境噪聲和測量噪聲干擾下，超空泡航行體運動極其不穩定。

2)在UKF作用下，航行體運動狀態改變明顯，達到穩定狀態所需時間減小。

3)將UKF引入狀態觀測器的設計，可以獲得環境噪聲和測量噪聲干擾下的最優狀態估計量，從而實現航行體的高精度控制，減少輸入輸出線性化后帶來的誤差。