多層混凝土介質內爆炸相似性分析

謝述春， 姜春蘭， 王在成， 盧廣照

(北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

0 引言

反堅固目標彈藥對機場跑道、港口及高速公路等目標的內爆炸毀傷效應及威力評估，是兵器領域的研究熱點。上述目標通常是由面層高強度混凝土、貧混凝土基層及壓實土層組成的多層混凝土介質。在目前彈藥設計及威力評估過程中，試驗研究仍是不可或缺的重要方法。以相似理論為基礎的縮比模型試驗能節約成本，縮短試驗周期，成為研究爆炸毀傷效應的一種重要手段。因此，分析多層混凝土介質內爆炸相似律，建立原型與縮比模型的相似準則，使模型試驗能夠預測原型試驗的毀傷效果，具有重要現實意義。

關于混凝土或混凝土- 土介質在爆炸載荷作用下的成坑相似律，部分學者通過相似理論建立了相似準則。Westine[1]分析了混凝土- 土復合介質內爆炸毀傷效應的關鍵影響因素，基于量綱分析法建立了相似模型。Chabai[2]在深埋裝藥的爆炸成坑效應中考慮了重力影響，得到4次方根比例定律，即r∝Q1/4(Q為炸藥釋放的總能量，r為相似比)。楊振聲[3]和談慶明[4]分析了工程爆破模型律，研究表明當介質拋擲高度y1與最小抵抗線W為同一量級時，即最小抵抗線超過25 m時需考慮重力影響。Wang等[5]分析了雙層混凝土介質中的爆炸相似律，得到考慮重力時模型律的兩種方法：慣性加速度法(采用離心機實現)和等效材料法(材料強度進行縮比)。岳松林等[6]推導了巖石內爆炸成坑相似律，闡述了地下深埋爆炸效應的模型試驗方法，隨后徐小輝等[7]給出了模型試驗等效材料的相似條件。楊亞東等[8]和Yao等[9]分析了縮比系數對密閉空間內爆炸相似律的影響。Xie等[10]基于相似理論建立了土壤爆破彈坑參數的無量綱經驗公式。荊松吉等[11]采用有限元分析軟件LS-DYNA分析了多層混凝土介質的爆炸相似律，分析表明多層混凝土介質中存在相似律，但縮尺比例過大時，會通過面效應影響原型與縮比模型的相似性。

上述文獻主要是基于相似理論分析混凝土- 土復合介質結構內爆炸相似律，對多層混凝土介質內爆炸相似律的研究較少。基于量綱分析法和數值模擬的混凝土內爆炸相似律分析都是將混凝土看成均質材料，需要通過考慮骨料的內爆炸試驗對相似律進行驗證。此外，由于含鋁炸藥具有高爆熱、高爆容和釋能時間長的優點，廣泛應用于航空武器彈藥，而含鋁炸藥中鋁粉與爆轟產物的二次反應表現出非理想性，在多層混凝土介質內爆炸毀傷是否滿足相似律，需要相關研究驗證。

本文利用量綱理論導出多層混凝土介質內爆炸毀傷相似律，建立內爆炸相似理論模型。在理論分析基礎上，利用LS-DYNA軟件進行了不同裝藥深度和縮尺比例下原型和縮比模型的內爆炸數值仿真，并采用梯恩梯(TNT)和含鋁炸藥進行原型和縮尺比例為1/2的縮比模型內爆炸相似性驗證試驗。通過仿真和試驗分析了裝藥深度及鋁粉的二次反應釋能對毀傷效應參量、介質拋擲速度和位移相似性的影響，揭示了縮尺比例對內爆炸毀傷效應參量的影響，論證了模型試驗的可行性。所得結論可為多層混凝土介質內爆炸縮比模型試驗設計提供參考依據。

1 多層混凝土介質內爆炸相似模型

1.1 毀傷效應參量及影響因素

裝藥在多層混凝土介質內爆炸毀傷效應參量主要有：實際彈坑深度H(實際彈坑底部到地表的距離)；彈坑半徑Rc(混凝土道面上彈坑的平均半徑)；有效毀傷半徑Reff(混凝土道面上環向裂紋的平均半徑)；最大空腔半徑Rmax(在成坑模式中，Rmax一般等于Rc)；鼓包隆起過程中的鼓包位移y和鼓包速度v. 此外，還引入1個參量MODE來描述毀傷模式(成坑模式、隆起模式或隱坑模式)。

上述毀傷參量的主要影響因素來自裝藥、混凝土、土壤的材料性質及幾何尺寸等，包括：

1)裝藥：裝藥量w，裝藥密度ρe，裝藥爆熱Qe和爆轟產物膨脹指數γ；

2)多層混凝土介質靶：面層混凝土參數包括面層厚度hf、面層長度、寬度lf、反映慣性效應的材料密度ρf、反應強度效應的材料極限抗壓強度σf；碎石層參數包括碎石層厚度hm、介質材料密度ρm、極限抗壓強度σm；壓實土壤層包括介質密度ρs、聲速cs. 聲速cs和密度ρs反映材料強度效應的影響。忽略多層混凝土介質材料的應變率效應，認為其他強度參數與抗壓強度呈正比；

3)交會參數：裝藥深度h和裝藥傾斜角度α.

1.2 內爆炸毀傷量綱分析

在進行量綱分析前作如下假設[12]：1)不考慮介質應變率的影響，忽略介質的黏性和熱傳導；2)混凝土為各向同性的脆性材料；3)忽略爆轟產物初始壓力的泄露；4)由于炸藥裝藥深度較小，忽略重力影響；5)炸藥瞬時爆轟。表1和表2分別列出了7個毀傷效應參量和15個影響因素及其量綱(以M、L和T為基本量綱)。

表2 影響因素及其量綱

選取w、Qe和h為基本量，可將7個毀傷效應參量寫成無量綱形式：

(1)

(2)

當縮比試驗和原型試驗中采用的炸藥類型、密度及靶板材料、強度和密度相同，以及縮尺比例為λ時，求解(2)式可得相似模型如下：

(3)

由πip=πim可得原型和縮比模型的毀傷效應參量關系，如表3所示。

表3 原型和縮比模型毀傷效應參量關系

根據表3中原型和縮比模型體系內的鼓包位移及速度關系，可知時間滿足tm/tp=λ. 下面通過數值模擬檢驗相似模型的正確性，并分析裝藥深度和縮尺比例對相似性的影響。

2 內爆相似性數值模擬

2.1 計算模型及材料參數

多層混凝土介質由40 cm厚混凝土、40 cm厚碎石層和120 cm厚壓實土層組成，如圖1所示。其中混凝土面層由邊長為5 m的正方形中心靶及寬度為1.5 m的邊界靶組成，中心靶和邊界靶存在1 cm的間隙。裝藥為TNT炸藥，位于靶板中心位置，并用壓實土填充炮孔。考慮到結構的對稱性，建立1/4模型，數值模擬采用多物質Euler材料與Lagrange結構相耦合的算法，其中面層混凝土采用單點積分Lagrange六面體網格，其余均采用Euler六面體網格，原型網格尺寸為3 cm，縮比模型網格尺寸根據縮尺比例縮比，即縮尺比例為1/2的縮比模型網格尺寸為1.5 cm.

圖1 1/4計算模型Fig.1 A 1/4 simulation model

TNT炸藥采用High_Explosive_Burn材料模型及JWL狀態方程描述。

(4)

表4 TNT炸藥材料參數

圖2 原型和縮比模型的毀傷效果Fig.2 Damage effect diagrams of prototype and scale model

混凝土采用TCK模型，其主要特點是把動態脆性破裂過程看作拉伸損傷的累積，材料的壓縮響應看作理想彈塑性。通過用戶自定義模型材料接口將TCK模型嵌入LS-DYNA中，混凝土材料模型參數如表5所示。表5中：Ef為楊氏模量，Yf為屈服強度，ν為泊松比，kic為材料斷裂韌性，k為材料常數，Fs為拉伸失效應變，Fd為壓縮失效應變。

表5 混凝土材料參數

碎石層采用流體彈塑性模型和Gruneisen狀態方程，其中ρm=2.2 g/cm3，Ym=8 MPa. 壓實土層采用帶失效的土壤與泡沫材料模型，具體參數見文獻[13]。

2.2 裝藥深度對相似性影響分析

本節建立原型(縮尺比例為1)和縮尺比例為1/2的縮比模型內爆炸毀傷計算模型，分析不同裝藥深度下原型與縮比模型毀傷效應參量(彈坑口部半徑、有效毀傷半徑、最大爆腔半徑和彈坑深度)的相似性。其中原型裝藥量為3 kg TNT，裝藥深度分別為40 cm、60 cm和90 cm，靶板尺寸如2.1節所示。縮比模型的長度尺寸減小一半，即面層和碎石層為20 cm，壓實土層為60 cm，裝藥量為0.375 kg，裝藥深度分別為20 cm、30 cm和45 cm，所有材料模型及參數保持不變。

2.2.1 毀傷形態對比

3種裝藥深度下的原型和縮比模型毀傷效果如圖2所示，其中原型為40 ms時的毀傷效果，縮比模型為20 ms時的毀傷效果，此時毀傷形態基本形成。由圖2對比可知：不同裝藥深度下原型和縮比模型的毀傷特性較為一致，原型和縮比模型的面層混凝土均出現了破碎和裂紋，碎石層和壓實土層形成的爆腔形態相同，由于土壤強度較低，壓實土層的空腔較碎石層大。在裝藥深度H分別為40、60 cm時，原型和縮比模型的面層出現徑向裂紋，裂紋的走向和條數較為一致。由此可以看出，不同裝藥深度下原型和縮比模型的毀傷形態具有相似性。

2.2.2 毀傷過程對比

以原型裝藥深度60 cm為例，對比原型和縮比模型毀傷過程中介質運動的相似性。原型選取混凝土面層表面距圓心分別為50 cm、100 cm和150 cm的3個節點，縮比模型距圓心為25 cm、50 cm和75 cm 3個節點，分別對比不同位置處的豎直方向節點速度和位移。圖3和圖4分別為節點位移和節點速度時程曲線，由于位移和速度均與時間有關，為了方便比較相似性，將縮比模型的位移和速度曲線化為原型時間體系下的時程曲線。從圖3中可以看出，原型和縮比模型相似位置處的節點位移較為一致，不同位置處的節點位移滿足相似模型中的yp/ym=2的相似關系。從圖4中可以看出，不同位置處原型和縮比模型的節點速度時程曲線趨勢相同，只是距離炸藥較近的節點在末端速度差別較大，原因是距離炸藥較近時，由于沖擊波作用，會產生層裂和拋擲現象，造成節點速度有所差別，但兩個體系下的速度近似滿足vp/vm=1的相似關系。因此原型和縮比模型的毀傷過程滿足相似性。

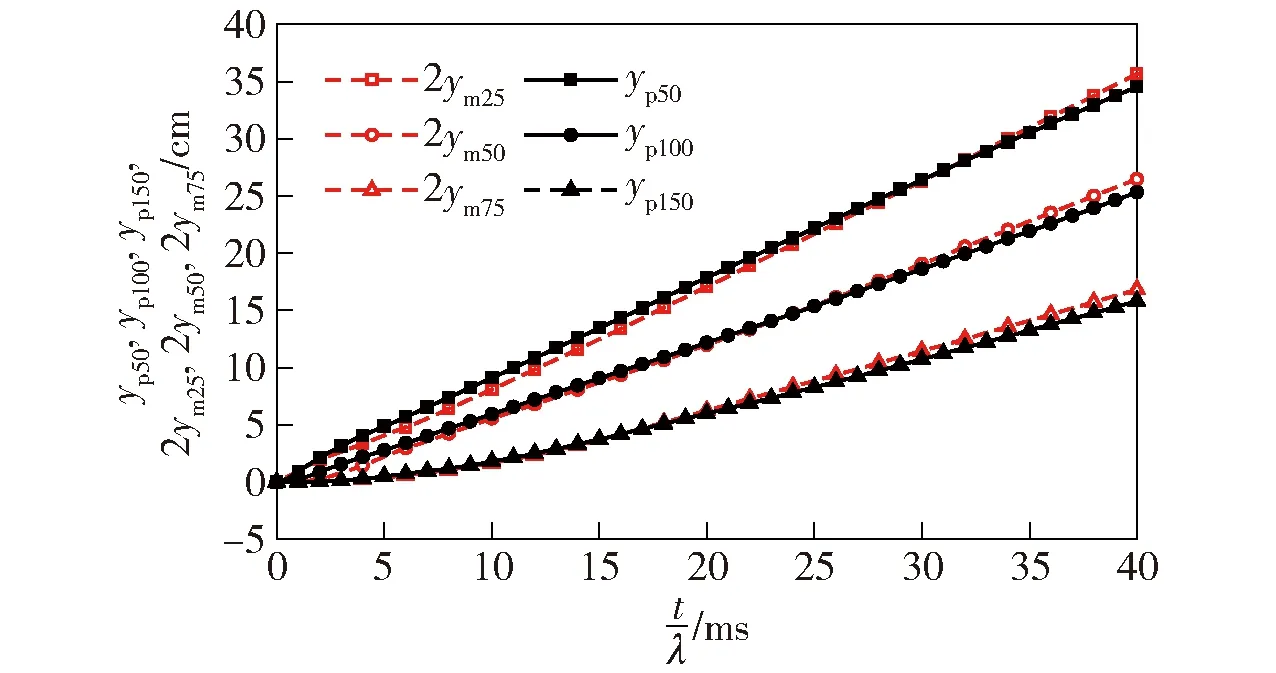
圖3 節點位移時程曲線Fig.3 Nodal displacement vs. time

圖4 節點速度時程曲線Fig.4 Nodal velocity vs. time

2.2.3 毀傷效應參量的對比

多層混凝土介質的毀傷包括炸坑、爆腔、裂紋及隆起，由于毀傷效果的復雜性，難以精確判斷毀傷半徑。本文的有效毀傷半徑是指面層混凝土嚴重毀壞區域(包括炸坑和環向裂紋內部的隆起，沒有考慮徑向裂紋的影響)半徑，不同裝藥深度下原型和縮比模型的彈坑口部半徑Rc、有效毀傷半徑Reff、最大爆腔半徑Rmax和彈坑深度H(兩次測量平均值)如表6所示，原型裝藥深度為90 cm時，沒有形成漏斗坑，由于計算模型的壓實土層厚度不夠，無法測量彈坑深度。從表6中可以看出，原型和縮比模型的彈坑口部半徑、有效毀傷半徑和彈坑深度的相似比差別不大，均在1∶0.48到1∶0.52之間，而不同炸點深度下的爆腔相似比差別較大，主要原因是網格數量較少引起的介質流動界面的誤差。由此可見原型和縮比模型的毀傷效應參量滿足2∶1的幾何相似性。

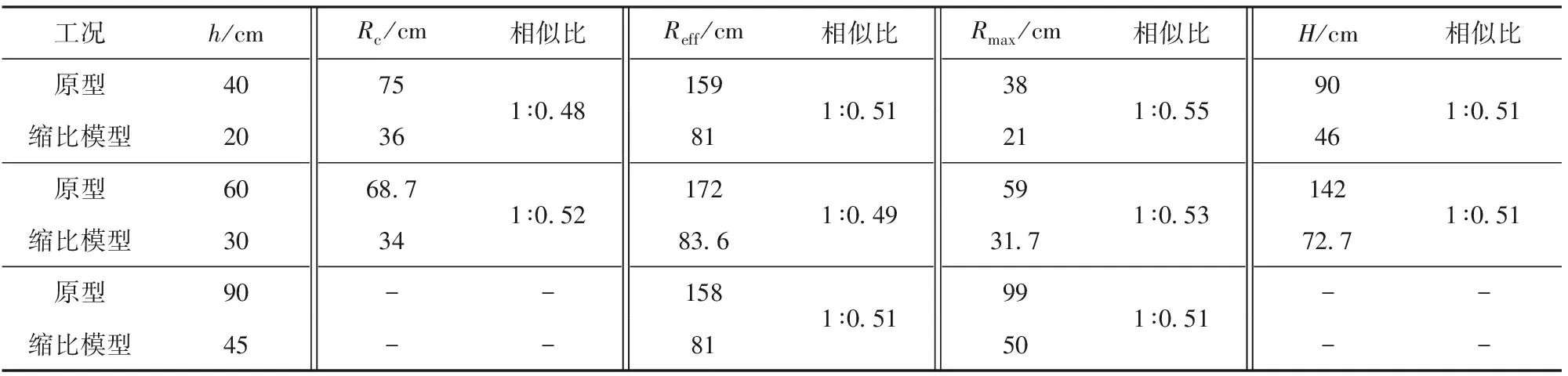
表6 不同裝藥深度下的毀傷效應參量

2.3 縮尺比例對相似性影響分析

分別進行縮尺比例為1、1/2、1/4和1/6的縮比模型內爆炸毀傷仿真，分析不同縮尺比例下的內爆炸毀傷效應參量是否滿足相似規律。裝藥量分別為3 kg、375 g、46.88 g和13.89 g(原型的1/λ3)，裝藥深度分別為60 cm、30 cm、15 cm和10 cm，靶板尺寸按縮尺比例縮小，材料模型和參數不變。其中縮尺比例λ=1和λ=1/2的毀傷效果如圖2(b)和圖2(e)所示，縮尺比例λ=1/4和λ=1/6的毀傷效果如圖5所示，不同縮尺比例下的毀傷效應參量如表7所示。

圖6為不同縮尺比例下的毀傷效應參量歸一化(除以縮尺比例)后與原型毀傷參量相似性對比。

從圖5中可以看出，原型和縮尺比例為1/2的模型裂紋擴展及毀傷區形態相似，進一步增大縮尺比例時，毀傷區形態差異逐漸增大，表面無徑向擴展裂紋。從表7和圖6可以看出，原型與不同縮尺比例的縮比模型歸一化后彈坑口部半徑比為1∶0.98∶0.96∶0.72，有效毀傷半徑比為1∶0.98∶0.96∶1.08，最大爆腔半徑比為1∶1.06∶1.12∶1.2，彈坑深度比為1∶1.02∶1.01∶1.05. 隨著縮尺比例的增加，毀傷效應參量與原型的偏差逐漸增大，相似性呈減小趨勢，λ=1/6時的縮比模型歸一化后與原型的毀傷參量相對誤差最大為28%. 這是因為：1)縮尺比例逐漸變小時，毀傷效應參量的取值偏差逐漸增大；2)多層混凝土介質內爆炸毀傷存在層裂、崩落和層間相互作用等面效應[6]，從能量角度來看，當縮尺比例逐漸減小時，用于面效應的能量占總能量的比例逐漸增加，對相似性的破壞越嚴重；3)原型和縮比模型的靶板材料和強度相同，導致斷裂韌性相同，不符合相似律，因此縮比模型對靶板的斷裂抗力比原型大。由此可見，多層混凝土介質內爆炸縮比模型試驗的縮尺比例不宜過小，一般不能小于1/4.

圖5 毀傷效果圖Fig.5 Damage effect

表7 不同縮尺比例下的毀傷參量

Tab.7 Damage parameters at different scale proportions

λRc/cmReff/cmRmax/cmH/cm168.7172.059.0142.01/234.083.631.772.71/416.841.016.836.01/68.131.011.824.8

圖6 縮尺比例對毀傷效應參量的影響Fig.6 Influence of scale ratio on damage parameters

3 內爆相似性試驗驗證

由于數值模擬中將混凝土視為均質材料，沒有考慮混凝土中骨料對相似律的影響，仿真也無法驗證含鋁炸藥在多層混凝土介質內爆炸相似性，因此構建原型和縮尺比例為1/2的縮比模型，分別采用TNT和海薩爾(RDX/Al/binder)炸藥進行內爆炸相似性驗證試驗。

3.1 試驗概況

原型靶為邊長5 m的正方形，由40 cm厚混凝土層、40 cm厚碎石層和半無限厚壓實土壤層組成，縮比模型尺寸根據原型按縮尺比例λ=1/2進行縮比，如圖7所示，各塊靶標間由1 cm厚木板隔開，靶標中間預留裝藥孔。裝藥分別為TNT和海薩爾，原型裝藥量為3 kg，其中TNT裝藥深度為53 cm，海薩爾裝藥深度為51 cm. 縮比模型裝藥量為375 g，裝藥深度按縮尺比例縮比，炸藥裝填及起爆方式如圖8所示。

圖7 試驗靶標Fig.7 Test target

圖8 裝藥裝填方式Fig.8 Filling method of explosive

3.2 鼓包隆起過程相似性分析

以海薩爾炸藥爆炸毀傷原型和縮比模型為例，兩個體系相似時間處的鼓包隆起過程如圖9所示。從圖9中可以看出，由于鋁粉燃燒，在縮比模型中可以看到火光從炮孔中噴出，原型和縮比模型的鼓包隆起過程相似，均先產生徑向裂紋，后產生環向裂紋，在爆生氣體作用下，徑向裂紋和環向裂紋逐漸擴展變寬，最后形成梯形混凝土碎塊。

圖9 鼓包隆起過程(海薩爾炸藥)Fig.9 Swelling heights at different times (Hexal explosives)

圖10 鼓包隆起高度- 時間曲線Fig.10 Swelling heights at different times

通過分析高速攝影機獲得的各種工況鼓包運動過程，得到TNT和海薩爾炸藥爆炸毀傷縮比模型和原型在不同時刻處的鼓包隆起高度和速度，分別如圖10和圖11所示，其中原型λ=1，縮比模型λ=1/2.

圖11 鼓包隆起平均速度- 時間曲線Fig.11 Average velocity-time curves of bulge

從圖10中可以看出，TNT和海薩爾炸藥在相似時間處的鼓包隆起高度近似滿足Hp/Hm=2，其中TNT的縮比模型隆起高度除以縮尺比例后與原型的最大誤差為8%，海薩爾炸藥的最大誤差為6%. 從圖11中可以看出，原型和模型體系中的速度近似滿足vp/vm=1，其中TNT體系速度偏差較大的原因是因為縮比模型中有兩邊界約束較弱，應力波達到邊界后沒有反射，造成能量外泄，導致縮比模型的鼓包平均速度與原型相比較小。由此可以看出，在邊界約束相同時，原型與縮比模型的隆起過程符合相似規律。

3.3 毀傷效應參量相似性分析

TNT和海薩爾炸藥的爆炸毀傷效果如圖12所示。從圖12中可以看出，由于TNT爆炸毀傷試驗的縮比模型靶標有兩邊界約束較弱，造成部分區域隆起高度較大，但縮比模型和原型的裂紋條數均為8條，擴展方向也大致相同，只是縮比模型由于邊界效應導致裂紋寬度較大。海薩爾炸藥的原型和縮比模型毀傷效果大致相同，均為成坑模式，徑向擴展裂紋均為9條，裂紋擴展方向也相同。由此可以看出，邊界約束相同時，原型和縮比模型的毀傷模式及裂紋擴展形態吻合較好。

圖12 爆炸毀傷效果圖Fig.12 Damage effect diagram of explosion

TNT和海薩爾炸藥毀傷原型和縮比模型后的毀傷效應參量如表8所示。

表8 毀傷效應參量的對比

注：Dc為彈坑口部直徑，Deff為環向裂紋直徑。

通過對比可知，TNT炸藥毀傷的原型與縮比模型彈坑口部直徑比約為1∶0.35，環形裂紋直徑比為1∶0.47，最大爆腔半徑比為1∶0.52，實際彈坑深度比為1∶0.47. 除彈坑口部直徑外，縮比模型的毀傷參量(環向裂紋直徑、最大爆腔半徑和實際彈坑深度)除以縮尺比例后與原型的誤差均在6%以內。彈坑口部直徑偏差較大是因為靶板邊界效應的影響，縮比模型在沖擊波和爆轟氣體的作用下，部分靶塊隆起高度較大，導致面層混凝土崩落較少，彈坑口部直徑較小，使彈坑口部的相似比偏差較大。

海薩爾炸藥毀傷的原型與縮比模型毀傷模式相同，且原型和縮比模型邊界約束相同，其彈坑口部直徑比為1∶0.52，均無環向裂紋，最大爆腔半徑比為1∶0.70，實際彈坑深度比為1∶0.54. 除最大爆腔半徑外，縮比模型的毀傷參量(彈坑口部直徑和實際彈坑深度)除以縮尺比例后與原型的誤差均在8%以內，最大爆腔半徑相似比的誤差較大的原因可能是因為混凝土層和碎石層的強度相差較大，在爆生氣體的作用下，兩層介質間出現了分層，使試驗測量的爆腔半徑包含層間間隙的長度，導致縮比模型的最大爆腔半徑偏大。另外，由于靶板養護的差別，試驗中材料的力學性能也不可能完全相同，會存在一定離散，造成試驗結果存在一定誤差。因此在邊界約束相同條件下，兩種炸藥的原型和縮比模型毀傷效應參量滿足幾何相似性。

4 結論

本文通過建立多層混凝土介質內爆炸毀傷效應相似模型，并對內爆炸毀傷效應參量和毀傷形態的相似性進行數值模擬和試驗研究。得出結論如下：

1)適當的縮尺比例下，不同裝藥深度下原型和縮比模型的毀傷形態相同，毀傷效應參量(彈坑口部半徑、有效毀傷半徑、最大爆腔半徑和彈坑深度)滿足幾何相似性，原型和縮比模型的鼓包隆起高度和速度服從相似規律。

2)在邊界約束條件相同時，含鋁炸藥在原型和縮比模型(λ=1/2)內爆炸毀傷破壞現象相同，毀傷效應參量符合相似性，除最大爆腔半徑外，毀傷特征參量歸一化后與原型的誤差均在8%以內。

3)隨著縮尺比例的減小，縮比模型的毀傷形態與原型差異增大，毀傷效應參量與原型的偏離程度也逐漸增大，相似程度呈下降趨勢。工程上可采用縮尺比例不小于1/4的縮比模型來預測原型的內爆炸毀傷效應。