基于互協方差的L型嵌套陣列二維波達方向估計

高曉峰， 栗蘋， 李國林， 郝新紅， 賈瑞麗

(北京理工大學 機電動態控制重點實驗室， 北京 100081)

0 引言

波達方向(DOA)估計作為陣列信號處理技術中的重要領域，在無線通信、水下探測[1-2]、聲探測[3-4]、雷達探測[5]等領域具有廣泛應用。近年來，不同陣列結構的二維DOA估計研究越來越受到關注，如雙平行陣[6-7]、圓陣[8-9]、十字陣[10-11]、矩形陣[12-13]、L型陣[14-19]等。與其他陣列相比，L型陣因其具有更好的估計性能和更低的克拉美羅界[20]成為二維DOA估計的研究熱點。文獻[14]提出將傳播算子方法應用到L型陣列上進行二維DOA估計,避免了對協方差矩陣進行奇異值分解和特征值分解。文獻[15]提出利用L型陣列互相關矩陣的二維DOA估計方法，利用互相關矩陣消除了噪聲影響。文獻[16]提出一種基于L型陣列的互相關矩陣聯合奇異值分解的DOA估計方法，利用互相關矩陣實現角度自動匹配。文獻[17]提出一種基于L型陣列的二維盲DOA估計方法，將不同方向的陣列分解出滿足子空間旋轉不變性的子陣，在不同方向分別利用旋轉不變子空間技術(ESPRIT)算法進行DOA估計。文獻[18]提出利用L型陣列不同方向的陣元信號進行互協方差運算，利用互協方差矩陣構建兩個互為共軛的矩陣，對矩陣進行奇異值分解，實現二維DOA估計。文獻[19]提出一種基于L型陣列的低復雜度二維DOA估計方法，將互相關矩陣劃分為不同子矩陣，利用滿足旋轉不變性的傳播算子方法進行二維DOA估計。上述基于L型陣列的DOA估計算法大多為針對均勻陣列的子空間類算法，需要對協方差矩陣采用特征值或奇異值分解等信號處理方法劃分信號子空間和噪聲子空間，估計性能受信噪比的影響較大，在低信噪比環境下算法估計精度較差。均勻陣列的角度分辨率與陣元孔徑呈反比，可估計的空間信源數小于陣元數，因此在陣元數有限時均勻陣列受限于陣列孔徑和陣元個數，難以獲得較高的DOA估計精度，可估計的空間信源數較少。

與均勻陣相比，稀疏陣在陣元數相同情況下具有更大的孔徑、更小的陣元間互耦效應，因此獲得了學術界的廣泛關注，如最小冗余陣列[21]、互質陣列[22]和嵌套陣列[23]等。與其他稀疏陣相比，嵌套陣列易于構造，產生的虛擬陣列具有固定的解析表達式，利用接收信號的協方差矩陣由O(M)個陣元(M為陣元數)能夠獲得O(M2)的自由度，具有較好的DOA估計效果。

本文針對上述L型均勻陣列在二維DOA估計中的問題，提出一種基于互協方差的L型嵌套陣列二維DOA估計算法。采用由兩個相互正交的2階嵌套陣構成的L型陣列，利用不同子陣信號進行互協方差運算，得到互協方差矩陣，并基于不同子陣噪聲不相關、互協方差矩陣消除了噪聲的影響；對互協方差矩陣進行列向量化、產生無冗余陣元的虛擬陣列，利用虛擬陣列及其共軛矩陣構建滿秩的Toeplitz矩陣作為等效協方差矩陣；利用等效協方差矩陣之間的子空間旋轉不變性，通過ESPRIT算法實現了目標的方位估計；基于虛擬陣列等效信源向量的唯一性，通過估計虛擬陣列的等效信源向量實現空間信源的角度匹配。與L型均勻陣列相比，本文算法通過互協方差矩陣產生了更多的虛擬陣元，獲得了更高的角度自由度，在低信噪比環境下具有更高的估計性能，但也不可避免地增加了計算復雜度，在實際應用中針對具體應用背景需要加以考慮。

符號說明：(·)T、(·)H、(·)-1分別表示矩陣轉置、共軛轉置、求逆；diag(·)表示對角矩陣；∏N表示N×N階的反對角單位矩陣；⊙表示Khatri-Rao積；vec(·)表示矩陣列向量化；λ表示來波波長。

1 陣列接收信號模型

陣列模型如圖1所示：L型嵌套陣由兩個相互正交的2階嵌套陣構成，x軸天線陣列和y軸天線陣列均由陣元數為N-1、陣元間隔為d=λ/2的均勻線陣，以及陣元數為N、陣元間隔為Nd的均勻線陣構成；x軸天線陣列的陣元位置為p=[ξd,0,0]，y軸天線陣列的陣元位置為q=[0,ξd,0]，ξ={0,1,…,N-2,N-1,…,N2-1}，原點處公共陣元為參考陣元。

圖1 L型嵌套陣列結構圖Fig.1 Array configuration of L-shaped nested array

圖1中：si(t)表示第i個入射信號，i=1，…，k，k為獨立遠場窄帶信號的個數；θ=[θ1,θ2,…,θk]表示入射信號的俯仰角；φ=[φ1,φ2,…,φk]表示入射信號的方位角；α=[α1,α2,…,αk]表示入射信號與x軸之間的夾角；β=[β1,β2,…,βk]表示入射信號與y軸之間的夾角。設空間存在的k個獨立遠場窄帶信號入射到陣列上，陣列輸出噪聲為0均值、σ2方差的高斯白噪聲。為了方便計算，在如下公式中用(α,β)代替(θ,φ)，角度轉換關系如(1)式所示：

cosα=cosθsinφ，
cosβ=sinθsinφ.

(1)

x軸天線陣列接收到的信號向量可以表示為

X(t)=[x1(t),x2(t),…,x2N-1(t)]T=
Ax(α)S(t)+Nx(t)，

(2)

式中：Ax(α)=[ax(α1),ax(α2),…,αx(αi)，…,ax(αk)]為x軸陣列的方向矩陣，其中

ax(αi)=[1,…,e-jπ(N-1)cos αi,…,e-jπ(N2-1)cos αi]T；

(3)

S(t)=[s1(t),s2(t),…,sk(t)]T為入射信號源向量；Nx(t)為x軸陣列接收到的高斯白噪聲向量。

y軸天線陣列接收到的信號向量可以表示為

Y(t)=[y1(t),y2(t),…,y2N-1(t)]T=
Ay(β)S(t)+Ny(t)，

(4)

式中：Ay(β)=[ay(β1),ay(β2),…,ay(βi)，…,ay(βk)]為y軸陣列的方向矩陣，其中

ay(βi)=[1,…,e-jπ(N-1)cos βi,…,e-jπ(N2-1)cos βi]T；

(5)

Ny(t)為y軸陣列接收到的高斯白噪聲向量。

2 基于L型嵌套陣的二維DOA估計算法

2.1 基于互協方差的虛擬陣列生成

2.1.1x軸虛擬陣列生成

x軸陣列劃分為兩個子陣,子陣1為x軸陣列前N個陣元組成的陣元間隔為λ/2的均勻線陣，其接收信號為

X1(t)=[x1(t),x2(t),…,xN(t)]T=
Ax1(α)S(t)+Nx1(t)，

(6)

式中：Nx1(t)為子陣1接收到的噪聲向量；Ax1(α)=[ax1(α1),ax1(α2),…,ax1(αi)，…，ax1(αk)]為子陣1的方向矩陣，其中

ax1(αi)=[1,e-jπcos αi，…,e-jπ(N-1)cos αi]T.

(7)

子陣2為x軸上第N個陣元到第2N-1個陣元組成的陣元間隔為Nλ/2的均勻線陣，其接收信號為

X2(t)=[xN(t),xN+1(t),…,x2N-1(t)]T=
Ax2(α)S(t)+Nx2(t)，

(8)

式中：Nx2(t)為子陣2接收到的噪聲向量；Ax2(α)=[ax2(α1),ax2(α2),…,ax2(αi),…,ax2(αk)]為子陣2的方向矩陣，其中

ax2(αi)=
[e-j(N-1)πcos αi,e-j(2N-1)πcos αi,…,e-j(N2-1)πcos αi]T.

(9)

子陣1的接收信號逆向排序，

X1z(t)=∏NX1(t)=
[xN(t),xN-1(t),…,x1(t)]T=
Ax1z(α)S(t)+Nx1z(t)，

(10)

式中：Ax1z(α)=[ax1z(α1),ax1z(α2),…,ax1z(αi),…,ax1z(αk)]，ax1z(αi)=[e-jπ(N-1)cos αi，e-jπ(N-2)cos αi,…,1]T。

逆向排序后的子陣1接收信號和子陣2接收信號進行互協方差運算，得到互協方差矩陣Rcx：

(11)

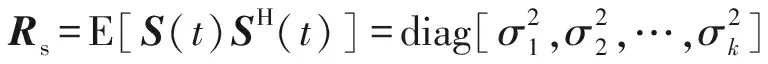
互協方差矩陣Rcx向量化，按列拉伸成1個N2×1階的長向量，表達式如下：

(12)

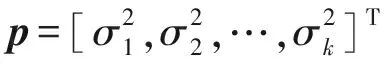
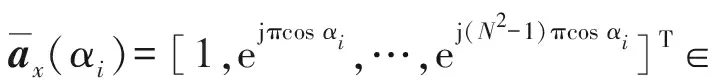
(13)

2.1.2y軸虛擬陣列生成

y軸上的陣元劃分為兩個子陣,子陣3為y軸上前N個陣元組成的陣元間隔為λ/2的均勻線陣，子陣4為y軸上第N個陣元到第2N-1個陣元組成的陣元間隔為Nλ/2的均勻線陣，其接收信號為

Y1(t)=[y1(t),y2(t),…,yN(t)]T=
Ay1(β)S(t)+Ny1(t)，

(14)

Y2(t)=[yN(t),yN+1(t),…,y2N-1(t)]T=
Ay2(β)S(t)+Ny2(t)，

(15)

式中：Ny1(t)、Ny2(t)分別為子陣3和子陣4接收到的噪聲向量；Ay1(β)=[ay1(β1),ay1(β2),…,ay1(βi),…,ay1(βk)]為子陣3的方向矩陣，

ay1(βi)=[1,e-jπcos βi，…,e-j(N-1)πcos βi]T；

(16)

接收信號Ay2(β)=[ay2(β1),ay2(β2),…,ay2(βi),…,ay2(βk)]為子陣4的方向矩陣，

ay2(βi)=
[e-j(N-1)πcos βi,e-j(2N-1)πcos βi,…,e-j(N2-1)πcos βi]T.

(17)

子陣3的接收信號逆向排序得到Y1z(t)，將Y1z(t)與子陣4的接收信號Y2(t)進行互協方差運算，得到互協方差矩陣Rcy. 由于不同子陣噪聲不相關，互協方差矩陣中的噪聲項被消除。

(18)

式中：Ay1z(β)=[ay1z(β1),ay1z(β2),…,ay1z(βi),…,ay1z(βk)]，ay1z(βi)=[e-j(N-1)πcos βi,e-j(N-2)πcos βi,…,1]T.

互協方差矩陣Rcy向量化，按列拉伸成1個N2×1階的長向量，表達式如下：

(19)

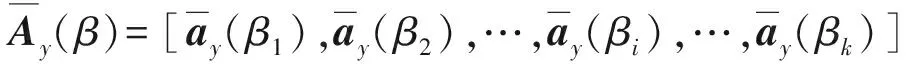
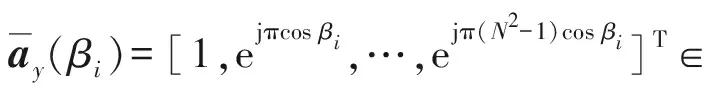
(20)

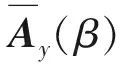
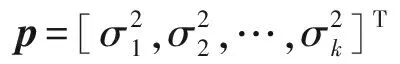
2.2 基于共軛矩陣的協方差矩陣構造

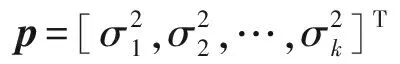
定義x軸的虛擬陣列接收信號為

(21)

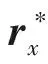
(22)

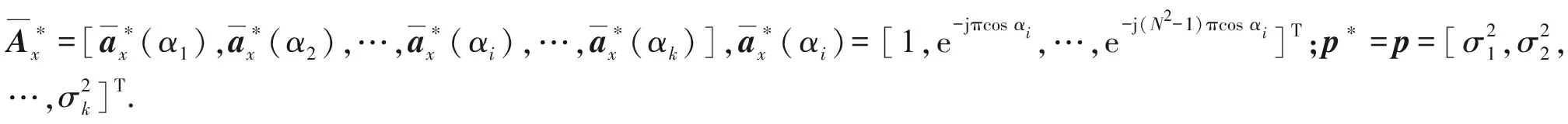
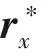
(23)

(24)

針對X1和X2，利用ESPRIT算法求解角度α，構造如下矩陣：

(25)

對矩陣Cx進行奇異值分解，得到k個大特征值對應的特征向量構成的矩陣Ex：

(26)

式中：T為k×k階的滿秩矩陣。利用虛擬陣列信號的旋轉不變性可得Ωx(α)：

(27)

由(27)式可知，對Ωx(α)進行特征值分解可得特征值u，即可得到角度，

=arccos(arg(u)/π).

(28)

同理，定義y軸的虛擬陣列接收信號為ry:

(29)

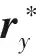
(30)

(31)

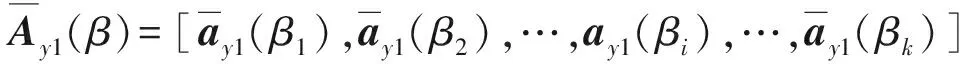
同理，針對Y1和Y2，利用ESPRIT算法求解角度β，構造如下矩陣：

(32)

由(26)式、(27)式，同理對矩陣Cy進行奇異值分解，可以求得Ωy(β)，對Ωy(β)進行特征值分解可得特征值v，即可得到角度：

=arccos(arg(v)/π).

(33)

2.3 角度匹配

由(28)式、(33)式可知，本文所提算法的兩個角度估計值和是通過兩次一維DOA估計得到的，角度和擔的估計值是失配的。本文提出利用虛擬陣列等效信源向量的唯一性進行角度匹配。采用(28)式得到的角度重構x軸方向虛擬陣列的方向矩陣由(12)式可知信源向量p可由陣列方向矩陣和虛擬陣列信號rx估計得到。通過最小二乘法可得信源向量的估計值1：

(34)

(35)

(36)

(37)

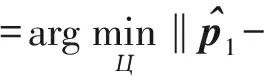
(38)

=Ц.

(39)

本文所提算法具體計算步驟如下：

1)x軸和y軸上的陣元分別劃分為兩個子陣，其接收信號分別為X1、X2和Y1、Y2，將X1和Y1逆向排序得到X1z、Y1z，將X1z和X2進行互相關運算得到Rcx，將Y1z和Y2進行互相關運算得到Rcy；

2) 由(12)式、(19)式，利用互協方差矩陣Rcx和Rcy向量化產生虛擬陣列信號rx和ry，等效信號源為全相干實包絡信號；

3) 利用虛擬陣列信號及其共軛矩陣構造滿秩的Toeplitz矩陣，作為等效協方差矩陣實現解相干，基于ESPRIT算法得到目標角度的估計值和；

2.4 算法分析

常規嵌套陣列利用自協方差矩陣產生的虛擬陣列存在冗余陣元，需要對產生的虛擬陣列進行去冗余處理。去冗余后的虛擬陣列信號為相干等價信號，需要進行解相干處理。對于M個陣元的二級嵌套陣列，采用空間平滑[23]、矩陣重構等方法進行解相干處理后，可估計的最大信源數Kmax為

(40)

根據(13)式、(20)式可知，本文所提算法利用M個陣元二級嵌套陣不同子陣信號的互協方差矩陣生成了無冗余陣元的虛擬陣列，消除了噪聲。針對虛擬陣列等效信號轉化為相干信號，本文利用虛擬陣列及其共軛矩陣構造滿秩的等效協方差矩陣實現了解相干，由[23]式、[24]式、[30]式、[31]式可知，可估計的最大信源數為M2/4+M/2-3/4，與利用自協方差矩陣的嵌套陣列最大可估計信源數相同，優于文獻[16]、文獻[18]、文獻[19]中可估計的最大信源數M-1.

通過以上分析可知，本文所提算法的主要計算復雜度包括互協方差矩陣運算、矩陣奇異值分解、最小二乘法，所提算法涉及到的復數乘法次數為O[(M+1)2L/2+4((M+1)2/4-1)3+3k2(M+1)+3k3，其中k表示信源數，L表示快拍數。文獻[16]利用互協方差矩陣進行聯合奇異值分解(JSVD)算法需要波束形成進行角度搜索，假設搜索范圍為[0°,180°]，搜索步長為0.01°，其算法復雜度為O[M2L+8M3+18 000M2]；文獻[18]中所需的復數乘法次數為O[M2L+3M3+2M4]；文獻[19]中所需的復數乘法次數為O[M2L+2k3+(7M-4)k2+k(M-1)(2M-k)]。

圖2所示為本文所提算法與文獻[16]、文獻[18]、文獻[19]所提算法的復雜度對比圖。從圖2中可以看出，本文所提算法無需進行角度搜索，計算復雜度低于文獻[16]。但由于產生了更多的虛擬陣元，增大了角度自由度，本文所提算法的計算復雜度高于文獻[18-19]。

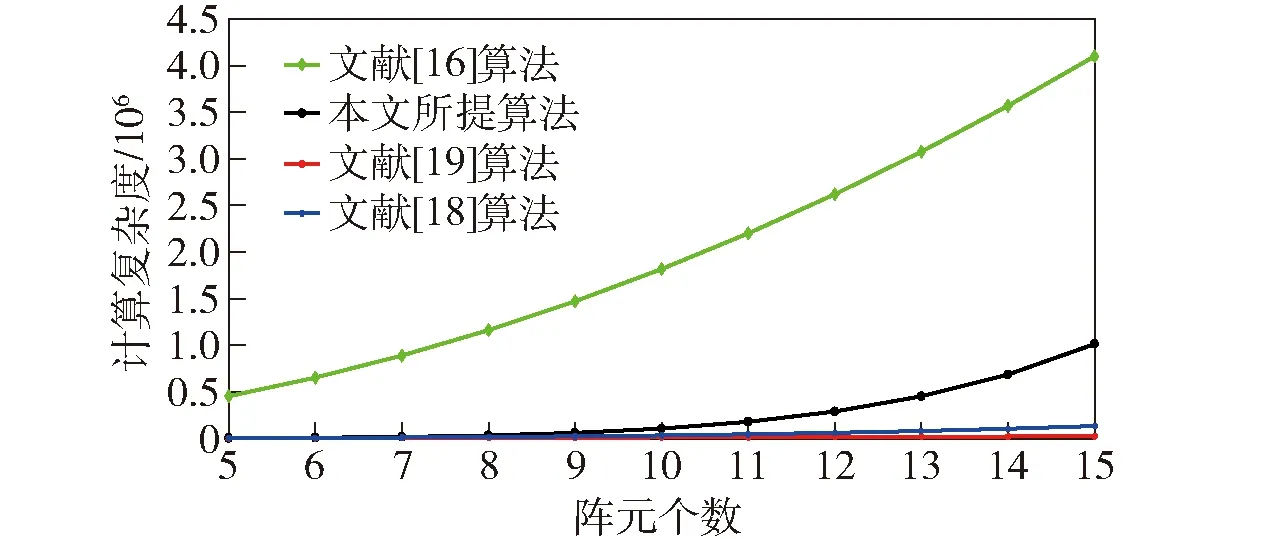
圖2 算法復雜度與陣元個數關系Fig.2 Algorithm complexity versus number of array elements

3 仿真實驗及性能分析

為了驗證本文方法的有效性，本文進行系列仿真實驗，分析比較本文所提算法以及文獻[16]、文獻[18]、文獻[19]中算法的估計性能，仿真實驗中陣元間隔為半波長。采用均方根誤差、角度分辨概率衡量DOA估計性能，如(41)式、(42)式所示：

(41)

(42)

為了驗證所提算法的有效性，下面通過仿真實驗分別分析所提算法的DOA估計性能、DOA估計性能與信噪比的關系，以及DOA估計性能與入射信源數的關系。

1) 仿真1.x軸方向陣元和y軸方向陣元個數均為9，子陣1～子陣4的陣元個數均為5，3個獨立窄帶遠場的信號入射到陣列上，其入射信號角度(α,β)分別為(20°,10°)、(50°,40°)、(60°,50°)，快拍數為100，信噪比SNR分別為0 dB、5 dB、10 dB，進行200次Monte Carlo仿真實驗。

圖3、圖4、圖5分別表示信噪比SNR為0 dB、5 dB、10 dB時本文所提算法的估計結果。從圖中可以看出，在信噪比分別為0 dB、5 dB、10 dB時，本文所提方法均成功實現了空間信源的方向估計，表明該算法可以在低信噪比環境下有效地進行DOA估計。

圖3 SNR=0 dB的估計結果Fig.3 DOA estimated results for SNR=0 dB

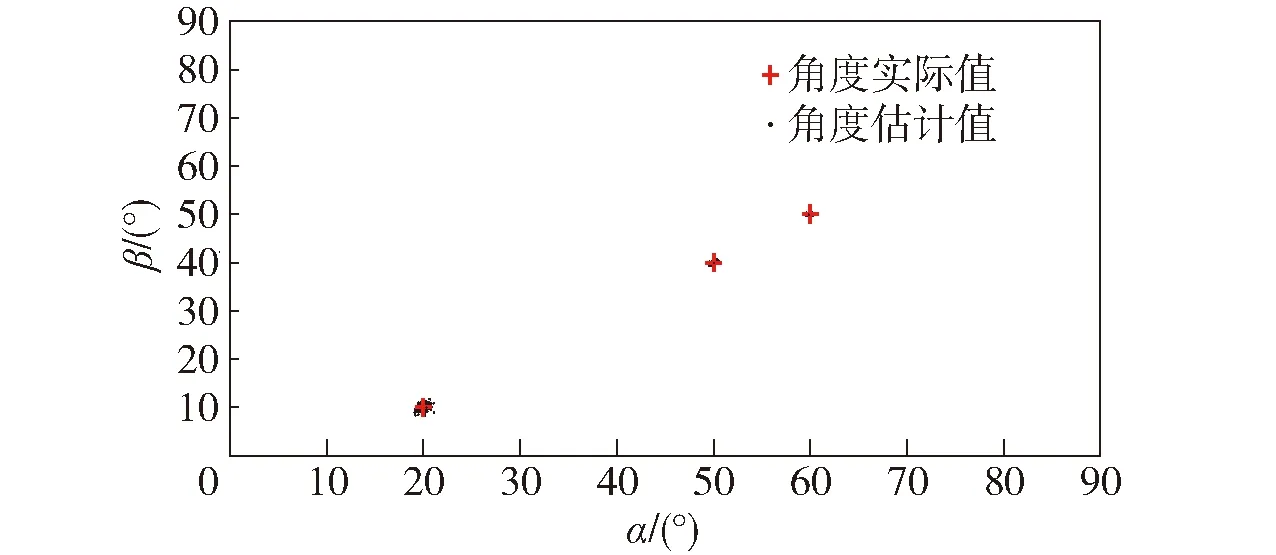
圖4 SNR=5 dB的估計結果Fig.4 DOA estimated results for SNR=5 dB

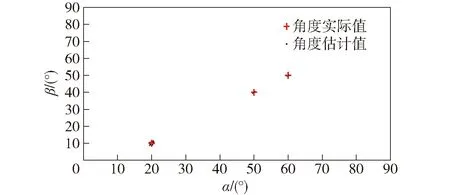
圖5 SNR=10 dB的估計結果Fig.5 DOA estimated results for SNR=10 dB

2) 仿真2.x軸方向和y軸方向陣元個數均為9，子陣1～子陣4的陣元個數均為5，3個獨立窄帶遠場信號入射到陣列上，其入射信號角度(α,β)分別為(25°,10°)、(50°,45°)、(60°,55°)，信噪比SNR為0～20 dB，進行200次Monte Carlo仿真實驗。圖6所示為本文所提算法以及文獻[16]、文獻[18]、文獻[19]算法的DOA估計均方根誤差與信噪比的關系圖。圖7所示為本文所提算法以及文獻[16]、文獻[18]、文獻[19]算法的角度分辨概率與信噪比的關系圖。

圖6 均方根誤差與信噪比關系圖(快拍數為100)Fig.6 RMSE versus SNR (Snapshots=100)

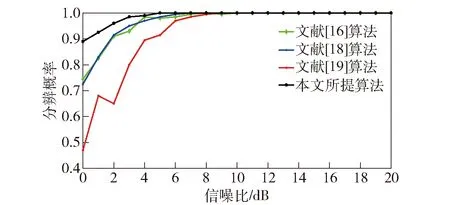
圖7 分辨概率與信噪比關系圖(快拍數為100)Fig.7 Angular resolution probability versus SNR (Snapshots=100)

從圖6、圖7中可以看出，本文所提算法的DOA估計均方根誤差遠小于文獻[16]、文獻[18]、文獻[19]算法，而角度分辨概率分別優于文獻[16]、文獻[18]、文獻[19]算法，表明本文所提算法的DOA估計性能優于文獻[16]、文獻[18]、文獻[19]算法。當信噪比SNR=0時，本文所提算法的均方根誤差小于1°，角度分辨概率接近90%，表明本文所提算法在低信噪比環境下具有較高的估計性能。隨著信噪比SNR的升高，本文所提算法與文獻[16]、文獻[18]、文獻[19]算法相比，其均方根誤差變化較為平緩，表明本文所提算法對空間噪聲具有更強的魯棒性。

3) 仿真3.x軸方向和y軸方向陣元個數均為9，子陣1～子陣4的陣元個數均為5，入射到陣列上的信源數為1～10，入射角度(α,β)依次為(25°,30°)、(35°,40°)、(45°,50°)、(55°,60°)、(65°,70°)、(75°,80°)、(85°,90°)、(95°,100°)、(105°,110°)、(115°,120°)，信噪比SNR為10 dB，快拍數為100，進行500次Monte Carlo仿真實驗。圖8所示為本文所提算法以及文獻[16]、文獻[18]、文獻[19]算法的DOA估計均方根誤差與入射信源數的關系。

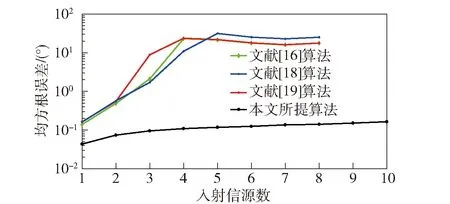
圖8 均方根誤差與入射信源數的關系圖 (快拍數為100)Fig.8 RMSE versus number of incident signals (Snapshots=100)

從圖8中可以看出，隨著入射信源數從1增加到4，文獻[16]、文獻[18]、文獻[19]算法與本文所提算法的DOA估計均方根誤差均增大。在入射信源數大于5、小于8時，文獻[16]、文獻[18]、文獻[19]算法的可估計最大信源數為M-1=8，此時入射信源數接近可估計最大信源數，算法的DOA估計均方根誤差不隨入射信源數的增大而增大。而本文所提算法的可估計最大信源數為M2/4+M/2-3/4=24，遠大于仿真中入射信源數的變化范圍，其DOA估計均方根誤差隨著入射信源數的增多緩慢增大，且本文所提算法的DOA估計均方根誤差明顯小于文獻[16]、文獻[18]、文獻[19]算法，表明隨著信源數的增多，本文所提算法的DOA估計性能優于文獻[16]、文獻[18]、文獻[19]中的算法。當信源數為9、10時，入射信源數已經大于文獻[16]、文獻[18]、文獻[19]算法的可估計最大信源數M-1=8，此時它們均已失效，而本文所提算法依然能夠正常工作。

4 結論

本文針對L型均勻陣列角度分辨率較低、可估計空間信源數受限于陣元數及估計精度易受到信噪比影響的問題，提出一種新的L型嵌套陣二維DOA估計算法。該方法利用不同子陣信號的互協方差矩陣產生虛擬陣列并消除了噪聲的干擾，利用虛擬陣列輸出信號及其共軛矩陣構建了等效協方差矩陣，通過ESPRIT算法分別獲得了角度α和β的估計值，利用虛擬陣列等效信源的唯一性實現了角度匹配。通過仿真實驗，將本文所提算法與文獻[16]、文獻[18]、文獻[19]算法進行了對比，仿真結果表明本文所提算法的估計性能明顯優于其他算法，具有更大的角度自由度，可以辨識更多的空間信源，在低信噪比環境下具有較高的DOA估計精度。本文所提算法在獲得更大角度自由度和更高估計精度的同時，不可避免地提高了算法的計算復雜度，在實際應用過程中需加以考慮。