基于獨立電驅動履帶車輛的地面參量估計方法研究

梁文利， 陳慧巖， 王博洋

(北京理工大學 機械與車輛學院， 北京 100081)

0 引言

影響混合動力履帶車輛機動性和通過性的因素有很多，包括發(fā)動機功率、電機功率、車輛質量、履帶寬度、履帶接地長等。除了上述車輛參數(shù)與空氣阻力的影響之外，地面條件也是影響履帶車輛行駛性能的主要因素。

國內(nèi)外很多研究者從速差轉向車輛轉向性能出發(fā)，建立了較為準確的履帶車輛動力學模型，并對車輛性能進行了分析或對地面參量進行了估計。早在2004年，Martinez等[1]就提出了履帶車輛的近似運動學模型并用于軌跡預測；程軍偉等[2]考慮了履帶車輛與地面之間的道路阻力系數(shù)和轉向阻力系數(shù)，建立了較為準確的履帶車輛滑移滑轉模型。

車輛行駛數(shù)據(jù)往往能較準確地反映地面狀況，因此對車輛行駛數(shù)據(jù)進行統(tǒng)計學分析，對于車輛- 地面系統(tǒng)的研究很有必要。文獻[3]利用在線稀疏高斯過程表征某滑移轉向的速度模型，并利用大量行駛數(shù)據(jù)對模型進行訓練。文獻[4]基于高斯混合- 隱馬爾可夫模型的統(tǒng)計學習方法建立駕駛員模型，并利用模型對下一時刻車輛的轉向模式做出預測。文獻[5-8]通過構建運動基元的方式，對獲得的大量試驗數(shù)據(jù)進行分類，并與控制量相聯(lián)系，從而輸出控制序列。

地面參數(shù)是地面特征的直接體現(xiàn)，對地面參數(shù)進行準確估計是優(yōu)化車輛行駛性能以及精確控制的基礎。文獻[9-10]提出的g算法可對3個土壤推力參數(shù)進行解耦和識別，并解決了利用貝克土壤理論進行地面參數(shù)估計所帶來的多解問題[11-12]。文獻[13]利用一套專用的測量裝置，通過直接測量履帶車輛兩側主動輪輸出轉矩的方法來計算履帶車輛行駛地面行駛的參數(shù)值。文獻[14]在不考慮滑移和滑轉情況下，利用設計制造的履帶模型車探究了松軟草地上模型車車速對直線行駛阻力的影響規(guī)律。文獻[15]根據(jù)地面力學理論對載荷比的影響因素進行了理論分析，并在車輛參數(shù)、行駛阻力系數(shù)一定條件下，通過土壤剪切試驗獲得了土壤參數(shù)值。文獻[16]通過研究某滑移轉向機器人平臺不同轉向半徑下的穩(wěn)態(tài)轉向過程，實現(xiàn)了轉向過程中地面參數(shù)的在線更新并建立了具有地面自適應性的車輛- 地面模型。

以上關于履帶車輛地面參量估計的研究主要集中在以下兩方面：一是基于貝克土壤理論的地面參數(shù)估值[9-12]，特點是涉及參數(shù)較多、計算量很大、效率低；二是通過設計專門的試驗設備或測試系統(tǒng)，結合車輛動力學模型進行地面參量估計[13-15]，特點是試驗過程復雜、精度不高。 基于此，本文提出一種依賴較少傳感器進行地面參量估計的方法，通過對車輛行駛數(shù)據(jù)進行統(tǒng)計學分析，進而建立驅動力統(tǒng)計學預測模型的方法，并結合履帶車輛動力學模型，對履帶車輛行駛過程中的地面參量進行估計。

1 主動輪轉矩預測值的生成

在進行地面參量估計過程中，首先需要提取車輛行駛數(shù)據(jù)，包括：采集時間t，左側主動輪轉速nl，右側主動輪轉速nr，航向角偏差Δθ，左側主動輪轉矩Tl，右側主動輪轉矩Tr(本文提到的左側或右側均為從車尾方向看；主動輪轉速、主動輪轉矩分別由電機轉速、電機轉矩以及電機與主動輪間的變速比求得)。通過路徑分割和建立運動基元的方式對提取到的行駛數(shù)據(jù)進行重新分組，并建立相應的驅動力統(tǒng)計學預測模型，將驅動力統(tǒng)計學預測模型與車輛動力學模型相結合進行地面參量估計。算法具體流程圖如圖1所示。

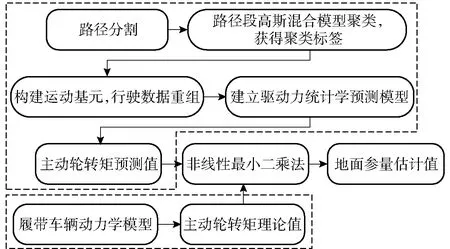
圖1 算法流程圖Fig.1 Algorithm flow chart

由圖1的流程生成主動輪轉矩預測值，首先需要進行路徑分割，然后基于路徑段的聚類標簽建立運動基元。

1.1 路徑分割模型以及運動基元的建立

在建立運動基元模型過程中，如圖2所示，先選取過零航向角偏差點作為路徑分割節(jié)點進行路徑分割，將車輛行駛路徑劃分為若干路徑段，其中選取第i段路徑的時間間隔td,i、平均航向角偏差Δθavei、最大航向角偏差Δθmaxi以及左主動輪平均轉速nlavei，右主動輪平均轉速nravei作為表征數(shù)據(jù)，具體表示為

pathi=[td,i,Δθavei,Δθmaxi,nlavei,nravei].

(1)

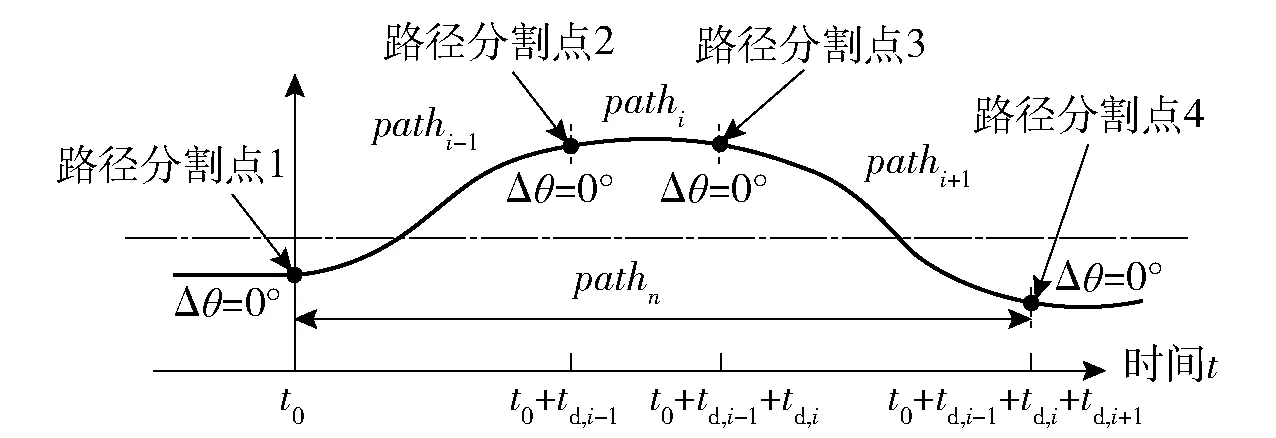
圖2 路徑分割以及運動基元的建立Fig.2 Path segmentation and establishment of motion primitives

利用高斯混合模型(GMM)對上述提取到的數(shù)據(jù)進行多元聚類，得到路徑分割模型path. 多變量GMM可以表示為

(2)

式中：G(x)為變量x的高斯分布；K為路徑段高斯分量的數(shù)目；pi為各高斯分量的先驗概率值；

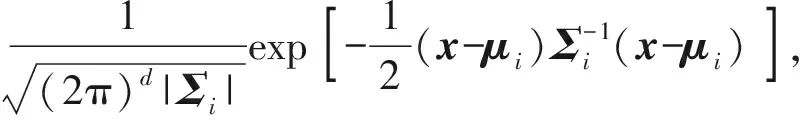
(3)

d為變量x的數(shù)據(jù)維度，利用極大似然估計和最大期望(EM)算法可得到各高斯分量的參數(shù)值，μi為各高斯分量的中心點矩陣，Σi為各高斯分量的協(xié)方差矩陣。

在建立GMM過程中 ，聚類個數(shù)以及聚類初始參數(shù)的確定十分關鍵。首先，選取不同行駛工況下的部分數(shù)據(jù)組成數(shù)據(jù)集Z，針對不同的聚類數(shù)目K，對Z進行多次K-means聚類，對于Z中的數(shù)據(jù)點i，計算其輪廓系數(shù)si，輪廓系數(shù)越接近1，說明對于該數(shù)據(jù)點的聚類結果越合理。計算Z中所有數(shù)據(jù)點的輪廓系數(shù)并求其平均值，選取平均輪廓系數(shù)最接近1的K值對應的聚類結果作為GMM的初始化參數(shù)。然后，利用EM算法對模型進行訓練，從而得到需要的路徑段GMM，其參數(shù)即為所求的pi、μi、Σi. 其中第i段路徑的聚類標簽可以表示為

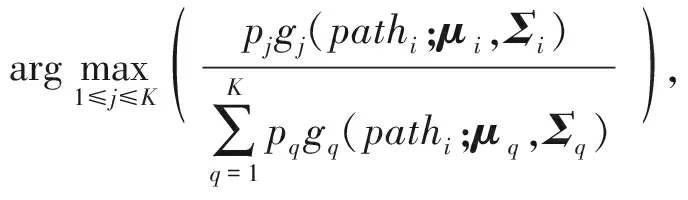
(4)

運動基元表示為

pathn=
[label_pathi-1,label_pathi,label_pathi+1]，

(5)

式中：1≤n≤K1，K1表示運動基元種類數(shù)。圖3所示為運動基元的建立過程。

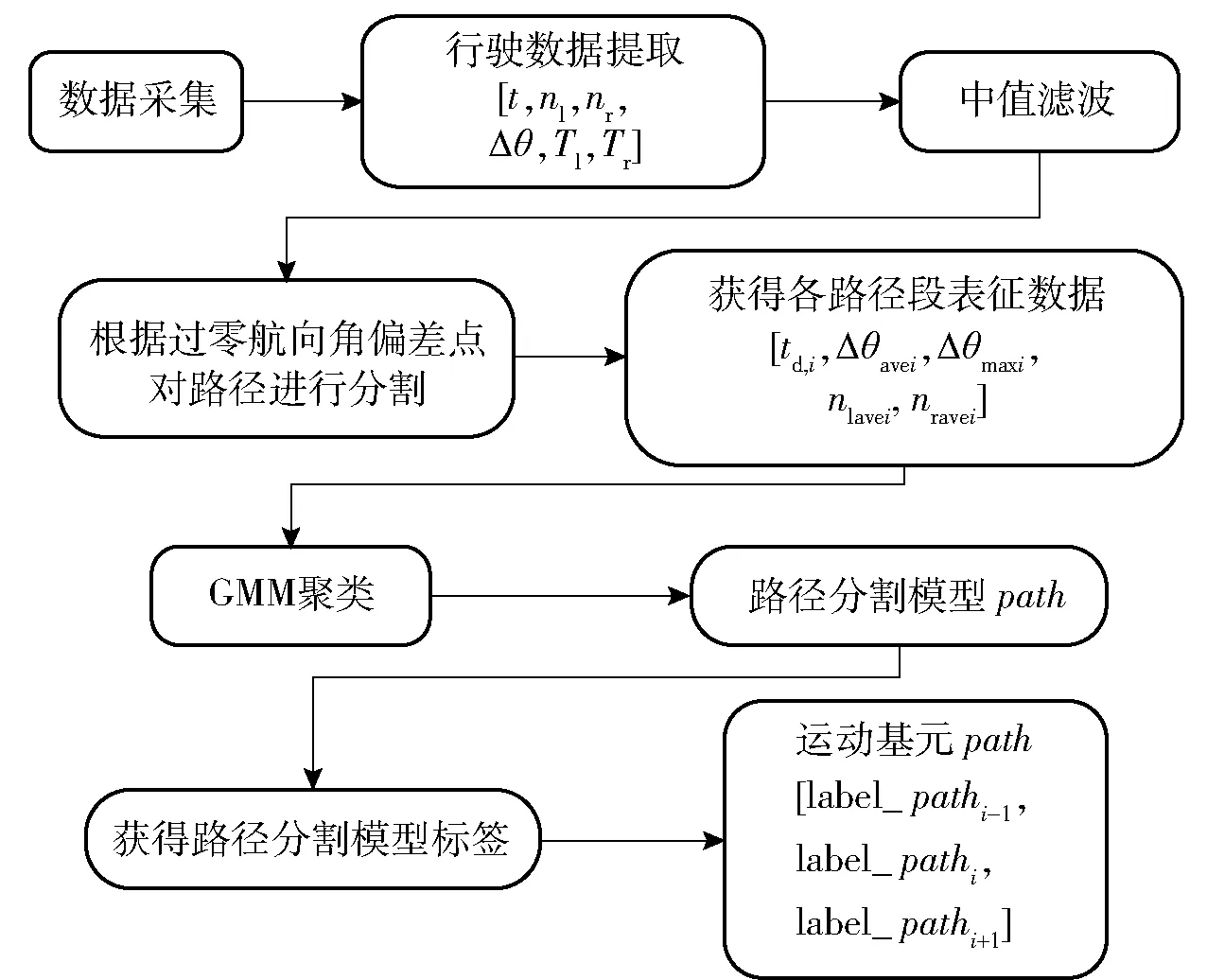
圖3 運動基元建立過程Fig.3 Establishing process of motion primitives

1.2 建立驅動力統(tǒng)計學預測模型

在建立驅動力統(tǒng)計學預測模型過程中，以運動基元類型為依據(jù)對數(shù)據(jù)進行分組，基于分組后的數(shù)據(jù)，利用GMM構建驅動力統(tǒng)計學預測模型，因此建立的驅動力統(tǒng)計學預測模型與運動基元是一一對應的。驅動力統(tǒng)計學預測模型用到的車輛行駛數(shù)據(jù)以及表示形式為

Modeln=[nlΔtn,nrΔtn,ΔθΔtn,TlΔtn,TrΔtn],

(6)

式中：下標Δtn為訓練集數(shù)據(jù)中第n類運動基元所占的總行駛時間；nlΔtn、nrΔtn、ΔθΔtn、TlΔtn、TrΔtn分別為Δtn時間范圍內(nèi)的兩側主動輪轉速、航向角偏差以及兩側主動輪轉矩，其中nlΔtn、nrΔtn、ΔθΔtn為模型輸入，TlΔtn、TrΔtn為模型輸出。利用GMM聚類建立驅動力統(tǒng)計學預測模型時，初始值確定和參數(shù)估計過程與1.1節(jié)相同。圖4所示為驅動力統(tǒng)計學預測模型的建立過程。

圖4 驅動力統(tǒng)計學預測模型建立過程Fig.4 Establishing process of driving force statistical models

驅動力統(tǒng)計學預測模型可看作在大量試驗數(shù)據(jù)基礎上建立的車輛- 地面關系模型，其中的輸入量代表車輛系統(tǒng)，輸出量受地面約束，與地面參數(shù)有關。當驅動力統(tǒng)計學預測模型以及輸入量確定后，高斯混合回歸(GMR)算法可以用來預測模型中的輸出量，即兩側主動輪轉矩。

1.3 基于GMR的主動輪轉矩預測

當運動基元類型即n值確定后，就可確定對應的驅動力統(tǒng)計學預測模型，假設其聚類個數(shù)為K2，高斯分量k的均值矩陣和協(xié)方差矩陣則可以表示為

μk={μin,k,μes,k}，1≤k≤K2，

(7)

(8)

式中：μin,k、Σin,k、μes,k、Σes,k分別為輸入值和估計值的均值矩陣和方差矩陣；Σines,k為輸入值與估計值的協(xié)方差矩陣；Σesin,k為估計值與輸入值的協(xié)方差矩陣。并且有

es,k=μes,k+Σesin,k(Σin,k)-1(Din-μin,k)，

(9)

es,k=Σes,k-Σesin,k(Σin,k)-1Σines,k，

(10)

式中：Din為輸入量。

同時，對于輸入量Din，其屬于高斯分量k的概率為

(11)

最終輸出量的預測值以及方差可以看作各高斯分量的混合，即

(12)

(13)

主動輪轉矩預測過程如圖5所示。

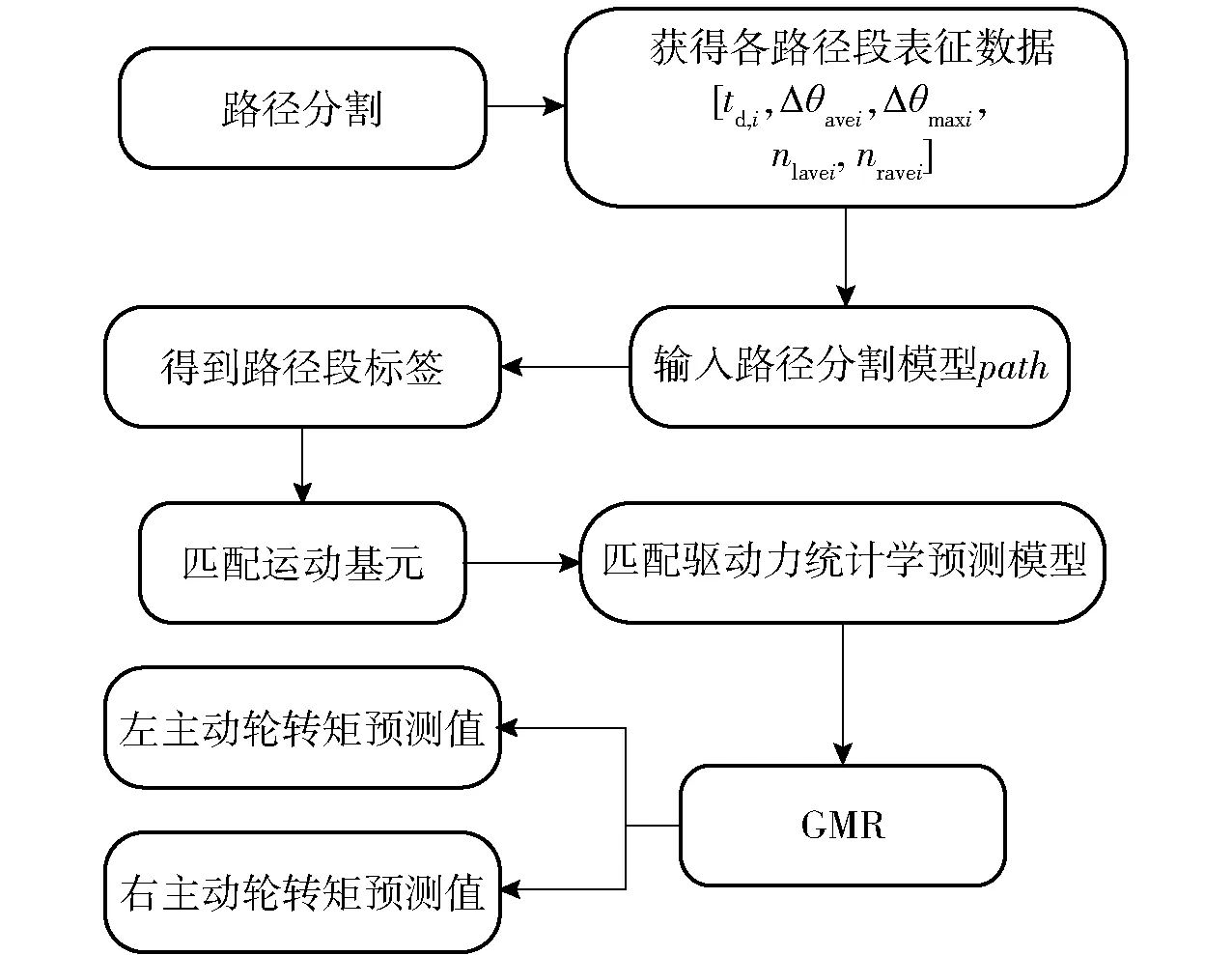
圖5 主動輪轉矩預測過程Fig.5 Predictiing process of driving wheel torque

2 地面參量求解過程

本文所研究的地面參量為行駛阻力系數(shù)以及轉向阻力系數(shù)，在進行地面參量估計時，需要引入履帶車輛的動力學模型作為主動輪轉矩理論值的生成依據(jù)。下文中以下標i代表內(nèi)側履帶，下標o代表外側履帶。

結合文獻[2，17]，履帶車輛兩側主動輪理論轉矩與地面參量之間的關系可表示為

(14)

式中：Ti、To為兩側主動輪理論轉矩；m為車輛質量；r為履帶車輛主動輪半徑；f為道路阻力系數(shù)；轉向阻力系數(shù)μ=μmax/(0.925+0.15R/B)，R為轉向半徑，B為履帶中心距，μmax為履帶車輛轉向半徑R=B/2時的轉向阻力系數(shù)；ai=Ai/(L/2)，ao=Ao/(L/2)，Ai、Ao分別為內(nèi)側、外側履帶轉向極的橫向偏移量，即內(nèi)側、外側履帶接地段的瞬時轉向中心到內(nèi)側、外側履帶縱向軸線的距離，L為履帶接地段長度；g為重力加速度；式中負號表示方向與車輛行駛方向相反。

假設根據(jù)驅動力統(tǒng)計學預測模型預測得到的兩側主動輪轉矩分別為T′i、T′o，預測值個數(shù)為N. 利用非線性最小二乘法優(yōu)化算法求解地面參數(shù)的流程如下：

步驟1根據(jù)(14)式，將含有f、μ的主動輪理論轉矩表達式以及T′i、T′o代入(15)式：

(15)

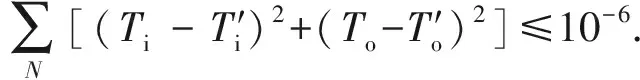
地面參量求解過程如圖6所示。

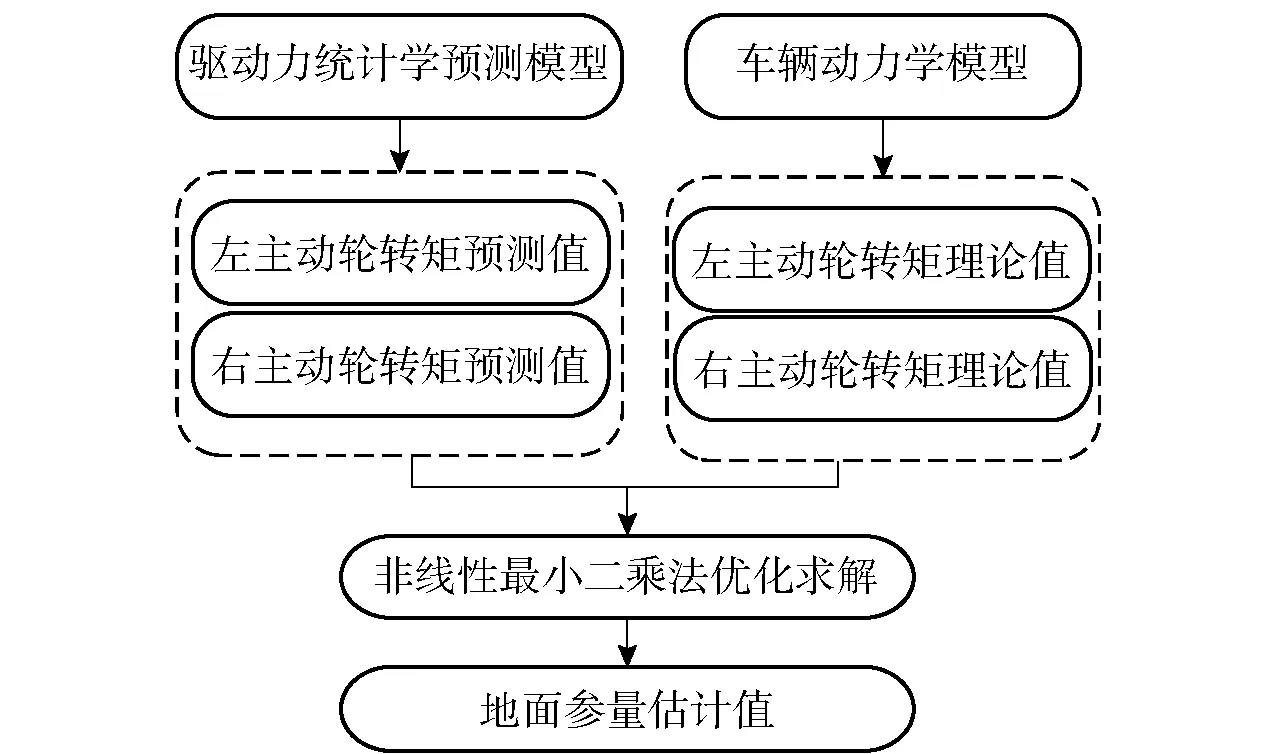
圖6 地面參量求解過程Fig.6 Solving process of ground parameters

3 行駛數(shù)據(jù)分析

本文研究對象為獨立電驅動履帶車輛，由兩側電機帶動主動輪，進而為車輛提供動力且兩電機相互獨立。為了得到某一路面對應的參數(shù)特性，采集履帶車輛在該路面下不同行駛工況的數(shù)據(jù)，包括不同速度下的車輛直駛工況、S彎工況、換道工況、定半徑轉向工況等。為排除試驗過程中的偶然誤差，每類試驗均重復多組，提取數(shù)據(jù)中的電機轉速、車輛航向角以及電機轉矩信息，其中電機轉速以及電機轉矩數(shù)據(jù)均為電機控制器的反饋量，航向角由慣性導航系統(tǒng)與全球定位系統(tǒng)組合定位系統(tǒng)測量得到。去除冗余數(shù)據(jù)(主要包括靜止狀態(tài)數(shù)據(jù))并進行中值濾波處理；航向角偏差由下一時刻車輛航向角減去本時刻車輛航向角求得。將試驗數(shù)據(jù)分為訓練集和測試集，根據(jù)圖3所示流程，利用訓練集中車輛的過零點航向角偏差將路徑分割為多個路徑段，并進行GMM聚類，得到路徑分割模型path，表1所示為路徑分割模型的表征數(shù)據(jù)。

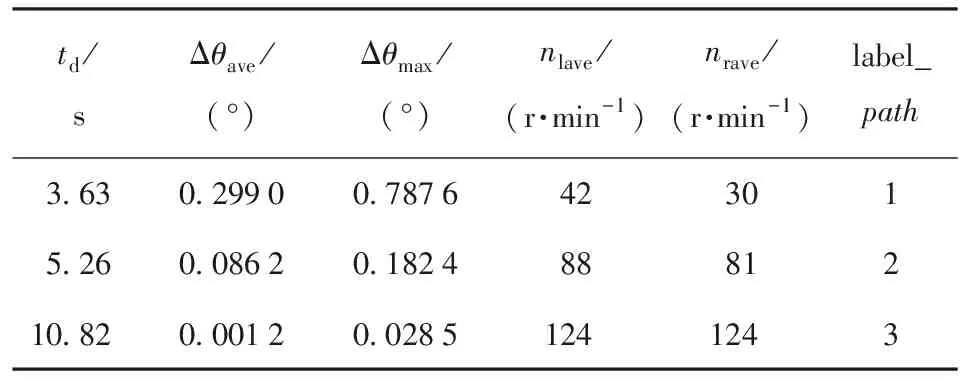
表1 路徑段聚類結果

剔除出現(xiàn)概率較小的運動基元，建立的運動基元共分為8類，即K1=8，對應的路徑段的標簽組成以及所占比例如表2所示。

根據(jù)建立的運動基元對行駛數(shù)據(jù)進行重組，并根據(jù)圖4利用GMM聚類建立相應的驅動力統(tǒng)計學預測模型。

為了驗證驅動力統(tǒng)計學模型對兩側主動輪轉矩的預測效果，根據(jù)圖5所示流程，得到兩側主動輪轉矩的預測值，將預測值與實際值進行比較，對比結果如圖7和圖8所示。

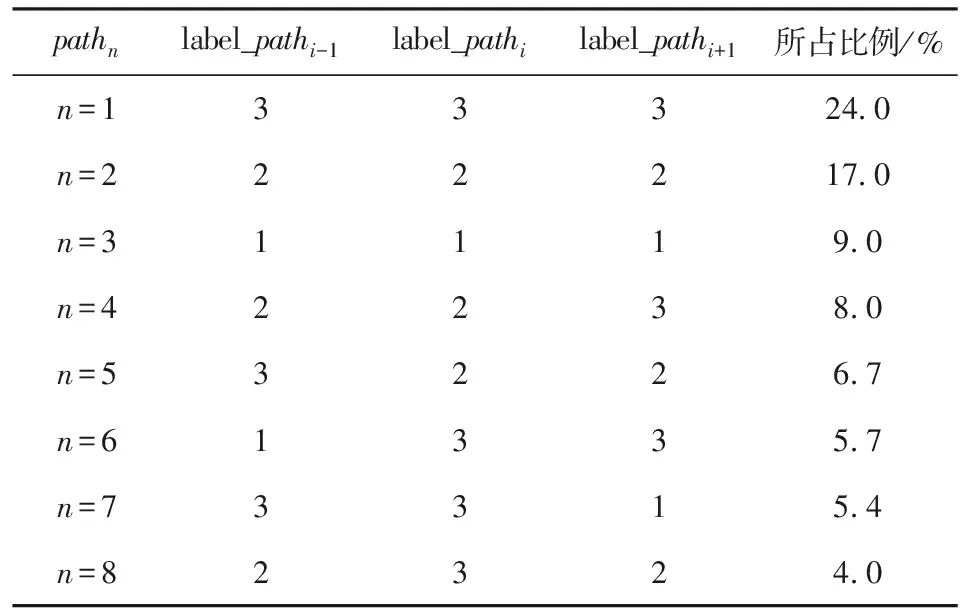
表2 運動基元生成結果

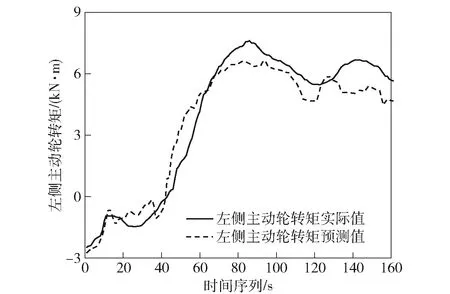
圖7 左側主動輪轉矩預測值與實際值對比Fig.7 Comparison of predicted and actual values of the left driving wheel torque

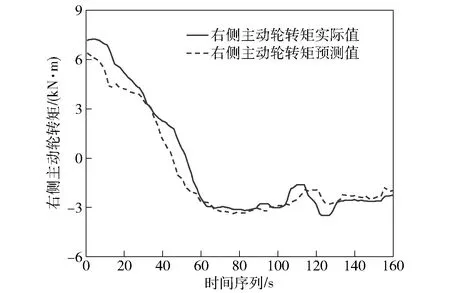
圖8 右側主動輪轉矩預測值與實際值對比Fig.8 Comparison of predicted and actual values of the right driving wheel torque

由上述預測結果可知，本文所建立的驅動力統(tǒng)計學預測模型可以較準確地預測車輛在行駛過程中兩側主動輪轉矩的變化。

4 實車試驗

為了驗證算法的有效性，在某平坦土路上(該路面與之前采集訓練數(shù)據(jù)的地面一致)進行實車試驗。試驗車輛由某型號履帶車輛改造而來，發(fā)動機通過燃燒燃油帶動發(fā)電機工作，發(fā)電機將發(fā)出的電能與動力電池組中的電能進行混合，共同驅動兩側驅動電機，兩側驅動電機再通過2擋自動變速箱以及輪邊減速器減速(自動變速箱1擋變速比為2.7，2擋變速比為1.0，數(shù)據(jù)均在1擋下采集；輪邊減速比為5.5)，帶動主動輪轉動，最后推動平臺運動。車輛總質量10 000 kg，履帶接地段長度L=3.095 m，履帶中心距B=2.464 m，主動輪半徑r=0.265 4 m. 圖9所示為試驗車輛及路面。

圖9 試驗車輛及路面Fig.9 Test tracked vehicle and experimental road

試驗過程中駕駛員操縱車輛，使車輛進行以下4種類型試驗：

第1類：連續(xù)變半徑轉向試驗，記錄車輛行駛過程中的電機轉速、航向角以及電機轉矩。根據(jù)慣性導航系統(tǒng)與全球定位系統(tǒng)組合定位系統(tǒng)得到每一時刻車輛的經(jīng)度和緯度坐標，經(jīng)轉換后得到某次試驗中車輛的實際運動軌跡如圖10所示。

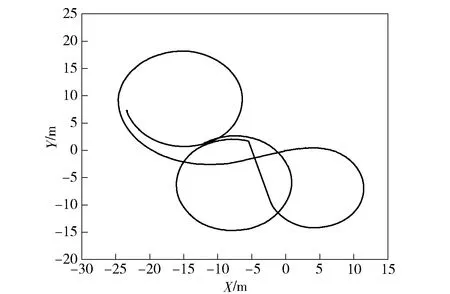
圖10 連續(xù)穩(wěn)態(tài)轉向的車輛行駛軌跡Fig.10 Vehicle trajectory during continuous steady-state steering

第2類：直駛與大半徑穩(wěn)態(tài)轉向試驗，使車輛先直駛一段時間后進行較大半徑的連續(xù)轉向，某次試驗中車輛的實際運動軌跡如圖11所示。

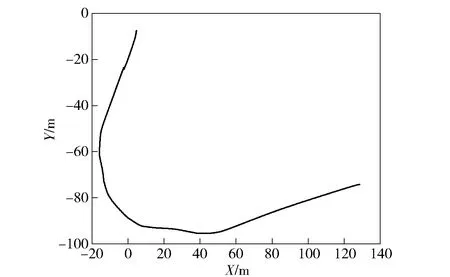
圖11 直駛轉大半徑轉向的車輛行駛軌跡Fig.11 Vehicle trajectory during straight driving and smooth radius steering

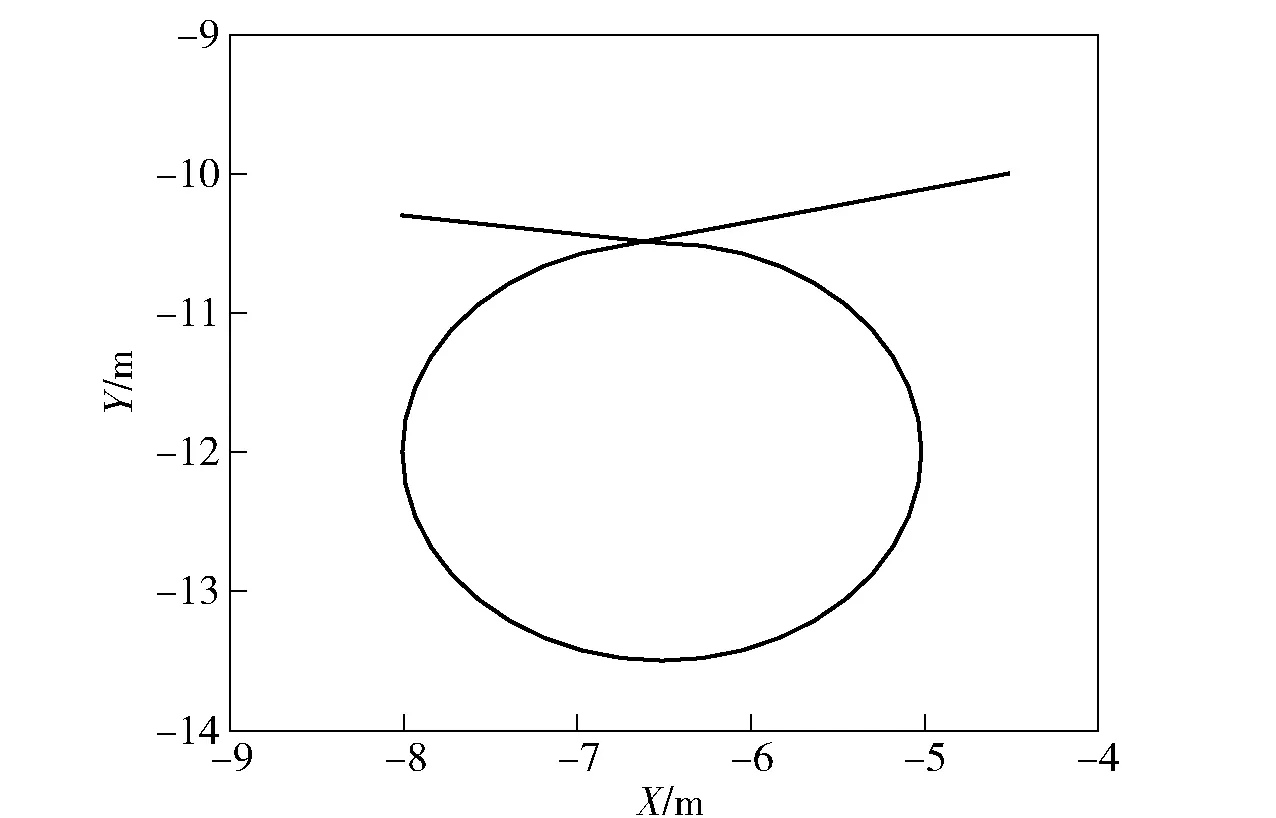
圖12 一側主動輪制動的車輛行駛軌跡Fig.12 Vehicle trajectory during driving wheel braking on one side

第3類：單側履帶制動的轉向試驗，使車輛保持一側電機制動，另一側電機保持恒定轉速，車輛的實際運動軌跡如圖12所示。

第4類：車輛滑行試驗，車輛以某一速度勻速直線行駛一段距離后，將兩側電機切換至自由轉模式，此時電機不再提供驅動力，根據(jù)滑行距離以及滑行前車速可以得到道路阻力系數(shù)f的測試值。試驗數(shù)據(jù)如表3所示。

假設車輛進行穩(wěn)態(tài)轉向時兩側主動輪轉矩實際值為T″i、T″o，將T″i、T″o代替T′i、T′o代入(15)式，利用最小二乘法迭代計算可得到轉向阻力系數(shù)μ的測試值與轉向半徑R的關系。

根據(jù)圖5所示流程，可以得到兩側主動輪轉矩預測值T′i、T′o，結合第2節(jié)地面參數(shù)的求解步驟，可得到地面參數(shù)μ、f的估計值。μ、f的估計值與測試值對比如圖13和圖14所示。

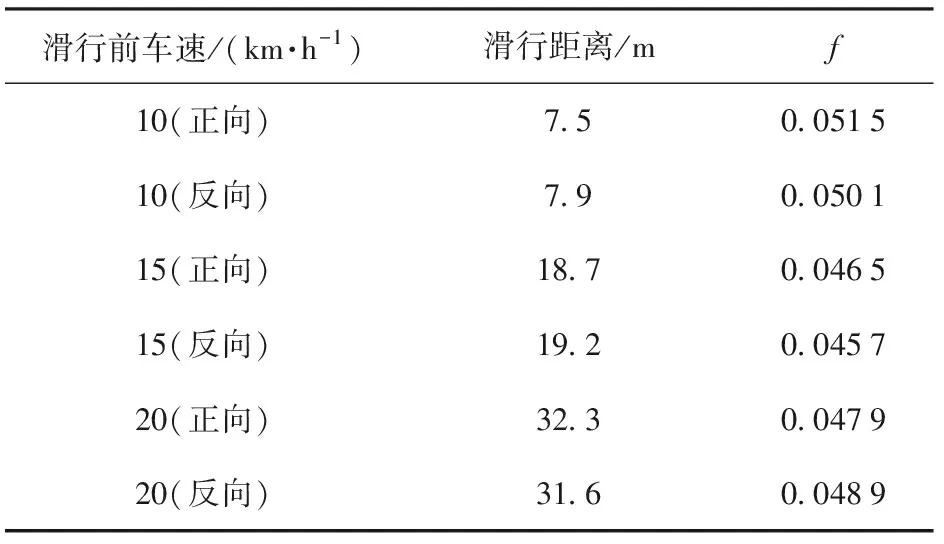
表3 滑行試驗數(shù)據(jù)以及處理結果

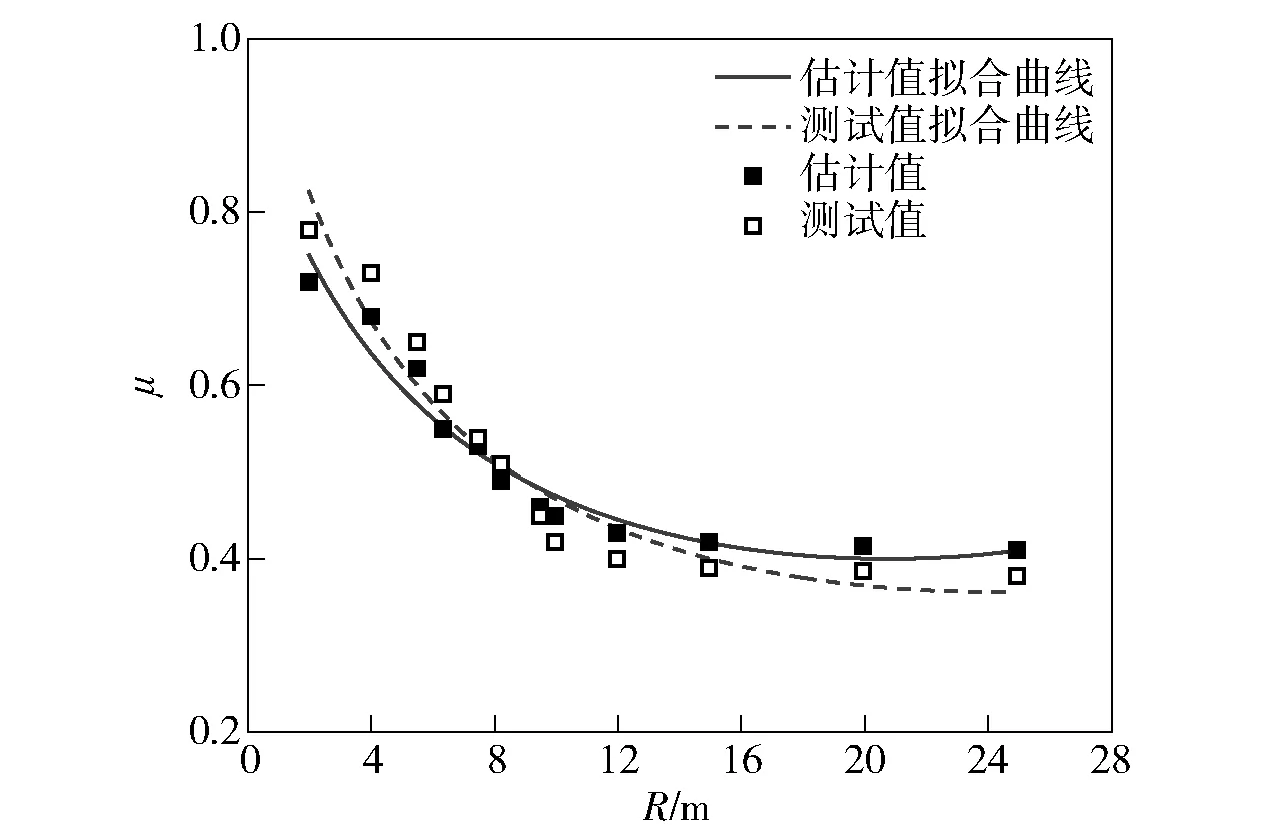
圖13 轉向阻力系數(shù)的估計值與測試值對比Fig.13 Comparison of estimated and test values of steering resistance coefficient

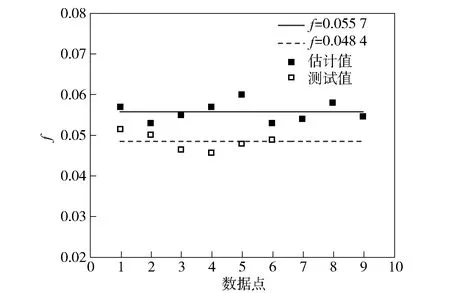
圖14 道路阻力系數(shù)的估計值與測試值對比Fig.14 Comparison of estimated and test values of road resistance coefficient

由圖13和圖14可知， 本文提出的算法可以較為準確地對履帶車輛行駛過程中的道路阻力系數(shù)和轉向阻力系數(shù)進行估計。

5 結論

1) 以獨立電驅動履帶車輛的大量試驗數(shù)據(jù)為依托，通過路徑分割- 路徑段聚類- 建立運動基元的方式，實現(xiàn)了對行駛數(shù)據(jù)的統(tǒng)計學表述。

2) 利用運動基元的種類對行駛數(shù)據(jù)重新分組，建立了對應的驅動力統(tǒng)計學預測模型，可對兩側主動輪轉矩進行較準確的預測。

3) 驅動力統(tǒng)計學預測模型與車輛動力學模型相結合，對履帶車輛行駛過程中的道路阻力系數(shù)和轉向阻力系數(shù)進行了合理估計，其中轉向阻力系數(shù)的估計誤差低于10%，道路阻力系數(shù)的估計誤差低于15%。

本文對于履帶車輛的動力學研究具有一定參考意義，同時也可以進一步拓展到利用地面參量進行履帶車輛的軌跡預測或者局部路徑規(guī)劃方面。