離心鋼管混凝土長柱軸壓性能分析

曹玉娟，婁晨光，趙銳，戴良軍，陳剛

(1.合肥工業大學 土木與水利工程學院，安徽 合肥 230009；

2.安徽建工集團有限公司 安徽 合肥 230001)

0 引言

隨著我國裝配式建筑的不斷發展，離心鋼管混凝土結構作為一種新型的預制結構在工程上得到了廣泛的應用。離心鋼管混凝土長柱是在鋼管中泵入高強混凝土，經離心成型、蒸壓養護等工藝生產制成的新型組合結構[1-2]。構件受力時，外部的鋼管會對內部核心混凝土產生約束，阻礙內部混凝土進一步變形，而內部的混凝土亦能阻礙鋼管屈曲，使構件軸壓承載力得到提高。典型的離心鋼管混凝土柱截面如圖1所示。

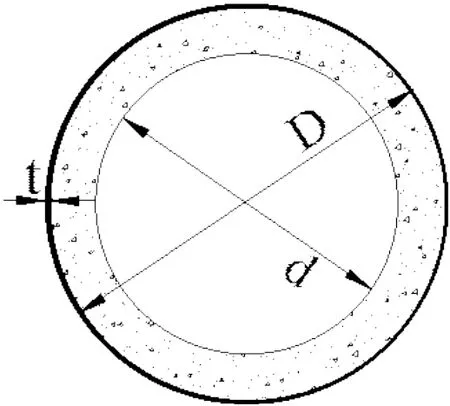
圖1 離心鋼管混凝土長柱截面

國內許多學者對離心鋼管混凝土柱的軸壓性能、抗彎性能及抗剪性能進行了試驗研究與有限元分析[3-8]，而對離心鋼管混凝土長柱軸壓承載力的研究仍較少，原因是軸壓試驗需要大噸位壓力機，實驗室條件有限，往往無法滿足。

運用ABAQUS有限元分析軟件，依據王宏偉、鐘善桐等對圓形空心鋼管混凝土長柱進行的軸壓試驗[9]，建立準確的有限元模型，試件的截面參數與材料參數見表1。在此基礎上采用正交試驗的設計方法[10]，討論鋼管壁厚、空心率、長細比對軸壓承載力的影響能力。將有限元計算結果與疊加理論和統一理論計算值進行比較，為離心鋼管混凝土長柱的工程運用選擇合適的計算理論。

表1 試件截面參數與材料參數

1 有限元模型建立

1.1 材料本構

為了驗證ABAQUS有限元模型的準確性，根據表1中的數據，結合下述五種不同本構模型，建立20個有限元模型。繪制長柱軸向荷載與跨中撓度的N-U關系曲線如下。

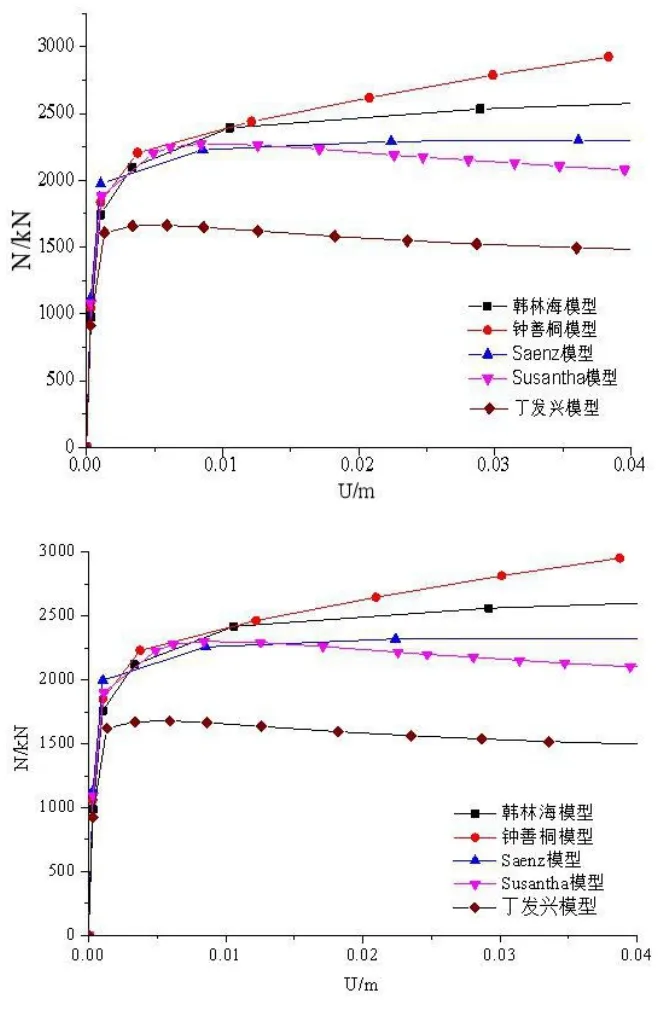
圖2 試件ZZ-1-1，ZZ-1-2的N-U關系曲線

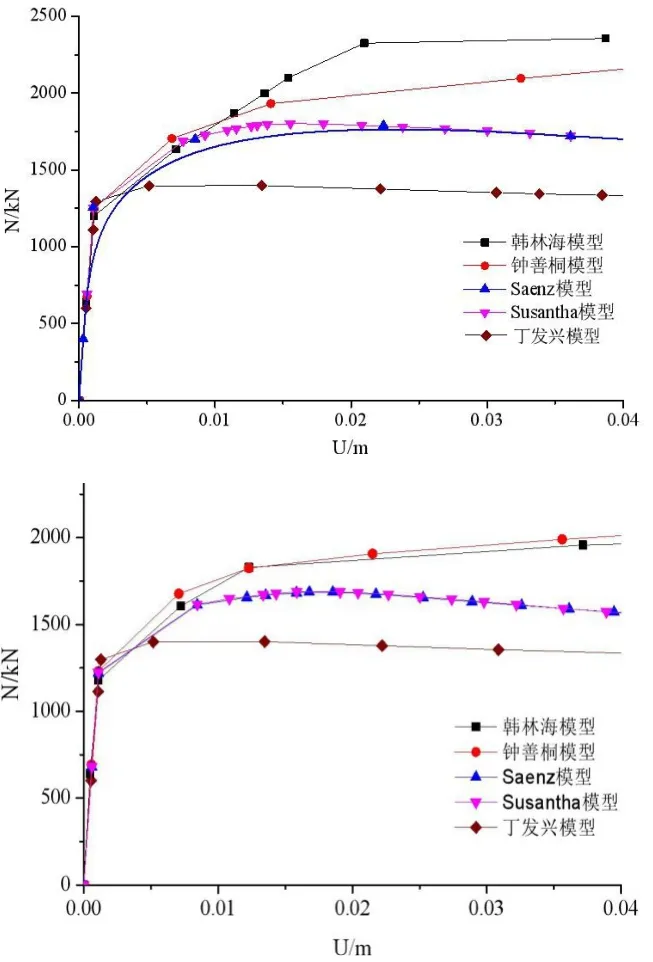
圖3 試件ZZ-2-1，ZZ-2-2的N-U關系曲線

由圖2、圖3可知，長柱軸心受壓時，構件到達材料彈性極限前，各本構關系模型的N-U曲線近似成一條直線且無太大差別；過了彈性極限后，五種本構關系變化顯著。鐘善桐本構模型與韓林海本構模型曲線在非彈性階段隨著跨中撓度的增大，構件承載力也不斷增加，但增加幅度不斷降低，且無下降段；Saenz本構模型隨著軸向變形不斷增加，有一段較明顯的下降段，而后曲線隨跨中變形的增大，N-U圖形近似呈一條直線；Susantha本構模型隨著跨中位移不斷在增大，在達到峰值承載力后，隨著跨中位移不斷增大，軸向承載力不斷降低，更符合試驗現象，且達到一定軸向變形后，其承載力逐漸保持穩定。丁發興模型在彈性階段，其承載力隨跨中撓度的增加而增加，到達峰值后，有明顯的下降段，但總體上其承載力數值小于其他四種本構模型。就試驗現象而言，丁發興模型與Susantha模型更為貼合，其下降段也更為明顯。

將有限元模型中導出的極限承載力數值與試驗實際承載力數值進行對比，得到表2。

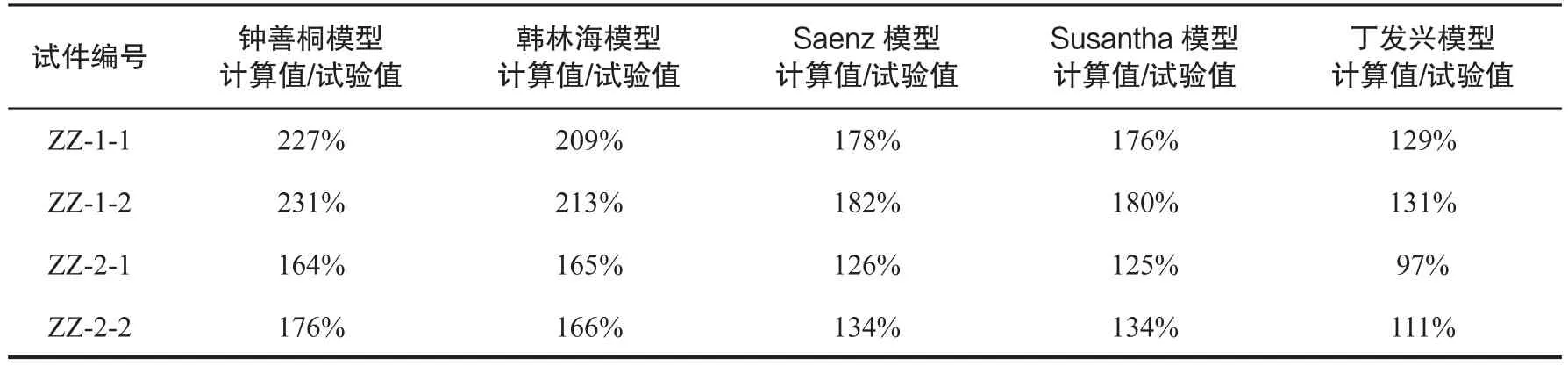
表2 構件各有限元計算值與試驗值差異百分比

從表2的數據可看出，鐘善桐模型與韓林海模型極限承載力與試驗值相差較大，數據過大，并不能準確反映軸壓構件的極限承載力。Saenz模型與Susantha模型與試驗值較接近，但二者極限承載力數值偏高。丁發興模型計算值數據與試驗值較吻合，較Susantha模型計算值低，數值偏為安全。因此，混凝土的本構模型選用丁發興本構模型[11]。

鋼材本構模型選用簡化的雙折線模型，同時，考慮到包辛格效應，在鋼材的塑性參數設置里選取隨動硬化作為塑性模型的硬化規律。

1.2 相互作用

考慮鋼管與混凝土之間的相互作用、構件與上下墊板之間約束。在interaction模塊中將鋼管與混凝土的接觸作用設置為“面對面接觸”，其接觸作用定義為兩個方向：1.接觸面間的法向作用，法向作用采用“硬接觸”；2.接觸面之間的切向作用定義為庫倫摩擦接觸，定義為“罰”，摩擦系數取0.3。鋼管表面與上下墊板表面定義為綁定(tie)接觸。

1.3 邊界條件

為與試驗邊界條件更加吻合，長柱下部墊板定義為完全固定，上部墊板定義為自由端；考慮到長柱本身會有初始缺陷，為了更加真實的反映長柱的受力狀態，采用施加千分之一柱長的初始偏心距來模擬其初始缺陷[12-13]。在加載線上施加Z方向的位移，同時約束上部墊板加載線X、Y方向的自由度，加載線布置如圖4所示。約束底部墊板X、Y、Z方向的自由度。

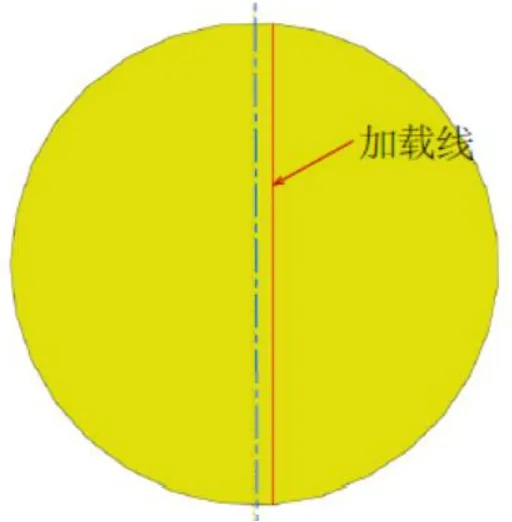
圖4 加載線的布置

1.4 網格劃分

在Mesh模塊中為各部件實例布置種子。鋼管與墊板均采用八節點非協調線性六面體單元(C3D8I)，混凝土采用八節點減縮積分線性六面體單元(C3D8R)并采用沙漏控制。同時考慮到有限元軟件計算的收斂性與計算的精度，合理劃分網格大小。離心鋼管混凝土長柱有限元模型如圖5所示。

圖5 有限元模型

2 正交試驗設計

在上述有限元建模方法的基礎上，考慮鋼管壁厚t、空心率ψ及長細比λ三種因素在不同水平下對離心鋼管混凝土長柱軸壓承載力的影響，選用正交表L9(34)對有限元模擬方案進行設計，各因素的不同水平取值如表3所示，按照表中的數據，需在ABAQUS有限元軟件中建立9個不同規格的模型，如表4所示。各試件均采用C40混凝土，即fck=26.8 MPa，鋼管采用 Q345，即 fy=345 MPa，試件外徑D為 400 mm，內徑d分別為 340 mm、320 mm、300 mm。試件截面如圖1所示：力-跨中位移曲線可近似分成三段：

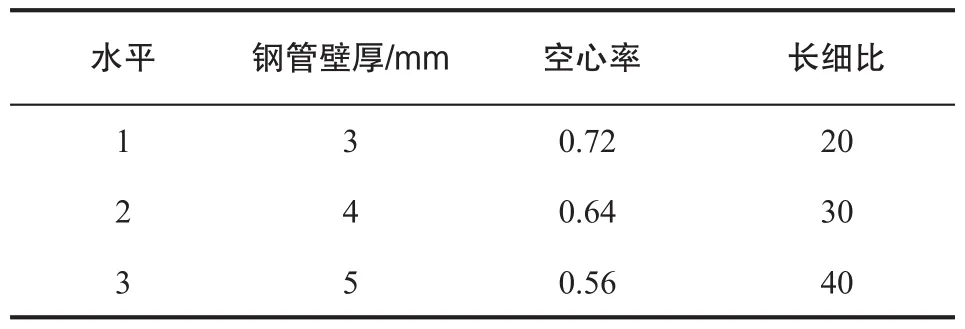
表3 因素水平表

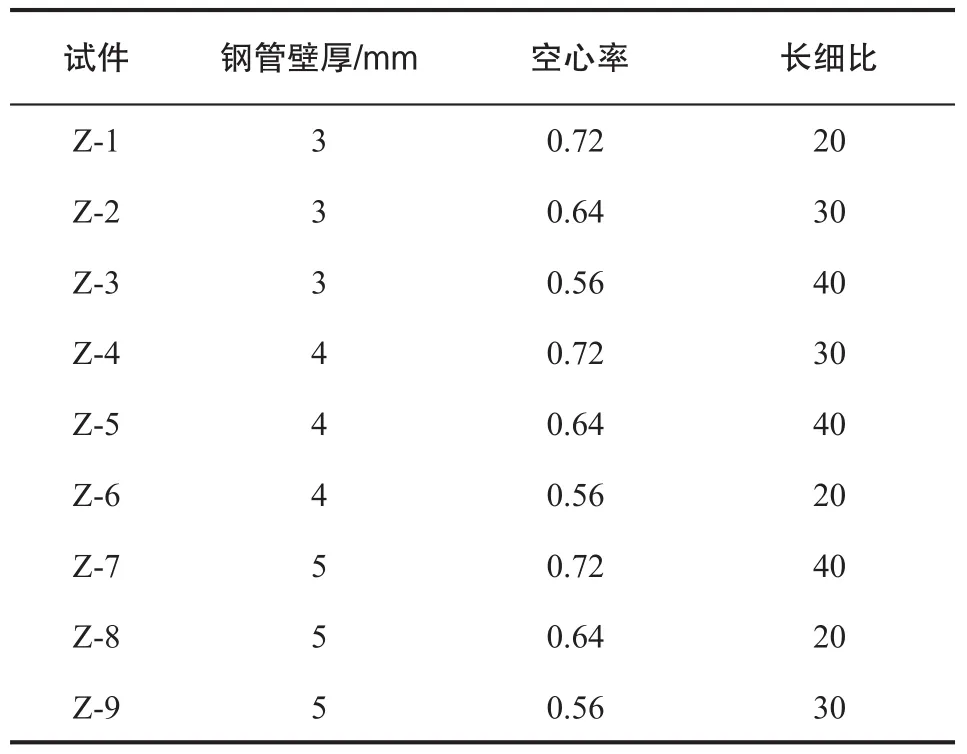
表4 正交分析模型規格

第一階段是加載初期的彈性階段。N-U關系曲線呈線性關系，此時鋼管和混凝土之間相互作用很小，可近似認為二者單獨受力，都處于彈性工作狀態；第二階段是屈服階段。隨著外荷載不斷增大，外部鋼管逐漸屈服，內部混凝土產生明顯的橫向變形。此階段鋼管開始對內部混凝土產生約束，因而內部混凝土強度得以提高，N-U曲線出現非線性增長，且增長的幅度逐漸減小；第三階段是破壞階段。長柱的軸壓承載力逐漸下降。隨著外荷載的進一步加大，跨中撓度不斷增加，對構件產生較大的附加彎矩，柱子開始失穩，因而曲線出現下降段。

3 有限元結果的正交分析

根據正交設計有限元模型分析的結果，繪制9組組合的軸向承載力與跨中位移圖(N-U圖)，如圖6所示：

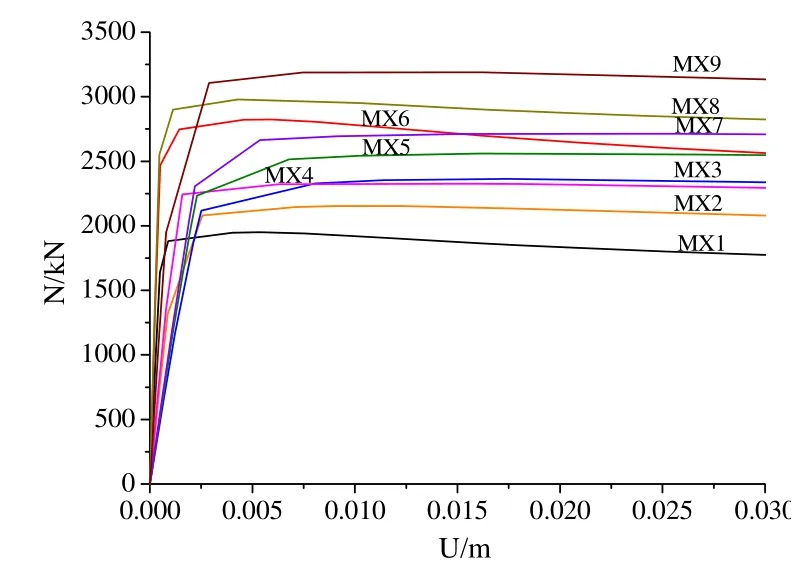
圖6 正交分析模型N-U曲線

由圖6可知，軸心受壓離心鋼管混凝土長柱軸提取各模型的軸壓極限承載力值繪制得表5。

表5 極限承載力

采用直觀分析法對本次模擬進行因素水平分析。通過比較各因素極差的大小來判定各因素的主次順序。分別將鋼管壁厚、長柱空心率及長柱長細比定義為因素A、因素B及因素C。對于每個因素，將處于同一水平的3個模型分為1組，對3組模型進行組間分析，得到該因素對分析指標的影響效應趨勢。根據表1、表2及表3中的數據，計算得極差分析表6。

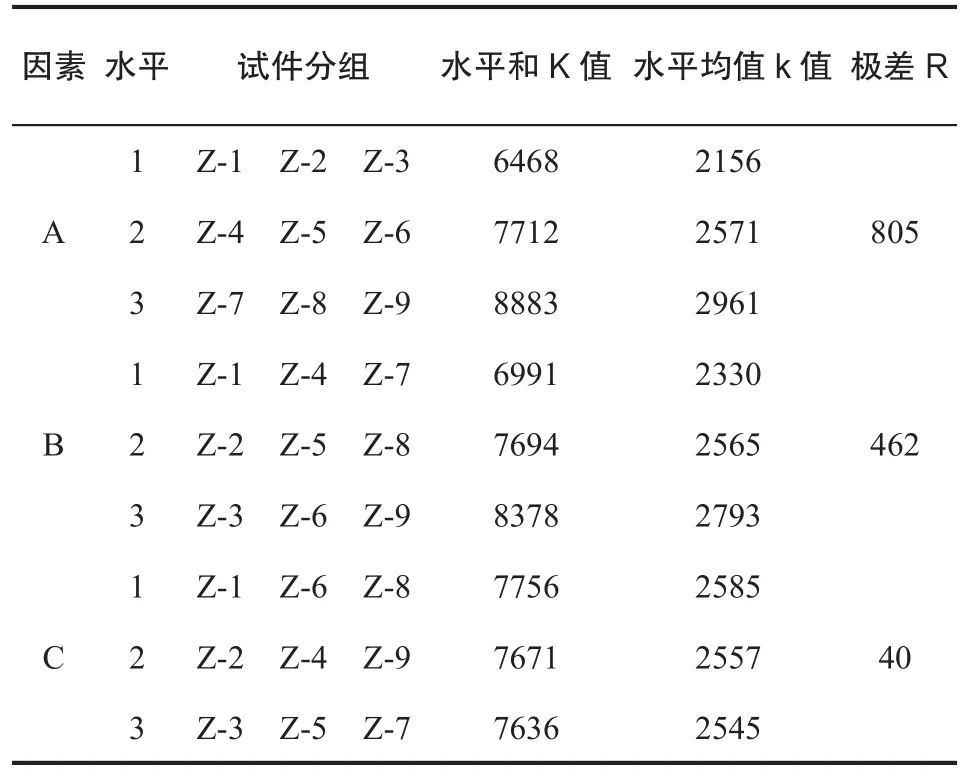
表6 極差分析計算表

利用表6中的數據，繪制鋼管壁厚、長柱空心率及長細比各因素對離心鋼管混凝土長柱軸向受壓極限承載力的影響圖。如圖7所示：

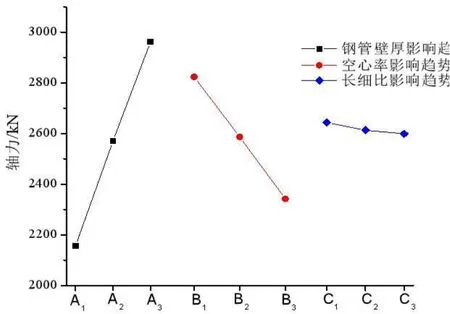
圖7 各因素影響趨勢圖

對于因素A，即鋼管壁厚t，長柱軸壓承載力與鋼管壁厚近似呈現線性正相關關系，鋼管壁厚每增加1 mm，其軸壓極限承載力增加約17%，且第三水平最優；對于因素B，即空心率ψ，軸壓承載力與空心率近似呈現線性負相關關系，空心率每增加0.08，其軸壓極限承載力減少約9%，且第三水平最優；對于因素C，即長細比λ，軸壓承載力與長細比無明顯線性相關關系，隨著長細比的增加，軸壓承載力逐漸降低，其承載力降低幅度均小于1%，可認為長細比對離心鋼管混凝土長柱軸壓承載力影響較小。

由表6中三種因素的極差值R可看出：RC＜RB＜RA。可知，上述因素中影響長柱軸向受壓承載力主要是鋼管壁厚，空心率次之，長細比對其影響最小。

綜上所述，考慮三種因素所有水平，上表中最優組合應選為 t=5 mm，ψ=0.56，λ=20。

4 長柱軸壓承載力理論計算

(1)疊加理論計算方法

薄壁離心鋼管混凝土結構技術規程[14]基于疊加理論對離心鋼管混凝土長柱軸壓承載力計算如下：

(2)統一理論計算方法

鋼管混凝土結構技術規范[15]基于統一理論對離心鋼管混凝土長柱軸壓承載力計算如下：

上式中，Nu為長柱軸壓極限承載力；N0為短柱軸壓極限承載力；?L為考慮長細比影響的承載力折減系數；?e為考慮長柱初始偏心影響的承載力折減系數；fsc為鋼管混凝土軸壓組合強度；Asc為鋼管混凝土橫截面面積；?sc為軸心受壓構件穩定系數。

使用上述公式計算所得承載力與有限元模擬結果對比見表5。

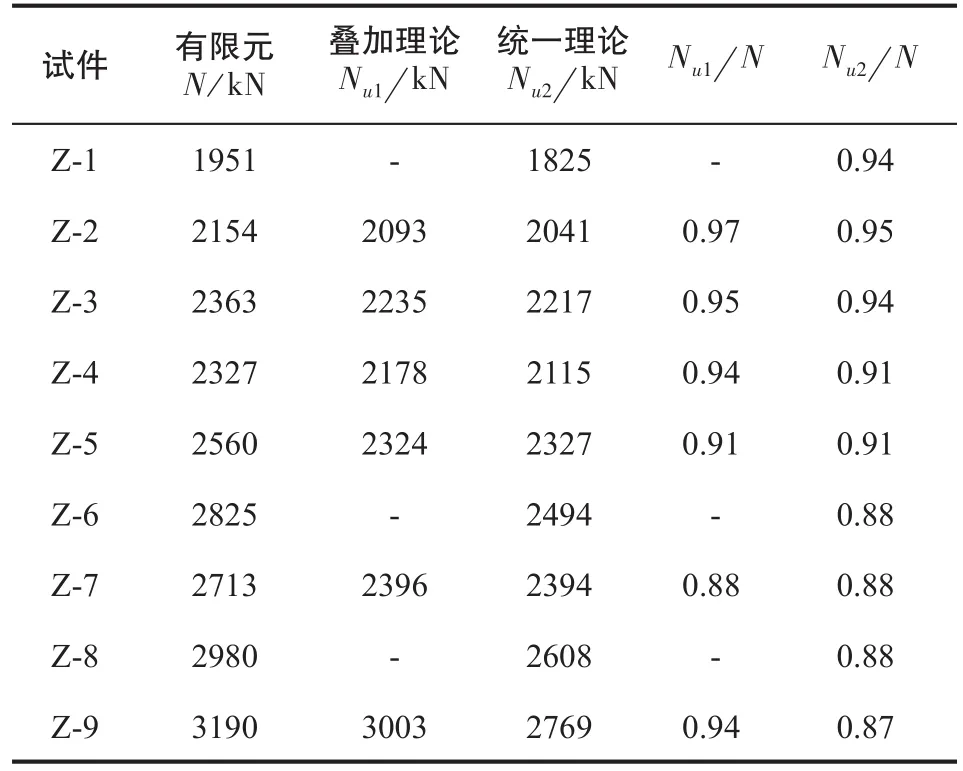
表5 有限元與理論計算結果對比

由表5可知，疊加理論與統一理論計算長柱軸壓承載力所得值較有限元模擬值均偏小。Nu1N的平均值為0.93，即理論計算值較有限元模擬值偏小7%，Nu1N計算方差為0.00081；統一理論計算長柱軸壓承載力所得值與有限元模擬值較吻合，Nu2N的平均值為0.91，即理論計算值較有限元模擬值偏小9%，Nu2N計算方差為0.00079。疊加理論計算公式(2)在考慮長細比影響的承載力折減系數?L時，對于長細比較小的試件無法計算，該公式的應用有局限性。而統一理論計算結果更偏于安全，進一步驗證了有限元模型的準確性，可知統一理論計算值與有限元模擬值吻合更好。

5 結論

(1)鋼管壁厚、空心率及長細比對離心鋼管混凝土長柱軸壓承載能力的影響能力順序依次為：鋼管壁厚＞空心率＞長細比。長柱軸壓承載力與鋼管壁厚近似呈現線性正相關關系，鋼管壁厚每增加1 mm，其軸壓極限承載力增加約17%；與空心率近似呈現線性負相關關系，空心率每增加0.08，其軸壓極限承載力減少約9%；與長細比無明顯線性相關關系，隨著長細比的增加，軸壓承載力逐漸降低，其承載力降低幅度均小于1%。

(2)疊加理論計算值比有限元模擬值小7%，其計算方差為0.00081，統一理論計算值比有限元模擬值小9%，其計算方差為0.00079。統一理論計算值與有限元模擬值吻合較好，工程上選用統一理論計算離心鋼管混凝土長柱軸壓承載力更偏于安全。

(3)采用丁發興混凝土本構模型進行離心鋼管混凝土長柱軸壓性能有限元分析，能較好的模擬其變形性能和承載能力。