傳動鏈動態誤差分析及不確定度評定

吳躍波，董海峰，程真英

(1.安徽建筑大學 機械與電氣工程學院，安徽 合肥 230601；

2.合肥工業大學 儀器科學與光電工程學院，安徽 合肥 230002)

0 引言

隨著測量技術的進步，現代測量技術的主流方向是動態測量技術。由于動態測量具有時變性、隨機性、相關性和動態性等基本特性[1]，動態測量數據已經不適合用傳統靜態誤差理論來分析和處理，并且動態誤差理論還處于研究起始階段。因此，為提高動態儀器設備的檢測與控制精度，需要進一步深入研究動態測量誤差的規律與特性。

傳動鏈結構在機械設備中非常常見，如減速器、一維平臺、聯軸器等。為實現對機械設備傳動精度的有效控制，有必要深入研究傳動鏈的動態誤差特性，對傳動鏈設備的進行針對性的改進和指導。目前針對傳動鏈動態誤差特性研究的思路主要有兩種：一是根據儀器設備的內部結構參數進行理論建模分析；二是對傳動鏈的誤差進行綜合檢測研究。對于前者，萬慶祝等根據薄殼彈性變形理論，通過分析諧波傳動工作原理，在回差和剛度條件下建立諧波齒輪減速器傳動誤差公式[2]；鄧效忠等通過齒面點旋轉的諧波運動軌跡，建立了齒輪傳動誤差的單面嚙合測量模型和齒輪傳動誤差的三種計算公式[3]；李兵等在研究RV減速器結合擺線針輪傳動機構多齒嚙合特性的基礎上，分析擺線輪自轉誤差，轉角誤差和建立傳動誤差分析模型[4]；這種方法從系統動態運動的機理上建模分析，模型精確，但要求建模人員詳細準確地掌握系統內部的結構參數和具有較高的專業能力，且建模過程復雜，實際應用困難。對于后者，陳青蘭等通過構建高速動態傳動誤差測試系統，測量某直齒輪-錐齒輪二級傳動系統的誤差曲線并加以頻譜分析，研究傳動系統的誤差特性[5]；劉洋等設計齒輪動態傳動誤差的測量系統，得到了動態誤差曲線，并對其進行頻譜分析[6]。這種方法則不需要已知系統內部的結構參數信息，只要通過對比傳動鏈的輸入輸出信號，即可檢測得到其綜合誤差特性。但研究的傳動鏈元件比較單一，針對齒輪、軸承的研究較多，如倪莊等針對軸承誤差測量，研制了基于電子技術的軸承在線檢測系統[7]。而對其他傳動鏈元件研究較少，而且沒有對檢測出來的動態誤差進行不確定度評定，檢測結果的可靠性難以保證。

本文基于綜合測量系統整體誤差的思路，對常見的由減速器、聯軸器、位移平臺組成的傳動鏈結構，設計了一套傳動鏈動態誤差分離實驗系統。通過傳動鏈的輸入輸出信號的測量比對，得到傳動鏈系統的動態誤差曲線，為傳動鏈誤差的后續分析、誤差溯源、優化改進設計提供參考。同時為保證動態誤差檢測結果的精度與可靠性，對實時分離的動態誤差進行了不確定度評定。

1 傳動鏈動態誤差分離實驗系統工作原理

本文通過傳動鏈系統和信號采集系統建立傳動鏈動態誤差分離試驗系統。傳動鏈系統包括：伺服電機、減速器、一維位移平臺以及聯軸器。其中減速器由伺服電機驅動，減速器內部減速后，其輸出軸通過聯軸器控制一維位移平臺的移動。信號采集控制系統包括長光柵、伺服電機內置編碼器和運動控制卡。長光柵安裝在一維位移平臺，主要測量一維位移平臺的移動距離，伺服電機內置編碼器反饋電機轉動角度。信號采集控制系統以伺服電機內置編碼器反饋脈沖為標準量，以長光柵輸出脈沖為比較量，同步采集兩者的脈沖增長，并進行比對，經過LabVIEW程序處理之后，即可獲得傳動鏈系統動態誤差的分離值。系統的運動控制卡一方面用于控制伺服電機的正常運轉和參數設置，另一方面實現伺服電機編碼器和長光柵脈沖的同步采集。實驗系統的設計思路如下圖1所示：

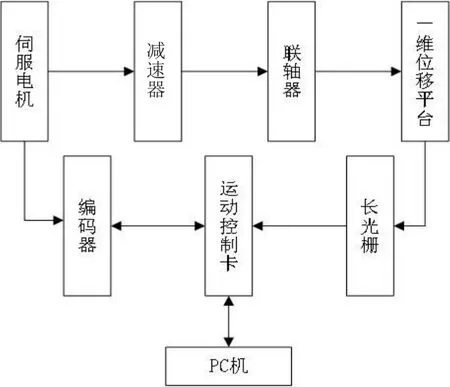
圖1 傳動鏈動態誤差分離實驗系統原理圖

減速器

假設伺服電機的轉動角度設為θ1，減速器減速比設為i，一維位移平臺滾柱絲杠導程為S，一維位移平臺在移動的理論距離為L：

θ

1

由伺服電機編碼器反饋脈沖測得：

式(2)中，N1—伺服電機反饋脈沖量，λ1—伺服電機電機轉動一圈反饋脈沖量，設置為36000。

受動態傳動過程中聯軸器、減速器以及一維位移平臺各環節傳動鏈誤差的影響，長光柵檢測到的平臺實際距離L1與理論距離L不同，傳動鏈動態誤差ΔL計算式為：式(3)、式(4)中，L1—位移平臺實際移動距離，N2—長光柵輸出脈沖，σ—長光柵分辨率。

1.1 系統硬件設計

實驗系統中選用日本Panasonic公司A4系列伺服電機，該電機具有高性能CPU，1KHZ的速度響應頻率和自動調諧功能，保證電機在運轉過程中的速度穩定和方向調節，它由伺服驅動器MAD‐DTl205和電機MSMD012S11兩部分組成。減速器傳動比為20。一維位移平臺采用北京光學儀器廠MTS103電控平移臺，該位移平臺的絲桿導程4 mm，最大行程距離為150 mm。聯軸器為波紋管聯軸器。長光柵兩端固定在一維位移平臺側面，選用貴陽新天公司JCXE0.2光柵尺，分辨率0.2 um，有效行程距離為150 mm。整體結構如圖2所示：

圖2 實驗系統結構圖

1.2 電機控制與信號采集系統設計

系統中驅動電機的控制與傳感器信號的采集主要通過眾為興公司ADT-8940A1四軸運動控制卡來實現，該控制卡是基于PCI總線的高性能四軸控制卡，自帶采集功能，且采集頻率最高為2 M，計數器高達32位，能夠滿足對電機的穩定控制和脈沖信號采集同步的要求。系統電機控制與脈沖采集的電氣接線如下圖3、下圖4所示。

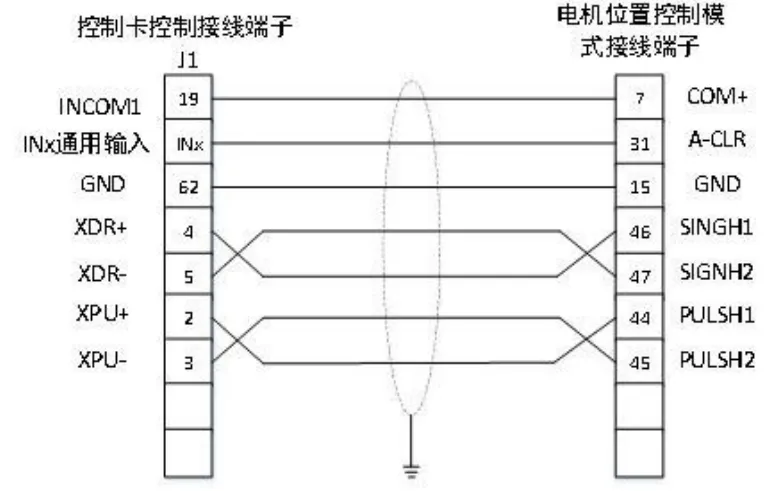
圖3 伺服電機電氣接線圖

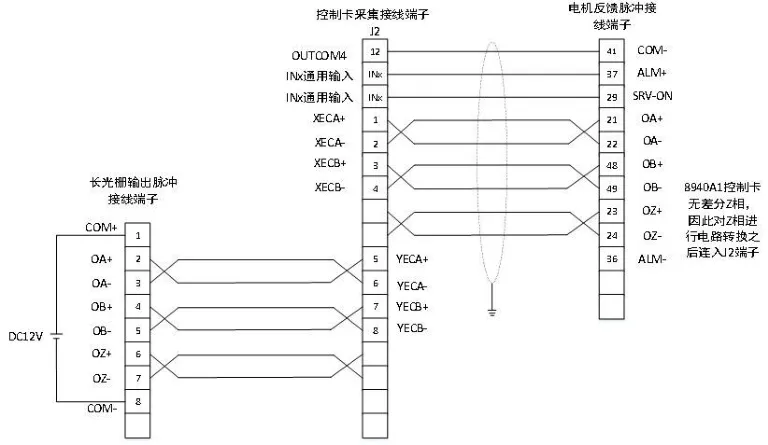
圖4 脈沖采集電氣接線圖

伺服電機工作模式設置為位置控制模式，通過外部脈沖信號控制電機的速度和轉動時間。電機的輸入脈沖引腳為PLUSI(45腳)和方向信號SIGN1(47腳)。反饋脈沖引腳分別為21腳、22腳(輸出A向脈沖)和48腳、49腳(輸出B向脈沖)，由于系統中伺服電機內置17位編碼器，使得運動控制卡驅動電機所需指令脈沖和表示電機轉動圈數的反饋脈沖的目太大，不利于運動控制卡對電機控制和電機脈沖采集。因此通過伺服電機的電子齒輪功能對指令脈沖和反饋脈沖進行分倍頻設置，使得電機及其脈沖更易被控制和采集。

1.指令脈沖分倍頻設置：

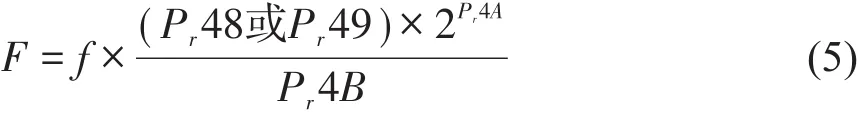
式(5)中，F為編碼器分辨率；f為指令脈沖頻率；設置電機指令參數Pr48=1，Pr49=1，Pr4A=17，Pr48=5000。則f=5000，即電機每轉1圈需要5000個脈沖。

2.反饋脈沖分倍頻設置：伺服電機處于位置控制模式下，設置Pr45=0，每轉反饋脈沖數P脈沖數=Pr44×4，為了數據處理的方便，設置Pr44=9000，即伺服電機每轉一圈的反饋脈沖數為36000。

1.3 基于LabVIEW信號采集與控制程序

傳動鏈動態誤差分離系統的軟件部分是使用NI公司的圖形化編程語言LabVIEW所編寫，以程序結構模塊化方法設計了檢測與控制系統，主要功能有電機運動控制、脈沖信號采集、傳動鏈系統動態誤差數據處理。系統程序流程圖為下圖5所示：

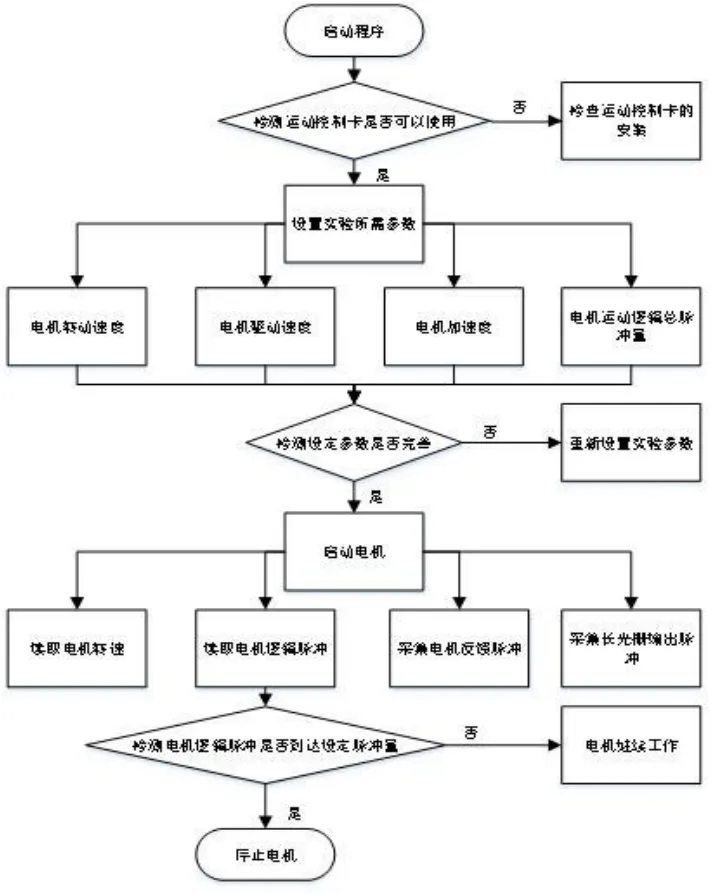
圖5 傳動鏈動態誤差分離系統脈沖采集與電機控制系統流程圖

圖6 為實驗系統脈沖采集與電機控制程序界面，主要包括對電機參數的設置、電機反饋脈沖數和長光柵脈沖數的讀取以及系統動態位移誤差的分離。其中脈沖數和位移誤差的采集通過波形圖顯示，具體數據可以從波形圖設置中導出。

圖6 實驗系統脈沖采集與電機控制程序界面

2 傳動鏈動態誤差分離系統的不確定度評定

2.1 誤差來源分析與建模

實驗系統得到的傳動鏈動態誤差分離數據是由同步采集的電機內置的高精度編碼器和長光柵測量數據比對得到的。經分析，測量數據的不確定度不僅與系統中涉及的電機、長光柵自身參數誤差有關，還與采集的同步性、多次檢測的重復性以及長光柵安裝的阿貝誤差密切相關。由于運動控制卡計數輸入通道相互獨立，全部光耦隔離，通道同步時間間隔較短，脈沖采集速度低等原因，因此運動控制卡引入的采集同步性誤差可以忽略不計。通過系統構建的傳動鏈動態傳動誤差測量的數學公式，建立系統的誤差模型為：

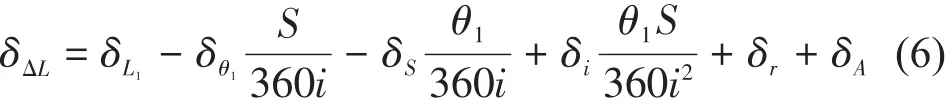
式(6)中，δΔL—傳動鏈動態誤差，δL1—長光柵誤差，δθ1—伺服電機編碼器角度誤差—伺服電機編碼器角度誤差傳遞系數，δS—一維平臺導程誤差—一維平臺導程誤差傳遞系數，δi—二級斜齒輪減速器減速比誤差，—二級斜齒輪減速器減速比誤差傳遞系數，δr—測量重復性誤差，δA—阿貝誤差，S—位移平臺導程，i—減速器減速比。

因此，通過測試數據或相關資料評定出各來源的不確定度分量，合成實驗系統總誤差分離結果不確定度。

2.2 A類不確定度評定

在本次測試中，伺服電機的速度為30 r/min，重復測量10次，并且對數據進行處理得到10組動態誤差曲線(見圖7)，由此對系統重復實驗引起的不確定度進行評定。

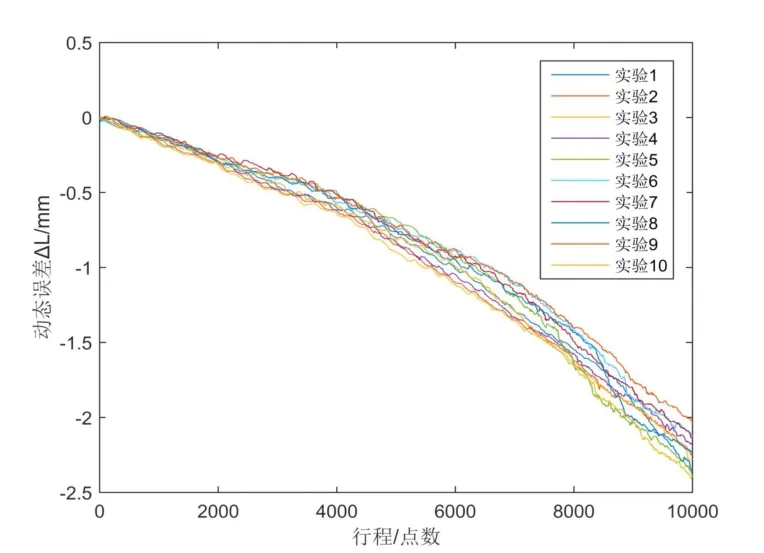
圖7 重復實驗動態誤差曲線

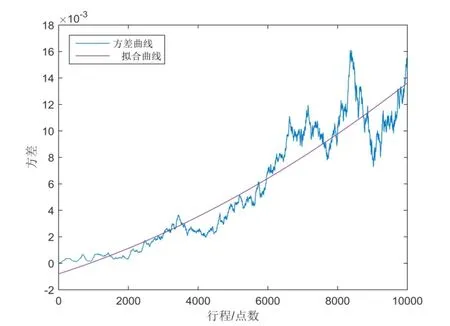
圖8 方差曲線

首先根據圖7所示的動態傳動誤差數據，計算得到各個時刻點的方差，如圖8所示。從圖7、圖8中可以看出，動態傳動誤差數據是一個非平穩隨機過程，方差會隨著測量位移的增長而增大。為評定該項誤差引起的不確定度，有必要將方差曲線的趨勢項及其殘余項合成得到綜合的方差變化范圍，然后對其開根號得到其標準不確定度。

方差曲線的趨勢項可由通過二次多項式進行擬合，如式(7)。

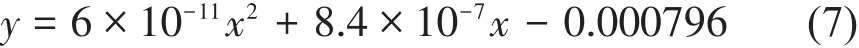
式(7)中，x—位移平臺移動行程，通過x測出位移平臺的運動距離。

方差曲線的殘余項可由殘差模量計算得到：

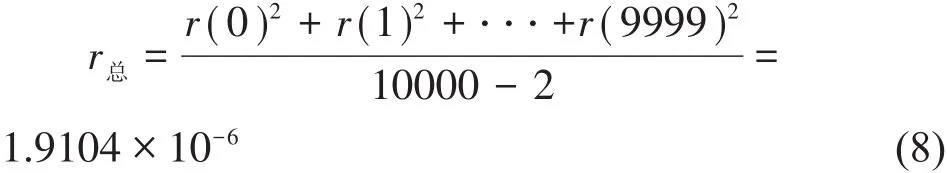
式(8)中，r(0)、r(1)、r(9999)—擬合曲線與實際曲線點的殘差量。

因此此項的標準不確定度u1為：

2.3 B類不確定度評定

2.3.1 長光柵誤差引起的不確定度分量

根據長光柵JXCE0.2的說明書，該長光柵的位移測量精度為±5 um，假定為均勻分布，傳遞系數為kL1=1，則該項不確定度u2：

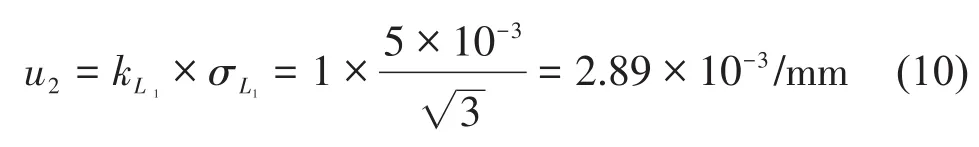
2.3.2 伺服電機編碼器角度誤差引入的不確定度分量

為了系統采集和處理數據的便利，根據松下A4伺服電機說明書，設置伺服電機轉動一圈的反饋脈沖量是36000，則伺服電機轉動角度的精度為0.01度。假定為均勻分布，傳遞系數kθ1=，則伺服電機編碼器角度誤差引入的標準不確定度u3：

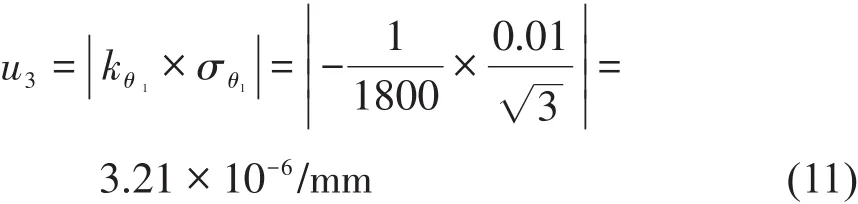
2.3.3 位移平臺導程精度引起的不確定度分量

根據一維位移平臺MTS103說明書可知，其導程的定位精度為0.005mm。假定為均勻分布，傳遞系數kS=-θ1，則該項不確定度分量u4：2.3.4 減速器減速比誤差引起的不確定度分量

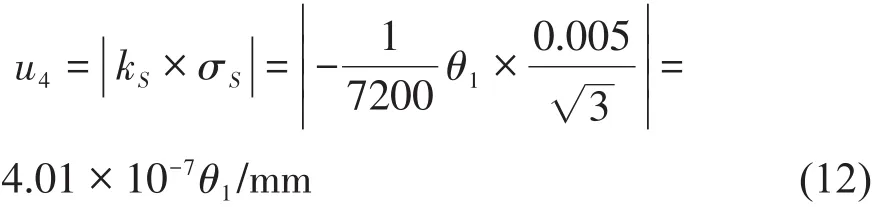
2.3.4 減速器減速比誤差引起的不確定度分量

系統中二級斜齒輪減速器的減速比在實驗過程中呈波動狀態，根據文獻[8]對該減速器研究發現，減速比的偏差范圍±0.0115，按均勻分布，傳遞系數ki=，則減速器減速比誤差引起的標準不確定度分量u5：

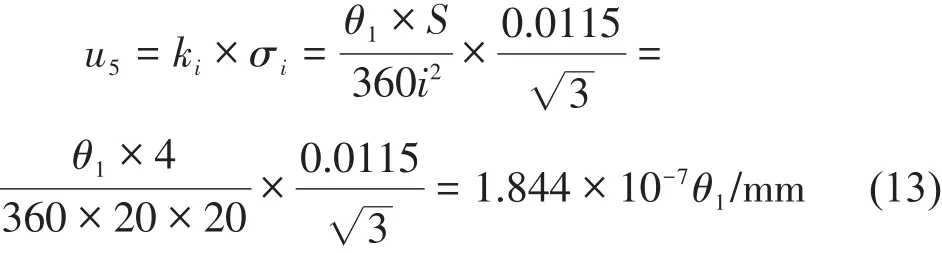
式(12)、式(13)中θ1的值可由位移平臺的移動距離求得：

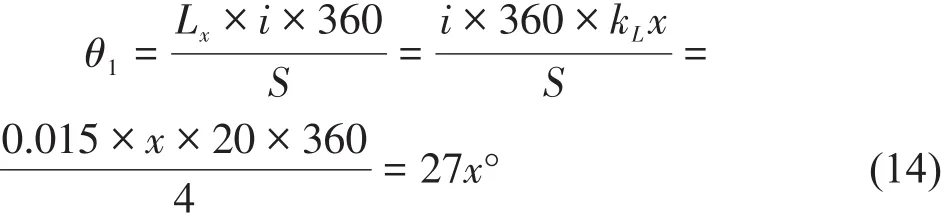
式(14)中，x—位移平臺的行程點數，kL—位移平臺移動距離Lx與行程點數x之間的系數，kL=0.015。

2.3.5 長光柵安裝誤差導致的不確定度分量

長光柵安裝在一維位移平臺側面，其移動光柵安裝在位移平臺的滑塊上。長光柵在安裝中與位移平臺會存在一定角度的偏移，使得滑塊在運動時，標準光柵尺與指示光柵之間的間隙發生變化，導致阿貝誤差的產生[9]。根據長光柵安裝說明可知，其安裝在一維位移平臺的平行度必須小于0.1 mm/1000 mm。則阿貝誤差為：

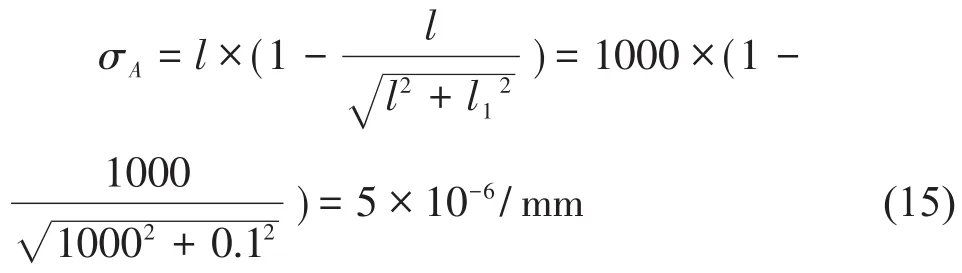
式(15)中，l—長光柵平行度標準測量距離，l1—長光柵平行度偏移距離

按均勻分布，其標準不確定度為u6：

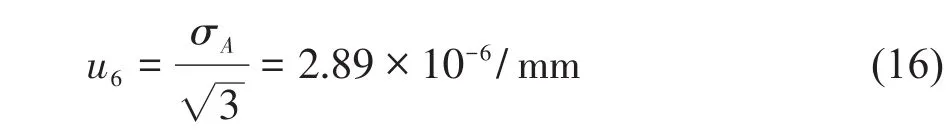
2.4 合成不確定度計算與分析

通過分析可知，上述各不確定度分量彼此相互獨立且互不相關，因此ρ=0。因此合成標準不確定度為：

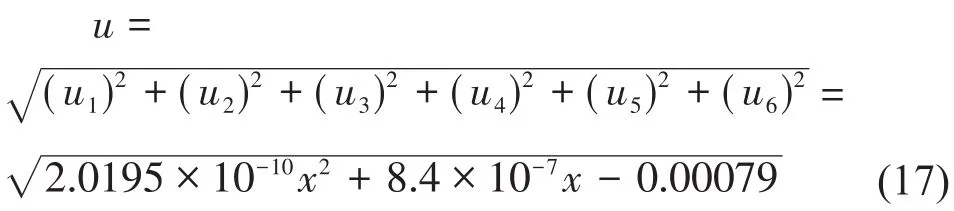
取包含因子k=0，則傳動鏈動態誤差分離系統的擴展不確定度為：

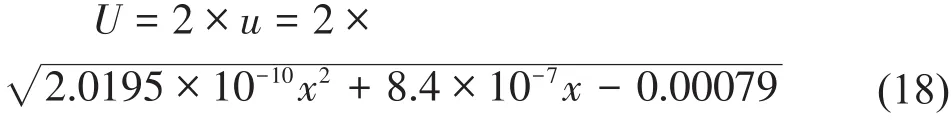
式(17)中，U隨著位移平臺移動距離的增長而增長。因此，當位移平臺的移動距離最大為150 mm 時，即 x=10000，Umax=0.33 mm，經計算滿足實驗要求。

3 傳動鏈動態誤差的測試結果

在上述研制的實驗系統上，進行了不同速度情況下的測試，得到了其傳動鏈動態誤差的測量結果數據，如圖9，圖10所示。

圖9(a)為電機轉速30 r/min時，傳動鏈動態誤差隨位移的變化情況。從整體上看，動態誤差的增長呈非線性，且增長過程中具有階段性和波動性。這主要是由于傳動鏈系統累積誤差不穩定原因導致的。在初始階段，誤差數據存在明顯跳變，經分析是因為傳動鏈結構的滯后性使得位移平臺移動滯后于電機運動，因此，在實際分析動態誤差時，要依據位移平臺和電機相差的滯后性時間刪去滯后性數據。對不同速度的數據同樣存在這一問題，按照相同的辦法修正。對圖9(a)中橢圓型區域進行細節展開，得到圖9(b)，在行程點0-150的距離中，動態誤差在1.275 mm處上下波動，在行程點150-350的距離中，動態誤差呈線性增長。通過頻譜分析，可以分析系統的動態誤差的頻率組成，為后期系統的動態誤差分解和溯源奠定了基礎。

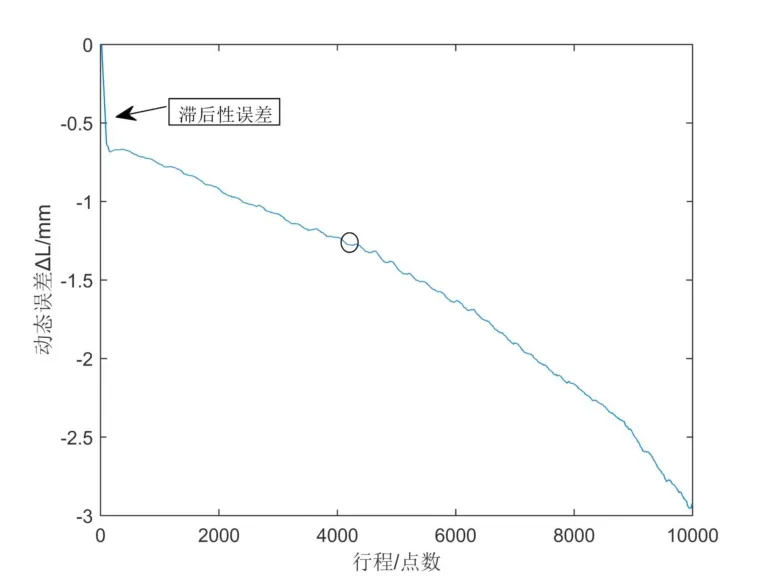
圖9 (a)30r/min下傳動鏈動態誤差

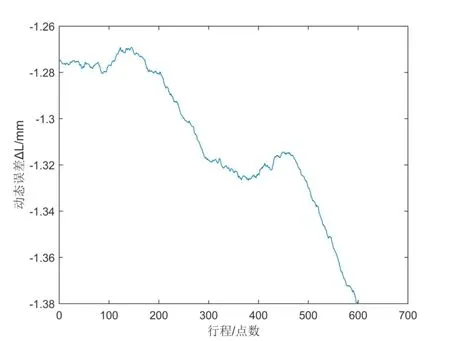
圖9 (b) 橢圓形區域動態誤差

圖10 所示是伺服電機轉速在30 r/min、40 r/min、50 r/min、60 r/min、70 r/min、80 r/min 和 90 r/min下系統動態誤差增長隨著距離的變化曲線。圖10(b)是圖10(a)中行程在行程點3000、4000和5000不同速度下的動態誤差，其中橫坐標表示電機的轉速30～90 r/min。圖10(b)中可以看出，傳動鏈系統的動態誤差隨電機轉速的增加而變大，表明電機速度對傳動鏈動態誤差具有一定程度的影響，因此在后期對傳動鏈動態誤差分解和溯源時，必須考慮速度的因素。

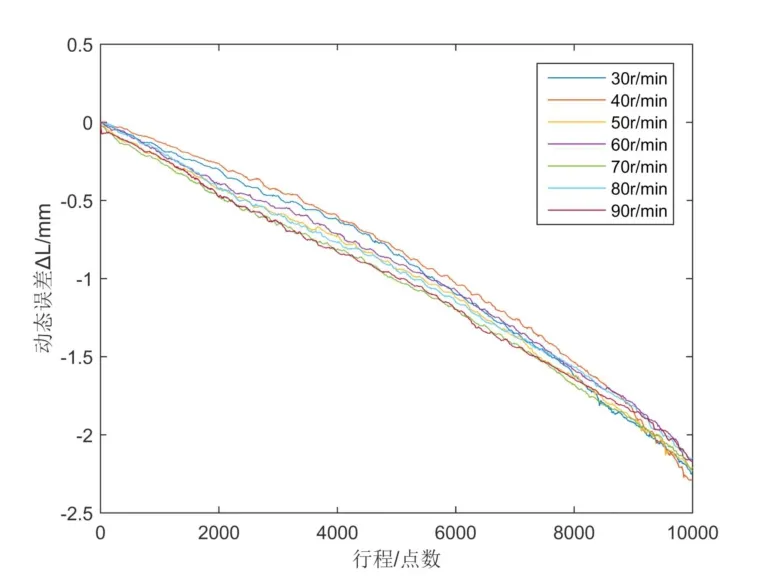
圖10 (a) 30～90 r/min下傳動鏈動態誤差曲線

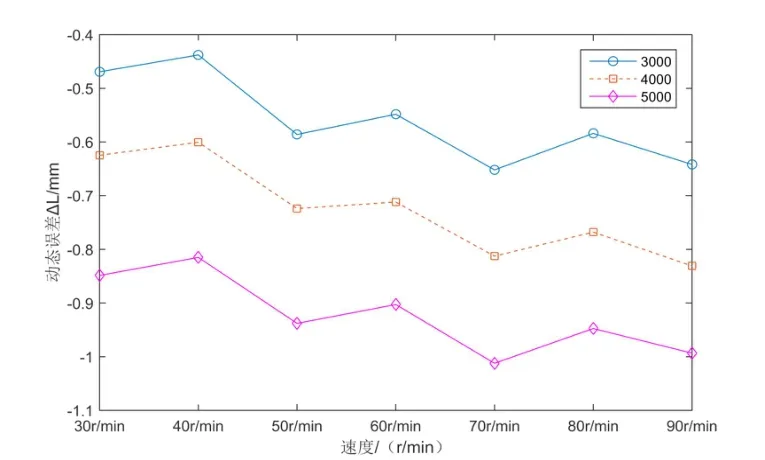
圖10(b) 同一行程點，不同速度下傳動鏈動態誤差

4 結論

本文根據動態誤差理論和系統整體誤差綜合測量思路，通過減速器、聯軸器、位移平臺組成的傳動鏈機構和伺服電機、長光柵、運動控制卡組成控制檢測機構，設計了一種傳動鏈誤差分離實驗系統，該系統能夠測量傳動鏈動態誤差的變化情況。同時，為了保證系統的精度，對系統進行了不確定度評定。經計算，該系統的擴展不確定度，滿足系統進行實驗的要求。當需要評定不同速度下的系統不確定度時，只需要通過上述不確定度的評定步驟進行即可。傳動鏈動態誤差分離系統的建立，為后期傳動鏈系統的誤差溯源、誤差分解和優化改進等研究奠定了基礎。