溝通內在聯系突出數學本質
——以《認識整百整千數》為例
包利華
數概念的教學在小學大致分為四個階段:20以內數的認識、100以內數的認識、萬以內數的認識、大數的認識。“萬以內數的認識”是認數的第三階段,與前兩個階段“20以內數的認識”和“100以內數的認識”相比主要教學內容相同,包括數數、數的組成、讀寫、比較大小等,都突出了對“計數單位”的認識;所不同的是,“20以內數的認識”側重認識計數符號,“100以內數的認識”側重認識位值,“萬以內數的認識”側重深入理解“十進制”和“位值制”。小學生對數概念的理解本質上是數學意義的理解。劉加霞教授指出:數概念的數學意義主要是指“數”是由不同計數單位及其個數相乘再累加構成的,其背后滲透的是十進制和位值制。從百以內到萬以內,隨著數位的擴展,計數單位的新增,數的結構和構成是一致的,每一個數位上的數都是若干個計數單位累加的結果。例如:4241是由4個千、2個百、4個十和1個一組成的,也可以寫成4000+200+40+1=4241。如何在數概念教學中幫助學生深入理解數學意義呢?筆者設計了《認識整百整千數》這節課,通過不同計數單位的累加得到整百數、整千數,進而溝通它們的內在聯系,突出數學本質。
一、目標定位深入本質
1.從學生的角度看,學生更愿意思考什么問題?
我們常說,學生會的不用教,學生學了還是不會的也不用教。就這節課而言,什么是學生會的?課前,筆者讓學生介紹自己喜歡的數,從中看出,經過“20以內數的認識”和“100以內數的認識”兩個階段的學習,學生對認數、數數、數的意義、讀法和寫法沒有困難,還能用畫圖和文字的方式來表征。那么,學生更愿意思考什么問題?學生愿意思考的應該是具有一定挑戰性的問題,也就是“跳一跳能夠摘到的桃子”。這節課的主要挑戰性問題有兩個:一是1000是怎么得出來的?二是如何溝通不同計數單位累加得到整百整千數?
2.從數學的本質看,展開什么樣的過程更有意義?
1000是怎么來的呢?從本質上看,1000的產生是基于三位數的認識,三位數能表示的最大數是999,要表示比999更大的數怎么辦?只能擴展數位。怎么表示?計數器上通過撥一撥擴展到千位,千位上撥一個珠子,代表1個千,因此有了四位數。也就是說,1000應該是999+1得到的。這個過程的展開,學生經歷了1000的再創造過程,體會到數位擴展的重要性,學會像數學家一樣思考問題。
據此,筆者把這節課的教學目標定位為兩個點:
(1)通過畫一畫、撥一撥、想一想等活動,把認數與計算相結合,讓學生經歷1000產生的過程,理解1000的來歷。
(2)通過溝通計數單位的內在聯系,讓學生掌握相同的數學結構,能利用相同結構順利認識更大的數。
二、學習材料具有結構性
教學片斷一:復習回顧整十數,認識整百數。
出示:

師:這是一個正方形,把它平分成10個小長方形。如果1個小長方形代表1,這個大正方形我們記做?
生:10。
師:是的,10個一是10。乘法算式是?
生:10×1=10。
(出示4張這樣的正方形圖)
師:現在記做?你是怎么思考的?
生:我是數的:1個十、2個十、3個十、4個十,4個十是 40。
生:我列乘法算式:10×4=40。(板書:10×4=40)
師:同學們用數和計算的方法得到了40。
出示:

師:現在我們把這個正方形再次平分,如果1個小正方形代表1,現在記做?
生:100。10個十是100。
生:一行有10個,有10行,所以是 10×10=100。
(出示4張這樣的正方形圖)
師:可以怎么表示?
生:400。100×4=400,4 個百是 400。(板書:100×4=400)
師:如果再增加1張呢?
生:500。100×5=500,5 個百是500。
師:還有不一樣的表達嗎?
生:10×10×5=500。
生:250×2=500。
生:400+100=500。
師:你知道他是怎樣想的嗎?
生:(指著黑板上5張正方形圖)原來有4個百,又增加1個百,就是5個百。
(繼續增加4張同樣的正方形圖)
師:你能像上面一樣,用多種方法得出900嗎?
生:100×9=900,9 個百就是900。
生:500+400=900。表示原來的500加上現在的400,共900。
生:300×3=900。
生:450×2=900。
生:400×2+100=900。
師:這道算式這么復雜,誰看明白了?
生:(指著圖形說)這里是2個400,再加上100。
學習材料的設計要有結構性,讓計算更具聯系性。在回顧整十數和認識整百數時,我以正方形為學習材料,注重溝通本質的聯系。100個、100個往上加得到整百數,在4張正方形圖的基礎上增加1張正方形圖,學生得到了400+100=500。這個過程喚起了學生對計數單位“一(個)”“十”“百”之間關系的回憶,然后主動將4個百加1個百等于500類比到4個十加1個十等于50或者是4個一加1個一等于5,學生在遷移、類比中找到了“4個計數單位加1個計數單位等于5個計數單位”這個本質結構。正是溝通了內在的聯系,學生容易抓住數概念的本質,也使得已有的學習經驗能夠迅速遷移到新知的理解當中來,在教師呈現900這個數的時候,學生就有了多樣的表征方式。
三、過程展開充分到位
教學片斷二:認識1000。
環節一:畫一畫。
師:900,好大一個數!如果再大一點你還會數嗎?
(在900的基礎上再10個、10個出示。學生10個、10個數到990;
在990的基礎上再1個、1個出示。學生1個、1個數到999)
師:我們剛才通過100個、100個,10個、10個,1個、1個地數得到了999,如果在999的基礎上再添上1是?
生:1000。
師:你們都知道是1000,那1000是怎么得出來的呢?
師:老師給你提供了這樣一幅計數器的圖,請你思考999+1怎么在計數器上表示呢?
出示:
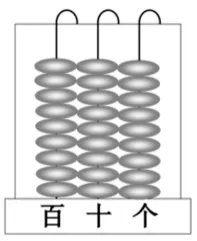
(反饋交流:同時出示三種典型的表示方法)
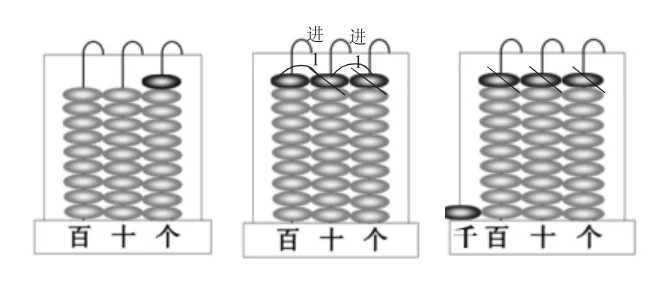
師:仔細觀察,靜靜地思考。你看懂了哪幾種表示方法?誰能來解釋?
生:第一種只是在個位加1。
生:第二種是個位加1,個位滿十向十位進一,劃掉,十位滿十向百位進一,劃掉,百位滿十向千位進一,劃掉。但是千位沒有畫出來。
生:第三種和第二種是一樣的,但多了千位。
師:比較三種不同的表示方法,你有什么想說的?
生:三種方法表示的過程是一樣的,但形式上不同,第三種增加了千位,更加清楚,我比較喜歡第三種表示方法。
師:是的,三個數位能表示的最大三位數是999,再添一個數不夠了,所以增加一個數位,叫做千位。
環節二:撥一撥。
師:剛才我們通過畫一畫表示了999+1。下面我們在計數器上撥一撥。同桌合作,邊撥邊思考:1.每次進的1表示什么?2.每次進1后得到哪些算式?
(反饋交流:學生演示)
生:999+1=1000。這個1表示1個一,算式是999+1。個位滿十向十位進一,這個1表示1個十,算式是990+10。
師:不好意思打斷一下,他說990+10誰看懂了?
生:我們看到的是990,還有1個十在他手里,還沒放下去。
師:謝謝你的慢鏡頭,讓我們清楚地看到了990+10這個算式。繼續。
生:十位滿十向百位進一,這個1表示1個百,算式是900+100。百位滿十向千位進一,這個1表示1個千。
師:同學們真會思考,我們終于得到了1000。誰把它寫出來?
生:寫作:1000,讀作:一千。
環節三:說一說。
師:認識了1000這個數,誰來介紹一下這個新的數?
生:1000是由 999+1得到的。
生 :999+1=1000,990+10=1000,900+100=1000。
生:10個百是 1000。100×10=1000。
生 :500 ×2=1000,200 ×5=1000,250×4=1000。
……
學生從999數到1000沒有困難,但為什么要有1000這個數,它是怎么得來的?這對學生來說是有挑戰性的問題。一方面,學生數概念擴展的經驗不足;另一方面,學生習慣于思考“是什么”的問題,對于“為什么”的問題思維經驗比較弱。因此,認識1000這個數,我設計了“畫一畫”“撥一撥”“說一說”三個環節,讓學生經歷1000的再創造過程。在此過程中,我給予學生足夠的思考空間,主要體現在集中反饋和問題設計上。學生畫完后,我把出現的三種典型作品集中呈現,并提出問題:“仔細觀察,靜靜地思考。你看懂了哪幾種表示方法?誰能來解釋?”學生的交流不拘一格,有的選擇一幅作品發表想法,有的選擇全部一一點評,還有的聚焦到兩幅作品進行對比溝通。這樣的反饋方式,再加上合理的問題設計,能有效幫助學生拓開思考的維度。最后是給予學生思考的時間,課堂時間有限,但是學生獨立思考的時間必須要有,靜能生慧,沒有獨立思考,憑什么交流?數學特級教師俞正強老師說:“人類的活動都有其特定的節奏,思維活動更是如此,有時頓悟,有時冥想。節奏是時間占有的藝術。”一節課短短40分鐘,筆者在“認識1000”這個環節花了20分鐘。這20分鐘里,學生在“畫”前思考、在“撥”時思考、在“說”前又思考,通過思考、交流、再思考、再交流,最后學生在介紹1000這個數時,表達十分豐富。正是因為給予了充分的信任和足夠的思考空間與時間,學生的理解才能深入,表達才能具體,最終用自己的經驗創造性地解決了問題。
四、溝通計數單位內在聯系
教學片斷三:認識整千數。
師:認識了1000,以千位單位繼續往下數,你會數嗎?
生:會數,1000、2000、3000、4000……
師:4000用乘法算式怎么表示呢?
生:1000×4=4000。(板書:1000×4=4000)
師:你有沒有發現這些算式非常像?一起讀一讀,你發現它們有什么特點和聯系嗎?
生 :10 ×4=40,100 ×4=400,1000×4=4000。
生:我發現這些算式有規律。乘數依次增加1個零,積也依次增加1個零。
師:是的,還有不一樣的表達嗎?
生:我發現這些算式都有一個乘數是4,這個4就是一個“加工廠”,1個十×4=40、1個百×4=400、1個千×4=4000。
師:“加工廠”這個詞真是形象!還有人說這些算式都與1×4=4有關,你覺得有道理嗎?
生:有道理,我也是這樣想的。
師:如果把這些算式看作一個家族,那么1×4=4你怎么理解?
生:是祖先!
生:是起源!
生:是基因!
師:再來個新成員,往下說!
生:10000×4=40000。
師:同學們真了不起!能把這些不同的算式溝通和聯系。溝通聯系是數學學習非常重要的方法,能溝通聯系也說明你已經領悟了!
“溝通計數單位的內在聯系,掌握相同的數學結構”是這節課的另一個重要目標。我們為什么要認識更大的計數單位?從本質上講,任何一個數都可以通過1個、1個數出來,但是效率太低了,所以發明了更大的計數單位,10個、10個數,100個、100個數,1000個、1000個數,提高計數和計算的效率。因此,溝通不同計數單位的內在聯系,能讓學生的學習從“個”上升到“類”,從本質上認識它們具有相同的數學結構。10×4=40、100×4=400、1000×4=4000,這些算式都可以理解成:“1×4=4”,也就是 1個計數單位×4=4個計數單位。掌握了這樣的本質結構,就能以此類推,得到更多的整百整千數。
教學研究需要討論的兩個問題是“教什么”和“怎么教”。教什么?教師只有深入數學本質,才能抓住核心問題,引導學生步步深入地探尋數學的本質。怎么教?教師只有溝通知識的內在聯系,引導學生遷移、類比、概括和歸納,方能點燃學生思維的火花,讓課堂綻放更加絢麗的生命力。

