經歷探究算理算法過程促進思維深度發(fā)展

高春霞

在計算教學中，算理和算法相輔相成、共同作用。算理，是計算的原理，是解決“為什么這樣算的問題”。算法，是計算的方法，是解決“怎么算”的問題。我們知道，算理是學生走向算法的橋梁，是學生學習算法的基礎；算法是對算理的提煉和概括。因此，我們在計算教學中要做到算理與算法并重，要正確處理算理與算法的關系，讓學生經歷理解算理的過程，在理解算理的基礎上掌握計算方法，正所謂“知其然、知其所以然”，使學生獨立思考與深層感悟，從而提高學生的計算能力，促進學生的思維發(fā)展。

下面結合自己的教學體會談談在計算教學中如何將算理與算法有機地結合。

一、動手操作，讓學生經歷算理和方法的探索過程

《數學課程標準》在課程理念中提出：學生應該有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動的過程。因此，我們要注重讓學生經歷計算的活動過程。也就是說在我們的教學中不僅要關注方法和結果，更要關注獲得方法和結果的思維過程，學生不僅僅要掌握計算的方法，更重要的是能夠理解運算的算理。

在傳統(tǒng)的計算教學中，計算方法是教師傳授的，然后學生根據教師提供的方法和結論模仿例題做些類似的題目，至于計算方法是怎么產生的，學生是怎么想的極少考慮。學生掌握并理解算理，是計算教學的靈魂。蘇霍姆林斯基說過：在人的心靈深處，總有一種根深蒂固的需要，這就是希望自己是一個發(fā)現者、研究者、探索者。因此，我們在教學過程中不能束縛學生思維的發(fā)展，而應該創(chuàng)造出更大的空間和平臺，讓學生發(fā)揮他們的創(chuàng)造性思維，主動參與計算原理和方法的探索，促進學生思維的發(fā)展。如在低年級教學中借助小棒操作，經歷探究算理和算法的過程，讓算理與算法有機結合。

在教學45+3時我是這樣設計的：

師：45+3=？你會算嗎？

生 1：等于 75。

生2：應該是等于48，4不能與3相加。

師：那45+3到底等于多少呢？請同學們拿出小棒，擺一擺，看一看自己能不能解決。

匯報交流：

師：誰來說一說怎樣算？

生：先算5+3=8，3根小棒與5根小棒合起來是8根小棒，再算40+8=48，40根小棒與8根小棒合起來就是48根小棒。

……

師：43+5=？

生：3+5=8，40+8=48。

師：你們發(fā)現什么規(guī)律了嗎？

生：個位上的數與個位上的數相加，再與40相加。

……

在探究中，要發(fā)揮學生的主體作用，教師要把握時機，為學生計算指明方向，即時鼓勵學生，直至探索成功。學生利用自己的語言總結了算法：“捆加捆，根加根”。學生經歷了探究的過程，將算理與算法有機地結合，有利于提高學生的計算能力。

在進位加法、退位減法的教學中，小棒更是起到了很好的作用，學生在不斷地捆、拆中理解了算理，掌握了計算的方法。我們還要引導學生在頭腦里想一想自己的操作過程，并用自己的語言表述出來，幫助學生實現“實物操作”向“算法操作”的自然過渡，讓學生體驗從直觀到抽象的逐步演變過程，逐步擺脫對操作的依賴，促進學生抽象思維能力的發(fā)展。

二、自主探究，找準算理與算法的連接點

處理好算理與算法的關系對于突出計算教學核心，抓住計算教學關鍵具有重要的作用。如何處理好兩者之間的關系又是一個難點。在教學中要注重算理與算法的有機統(tǒng)一，形式上可分，實質上不可分，重算法必須重算理，重算理也要重算法,算法形成不能依賴形式上的模仿，而要依靠對算理的透徹理解，只有在真正理解算理的基礎上掌握算法、形成計算技能，才能找到算理與算法的平衡點。因此，教師必須對學生的知識、能力做全面的了解，要對教材內容做細致的分析，把握教學的探究點，找準時機，巧設新舊知識的矛盾沖突，引導學生走進問題情境，讓學生在參與中找出新舊知識的連接點，感悟出算理，探究出計算的新方法。

如教學 12×3的豎式筆算時，學生已經知道12×3的算理實際就是3個2和3個10的和。即 3×10=30，3×2=6，30+6=36，于是教師引導學生：根據算理用豎式表達出來，從而引出乘法的原始豎式：

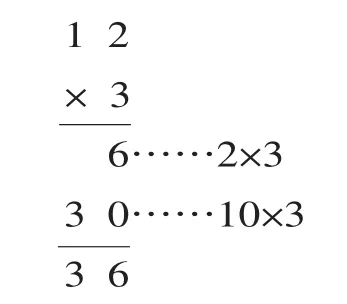
再讓全體學生回顧計算過程，加深對算理的理解，在學生對算理有一定理解的基礎上，引導學生對計算過程進行反思，啟發(fā)學生再思考，對算理進行提煉和“創(chuàng)造”，從而對上面的豎式進行簡化：

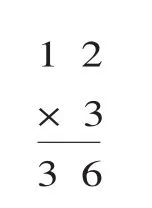
算理為計算提供了正確的思維方式，保證了計算的合理性和正確性，算法為計算提供了快捷的操作方法，提高了計算的速度。算理是算法的理論依據，算法是算理的提煉和概括，它們是相輔相成的。

再如在教學《兩位數乘兩位數》時，“24×12”的豎式計算如下：

教學中教師充分抓住豎式中“24”的轉接理解，把學生帶入探究活動中。有學生說：因為12中的“1”是表示 10，“1×24”實質是表示10×24等于240。有學生說：“24”后面還有一個隱形的零。本課是《兩位數乘一位數》向《兩位數乘兩位數》新舊知識的跨越，也是小學生學習由兩位數乘一位數向兩位數乘兩位數計算的重要轉折點，如果教師找準了這一關鍵的連接點，學習效果自然事半功倍。只有根據學生已有的“舊知”，并與抽象的豎式計算建立起聯系，從而讓學生經歷豎式的形成過程，清晰理解豎式的算理，才能真正掌握豎式計算的方法。

三、優(yōu)化算法，加強算理與算法之間的聯系

《數學課程標準》指出：“由于學生的生活背景和思考角度不同，所使用的方法是多樣的，教師應尊重學生的想法，鼓勵學生獨立思考，提倡計算方法的多樣化。”“提倡算法多樣化”是實踐數學新課程改革理念的一項重要舉措。算法多樣化不是教學的最終目的，在算法多樣化的基礎上，還要進一步比較、歸納，對計算方法進行優(yōu)化，形成較為高效的方法，并對一些基本的運算通過多種方式達到熟練。所以，算法多樣化不單單是要“多樣”，而必須是要“有用”。在計算過程中，理解算理是計算的前提，而算法優(yōu)化則是計算的關鍵。但往往一節(jié)課下來，方法是“多樣化”了，但學困生連基本的方法都沒掌握好。

如“9加幾”的教學片斷：

師：9+5＝？ 5+9＝？

師：你們有什么辦法算一算嗎？

（大家可先自己用學具擺一擺，給你的同桌說一說，或選用自己喜歡的方法來解決）

（教師巡視，聽取學生的不同算法，引導學生積極參與）

師：誰來說說你是怎樣算的？

生：我從5根小棒中拿出1根給9根的小棒，湊成10，還剩下4根，合起來是14根。

師：為什么你先將1根與左邊的放一起？

生：因為9和1正好湊成10。10+4比較好算。

師：湊成十！（邊說邊板書）

生：我是從9根里拿5根過去，這樣右邊也正好是10，合起來就是14根。

師：你也很棒！

師：你們認為哪一種方法簡單些？為什么？

生：第一種，因為只拿1根就可以湊成十。

將學生自主探索多樣化與教師引領算法優(yōu)化巧妙結合起來，在諸多算法的基礎上突出最優(yōu)的算法，在學生理解這種算法的算理基礎上，以這種算法為主進行訓練，從而來提高學生的計算能力，促進學生的思維發(fā)展。