基于等價Fisher信息矩陣的AUV集群網絡導航精度分析

張立川,王永召,屈俊琪

(西北工業大學 航海學院,陜西 西安,710072)

0 引言

可靠的位置信息是自主水下航行器(autonomous undersea vehicle,AUV)完成水下各項工作的基礎,在 AUV集群協同導航中,研究信息在AUV之間的傳遞規律,對于提高AUV的協同導航精度具有重要意義。在協同系統中,領航AUV通過高精度傳感器可較為精確地獲取自身的位置,而跟隨 AUV由于只裝備了低精度傳感器,所以必須依靠先驗信息、自身量測信息以及和領航AUV或同伴跟隨AUV協作來估計自身的位置。

AUV集群的協同定位屬于網絡協同導航范疇,網絡協同導航主要指導航網絡內的各個節點單元通過獲取網絡內其他節點單元的信息后加以融合,根據自身的先驗信息和量測來估計自身的位置。國內外大多數學者研究了單個領航艇和單個跟隨艇信息融合的定位誤差和導航算法。文獻[1]研究了無跡卡爾曼濾波的協同導航算法。文獻[2]研究了AUV集群編隊構型對定位誤差的影響,但是分析模型具有一定的單一性,對于 AUV集群協同導航來說,不會只是局限于此,從信息論和網絡協同導航的角度出發,AUV集群協同定位誤差模型應具有更為精確的建立。文獻[3]研究了基于信念傳播的無人機協同網絡導航算法,無人機利用整個編隊信息的融合進行協同定位,極大提高了定位精度,說明網絡協同導航在無人機的協同導航中已經有所研究。文獻[4]從Fisher信息矩陣的角度出發,論證了網絡協同導航系統每個節點的Fisher信息矩陣包含模型的先驗信息、時間協同信息和空間協同信息。文獻[5]從Fisher信息矩陣的角度出發,給出了網絡協同導航典型節點模型的空間協同、時間協同以及信息融合的定量分析,證明了當信息量越多時,節點的定位精度越高。

基于之前的研究,文中進一步研究了 AUV集群的網絡導航方式,提出了4種典型的AUV集群網絡導航模型,并引入等價Fisher信息矩陣等相關理論,分別對 4種模型的定位誤差影響因素和定位誤差界進行了分析和理論驗證,通過理論和仿真試驗證明:AUV集群在空間和時間上的相對位置關系是影響集群定位精度的重要因素,下文將對AUV集群的網絡導航精度做具體分析。

1 AUV集群網絡導航模型

AUV集群網絡導航模型如圖1所示。圖1(a)為單個跟隨 AUV在某個時刻tk根據水聲測距和通信從空間中若干個領航 AUV獲得定位信息,從而確定自身的位置,其中Na≥2 。圖 1(b)是以圖1 (a)為基礎的進一步研究,圖1 (a)只研究了空間內某個時刻跟隨AUV的定位誤差,而圖1 (b)既考慮了空間信息,同時又將時間上的位置轉換考慮在內。圖1 (c)同樣研究跟隨AUV在某個時刻tk的定位誤差,與圖1 (a)不同的是,圖1 (c)增加了2個跟隨AUV之間的信息融合。圖1 (d)中將跟隨AUV設定為3個,例如:跟隨AUV1不僅從領航AUV,相鄰跟隨AUV2、AUV3之間獲得信息,由于AUV2、AUV3之間也相互通信,AUV2、AUV3融合后的信息最終也會被跟隨AUV1獲得。

圖1 集群AUV網絡導航模型Fig.1 Network navigation models of AUV swarm

2 Fisher信息矩陣網絡導航分析

首先引入Fisher信息矩陣建立AUV集群網絡導航誤差模型,之后建立圖1中4種典型網絡導航模型的等價 Fisher信息矩陣[6],并根據等價Fisher信息矩陣對相應網絡導航模型的定位精度進行詳細分析。

2.1 理論基礎

假設在 AUV集群導航網絡中有一系列跟隨AUVi,用定義跟隨AUVi在tn時刻的狀態,其中通過 AUV之間的水聲量測量,信息傳遞以及 AUV的先驗信息來估計AUVi的位置信息。

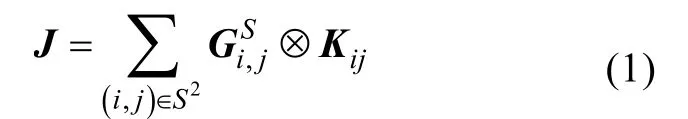
其中,?為克羅內克積算子,所以S階矩陣的k×r階子矩陣可表示為

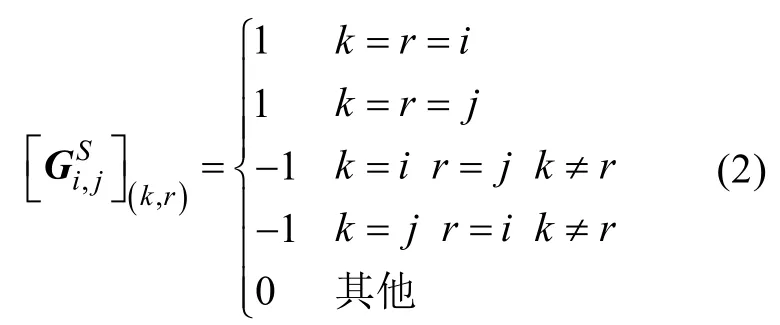
另Kij取決于AUV集群在狀態i和狀態j的先驗信息和量測信息,且Kij=Kji,如果Kij=0,說明AUV集群在狀態i和狀態j之間沒有先驗信息和量測信息。如果i=j,則Kii只和AUV集群的狀態i有關。

2.2 信息融合模型

AUV集群信息融合的方式分為空間協同、時間協同和空時協同。文中只研究前 2種,跟隨AUV通過自身的先驗信息、領航AUV及其他跟隨AUV的位置信息來估計自身的位置。

圖1(a)為空間域內 1個跟隨AUV和若干領航AUV的信息融合圖,跟隨AUV從每一個領航AUV所獲得信息的Fisher矩陣為其中因此基于式(1)的 Fisher信息矩陣為

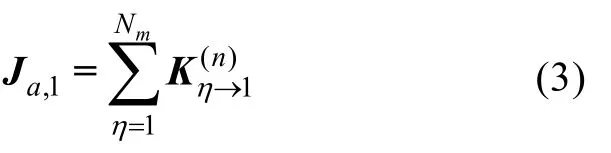
圖1(b)為時間域內1個跟隨 AUV和若干領航AUV的信息融合圖,跟隨AUV在2個不同時刻t1和t2通過和領航 AUV信息交換以及自身傳感器測量來確定自身的位置狀態和,自身傳感器所獲得信息的 Fisher矩陣為其中因此基于式(1)的Fisher信息矩陣為

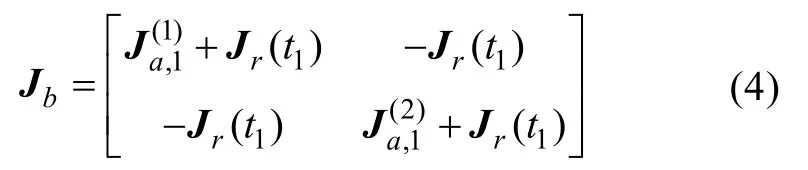
圖1(c)為空間域內2個跟隨AUV和若干領航AUV在t1時刻的信息融合圖,且需要考慮2個跟隨AUV之間的信息融合。2個跟隨AUV的位置狀態為和,2個跟隨AUV通過水聲量測的 Fisher信息矩陣為因此基于式(1)的Fisher信息矩陣為

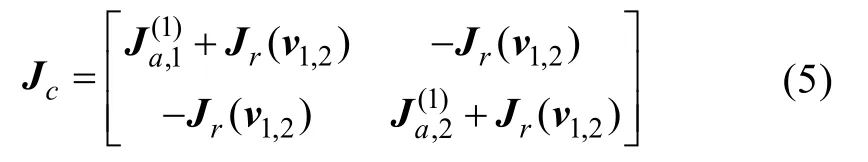
圖1(d)為3個跟隨AUV和若干領航AUV在空間上的信息融合圖。跟隨 AUV1不僅從領航AUV,相鄰跟隨 AUV2、AUV3之間獲得信息,由于AUV2、AUV3之間也相互通信,AUV2、AUV3融合后的信息最終也會獲得。跟隨 AUV的位置狀態為和,跟隨 AUV之間通過量測的信息矩陣為

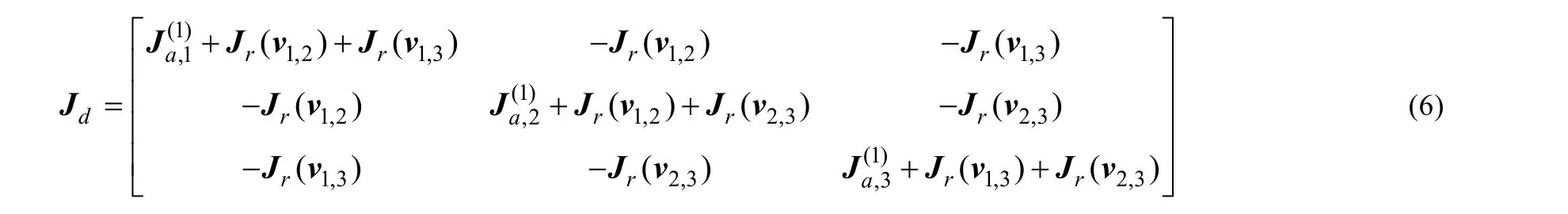
2.3 定位誤差界

基于2.2節分析的結果,分別研究在網絡導航模型(a)～(d)的導航系統中,單個 AUV通過信息融合后的定位誤差界。所以需要將第2.2節中AUV集群的 Fisher信息矩陣進行轉換得到單個AUV的等價Fisher信息矩陣和定位誤差界。

1)圖 1(a):由式(3)可以得到跟隨 AUV 的Fisher信息矩陣為

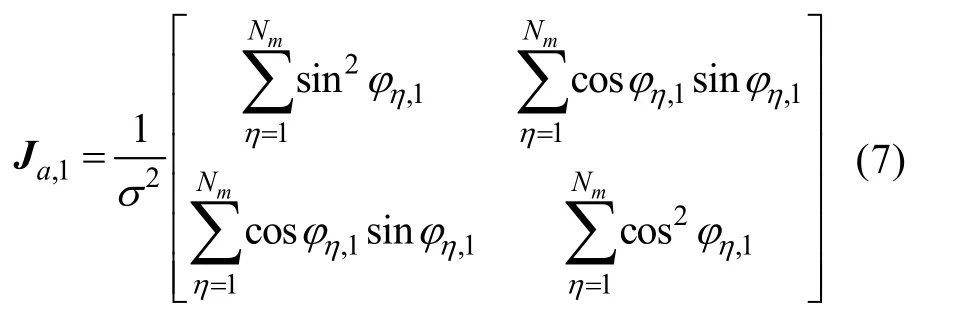
所以跟隨 AUV的平方位置誤差界(squared position error bound,SPEB)為

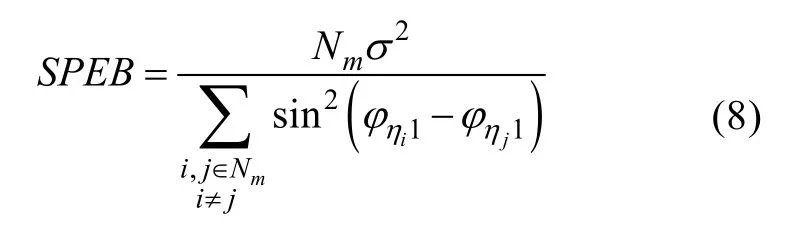
根據式(7)和式(8)對跟隨 AUV的定位誤差做出討論。

①η越大,即當空間領航 AUV越多時,tr(Ja)越大,此時跟隨AUV的定位誤差界越小。

② 當η=2時,此時空間內有2條領航AUV,當時SPEB最小,即2個領航AUV和跟隨AUV成90°(見圖2),定位誤差界最小。

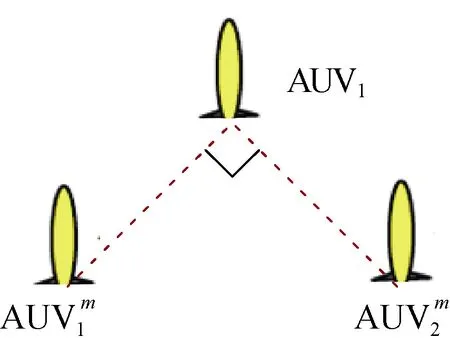
圖2 雙領航AUV協同最優編隊構型Fig.2 Optimal cooperative AUV formation configuration with dual leader AUVs

③ 當η=3,4,…,Nm時,由式(8)可知,使各個領航AUV以跟隨AUV為坐標原點成最多兩兩互成90°排布,如圖3所示,此時可以得到最小的SPEB。

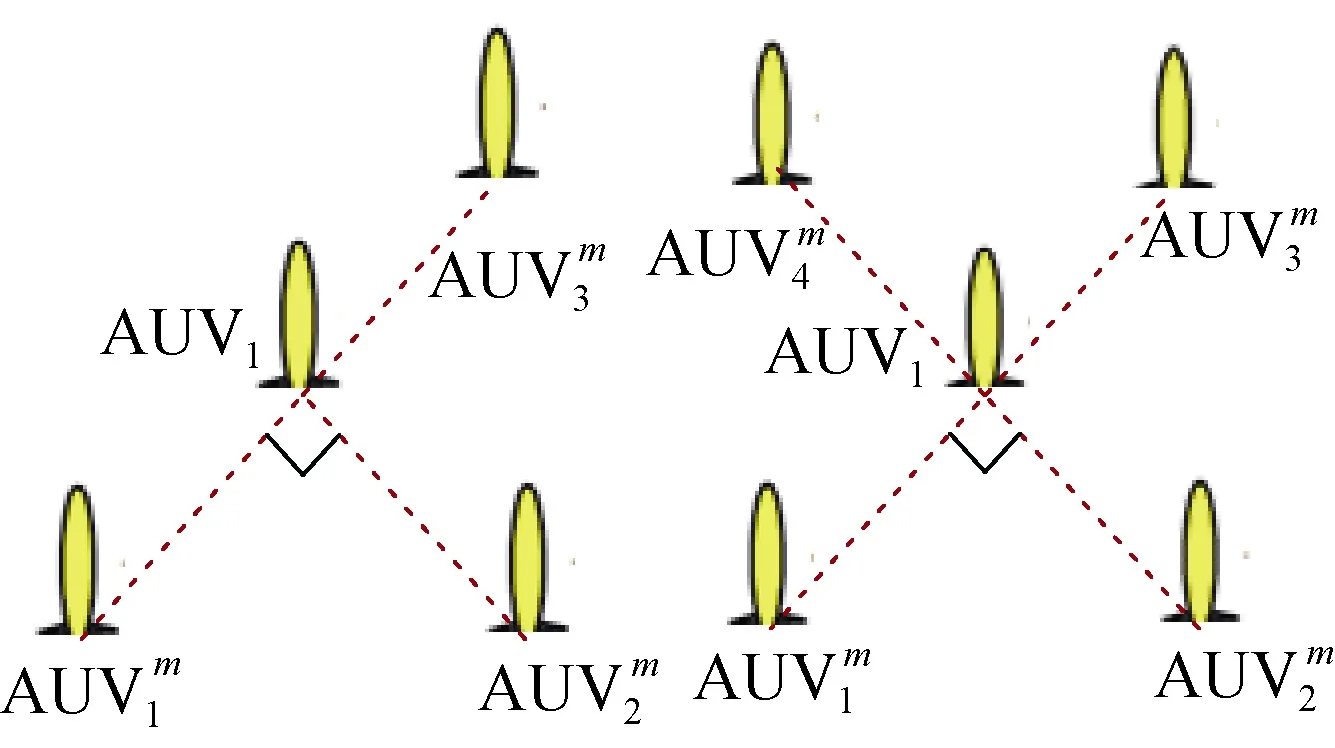
圖3 多領航AUV協同最優編隊構型Fig.3 Optimal cooperative AUV formation configuration with multiple leader AUVs

2)圖 1(b):根據式(4)跟隨 AUV 在時刻tk+1的等價Fisher信息矩陣為

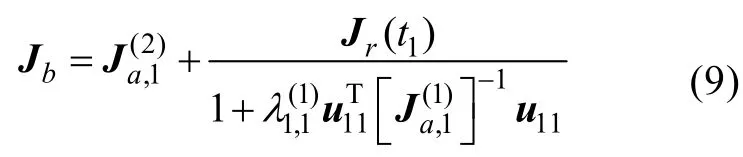
① 當Jr(t)=0時,說明跟隨 AUV完全沒有從自身傳感器獲取量測信息,而是單純依靠領航AUV完成自身定位,此時

④ 若忽略跟隨AUV在航行時的航位推算誤差,則在t2時刻,跟隨AUV的Fisher信息矩陣為假設空間內只有 1個領航AUV和 1個跟隨 AUV,分析系統在t2時刻跟隨 AUV的誤差情況,對應的Fisher信息矩陣為

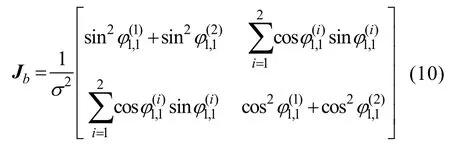
所以跟隨AUV平方位置誤差界為

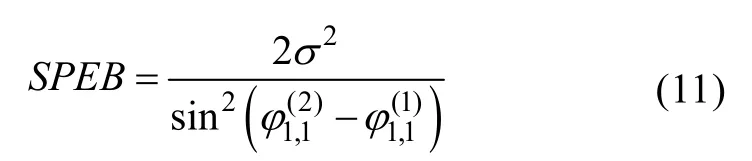
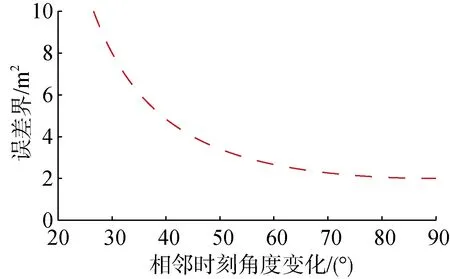
圖4 平方位置誤差界Fig.4 Square position error bound(SPEB)

所對應的編隊構型如圖5所示。

3)圖 1(c):由式(5)可得,跟隨 AUV1的等價Fisher矩陣為

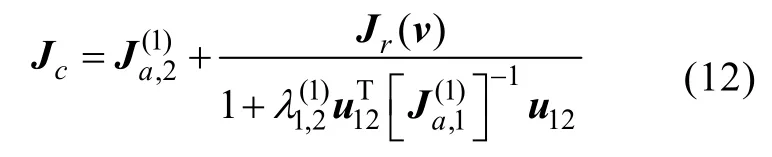
算例:假設跟隨AUV1,AUV2和領航AUV在空間的位置分別為(0,-2)、(2,0)和(0,2),假設跟隨 AUV1從領航 AUV處獲得的信息矩陣為量測方差σ2=1,由式(12)可以計算得到跟隨 AUV1的 Fisher矩陣,將其表示為信息橢圓[7]的形式,橢圓面積代表了在對參數估計的過程中信息量的大小和誤差范圍。跟隨 AUV信息融合前后的信息橢圓如圖 6所示,由信息橢圓面積可知,當增加跟隨 AUV之間的信息融合時,可以提高導航系統的定位精度。

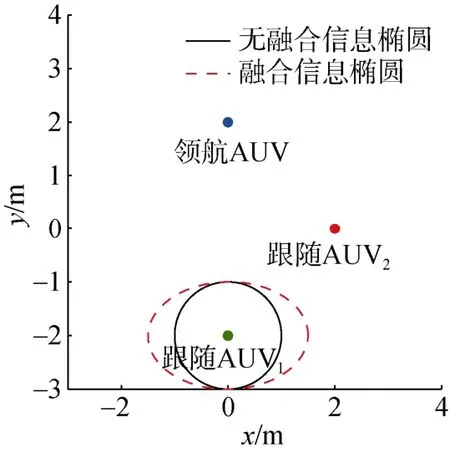
圖6 信息融合前后信息橢圓對比Fig.6 Comparison between information ellipses before and after information fusion

4)圖1(d):為3個跟隨AUV在空間內的信息融合,Fisher信息矩陣如式(6),由于等價Fisher信息矩陣形式十分復雜,文中不再詳述。

3 數值仿真與分析

下面通過數值算例分別對2.3節分析2)中的結論④和2.3節分析3)來進行仿真驗證。

1)算例1:假設空間有1個領航AUV從(0,0)處開始航行,航速 2 m/s,1個跟隨 AUV同時從(-500,0)處航行,航速2 m/s。假設測距誤差0.1 m,跟隨 AUV速度傳感器的誤差 0.1 m/s,角度誤差0.1°,位置誤差 1 m,采樣周期 10 s。

試驗組:領航AUV的航向為北偏東30°,跟隨 AUV航向正北,之間產生相對觀測角度變化;對照組:領航AUV航向正北,跟隨AUV航向正北,之間未發生相對觀測的角度變化。2組試驗均采用EKF協同定位算法計算2個AUV的軌跡及誤差,結果如圖7～圖10所示。

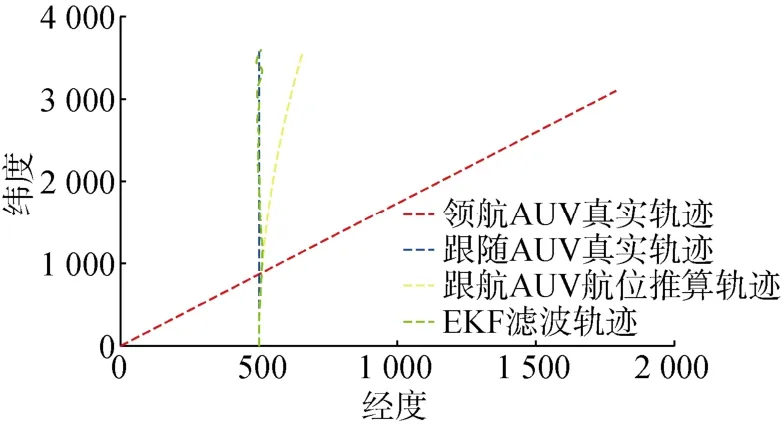
圖7 試驗組AUV協同定位軌跡Fig.7 Tracks of AUV cooperative location for test group

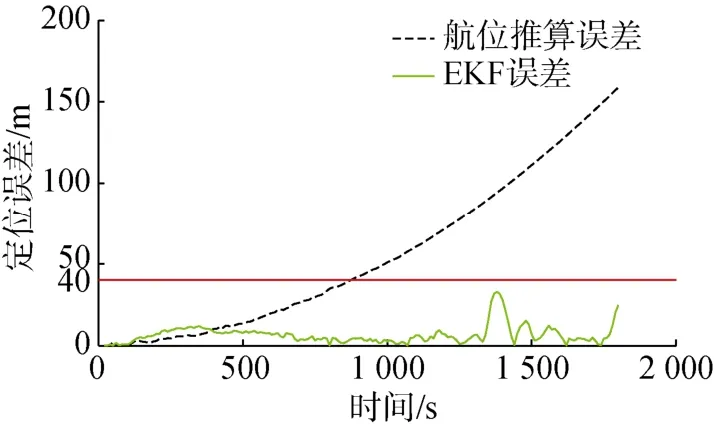
圖8 試驗組AUV協同定位誤差曲線Fig.8 Curves of AUV cooperative location error for test group

在試驗組中,跟隨AUV和領航AUV之間有相對角度變化(見圖7),所以圖8中的定位誤差波動小,且定位更加精準;而在對照組中由于跟隨AUV和領航AUV之間沒有發生相對角度的變化(見圖9),所以圖10中的定位誤差波動較大。

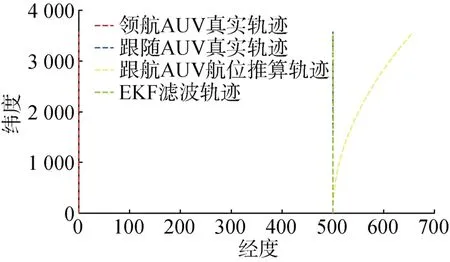
圖9 對照組AUV協同定位軌跡Fig 9 Tracks of AUV cooperative location for contrast group

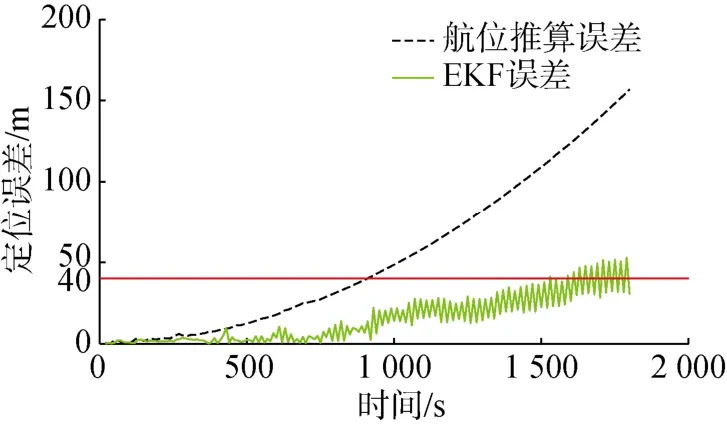
圖10 對照組AUV協同定位誤差曲線Fig 10 Curves of cooperative localization error of AUV of contrast group

2)算例2:假設空間有1個領航AUV從(0,0)處沿著正北方向航行,航速5 m/s,2個跟隨AUV分別從(-500,0)和(500,0)沿著正北方向航行,航速分別為1 m/s和2 m/s。假設測距誤差5 m,2個跟隨AUV的速度傳感器誤差為0.1 m/s,角度誤差0.1°,位置誤差1 m,采樣周期1 s。

試驗組:2個跟隨AUV之間通過水聲通信進行信息融合;對照組:2個跟隨AUV之間沒有信息融合。試驗組采用基于擴展卡爾曼濾波(extended Kalman filter,EKF)的信息融合算法對跟隨AUV2進行定位,對照組采用EKF協同定位算法,跟隨AUV2的定位誤差如圖11所示。

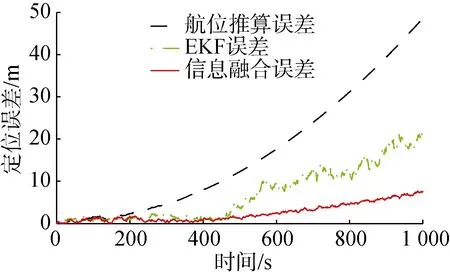
圖11 跟隨AUV2協同定位誤差對比曲線Fig.11 Contrast curves of cooperative location error for follower AUV2

由圖11可知,與單純依靠領航AUV相比,增加跟隨AUV之間的信息融合可以極大地提高定位精度。

4 結束語

文中提出了4種AUV集群協同定位的信息融合典型節點圖,并且引入等價 Fisher信息矩陣等理論對影響誤差的因素進行了分析,當各領航AUV和跟隨AUV之間的方向向量最多兩兩互成90°時,此時跟隨AUV的定位精度最高;當跟隨AUV在相鄰觀測時刻和領航AUV的方向向量夾角越大,定位精度越高,且最高定位精度的夾角為90°;增加跟隨 AUV之間的信息融合,利用整個編隊的信息對跟隨 AUV進行定位,可以提高定位精度。

為了使得網絡導航誤差模型更加完善,仍需要對增加更多跟隨 AUV的空間網絡導航誤差以及空時網絡導航誤差進行分析;需要將文中理論應用到具體的網絡導航算法中分析 AUV集群的實時導航誤差。