井地2.5維DC反演研究

付德俊

(廣東核力工程勘察院， 廣州 510800)

0 引言

直流電阻率法(DC)是利用地下介質的電阻率參數來實現對地下地質結構的分辨和研究，該方法被廣泛應用到環境與工程勘察中，其已成為目前常用的物探方法之一。

常規直流電阻率法將觀測電極布設在地表，來觀測地表電位的變化，并采用特定觀測裝置來刻畫出需要的參數(如視電阻率等)，顯示出地下地質體在水平或垂直方向存在電性差異，從而實現對地質體的定性分析。但是，對于特殊地質情況，地表觀測到電位或視電阻率數據很難對深部地質體進行約束，較難地刻畫地下地質體的邊界范圍，無法滿足中深部工程勘察需求，為了彌補這一缺陷，開展井地直流電阻率法反演成像研究具有重要的研究意義，其彌補了縱向上深部數據對地下地質體約束。

井地直流電阻率常用的觀測裝置可以分為井-地、地-井-地、井-井以及井-地-井等，為了研究不同觀測裝置對地下地質體的分辨能力，具有重要意義。目前，國內、外研究學者進行很多相關的研究工作，Zhou等[1-2]采用解析偏導數矩陣完成了2D/3D井間DC快速成像研究；Wikinson等[3]重點分析了礦井DC反演成像技術的研究工作；國內學者同樣在這方面做了大量的研究工作；王志剛等[4-6]實現積分方程法的Born 近似井地DC三維快速成像研究；呂玉增等[7]實現了井間三維直接成像研究；岳建華等[8]開展了巷道井地DC快速成像研究；徐凱軍等[9]開展了基于共軛梯度算法的三維井地電阻率成像研究；藍澤鸞等[10]開展了基于TV約束的2.5維井地直流電阻率反演研究。

筆者采用變分原理推導2.5維井地DC滿足邊值問題，構建了基于二階最大平滑因子的井地DC正則化反演目標函數，采用共軛梯度算法實現了該目標函數最優化求解，最終完成不同觀測方式的井地2.5維直流電阻率穩定、高效的反演研究。研究結果表明，不同觀測方式的反演對異常體的約束存在明顯的差異，靠近井所在的位置對異常體的約束較為明顯，但是若沒有地表數據的約束可能出現對異常體過渡約束，使異常體的范圍出現明顯的偏差。

1 井地2.5維直流電阻率正演

1.1 邊值問題

在波數域，井地2.5維DC滿足的邊值問題[11]如式(1)所示。

(1)

式中:區域Ω為二維研究區域；Γs、Γ∞是二維區域的邊界，Γs為區域Ω的地表邊界，Γ∞為區域Ω的地下邊界；σ為電導率；r為點電源到邊界的距離；n為無窮遠邊界的外法向方向；k為波數；K0、K1分別為零階、一階第二類貝塞爾函數。

將公式(1)轉化為變分問題：

Iδ(A)U]dΩ+

(2)

對計算區離散、構造插值函數，式(2)離散為：

(3)

其中，P為除供電點為0.5以外全為零的列向量。

對式(3)求變分并令其為零，得到線性方程組

KU=P

(4)

通過求解線性式(4)，得到波數域的電位U，然后通過傅氏反變換得到電位：

(5)

式中:r為點的位置；km是波數；gm是加權系數[11]。

表1 傅氏變換系數km和gm

1.2 2.5維井地DC觀測方式

常用的井地DC觀測裝置可以分解成一下四種：①井-地；②地-井-地；③井-地-井；④井-井測量裝置，其野外布置方式圖1所示。

圖1 2.5維井地DC觀測裝置示意圖Fig.1 Schematic diagram of2.5-D well ground DC observation device(a)井-地;(b)地-井-地; (c)井-地-井;(d)井-井

2 共軛梯度正則化反演

構建正則化反演目標函數[12]：

φ(m,α)=φd(m)+αφm(m)

(6)

其中：φ(m,α)為構建的正則化目標函數；α是正則化因子；φd(m)為數據約束項；φm(m)為模型約束項；m為模型參數。數據約束項與模型約束項表達式分別為：

φd(m)=Wd(A(m)-dobs)TWd(A(m)-dobs)

φm(m)= (m-mapr)T(m-mapr)

(7)

其中：A表示為正演算子；dobs表示為觀測數據；mapr為已知地下結構的先驗信息；Wd為數據權重矩陣。為了獲得最優的解，必須對正則化目標函數求最小，即

φ(m,α)=φd(m)+αφm(m)→min

(8)

筆者采用共軛梯度算法求解公式的最優化問題，其采用的基本思想為最速下降法[13]：

mn+1=mn+Δm

(9)

初始梯度迭代向量表達式為：

(10)

首次迭代方向為梯度向量與首次迭代共軛梯度向量的線性組合

(11)

第n+1次迭代的方法為：

(12)

采用線性搜索求解目標函數最小來獲取最速下降迭代步長：

(13)

通過簡化，可獲取到下降步長為式(14)。

(14)

3 算例分析

3.1 算法驗證

圖2展示了電導率為0.01 s/m均勻半空間的理論電位曲線與數值模擬的電位曲線對比圖，相對誤差范圍在2%以內,對比結果表明本文正演算法正確可靠。

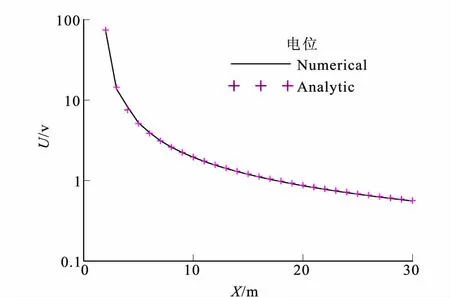
圖2 數值解與解析解電位對比曲線圖Fig.2 Comparision of FEM numerical and one- dimensional analytical solutions

圖3 地電模型斷面圖Fig.3 Sectional view of the electric model

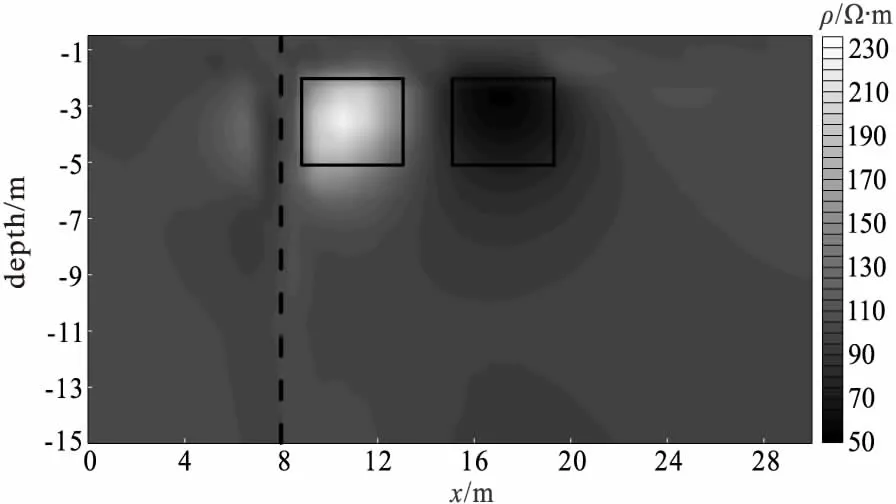
圖4 井-地反演斷面圖Fig.4 Sketch map of borehole-surface dc resistivity

圖5 地-井-地反演斷面圖Fig.5 Sketch map of surface-borehole- surface dc resistivity

圖6 井-地-井反演斷面圖Fig.6 Sketch map of well - to - well dc resistivity

圖7 井-井反演斷面圖Fig.7 Sketch map ofcrosshole dc resistivity

3.2 不同觀測方式反演對比分析

圖3為地電模型，均勻半空間下存在埋深以及大小相同而不同電導率的兩個異常體，異常體1的電導率為0.005 s/m ，異常體2的電導率為0.02 s/m，背景電導率為0.01 s/m，異常體尺寸為4 m×4 m，異常體的頂部埋深為2 m，設計了如上所述的四種井地直流電阻率的觀測方式，圖(4)～圖(7)的虛線表示井設計的位置。理論正演得到的合成數據(直接采用觀測電位作為數據來源)加入3%的高斯白噪聲后作為反演輸入數據，此次反演網格與正演網格一致，網格大小為42×20，并向外進行了網格延拓以降低截斷邊界帶來的數值誤差。采用Pole-Pole采集裝置，對于井-地測量方式總電極數為20個，地表布設12個，井中布設8個；地-井-地測量方式總電極數為24個，地表布設16個，井中布設8個；井-地-井測量方式總電極數為32個，地表布設16個，井中布設16個；井-井測量方式總電極數為16個，地表布設0個，井中布設16個。最后采用共軛梯度法實現了不同觀測裝置的井地電阻率2.5維二階平滑模型正則化反演研究。

圖4～圖7分別展示了井-地、地-井-地、井-地-井以及井-井四種觀測方式的反演結果。此次反演最大迭代次數為20次，圖8、圖9分別展示數據誤差與迭代次數的衰減圖以及正則化因子α與迭代次數的變化曲線。從反演結果中可以看出，反演結果都能夠較好體現異常所在的位置，反演結果較為明顯。但是對于不同觀測方式其反演結果得到細節不一樣，對異常體邊界的識別程度不一致。從圖4的反演結果可以看出，靠井所在位置的異常體，其反演的結果呈現的范圍更加集中，而遠離井的異常體反映的區域相對較大。圖5展示了地-井-地的觀測裝置的反演結果，當井位于兩個異常體的中間時，井所采集的數據對兩個異常體都存在約束，兩個異常體都能較為明顯分辨。對比圖4～圖5可發現，地-井-地的觀測方式相對井-地方式提高提高了異常體的分辨率，其對井旁左右的異常體都有較好地約束，而井-地觀測方式對靠近井的異常體約束權重相對大。

圖6井-地-井觀測方式的反演結果表明，異常體的邊界相對前兩種的反演結果更為集中，反演的結果與實際模型的吻合度高，反演得到的電阻率值與真實電阻率值相差不大。圖7的井-井觀測方式的反演結果表明，其反演得到的異常體范圍與真實結果相差較大，由于缺乏地表數據的約束導致異常反演趨向井所在的位置，井附近的細節較為明顯，總體上異常體相應位置得到體現。從圖6～圖7的對比發現，地表觀測數據能夠較為全面進行約束，避免了過渡依賴井中數據，避免假異常的存在。

綜合分析圖4～圖7的結果可以表明，井中數據能夠較好彌補地表觀測數據對縱向約束減弱的缺陷，同時能夠提高反演非唯一性。從反演的結果表明，井-地-井的觀測方式對異常體的邊界圈定相對其他三種觀測方式較好，但是存在一些小的細節異常，地-井-地觀測方式能夠較好對井兩旁異常體都有較好的約束效果，而遠離井的異常體其約束能力逐漸降低，這一現象在井-地測量方式得到體現。

圖8、圖9分別展示了數據誤差隨迭代次數的增加而逐漸減小，正則化因子α隨迭代次數的增加而逐漸減小的這一規律。當模型達到一定時，即隨著迭代次數的增加人為的減少模型約束權重，使反演結果更加傾向對數據的擬合來降低反演的數據誤差，最終達到穩定的反演結果。

4 結論

不同觀測方式的井地電阻率2.5維共軛梯度反演結果表明，我們開發的算法正確可靠，反演算法穩定高效。根據以上的研究可以得出以下幾點認識：

1)井中數據能夠較好彌補地表觀測數據對縱向約束減弱的缺陷，能夠有效地降低反演非唯一性，同時井-地-井觀測方式所采用電極數量大于其他觀測方式，其獲得的地下異常體信息較為豐富，其反演的異常范圍更為集中，其對異常體的圈定要優于其他觀測方式。

圖8 數據誤差與迭代次數曲線圖Fig.8 Curve of between iterationserror and iterations

圖9 正則化因子α與迭代次數變化曲線圖Fig.9 The graph of the change of regularization factor and iteration number

2)由于地表測量電極的缺失，導致井-井觀測方式在橫向上對異常體的約束減少，數據量的減少很大程度上增加反演的非唯一性，導致反演精度差，使得井的左右兩側出現假異常，但也能大致地反應異常的范圍，能夠給實際情況提供參考。

3)基于平滑約束的二階最大平滑穩定因子的共軛梯度法迭代反演方法，能夠較為穩定獲取反演結果，同時模型約束項增加提高反演的穩定性，其為后期開發更為穩定模型約束項提供借鑒。