基于常Q模型的分數階粘彈介質數值模擬方法

楊佩城， 韓立國， 蔡中正

(吉林大學 地球探測科學與技術學院，長春 130026)

0 引言

地震波在實際地下傳播過程中，經歷了大地濾波作用后，將導致能量的衰減和相位的錯動。能量的衰減將嚴重影響勘探的深度；相位的錯動則將影響構造位置的確定。早期的波場模擬和成像并未考慮這些衰減因素，對油氣勘探造成了一定程度的誤導。隨著近年來勘探精度要求的提高，基于粘滯波動方程的正演和偏移算法也已經得到越來越多的重視。Kjartansson[1]提出的常Q模型，認為與地震勘探頻率有關的頻段內，Q值不隨頻率變化。近些年常Q模型得到了廣泛地研究和應用。Zhang等[2]提出了一種基于Kjartansson常Q模型的分數階粘彈性波動方程，該方程中相位校正項與衰減補償項是解耦的；Deng 等[3]研究了基于標準線性體模型的逆時偏移衰減補償，此方法能夠在地震波傳播過程中對全路徑進行振幅補償和相位校正，從而克服了反Q濾波方法的局限性；張平等[4]運用譜元法，對地震波在各向異性粘彈性介質中的傳播進行了波場模擬以及分析；孟凡順等[5]推導了二維非均勻黏滯性介質中地震波傳播的二階顯示差分格式，并實現了對任意復雜地質體黏滯性波場進行的正演模擬。此外，為了提高計算效率，王德利等[6]使用MPI進行三維標準線性體波動方程有限差分并行數值模擬。

近年來，基于常Q模型，有一種包含非整數階的波動方程被提出[7]。有研究表明，分數階波動方程能更好地刻畫地震波在粘彈性介質中的衰減和頻散過程[8]。Carcione[9-10]采用Grunwald-Letnikov逼近方法近似求解時間分數階波動方程，實現了粘滯聲波和彈性波的波場模擬。然而，計算時間分數階偏導數需要使用當前時刻以前所有時刻所對應的波場值，這會導致巨大的內存需求。為了解決這一問題，Carcione[11]又將時間偏導數轉換為分數階拉普拉斯算子，該算子可以通過快速傅里葉變換進行計算。這種算法避免了對當前時刻以前所有波場值進行存儲這一問題，同時數值計算也大為簡化。在此基礎上，Zhu等[12]推導了基于解耦拉普拉斯算子的粘滯波動方程。解耦的拉普拉斯算子含有兩項，其中一項表征振幅衰減，另外一項表征相位錯動。該解耦的拉普拉斯算子應用于逆時偏移(RTM)時，只需將表征振幅衰減的一項取負號，而保持表征相位錯動一項符號不變即可同時實現振幅的補償和相位的校正。最近Zhu等[13- 14]、Wang等[15]、吳玉等[16]發展了基于這種解耦的分數階方程的逆時偏移方法,并取得了理想的偏移結果。

然而解耦的分數階方程在數值求解時存在一定的困難。因為該分數階的階數是與Q 有關的隨空間變化的的函數，所以分數階的拉普拉斯算子就是關于波數和空間的混合算子，而這個混合域的算子是不能直接進行傅里葉反變換的。Zhu在計算時，簡單地采用了將Q 取空間平均值的辦法，這種做法雖然解決了上述問題，但無疑會引入計算誤差。為了精確求解該分數階波動方程，Li等[17]使用最小二乘擬合的辦法來近似隨空間變化的拉普拉斯算子；Chen 等[18]、 Sun等[19]使用Low-rank近似方法將混合算子分離并獲得了較高的波場模擬精度；Yao等[20]采用Hermite分布近似函數(HDAF)來計算分數階拉普拉斯算子。HDAF方法計算時不依賴于FFT，因此相比于其他方法，具有更好的靈活性和并行性。此外，Chen等還提出了一種基于泰勒展開的方法來近似混合域的拉普拉斯算子，相比于其他方法，這種基于泰勒展開的方法計算量更小，同時具有較高的波場模擬精度。

上述方法都基于分數階粘滯聲波方程，彈性波方程相比于聲波方程計算更復雜，但其包含的波場信息也更為豐富。因此，發展分數階解耦的粘滯彈性波動方程是具有實際意義的。筆者從Zhu所提出的分數階彈性波動方程出發，利用泰勒近似的方法分離混合域的拉普拉斯算子，最終推導出一組階數固定的分數階粘滯彈性波動方程，從而有效地避免了變分數階拉普拉斯算子的混合域求解問題。本文所提出的方程只包含速度-應力兩個分量，而Zhu的方程包含應力-應變-速度三個分量。因此我們的方程計算簡單，內存占用小更小。另外，筆者采用偽譜法計算分數階拉普拉斯算子，可以有效地避免空間頻散問題。

1 方法原理

一階速度-應力分數階粘滯彈性波動方程可以表示為:

(1)

且

(2)

式中：σxx、σxz和σzz表示應力分量;vx和vz表示速度分量;ρ代表密度;cop以及cos為在參考頻率為ω0時的P波和 S波的速度;fx和fz為震源的水平和垂直分量。ηp與ηs為方程中主控相位的參數，τp與τs為方程中主控振幅的參數；Mo和μo分別為P波和 S波的模量；γp,s為分數階的階數，由其定義可知，γp,s與空間可變的品質因子Qp,s有關。對于非均勻介質，Zhu采用的取平均值確定γp,s的做法顯然會引入計算誤差。下面將介紹一種更加準確的近似方法。

以式(1)中的第三項為例，假設介質均勻，使用廣義傅里葉偽譜方法將其變換到波數域，可以得到如下表達式：

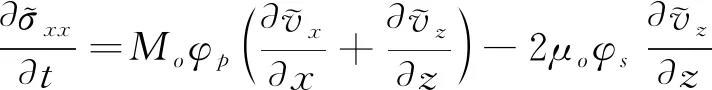
(3)

且

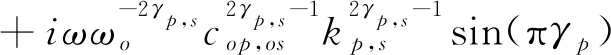
(4)

(5)

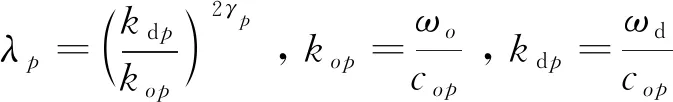
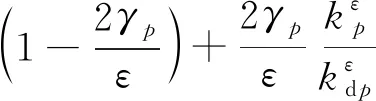
(6)

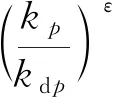
類似地，方程(1)中的其他項也可以運用上述的方法進行近似，最終推導出新的解耦的分數階粘滯彈性波方程：

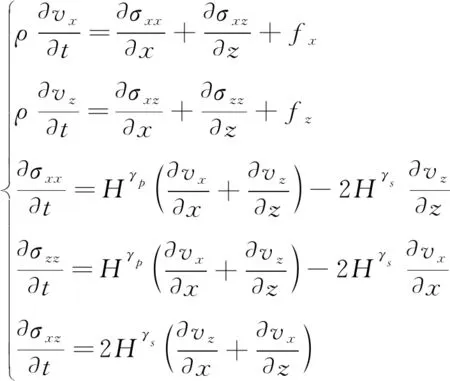
(7)

以及，

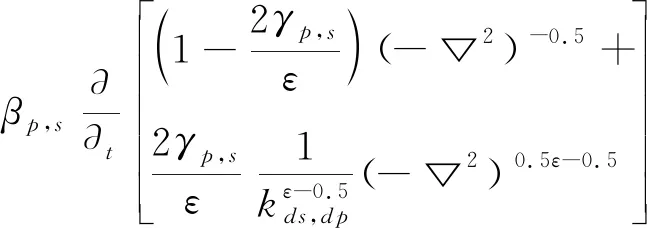
(8)

其中，

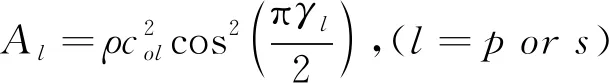
(9)

對比方程(1)與方程(7)和方程(8)可以發現，我們推導的新的分數階方程的階數是常數，從而避免了階數隨空間變化的原方程的求解誤差。

2 實驗結果

2.1 層狀模型

首先考慮一個簡單的雙層介質模型，模型的介質參數如下：上層介質縱波速度為3 000 m/s，橫波速度為2 200 m/s，縱橫波的品質因子都取為20；下層介質縱波速度為4 000 m/s，橫波速度為3 200 m/s，縱橫波的品質因子都取為100。理論上，橫波的品質因子應該小于縱波品質因子，但為了簡便，設置為二者相同。模型尺寸為400×400個網格點，空間采樣間隔為10 m，時間步長為1 ms。水平界面位于深度為2 200 m處。主頻為25 Hz的雷克子波震源位于模型中心。對于該模型，我們采用三種方法進行求解：Zhu的平均求解方法(方程(1))，本文提出的方法(方程(7)和方程(8))，以及Point-wise求解方法。Point-wise方法即為對該層狀模型的上、下兩部分分別求取分數階的拉普拉斯算子，該方法是精確的，可作為參考解。但是由于該方法需要對每一塊參數均勻的區域進行計算，當模型復雜時，Point-wise求解方法將面臨巨大的計算開銷。圖1展示的波場快照中：圖1(a)是采用Zhu的平均方法，圖1(b)是采用本文提出的方法，圖1(c)是采用Point-wise方法，圖1(d)是圖1(a)與圖1(c)的差異，圖1(e)是圖1(b)與圖1(c)的差異，圖1(f)是使用完全彈性波動方程模擬該模型的結果。所有圖片都顯示在同一色標范圍內。由圖1可見：①Zhu的平均求解方法與參考解之間存在較大誤差，本文提出的方法與參考解之間的誤差則很小；②相比于完全彈性方程，粘滯波動方程模擬的振幅存在明顯衰減。

為了進一步對比，圖2顯示了距離震源1 km處的單道地震記錄。由圖2可見：①相比于完全彈性方程，吸收衰減介質不僅造成了地震波振幅的衰減，同時也造成了相位的畸變；②與參考解相比，Zhu的平均求解方法同時造成振幅和相位都存在誤差，而本文提出的方法則很好地匹配了參考解。

圖1 不同方法計算得到的波場快照及其差值Fig.1 Snapshots computed by different methods and their residuals(a)平均方法；(b)本文方法；(c)參考解；(d)為(a)與(c)的差值；(e)為(b)與(c)的差值；(f)完全彈性介質的波場快照

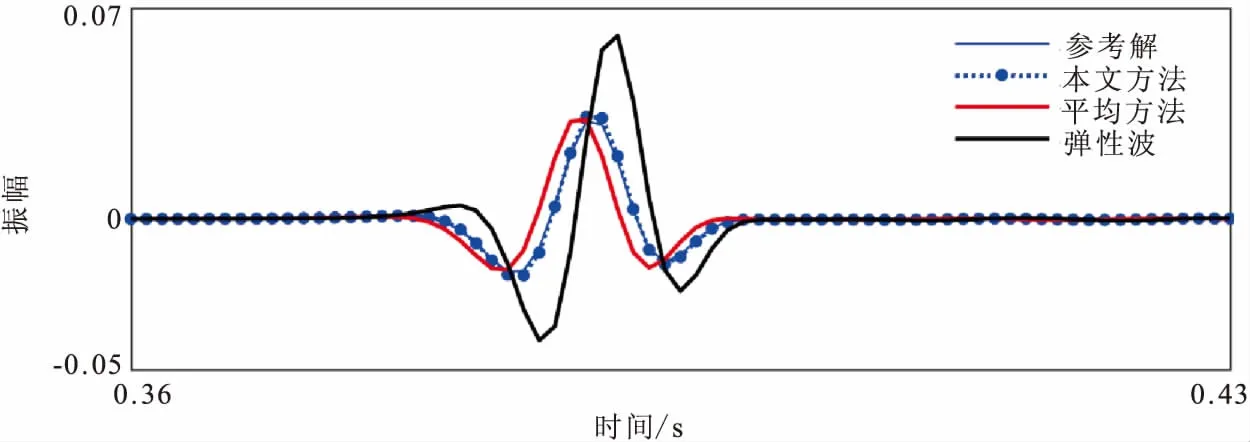
圖2 雙層介質1 km處單道地震記錄對比Fig.2 Traces computed by different methods of two-layer model at 1 km

圖3 BP模型Fig.3 BP model(a)P波速度；(b)P波品質因子

2.2 復雜模型

圖3展示的是經典的BP氣云模型，圖3(a)為P波速度Vp模型，S波速度由Vs=Vp/1.73 換算得到；圖3(b)為P波品質因子Qp模型，S波品質因子由Qs=Qp/1.3 換算得到。采用主頻為20 Hz的雷克子波震源，于(x,z)=(2 000 m，10 m)處激發，空間采樣間隔為10 m，時間步長為1 ms。由于該模型比較復雜，上述的Point-wise方法則不再使用，這里使用Low-rank分解方法[21]直接對方程(1)進行計算，并取較小的時間步長0.2 ms，將其模擬結果作為參考解。

圖4中：圖4(a)為Zhu的平均求解方法(方程(1))，圖4(b)為本文提出的方法，以及圖4(c)Low-rank方法模擬的單炮記錄。圖5則是對應的(x,z)=(1 500 m，10 m)處的地震記錄，由圖4、圖5可以發現，對于非均勻介質，平均方法求解的地震記錄與參考解之間存在較為明顯的誤差；而本文提出的新的解耦分數階粘滯波動方程的模擬結果幾乎與參考解完全吻合。

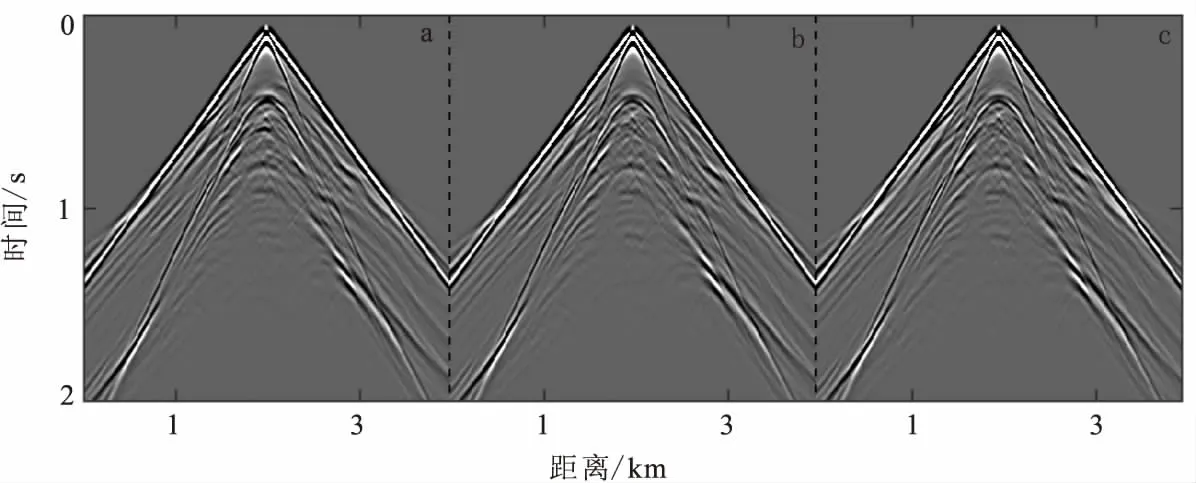
圖4 不同方法計算得到的單炮記錄Fig.4 The common-shot gathers calculated by different methods(a)平均方法；(b)本文方法；(c)Low-rank方法(參考解)

圖5 BP模型1 km處單道地震記錄對比Fig.5 Traces computed by different methods of BP model at 1 km

3 結論

筆者在基于常Q模型的解耦分數階粘滯彈性波動方程基礎上，推導了更加適合于非均勻介質模擬的固定分數階的解耦粘滯彈性波方程。該方程中的拉普拉斯算子的階數是固定的，從而避免了由于平均階數方法引入的數值誤差。通過數值算例已經說明，無論對于簡單的層狀模型還是復雜的BP模型，本文推導的新方程都具有較好的精度。同時，本文的一階方程中，只包含速度-應力兩個分量，因此占用更小的內存開銷。該方程利用交錯網格偽譜法求解，可以有效地避免空間數值頻散。本文發展的固定分數階的解耦粘滯彈性波方程，可用于粘彈性介質的衰減補償逆時偏移。