“雞兔同籠”問題

徐仁義

摘 要：“雞兔同籠”作為經典名題，在小學三至六年級有層次地被學習。根據學生身心發展特點巧用列表法、畫圖法、假設法和列方程等方法進行解決，有效地滲透并發展了學生數形結合、化歸枚舉、代數等數學思想方法，促進了學生數學素養的提升。

關鍵詞：雞兔同籠;數學思想;建模

中圖分類號：G623.5 文獻標識碼：A 收稿日期：2019-01-20 文章編號：1674-120X（2019）15-0060-02

“雞兔同籠”是我國古代非常有名的趣題，最早記載于《孫子算經》中。當下，雞兔同籠問題已經編入數學課本。如何讓學生真正掌握雞兔同籠問題的解題方法，從而培養學生的數學思維和數學思想呢？

一、教材解讀

“雞兔同籠”作為經典名題，在各版教材中都有編排，其目的是“介紹一些比較著名的數學問題，讓學生在解決這些問題的過程中，能主動嘗試從數學的角度尋找解決問題的策略，在經歷猜想、實驗、推理等數學探索的過程中滲透數學思想方法，培養學生解決問題的實踐經驗和能力，激發學生對數學的好奇心和求知欲”。（摘自《義務教育數學課程標準（2011年版）》）

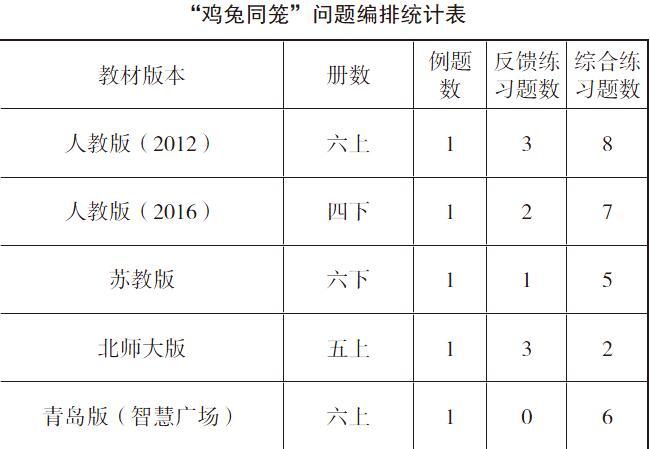
筆者對各版本教材有關雞兔同籠問題的內容進行了研讀，并統計成下表：

蘇教版六年級下冊將它作為一題練習題來鞏固“假設和替換”的策略;北師大版五年級上冊“嘗試與猜測”中用它來讓學生學會表格列舉;而人教版更是濃墨重彩，從原來的六上調整到四下，教學要求也有所改變。六上要求學生掌握列表法、假設法、方程等方法，同時也蘊含著豐富的思想方法：化歸、枚舉、數形結合、方程、建模等。四年級只需要掌握列表調整和假設法，其他方法不涉及。對四年級學生而言，經歷猜測、嘗試、調整的過程，培養有序思考的習慣、體驗假設思想、積累學習經驗才是最重要的。

二、教學策略

人教版教材將“雞兔同籠”安排在四年級，其實它可以放在三至六年級進行學習，體現層次性和系統性。

（一）三年級：巧用數形結合來表征

三年級學生初次接觸“雞兔同籠”問題，受所學知識的局限，如同一個手無寸鐵的小孩面對高大猙獰的“猛獸”，感到無助和害怕。要想戰勝它，只有通過數形結合，運用觀察、比對的思想方法，才能找到解決問題的突破口。

【例1】養殖場，養了雞、兔共8只，腳共有22只，問養殖場有雞、兔各多少只？

1.表格法

學生根據雞、兔共8只，可以得到下表：

再根據表中雞和兔的具體數量分別計算出每種情況腳的總數，最后根據腳的總數比較得到雞5只、兔3只。

采用表格法解題，優點在于便于學生理解思路，掌握方法;缺點是當數量較大時，計算麻煩。

2.畫圖法

用8個小圓圈表示8個動物的頭（如圖1）。

兩種動物混在一起，每種動物的腳數又不同，三年級學生思考起來比較復雜。為了將問題簡單化，先假設只有一種動物，假設都是雞，就在每個圓圈下面畫上2只腳（如圖2）。

假設：假設都是雞，雞的腳數一共：8×2=16（只）。

比較：與實際的22只腳相比少：22-16=6（只）。

找原因：把兔錯當成了雞，每只兔錯當成雞，就少算4-2=2（只）。

調整：把兔少算的2只腳補上去。每只雞補上2只腳就成了兔。

列式計算：兔的只數=相差總數÷每只相差數=6÷2=

3（只）（如圖3）。

學生借助作圖法解題，自主探索到“假設法”解題的思維過程。就這樣，學生運用圖表直觀地表征了各種思想方法，經歷了從“圖表化”到“數學化”逐步抽象的過程，把復雜的數學問題變得簡潔而形象。

（二）四年級：巧用假設法來突破

學生初步感知了數形結合的解題方法后，面對“雞兔同籠”，再也沒有了“小孩面對猛獸”時的窘狀，倒像是手拿武器的戰士，充滿自信前去勇斗。四年級學生主要學習運用比較和分類、分析和綜合等思想方法，掌握用假設法解決“雞兔同籠”問題的基本方法。

【例2】某養殖場，養了雞、兔共35只，雞的腳比兔的腳多22只。問雞、兔各多少只？

方法一：假設都是雞

（1）假設：雞腳比兔腳多：35×2-0×4=70（只）。

（2）比較：與實際的多22只腳相比相差：70-22=48（只）。

（3）找原因：把兔錯當成了雞，每只兔錯當成雞，就少算4+2=6（只）。

（4）調整：48里面包含幾個6，就是兔的只數。

（5）列式計算：

兔：（70-22） ÷（2+4）=8（只），雞：35-8=27（只）。

方法二：假設都是兔

雞：（35×4+22）÷（4+2）=162÷6=27（只）。

兔：35-27=8（只）

（三）五年級：活用假設法來拓展

通過四年級的學習，學生發現解決“雞兔同籠”問題不僅僅只有“假設法”，而 “假設法”也不是只能解答“雞兔同籠”。這好比一個剛從迷宮出來的人，突然覺得天地豁然開闊，感受到生活中很多問題，都能用“假設法”解決。

【例3】數學競賽中，有12道計算題，評分規定：每答對一道題得10分， 答錯一道題要倒扣 4 分。丁丁答了全部題目，但最后只得了50分，他答錯幾題？

思考：把什么類比成總頭數？把什么類比成總腳數？把什么類比成雞、兔的腳數？

方法一：假設都答對

答錯題數：（12×10-50）÷（10+4）=70÷14=5（題）。

方法二：假設都答錯

答對題數：（50+12×4）÷（10+4）=98÷14=7（題）。