《九章算術》勾股章及其劉徽注中的變式思想①

齊春燕 汪曉勤

(1. 嶺南師范學院數學與統計學院 524048; 2.華東師范大學教師教育學院 200062)

眾所周知，變式教學是我國傳統的教學方式.在教學過程中，教師在保持概念、公式、定理、圖形等的本質屬性不變的前提下，通過改變概念的表述方式、變換問題的條件和試題的內容和形式、改變圖形的形狀、位置和大小等在不變中求變，在變中求不變，引導在求異、思變中創新，以培養學生良好的創造性思維品質和創造性學習的能力.鮑建生等認為，用于構建特定經驗系統的變式，通常來自問題解決的三種拓展[1]：(1)一題多變；(2)一題多解；(3)一法多用.

變式思想并非現代教育的產物.沈康身先生在介紹中算家的“教學思想”時，曾簡要提及一題多解方面的工作[2].本文對《九章算術》勾股章及其劉徽注進行深入分析，試圖較全面地揭示其中的變式思想，以拓展教育取向的數學史研究的內涵.

1 《九章算術》勾股章的內容

《九章算術》是我國最重要的數學經典之一，書中包含246個問題，這些問題可分為九類，形成九章.其中，勾股章專門討論有關直角三角形問題，含24問，由三部分組成.第1-13問為勾股定理的應用題，具體內容是已知a,b,c,a+b,b+c,a+c,b-a,c-a,c-b中的兩個元素，求其他元素；第15-20，22-24問為相似直角三角形的應用題，包括勾股容方、勾股容圓以及其他測量問題；第14和21兩問為勾股數問題.

設a,b,c分別為(小)直角三角形的勾、股、弦，d為直角三角形內接正方形的邊長，x,y分別為直角三角形內接長方形的長和寬，D為直角三角形內切圓的直徑，24個問題[3]的相關信息見表1.

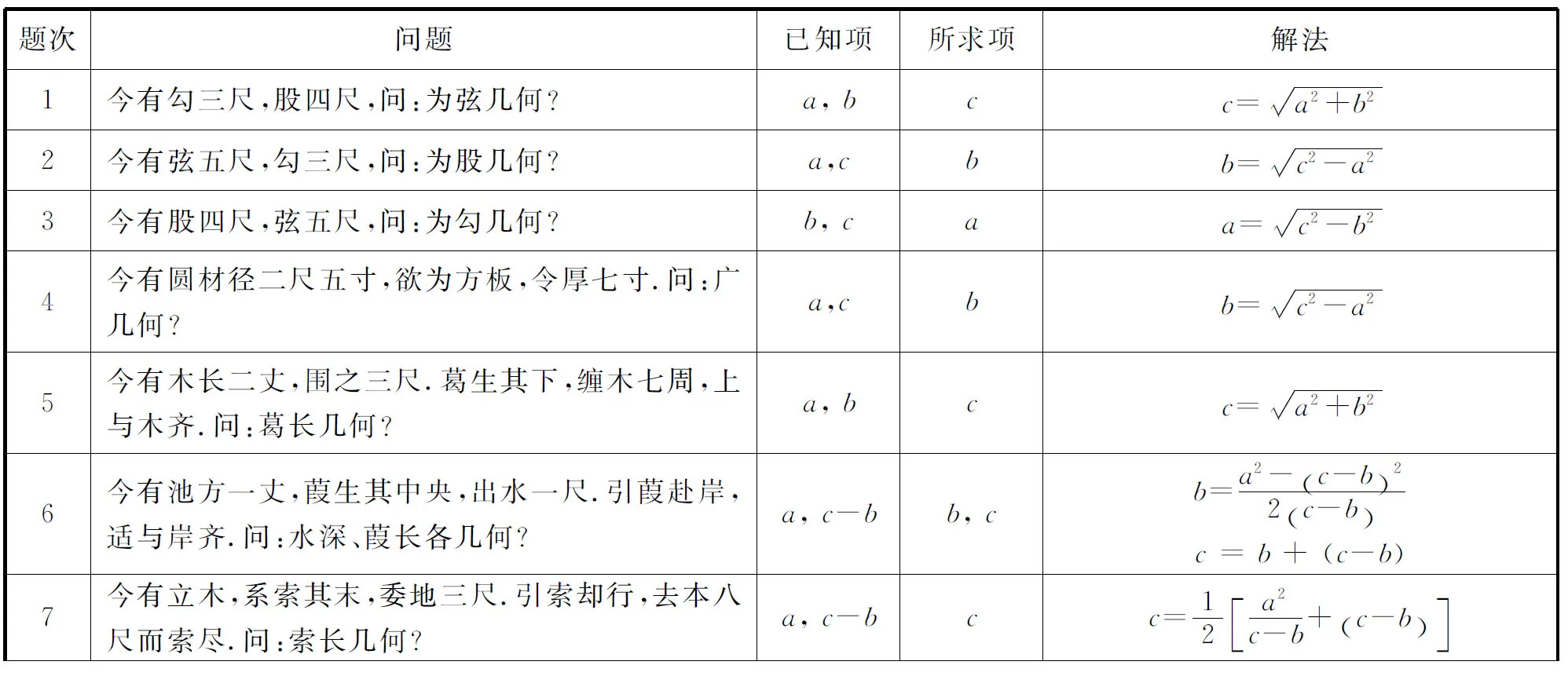
表1 24個問題相關信息表

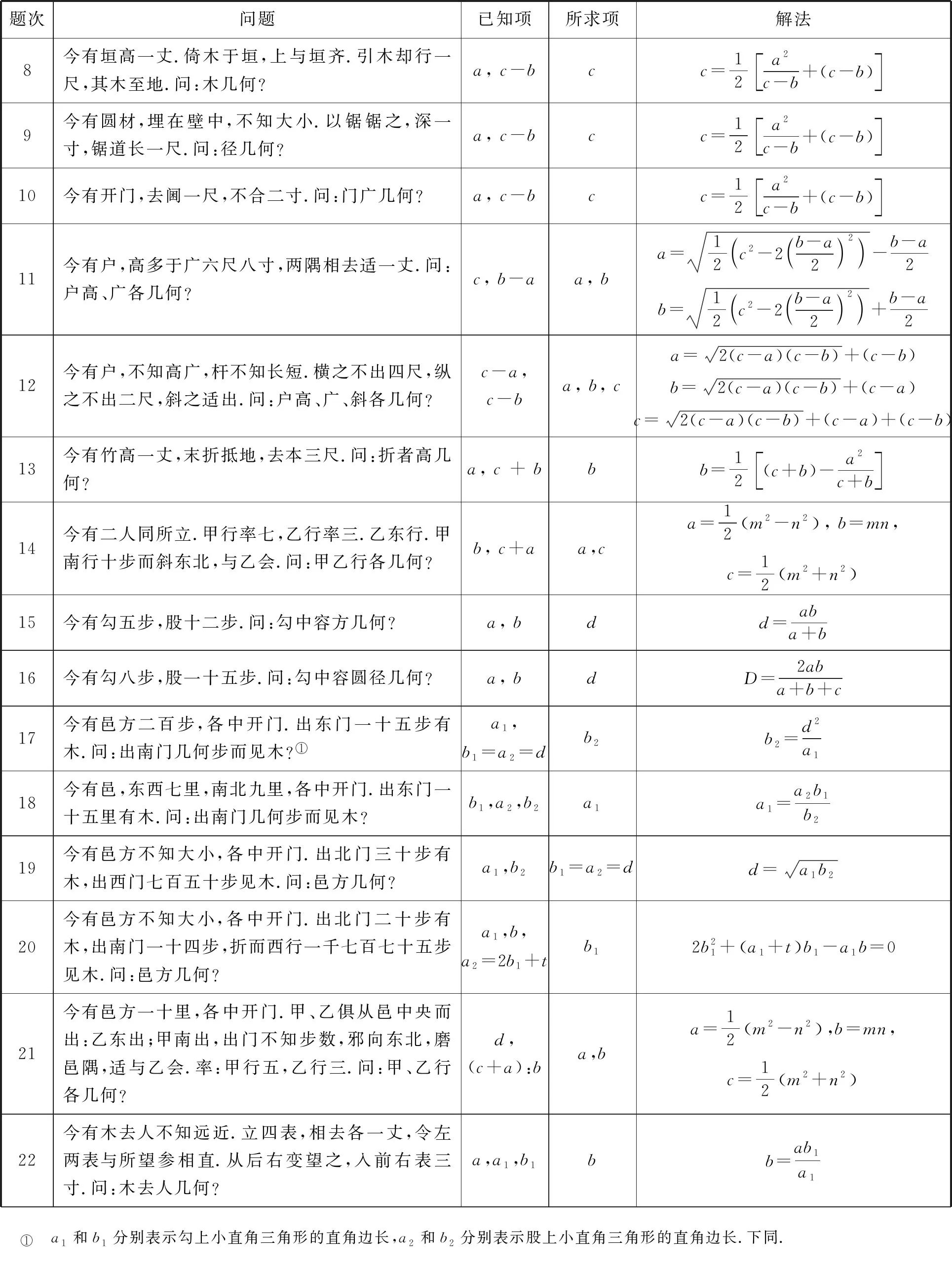
續表

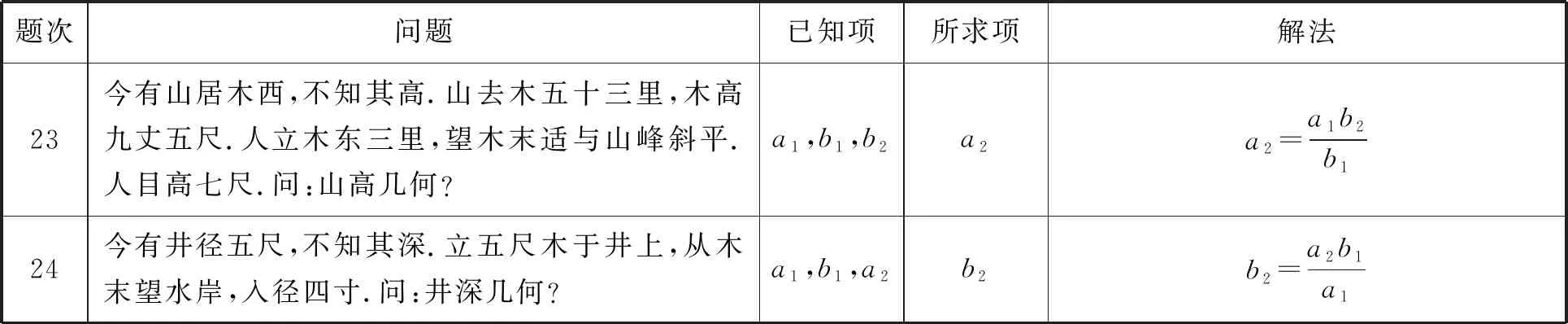
續表

2 一題多變

一題多變是題目結構的變式，通過改變題目的條件或目標，從不同角度、不同方面揭示題目的實質.美國學者希爾佛(Silver)等人[4][5]的研究表明，根據已有問題提出新問題的具體策略有四種：

(1)條件操作，即改變現有問題的已知條件，而保持所求目標不變；

(2)目標操作，即改變現有問題的所求目標，而保持已知條件不變；

(3)對稱互換，即將現有問題的條件和目標互換；

(4)新舊鏈接，即以現有問題的目標為條件，提出新問題.

表2給出基于勾股章第1題提出新問題的具體例子.

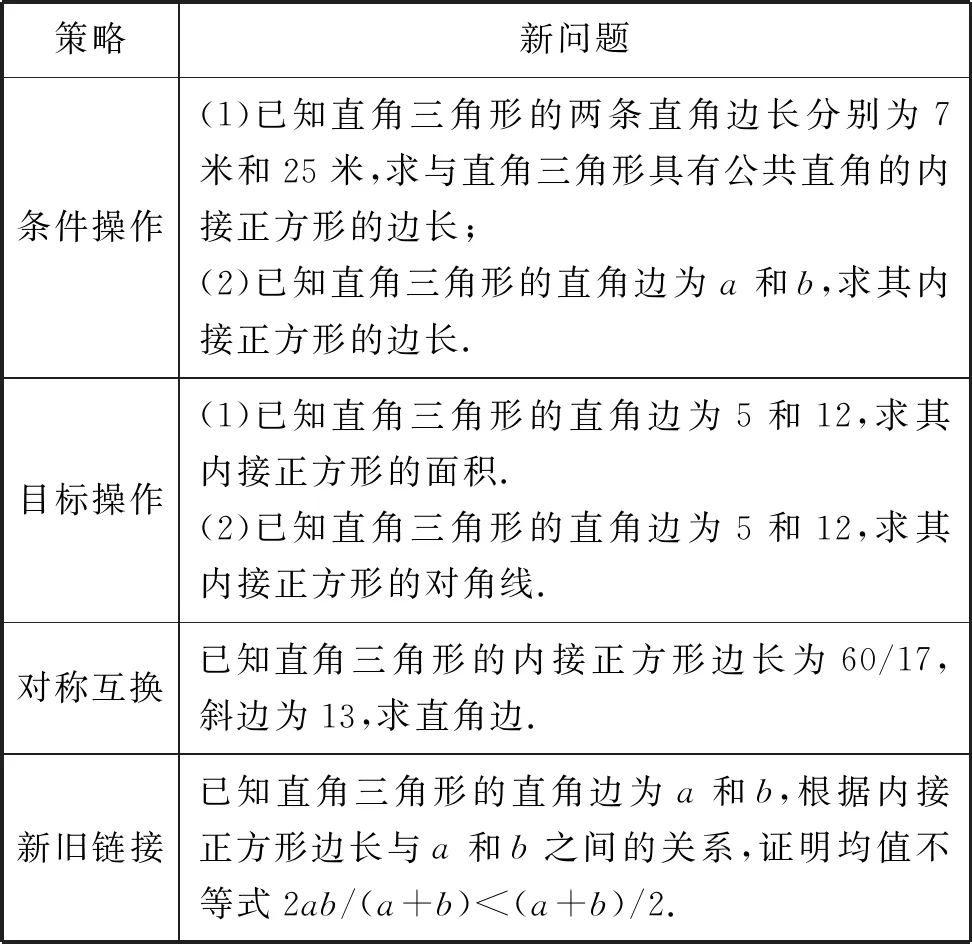
表2 基于勾股章第1題的問題提出舉例

其中，條件式策略包括兩種情形：(1)改變已知條件中的具體數據，我們稱之為條件操作Ⅰ；(2)改變已知條件的類型，稱為條件操作Ⅱ.如在直角三角形ABC中，將條件a=5，b=12改成a=8，b=15，即為條件操作Ⅰ；將條件a，b改為a，c-b或c-a,b，但保持目標不變，則為條件操作Ⅱ.如果數據和類型都改變，則仍歸為條件操作Ⅱ.

圖1給出了勾股章諸問題之間的關系.從圖中可見，問題1是所有24個問題的出發點.從該問題出發，通過條件操作Ⅰ得到問題5，通過對稱互換分別得到問題2和3.從問題3出發，通過條件操作Ⅱ，得到問題11.從問題2出發，通過條件操作Ⅰ和Ⅱ，分別得到問題4、6和13.從問題13出發，通過對稱互換，得到問題14.從問題6出發，通過條件操作Ⅰ，得到問題7-10，各問題通過條件操作Ⅱ，得到問題12.

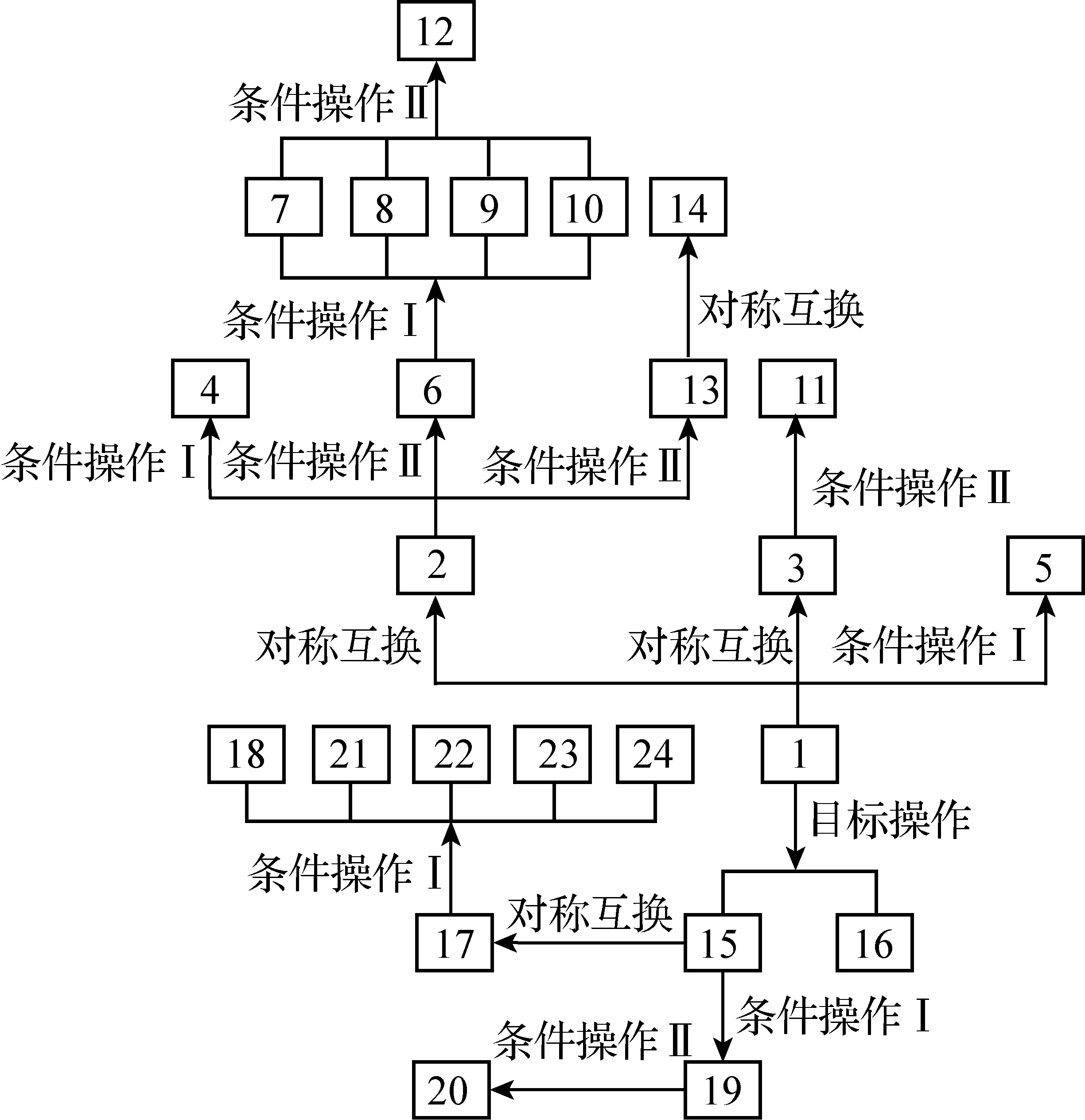
圖1 勾股章諸問題之間的聯系

從問題1出發，通過目標操作，得到問題15和16.從問題15出發，通過條件操作Ⅰ，得到問題19.從問題19出發，通過條件操作Ⅱ，得到問題20.從問題15出發，通過對稱互換，得到問題17.從問題17出發，通過條件操作Ⅱ，得到問題18，21-24.

另一方面，雖然從問題1出發，通過目標操作得到問題16，但問題16的解決是建立在勾股定理基礎上的，因為直角三角形內切圓直徑需要用直角邊和斜邊共同來表達.也就是說，從問題1到問題16，也隱含了新舊鏈接的策略.

由此可見，希爾佛等所總結的四種問題提出策略并非現代人的創造，而是早已為《九章算術》的編撰者所用.

3一題多解

三國時期數學家劉徽在注釋《九章算術》時十分重視一題多解，典型的例子是勾股容方和勾股容圓公式的推導.

3.1 勾股容方公式

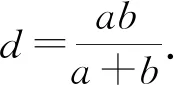
方法1：割補法

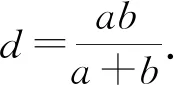
圖2

圖3

方法2：比例法

如圖4，設勾上小直角三角形的直角邊長為a1和b1，股上小直角三角形的直角邊長為a2和b2，則因a:b=a1:b1，故(a+b):b=(a1+b1):b1，但a=a1+b1,b1=d，故(a+b):b=a:d.

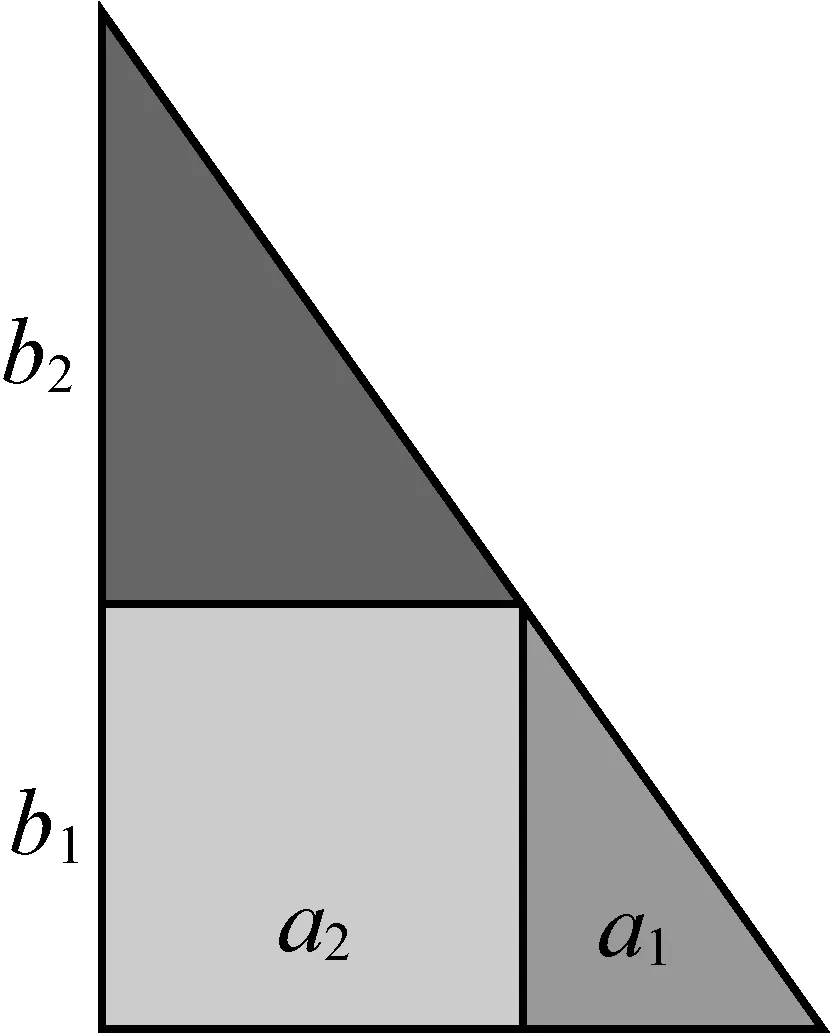
圖4

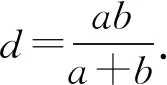
3.2 勾股容圓公式

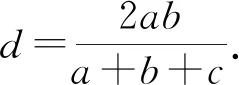
方法1：割補法

圖5

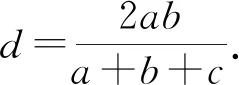
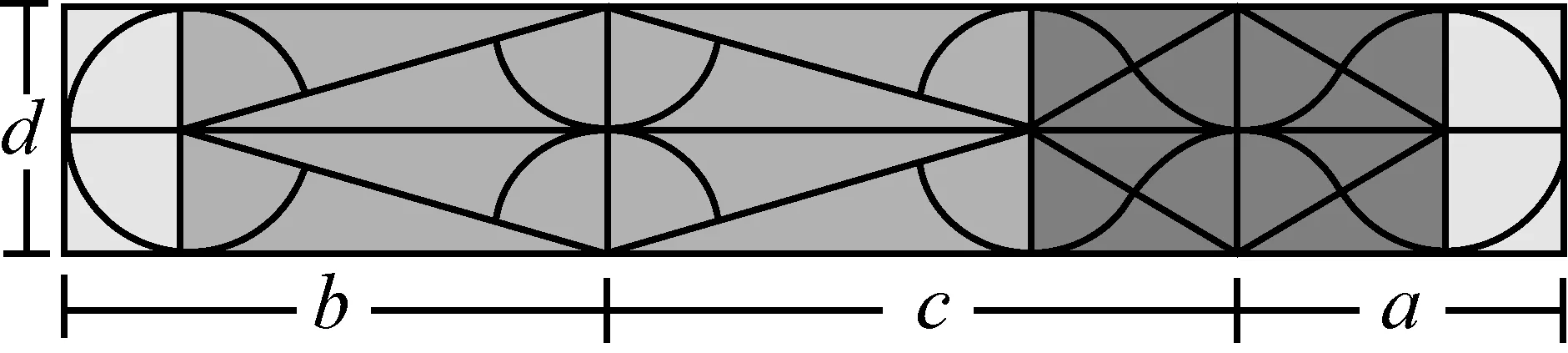
圖6

方法2：比例法

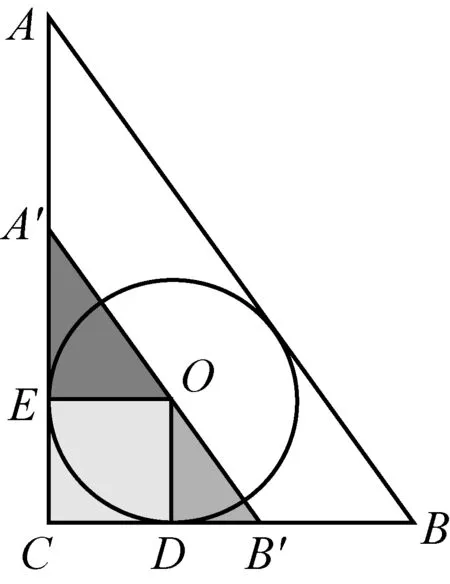
圖7

如圖7，圓O為Rt△ACB的內切圓，過圓心O作斜邊AB的平行線，分別交AC和BC于A′和B′，易證AA′=OA′，BB′=OB′.因Rt△A′EO～Rt△ACB，故有

由等比定律得

(1)

同理，由Rt△ODB′～Rt△ACB，可得

(2)

圖8

4 一法多用

勾股章第17-24問均為測量問題(表1)，這些問題都可歸結為直角三角形內接長方形問題.如圖4所示，利用勾上小直角三角形(青冪)、股上小直角三角形(朱冪)以及整個直角三角形兩兩之間的相似性，可得

(3)

故已知a1，b1，a2，b2，a和b中的三個，可求得其他未知項.第17-20、22-24諸題均通過上述方法求解.

5 結語

根據以上分析，我們得到如下結論：《九章算術》勾股章的問題是以第1題(已知勾、股求弦)為出發點，通過條件操作、目標操作和對稱互換三種策略編制而成，體現了精彩的一題多變的變式思想；所有測量問題均利用“相似直角三角形對應邊成比例”這一性質來解決，體現了一法多用的變式思想.劉徽在推導勾股容方和勾股容圓公式時采用了不同的方法，體現了一題多解的變式思想.因此，在我國，數學教育中的變式思想至遲可以上溯至《九章算術》成書的時代.

在劉徽之后，中算家們繼續運用變式思想，不斷提出和解決新的勾股問題，形成了一個獨特的課題，即“勾股算術”.因此，變式思想在我國數學教育史上歷史悠久、綿延不絕.至此，我們不難理解為什么變式教學是我國傳統的教學方式了.追溯變式思想的歷史淵源，我們也獲得了重要的啟示，一個國家或民族的數學教育特色，必定是傳承歷史的結果；只有民族的，才是世界的.