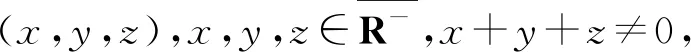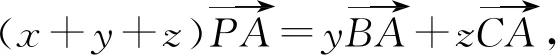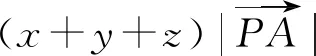Guggenheimer不等式的高次加權推廣

費紅亮,曾善鵬 ,楊學枝

(1.杭州高級中學 310003；2.杭州市電子信息職業學校 310021；3.福州市福州第二十四中學 350015)

1 問題背景

1967年，H.W.Guggenheimer建立了如下不等式，我們稱之為Guggenheimer不等式.

定理A[1].P是△ABC中任意一點，a,b,c是三角形三邊，則有

PA+PB+PC

1971年，M.S.Klamkin得到上述不等式二次形式，我們稱之為Klamkin不等式.

定理B[2].P是△ABC中任意一點，a,b,c是三角形三邊，則有

PA2+PB2+PC2

1989年，陳計對定理B進行推廣得到如下結果.

定理C[3].P是△ABC中任意一點，a,b,c是三角形三邊，n是任意正整數，則

PAn+PBn+PCn

實際上，可以得到Guggenheimer不等式和klamkin不等式的加強形式.

定理D[4][5].P是△ABC中任意一點，a,b,c是三角形三邊，若a≥b≥c，則有

PA+PB+PC

定理E[5].P是△ABC中任意一點，a,b,c是三角形三邊，若a≥b≥c，則有

PA2+PB2+PC2

2018年，曾善鵬和費紅亮老師對定理C、D進行加權推廣得到

定理F[6].P是△ABC中任意一點，a,b,c是三角形三邊，λ,u,v為任意正實數，若a≥b≥c，則有

λPA+uPB+vPC

定理G[6].P是△ABC中任意一點，a,b,c是三角形三邊，λ,u,v為任意正實數，若a≥b≥c，則有

λPA2+uPB2+vPC2

類比于定理F、G，本文對定理F進行加權推廣得到如下

命題1設△ABC三邊長為BC=a,CA=b,AB=c，且c最小，P為△ABC內部任意一點，λ,u,v為任意正實數，n∈N*，則

λPAn+uPBn+vPCn≤max{u,v}an+max{v,λ}bn.

于是，得到

=yc+zb，

下面先證明

①

應用數學歸納法證明式①.

當n=1時式①為等式；當n=2時，易證

? (yc+zb)2≤(x+y+z)(yc2+zb2)

? 2yzbc≤(x+z)yc2+(x+z)zb2，

≥2yzbc，因此上式成立，式①得證.

假設n=k時式①成立，即

當n=k+1，有

這時，只要證明

? (yck+zbk)(yc+zb)

≤(x+y+z)(yck+1+zbk+1)，

? (yck+zbk)(yc+zb)

≤(y+z)(yck+1+zbk+1)

?bkc+bck≤bk+1+ck+1，

? (bk-ck)(b-c)≥0，

上式顯然成立，故當n=k+1時，式①也成立，從而式①獲證.

同理可證另外類似兩式：

于是，要證明原命題1，只要證明

≤max{u,v}an+max{v,λ}bn.

②

式②右邊-左邊

=(x+y+z)[max{u,v}an+max{v,λ}bn]

-[(uz+vy)an+(vx+λz)bn+(λy+ux)cn]

=[(x+y+z)max{u,v}-(uz+vy)]an+[(x+y+z)max{v,λ}-(vx+λz)]bn-(λy+ux)cn

≥xmax{u,v}an+ymax{v,λ}bn-(λy+ux)cn

≥[xmax{u,v}+ymax{v,λ}-(λy+ux)]cn

≥0.

由此可知，式②成立，原命題1獲證.

根據命題1證明，容易得到以下

命題2(自創題)設△ABC三邊長為BC=a,CA=b,AB=c，且c最小，P為△ABC內部任意一點，λ,u,v為任意正實數，α≥1，則

λPAα+uPBα+vPCα≤max{u,v}aα+max{v,λ}bα.