貝葉斯統(tǒng)計分析的新工具— Stan*

劉 晉 汪秀琴 李天萍 徐文華 陳 峰

【提 要】 目的 鑒于國內(nèi)研究者熟悉的貝葉斯統(tǒng)計軟件WinBUGS已停止更新，OpenBUGS已見介紹，本文介紹國外新近出現(xiàn)的貝葉斯統(tǒng)計軟件Stan的基本原理與實際使用。方法 由于Stan安裝具有其自身特點且較為復雜，本文首先介紹Windows平臺下Stan安裝與使用方法，接著介紹Stan語言及運行步驟，最后以線性-正態(tài)層次模型為例介紹Stan的應用。結(jié)果 Stan作為一種新型貝葉斯統(tǒng)計軟件，使用了全新的漢密爾頓蒙托卡羅(Hamiltonian Monte Carlo，HMC)抽樣方法，可以處理GIBBS抽樣難以收斂的復雜多元層次模型。Stan使用的概率模型定義語言，相比較BUGS，邏輯清晰，程序更易理解。結(jié)論 Stan功能強大，應用方便，是貝葉斯分析的有力工具。

貝葉斯統(tǒng)計歷史悠久，與頻率統(tǒng)計并稱統(tǒng)計學的兩大學派。自Tomas Bayes提出貝葉斯定理至今已有300余年，直到近30年，馬爾科夫鏈-蒙托卡羅(Markov Chain Monto Carlo，MCMC)模擬技術以及計算機技術的迅速發(fā)展使計算后驗分布高維積分的難題得以解決，貝葉斯統(tǒng)計才在理論與應用上得以快速發(fā)展。各類基于MCMC的貝葉斯統(tǒng)計軟件的出現(xiàn)，將研究者從復雜繁瑣的后驗分布計算中解脫出來，從而更專注于貝葉斯模型本身，非統(tǒng)計專業(yè)人員也能將貝葉斯統(tǒng)計應用于相應領域。可以說，貝葉斯統(tǒng)計軟件對貝葉斯統(tǒng)計理論和應用的發(fā)展起到了重要作用。

目前國際上常用的貝葉斯統(tǒng)計軟件有BUGS(WinBUGS、OpenBUGS)、JAGS、Stan及多種R軟件包[1-3]。國內(nèi)對WinBUGS軟件有較為詳盡的介紹[4-9]，但該軟件已于2007年停止更新。最近對該軟件的發(fā)展版OpenBUGS已見介紹[10-13]。而Stan是近年新出現(xiàn)的貝葉斯統(tǒng)計軟件，與BUGS等貝葉斯統(tǒng)計軟件相比，Stan具有應用平臺廣、復雜模型下計算速度快、語言更加靈活的特點，在國外已受到廣泛關注。如貝葉斯統(tǒng)計的著名學者Andrew Gelman使用Stan作為其著作的例子[2]，Kruschke在其介紹貝葉斯統(tǒng)計分析的著作中將Stan作為示例軟件之一[1]。這些動向說明Stan正成為貝葉斯分析工具的新選擇，但國內(nèi)尚未見相關研究。

Stan軟件基本情況

Stan是一款基于C++語言編寫的采用MCMC方法對復雜統(tǒng)計模型進行貝葉斯推斷的專業(yè)工具。它是開源軟件，可從https://mc-stan.org/免費下載，使用者也可根據(jù)自身需求，編寫函數(shù)，擴展其功能。該軟件可在Windows、Mac OS、Linux 3種操作系統(tǒng)下運行，通過R、Python等6款統(tǒng)計軟件調(diào)用。與BUGS、JAGS主要使用Gibbs抽樣不同，Stan使用的是漢密爾頓蒙托卡羅(Hamiltonian Monte Carlo，HMC)抽樣，在復雜模型的條件下，HMC的抽樣較GIBBS抽樣效率更高。本文將以Windows環(huán)境下，使用R調(diào)用Stan為例，介紹Stan的使用方法。其它平臺以及軟件下的Stan使用方法，可以參考Stan官網(wǎng)幫助[14]。

Stan的運行可分為以下6個步驟：(1)使用Stan概率模型語言，建立貝葉斯統(tǒng)計模型；(2)通過Stanc函數(shù)將Stan模型語言編譯為C++代碼；(3)將C++代碼編譯為可以被R載入的動態(tài)鏈接庫；(4)運行動態(tài)鏈接庫的程序從后驗分布中抽樣；(5)對后驗分布樣本進行收斂診斷；(6)基于后驗分布進行統(tǒng)計推斷。

通常，(2)至(4)步可從R中調(diào)用函數(shù)來實現(xiàn)，使用者不需要了解其中具體過程，但是如需對程序進行調(diào)試，也可以逐步執(zhí)行(2)、(3)、(4)步。下文將介紹Stan軟件的安裝與具體使用過程。

Stan軟件安裝與使用

與BUGS等貝葉斯統(tǒng)計軟件相比，Stan的安裝具有其自身特點且較為復雜，本部分將介紹Windows平臺下，基于R界面的Stan安裝與使用方法。

R界面下的Stan軟件是名為RStan的R軟件包。截至本文寫作時,其最新版本是發(fā)布于2018年11月9日的2.18.2。

1.安裝

首先安裝R軟件，從https://www.r-project.org/下載，版本要求為3.4.0或更新。

RStan安裝前，為確保R中沒有RStan，在R中運行以下命令以清除原有RStan：

remove.packages("rstan")

if (file.exists(".RData")) file.remove(".RData")

重啟R，安裝rstan包。運行以下命令：

install.packages("rstan",repos="https://cloud.r-project.org/",dependencies=TRUE)

檢查C++ 工具鏈安裝情況,運行以下命令：

pkgbuild::has_build_tools(debug=TRUE)

如包含C++工具鏈的Rtools軟件尚未安裝，根據(jù)提示，從http://cran.r-project.org/bin/windows/Rtools/下載并安裝。注意在安裝過程中，需要勾選“add rtools to system Path”選項。

Rtools安裝完成后，為確認其安裝成功，重新運行命令：pkgbuild::has_build_tools(debug=TRUE)，如返回如圖1結(jié)果“TRUE”代表安裝成功。

載入rstan包，運行如下命令：library(rstan)，R顯示結(jié)果見圖2。

圖2提示運行如下三條命令以充分使用計算機CPU與內(nèi)存，保存已經(jīng)編譯的程序等，目的是加快stan程序的運行速度。這三條命令如不運行，也不影響使用。

options(mc.cores=parallel::detectCores())

rstan_options(auto_write=TRUE)

Sys.setenv(LOCAL_CPPFLAGS='-march=native')

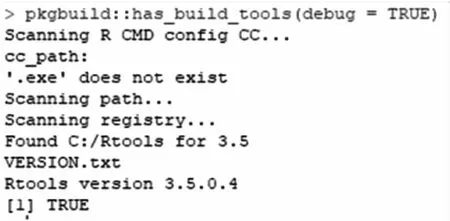
圖1 rstan安裝成功提示

圖2 rstan性能優(yōu)化配置提示

至此，rstan的安裝與配置工作結(jié)束。

2.Stan語言及應用

Stan語言是一種概率程序語言，一個完整的Stan程序一般由若干個模塊構(gòu)成，包括數(shù)據(jù)模塊(data)、參數(shù)模塊(parameters)、參數(shù)轉(zhuǎn)換模塊(transformed parameters)、模型模塊(model)、預測值模塊(generated quantities)。在各模塊內(nèi)，可以定義變量、使用賦值語句、函數(shù)以及表達式等元素。數(shù)據(jù)模塊的作用是定義構(gòu)建貝葉斯模型的觀察變量類型、取值范圍等；參數(shù)模塊定義貝葉斯模型參數(shù)的類型、取值范圍；參數(shù)轉(zhuǎn)換模塊通過表達式與賦值語句將參數(shù)模塊的參數(shù)轉(zhuǎn)換為新的參數(shù)變量；模型模塊通過對觀察變量指定特定的概率分布函數(shù)定義似然函數(shù)；預測值模塊通過變量定義與賦值語句定義預測變量。

值得指出的是，與BUGS語言不同，Stan程序是基于C++語言的，因此，各變量使用前必須定義，各模塊需按照順序排列。

以OpenBUGS軟件示例第一卷第一個例子為例[15]，部分數(shù)據(jù)示例見表 1。欲了解小鼠日齡與體重的關系。以日齡作為自變量，體重作為因變量。構(gòu)建線性-正態(tài)層次模型。

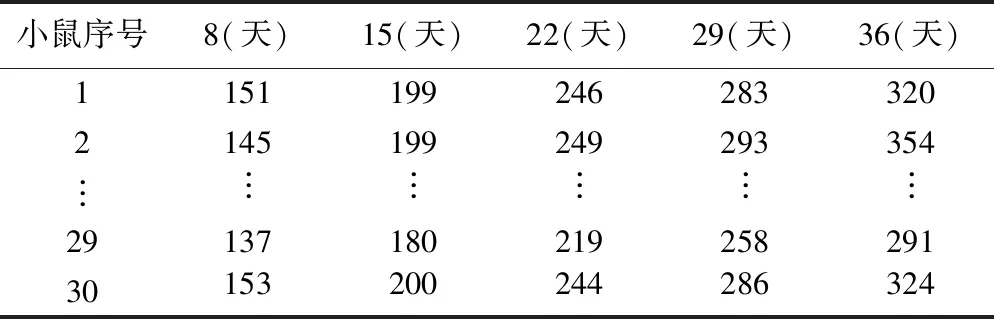
表1 小鼠成長數(shù)據(jù)示例

構(gòu)建貝葉斯模型如下：

似然函數(shù)：yij～N(ai+βi(xij-xbar),σy)

層次先驗：

第一層：αi～N(μα,σα)β～N(μβ,σβ)

第二層：σy,σs,σβ～IG(0.001,0.001),μα,μβ～N(0,100)

y代表小鼠體重，x代表小鼠日齡，下標i代表第i只小鼠，下標j代表第j天，xbar為30只小鼠5次測量體重的均值。感興趣的變量是各小鼠體重隨年齡變化的平均水平βα、基線下的小鼠平均體重α0=μα-μβxbar。

步驟1 定義Stan，構(gòu)建模型

在文本編輯器中使用Stan語法定義貝葉斯模型，以“Stan”后綴存儲，本例所用的Stan程序如下。

data {

intN;//定義總樣本量為N，類型為整數(shù)，下限為0。

intT;//定義體重測量次數(shù)為T，類型為整數(shù)，下限為0。

real x[T];//定義年齡為x，類型為實向量

real y[N,T];//定義體重為y，類型為實矩陣

real xbar;//定義體重均值為xbar,類型為實數(shù)

}

parameters {

real alpha[N];//定義參數(shù)α，類型為實向量，向量長度為N

real beta[N]; //定義參數(shù)β，類型為實向量，向量長度為N

real mu_alpha;//定義超參數(shù)μα，類型為實數(shù)

real mu_beta; // 定義超參數(shù)μβ，類型為實數(shù)

}

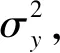
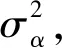
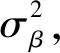
transformed parameters {

realsigma_y; //定義參數(shù)σy,類型為實數(shù)，下限為0

realsigma_alpha;//定義參數(shù)σα，類型為實數(shù)，下限為0

realsigma_beta; //定義參數(shù)σβ，類型為實數(shù)，下限為0

}

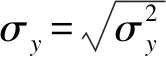
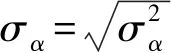
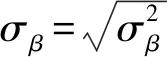
model {

mu_alpha ～ normal(0,100);//定義μα先驗分布為一扁平的正態(tài)分布

mu_beta ～ normal(0,100);//定義μβ先驗分布為一扁平的正態(tài)分布

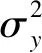
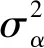
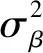
alpha ～ normal(mu_alpha,sigma_alpha); // 定義向量α的每個參數(shù)先驗分布服從正態(tài)分布

beta ～ normal(mu_beta,sigma_beta); //定義向量β的每個參數(shù)先驗分布服從正態(tài)分布

for (n in 1:N)

for (t in 1:T)

y[n,t] ～ normal(alpha[n] + beta[n]*(x[t]-xbar),sigma_y);

}//利用循環(huán)定義線性正態(tài)分布似然函數(shù)

generated quantities {

real alpha0;//定義α0類型為實數(shù)

alpha0 <- mu_alpha - xbar * mu_beta;//為α0賦值

}

本程序涵蓋了上文介紹的Stan語句模塊。結(jié)合注釋，應不難理解程序的含義。在參數(shù)模塊中指定的參數(shù)為方差，再通過參數(shù)轉(zhuǎn)換模塊將其變換為標準差，是出于提高軟件運行效率的考慮。

步驟2 數(shù)據(jù)準備

數(shù)據(jù)以R列表(list)形式存儲，其中x為小鼠的日齡，xbar為日齡均值，N為小鼠數(shù)目，T為觀察次數(shù)，y為小鼠體重。

rats_data <- list(x=c(8.0,15.0,22.0,29.0,36.0),xbar=22,N=30,T=5,y=structure(

.Data=c(151,199,246,283,320,

145,199,249,293,354,

……

137,180,219,258,291,

153,200,244,286,324),

.Dim=c(30,5)))

步驟3 后驗分布抽樣

通過library語句載入rStan軟件包，并通過Stan函數(shù)執(zhí)行HMC抽樣，結(jié)果存儲于fit_rats變量，該變量存儲了模型構(gòu)建以及后驗樣本等信息，后續(xù)的收斂診斷以及統(tǒng)計推斷的數(shù)據(jù)均來自于該變量。該變量存儲初始值、Stan函數(shù)的參數(shù)設置、Stan模型、以及后驗分布抽樣樣本等信息。執(zhí)行HMC抽樣的語句為

library(rStan)

fit_rats <- Stan(

file="C: ats.Stan",# Stan程序

data=rats_data,# 存儲數(shù)據(jù)的列表名稱

chains=4, # 馬爾科夫鏈數(shù)目

warmup=1000, # 預熱迭代次數(shù)

iter=5000 # 每條鏈的迭代次數(shù)

)

步驟4 收斂診斷

通過traceplot函數(shù)可以對估計參數(shù)繪制蹤跡圖，以對后驗樣本是否收斂進行診斷，圖3顯示了4個參數(shù)的蹤跡圖，并用灰色表示預熱狀態(tài)的抽樣。

traceplot(fit_rats,pars=c("alpha0","mu_beta","mu_alpha","sigma_y"),inc_warmup=TRUE,nrow=4)

由圖3可見，在抽樣250次后，4條馬爾科夫鏈很好的重合在一起，并保持平穩(wěn)、水平。說明模型已經(jīng)很好的收斂，更多的收斂診斷方法可以使用Stan提供的bayesplot軟件包進行收斂診斷。

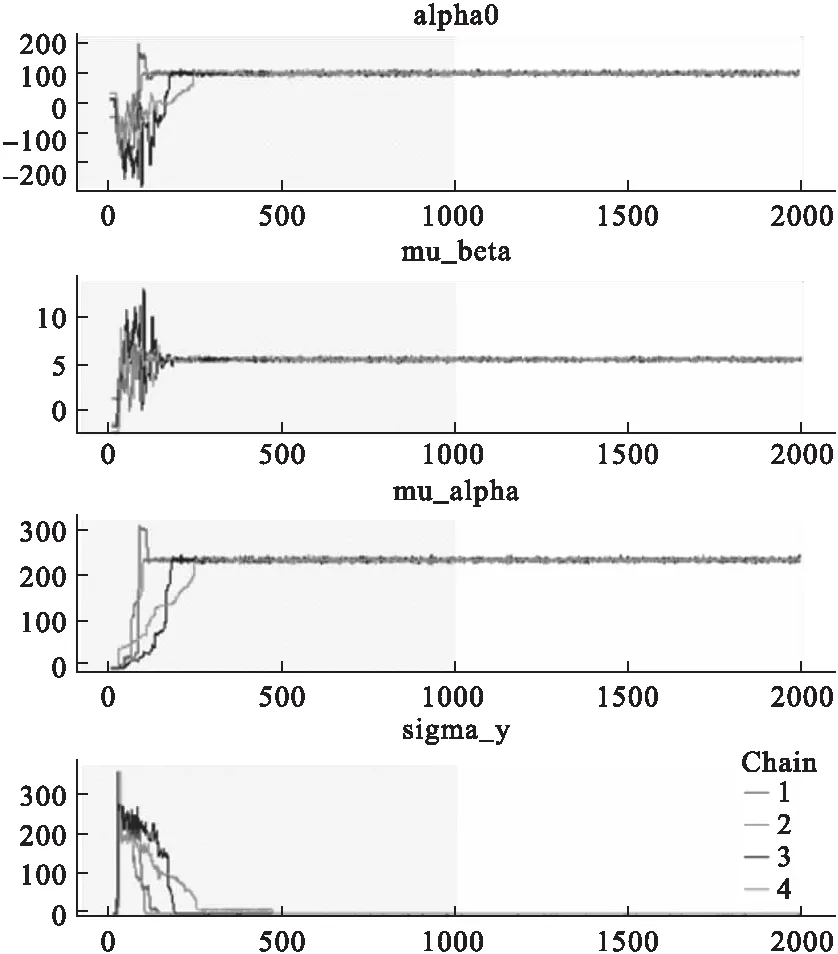
圖3 各參數(shù)后驗分布收斂情況

步驟5 后驗分布推斷

使用print 函數(shù)展示后驗樣本的統(tǒng)計推斷結(jié)果，可通過指定pars參數(shù)指定需要展示的變量參數(shù)，本例展示α0、μβ、μα、σy4個參數(shù)的后驗分布推斷結(jié)果。

print(fit_rats,pars=c("alpha0","mu_beta","mu_alpha","sigma_y"),probs=c(0.05,0.5,0.95))

討 論

本文介紹了Stan在Windows下通過R軟件進行貝葉斯統(tǒng)計建模與推斷的基本功能。該軟件也可采用其它方式調(diào)用，如命令行以及matalab、python等軟件。通過Stan_demo()函數(shù)，使用者可以利用Stan運行和BUGS相同的應用示例。同時，Stan官網(wǎng)也提供軟件詳細的說明文檔以及Stan應用的文獻。從使用便利性來講，Stan作為R的一個軟件包，與R深度融合。可以利用R軟件豐富的函數(shù)和工具包進行數(shù)據(jù)的讀取、整理以及進一步分析，極大的擴展了該軟件的功能。例如，通過ShinyStan軟件包，可以在瀏覽器界面對分析結(jié)果進行統(tǒng)計、圖形展示并提供了5種收斂診斷方法。通過Bayesplot軟件包，也可以進行收斂診斷并繪制各種圖形。通過LOO軟件包可以進行留一法交叉驗證，并計算誤差。同時，與R的結(jié)合使得Stan適合進行大規(guī)模的貝葉斯統(tǒng)計模擬。雖然OpenBUGS通過R2Bugs軟件包也可以實現(xiàn)在R中的調(diào)用，但是，它是通過外部調(diào)用實現(xiàn)的，當需要進行大規(guī)模模擬時，速度不如Stan。其次，與BUGS、JAGS等軟件相比，Stan使用了全新的HMC抽樣方法，可以處理GIBBS抽樣難以收斂的復雜多元層次模型。Stan使用的概率模型定義語言大體與BUGS類似，不同之處是，變量使用前必須事先定義，語句按順序執(zhí)行。因此與BUGS比較，則程序邏輯更為清晰，易于理解。

表2 各參數(shù)后驗推斷

當然，與BUGS相比，Stan的安裝過程略顯繁瑣，同時需要使用者掌握一定的R軟件知識。定義模型未提供圖形化的操作界面，也不能以BUGS軟件有向圖的方式定義貝葉斯模型。但總體而言，安裝與掌握該軟件的使用難度并不大，同時其官網(wǎng)提供了詳細的文字與視頻教程，以及豐富的應用實例，對于BUGS軟件的實例，均有對應的例子提供。相信初學者通過學習這些資料，可以很快掌握該軟件的使用方法。通過本文的介紹，希望能夠推動Stan軟件在國內(nèi)的應用，利用Stan軟件的強大功能，使貝葉斯統(tǒng)計在醫(yī)學研究中發(fā)揮更大作用。