基于李雅普諾夫直接法的電液力控制系統穩定性研究

陳帥杰，金曉宏,2，黃 浩,2，張邵峰

(1.武漢科技大學冶金裝備及其控制教育部重點實驗室，湖北 武漢，430081；2.武漢科技大學機械傳動與制造工程湖北省重點實驗室，湖北 武漢，430081)

電液力控制系統具有控制精度高、承載能力強、響應速度快等優點[1]，被廣泛應用于負載模擬器、材料疲勞試驗機、機器人、飛行器等設備。電液力控制系統又是一種典型的非線性系統，其傳遞函數的分子中存在振蕩頻率較低的二階微分環節[2]，因此在實際應用中易處于不穩定狀態，即使系統受到穩定約束，其性能和響應速度也很有可能降低。

研究人員在力控制系統的穩定性和精度控制方面做了大量工作。例如，徐敬廣等[3]在電液力控制系統的前向通道串聯兩個相同的慣性環節進行系統校正，并分析了系統的穩定性。Truong等[4]將基于定量反饋理論的在線可調力控制器應用于負載模擬器，提高了系統的穩定性和抗干擾能力。Li等[5]針對電機驅動的空氣動力負載模擬器中存在非線性摩擦力、受執行器的主動運動擾動和參數不確定性這三個問題，提出一種結合神經網絡和并聯分布補償的魯棒控制器策略，以保證整個閉環系統的穩定性和跟蹤精度。趙慧等[6]設計出基于線性矩陣不等式的H∞控制器，提高了電液力系統的頻寬，并使系統具有較快的響應速度和較高的穩態精度。Guo等[7]提出一種基于迭代學習機制的輸出反饋動態面控制方法，通過幾次迭代來優化電液力控制系統的期望軌跡，使輸出力收斂到目標曲線，同時還使用李雅普諾夫方法分析了閉環系統的穩定性。Shen等[8]所設計的混合控制器結合前饋補償和在線自適應逆控制的優點，提高了電液力系統的穩定性，擴展了頻率帶寬，改善了系統動態特性。上述研究使用先進的控制方法，取得了良好的控制效果，但這些高級控制算法一般比較復雜，在工程應用中難以實現。

本文所研究的電液力控制系統是為了給含有負值彈性剛度負載的位置系統實施加載，負載彈性剛度的變化對系統的穩定性、動態剛度以及穩態精度等會造成不利影響。為此，筆者從能量耗散角度出發，采用基于李雅普諾夫穩定性理論的設計方法對電液力控制系統進行穩定性分析，通過系統的閉環傳遞函數整理出關于液壓缸輸出力的三階非線性方程，利用李雅普諾夫直接法的反演方式求解系統穩定的相關條件，并且根據此條件構造出相應的物理結構補償模型，來抵消或者削弱不穩定因素對系統的影響，提高系統品質。同時，文中還比較了分別采用物理結構補償與傳統雙慣性環節校正時系統的穩定性及動態特性。

1 電液力控制系統的基本原理

圖1所示為電液力控制系統的工作原理圖。系統主要由伺服放大器、電液伺服閥、液壓缸和力傳感器構成。在指令電壓信號ur作用下，電液伺服閥輸出負載流量進入液壓缸，其進油腔壓力為p1，排油腔壓力為p2，液壓缸兩腔產生與指令信號成比例的壓力差pLp1-p2；在pL的作用下，液壓缸通過活塞桿將輸出力Fg=pLA作用在被控對象上；壓力傳感器將檢測到的輸出力的實測值Fg轉換為電壓信號uf，經反相后反饋到指令端，通過與指令信號ur比較，得出偏差信號ue，實現閉環控制。

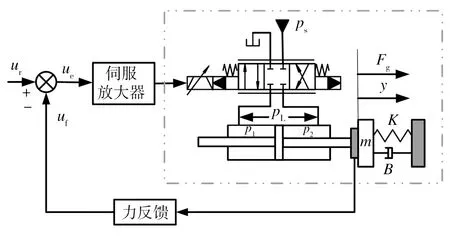
圖1 電液力控制系統工作原理示意圖

Fig.1 Schematic diagram of working principle of electro-hydraulic force control system

2 電液力控制系統的數學模型

根據文獻[9]中電液力控制系統各環節的數學方程繪制系統控制框圖，如圖2所示。

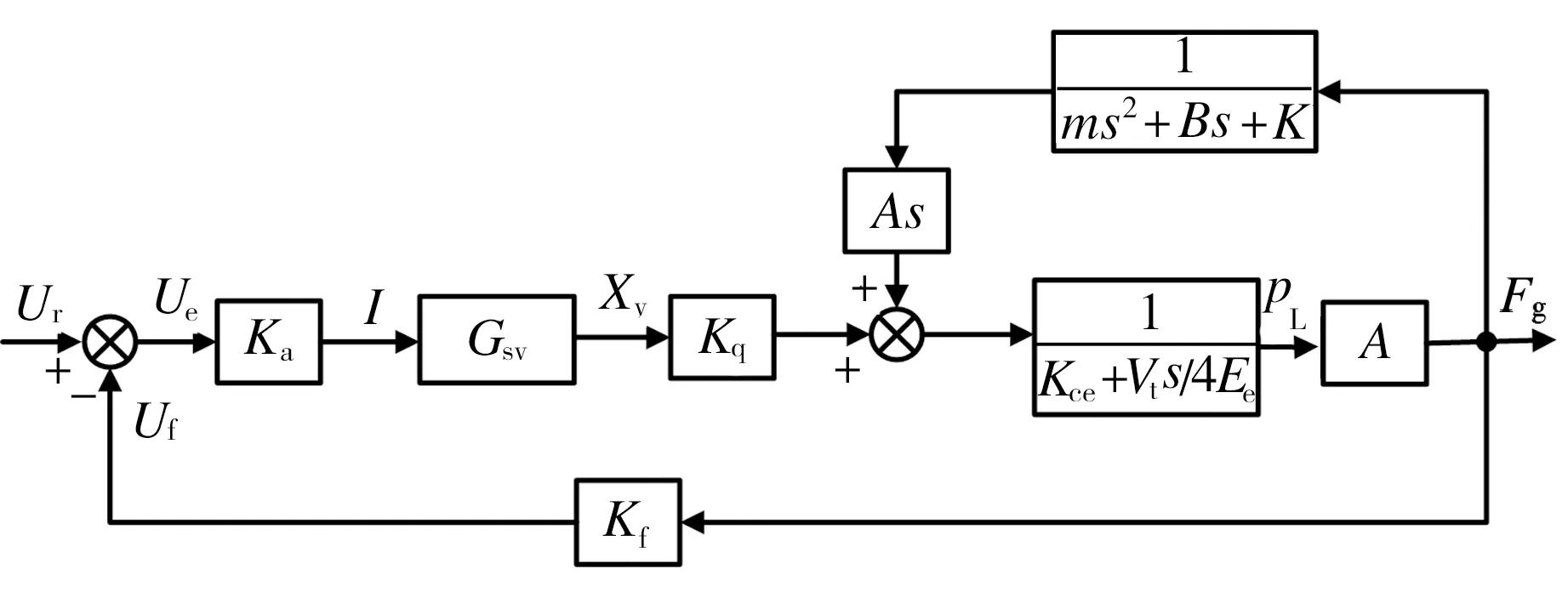
圖2 電液力控制系統簡化方框圖

Fig.2 Simplified block diagram of electro-hydraulic force control system

對圖2進行等效變化，可求得從閥芯位移Xv到液壓缸輸出力Fg的傳遞函數：

(1)

式中：m為活塞及負載折算到活塞上的總質量，kg；K為負載彈性剛度，N/m；A為液壓缸有效活塞面積，m2；B為運動部件黏性阻尼系數，N/(m/s)；Ee為油液有效體積彈性模量，Pa；Kq為閥口流量增益，(m3/s)/m；Vt為液壓缸總有效容積，m3；N1=BVt/(4EeA2)+mKce/A2，M1=mVt/(4EeA2)，Z1=KVt/(4EeA2)+BKce/A2+1，V1=KKce/A2，其中Kce為總流量-壓力系數，(m3·s)/Pa。

系統的閉環傳遞函數為：

(2)

式中:Ka為伺服閥放大器增益，A/V；Gsv為伺服閥的傳遞函數;Kf為力傳感器增益，V/N。

通過式(2)整理出電液力控制系統關于液壓缸輸出力的三階非線性方程：

(3)

式中：a=mVt/(4EeA2)；b=BVt/(4EeA2)+mKce/A2+mKaKfKqGsv/A；c=KVt/(4EeA2)+BKce/A2+BKaKfKqGsv/A+1；d=KKce/A2+KKaKfKqGsv/A；j=-UrKaKqGsv(ms2+Bs+K)/A。

將Fg記為f，則式(3)可抽象為：

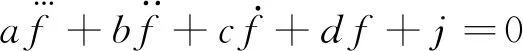
(4)

3 李雅普諾夫穩定性理論在電液力控制系統中的應用

3.1 電液力控制系統的狀態空間表示

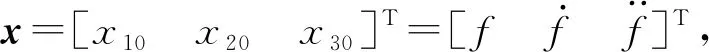
(5)

此狀態方程的平衡點為(-j/d，0，0)，通過坐標變換將平衡點移至坐標原點，令f=f-j/d，代入系統方程后得：

+(d1+d2)f=0

(6)

式中：a1=a，b1+b2+b3=b，c1+c2+c3+c4=c，d1+d2=d；b1=BVt/(4EeA2)，b2=mKce/A2，b3=mKaKfKqGsv/A，c1=KVt/(4EeA2)，c2=BKce/A2，c3=BKaKfKqGsv/A，c4=1，d1=KKce/A2，d2=KKaKfKqGsv/A。

由上述定義可知:a1代表慣性力變化引起的壓縮流量對輸出力的影響；b1代表黏性力變化引起的壓縮流量對輸出力的影響；b2代表慣性力變化引起的泄漏流量對輸出力的影響；b3代表系統質量的增益對輸出力的影響；c1代表彈性力引起的壓縮流量對輸出力的影響；c2代表黏性力變化引起的泄漏流量對輸出力的影響；c3代表系統阻尼的增益對輸出力的影響；c4代表液壓缸輸出力；d1代表彈性力引起的泄漏流量對輸出力的影響；d2代表系統剛度的增益對輸出力的影響。

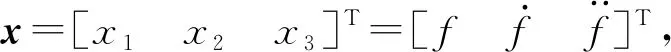
(7)

3.2 系統的鎮定

取式(6)的李雅普諾夫函數為：

V1(x)=(x1+x2)2+(x1+x3)2+(x2+x3)2

(8)

觀察式(8)可知，當x1=-x2、x3=-x1、x2=-x3，即x1=-x1、x2=x1、x3=-x1時，該函數在除了平衡點(0, 0, 0)之外的點都是大于零的，因此滿足正定條件。

式(8)展開后可得：

(9)

對式(9)求導，并結合式(7)可得：

=2[2x1x2+3x2x3+x1x3+

(10)

(11)

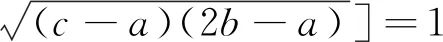
(12)

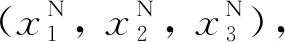
(13)

將式(13)代入式(10)，整理得到：

(14)

(15)

(16)

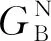
(17)

式中：e1=1；e2=3；e3=3；e4=1；e5=d2=KKaKfKqGsv/A。

本文選用文獻[11]中的系統參數，取系統負載剛度為60 kN/m，根據文獻[11]的參數值求出式(16)的各項系數值，如表1所示。

表1 式(16)的各項系數值

由表1可知，b2在二階系數項中起主導作用，c4在一階系數項中起主導作用，d1和d2在常值系數項中起主導作用。故式(16)可以簡化為如下形式：

(18)

由于式(7)是通過系統的閉環傳遞函數且將其平衡點變換至坐標原點后得到的，故這里將式(18)轉換為傳遞函數形式：

(19)

4 電液力控制系統結構補償方案的構造及穩定性分析

4.1 結構補償方案

假設進油路上的溢流閥起定壓作用，則進油壓力p10保持不變。在不考慮液壓泵的流量脈動、液壓缸內外泄漏、管道動態特性以及活塞和負載的黏性阻尼的情況下，系統動力學方程為：

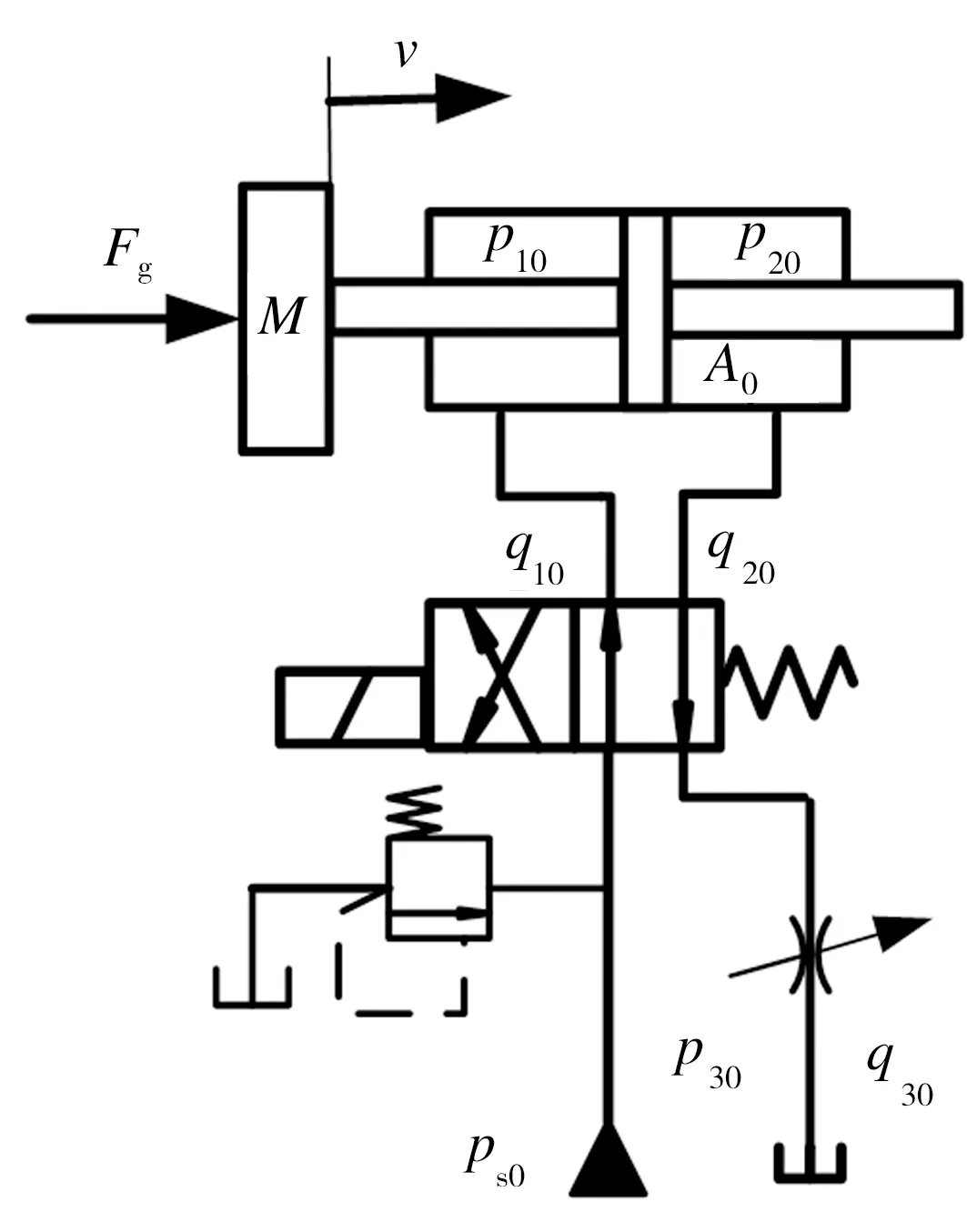
圖3 二階液壓補償器

(20)

式中：M為補償裝置質量，kg；Fg為補償裝置外負載力，N；v為活塞的運動速度，m/s；A0為液壓缸活塞的有效面積，m2；p20、p30分別為液壓缸出油腔壓力和節流閥出油口壓力，Pa。

通過節流閥小孔的流量為q0，略去二位二通換向閥泄漏和活塞徑向間隙中的泄漏，于是有

q0=A0v

(21)

取節流閥小孔的直徑為d、長度為l，液體流過小孔的平均流速為v0，則節流閥小孔層流沿程阻力損失的計算公式為：

(22)

式中：Re為雷諾數；ρ為液體密度，kg/m3。

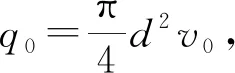
(23)

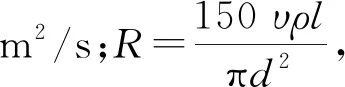
活塞運動時的阻尼力

(24)

將式(24)代入式(20)后，進行拉普拉斯變換，得到：

Fg-B0v=Mvs

(25)

液壓缸出油腔的液流連續方程為：

(26)

式中：V20為液壓缸出油腔的容積，m3；Ee為油液有效體積彈性模量，Pa；q20為液壓缸出油流量，m3/s。

節流閥閥口的流量方程為：

(27)

式中：C0為節流閥的節流口流量系數；w為節流閥的節流口面積，m2。

設系統供油壓力ps0由溢流閥調定為恒值，回油壓力p30為零，不考慮液流在管道中的損失及動態特性，油的溫度和密度均為常數，節流閥的負載壓力及流量特性為：

Δq20=Kq1Δw+Kc1Δp20

(28)

將式(26)線性化并將平衡工作點移至坐標原點，進行拉普拉斯變換可得：

(29)

當系統正常工作時，節流閥開度變化很小，故可認為Δw=0，于是式(28)可寫為：

Q20=Kc1P20

(30)

以P20A作為輸出量、力控制系統輸出力Fg作為輸入量，將式(25)、式(29)、式(30)整理得補償裝置系統傳遞函數為：

(31)

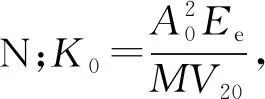
由于二階系統的重要參數是系統的無阻尼固有頻率和阻尼比，由式(19)可以知道，根據式(31)所構造的二階液壓補償器的無阻尼固有頻率及阻尼比與設計需求相匹配。二階液壓補償器與電液力控制系統的并聯結構如圖4所示。

4.2 二階液壓補償器的穩定性

據式(31)可知，構造的液壓補償器為二階系統，記式(31)的特征多項式為：

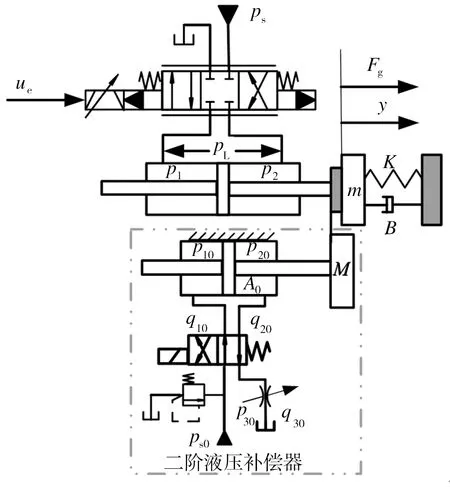
圖4 并聯結構補償方案

α2s2+α1s+α0=0

(32)

式中：α2=1,α1=(B0V20+MEeKc1)/(MV20),α0=B0EeKc1/(MV20)。

在式(32)中，阻尼系數B0、油液有效體積彈性模量Ee、液壓缸出油腔的容積V20及運動部分質量M皆大于零，同時，由于節流閥的節流口流量系數C0和節流口面積w、節流閥出口壓差p20-p30均大于0，故Kc1>0,所以系統特征方程的各系數均大于零。根據勞斯穩定性判據，二階系統穩定的充分必要條件為α2>0，α1>0，α0>0。由此可知，所構造的二階液壓補償結構是穩定的。

在液壓缸活塞運動過程中，缸內被壓縮的液體會產生與活塞位移成比例的復位力，此時被壓縮的液體可看作是一個線性液壓彈簧，其剛度則為液壓彈簧剛度[12]，該值是隨著活塞位移的變化而改變的。本系統液壓彈簧剛度的計算公式為：

(33)

式中：V1為進油腔容積，m3；V2為出油腔容積，m3。

(34)

根據式(32)、式(34)及圖2可以畫出加入二階液壓補償器后電液力控制系統的簡化方框圖，如圖5所示。

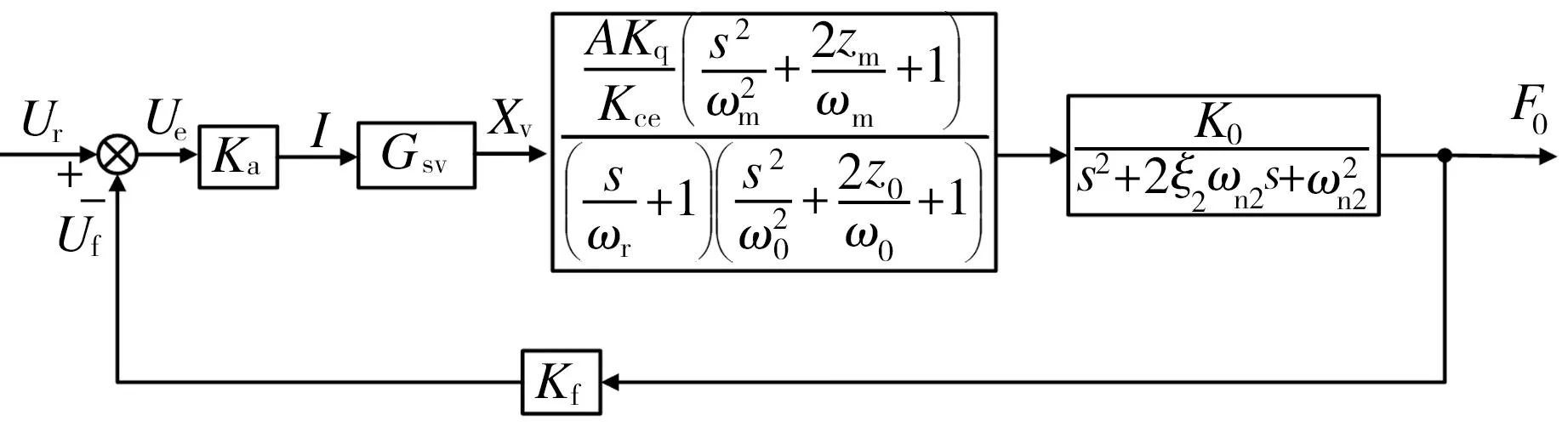
圖5 加入二階液壓補償器后的系統簡化方框圖

Fig.5 Simplified block diagram of the system with second-order hydraulic compensator

5 數值仿真分析

根據電液力控制系統的數學模型，建立Simulink數值仿真模型。設置步長為1×10-5s，采用ode45算法，計算相對誤差取1×10-6，按照表2中的參數進行仿真計算。

表2 液壓系統參數

從能量耗散的角度來分析，本文所構造的二階液壓補償器減小了系統綜合固有頻率ω0處諧振峰值的能量變化，提高了系統的綜合阻尼與液壓阻尼比，并且在動態過程中隨著彈性負載的變化而產生附加的阻尼作用，負載壓力變化越劇烈，其阻尼作用就越大，從而改善了系統的穩定性。而常規的雙慣性環節設計是在ωm之前串聯Gc=1/(s/ω1+1)2的校正環節，其中ω1為校正系數[12]。

圖6所示為電液力控制系統在未加入校正環節、加入二階液壓補償器和加入雙慣性環節后的系統伯德圖。在判斷系統穩定性時，一般情況下系統的相位裕度和幅值裕度越大，系統就越穩定。從圖6可以看出，系統加入二階液壓補償器后的幅值裕度為54.8 dB、相位裕度為108°，與加入雙慣性環節校正的系統相比(幅值裕度為18.2 dB，相位裕度為60.2°)，系統穩定性更強。另外，由于系統開環增益較小，故系統的穿越頻率僅有0.19 rad/s，從而使該系統的響應速度較慢。

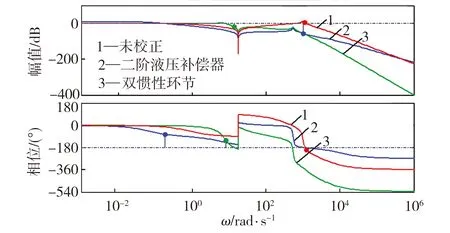
圖6 系統伯德圖

圖7所示為輸入指令力以2 kN為幅值作正弦規律變化時的系統輸出力與指令力的對比，其中，指令力F01=2sin(6πt) kN，F02=2sin(10πt) kN，F1、F2分別為F01、F02所對應的實際輸出力。圖8為在不同的方波信號指令力作用下，系統的實際輸出力與指令力的對比,其中，指令力F03、F04的周期T=0.5 s，幅值分別為8 kN和2 kN，F3、F4分別為F03、F04所對應的實際輸出力。

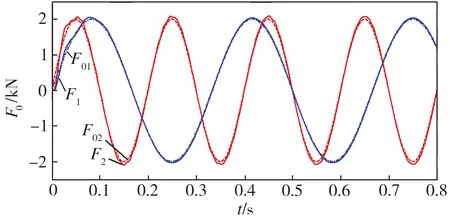
圖7 不同正弦信號指令力作用下系統的輸出力

Fig.7 Output forces of the system under different directive forces of sinusoidal signal

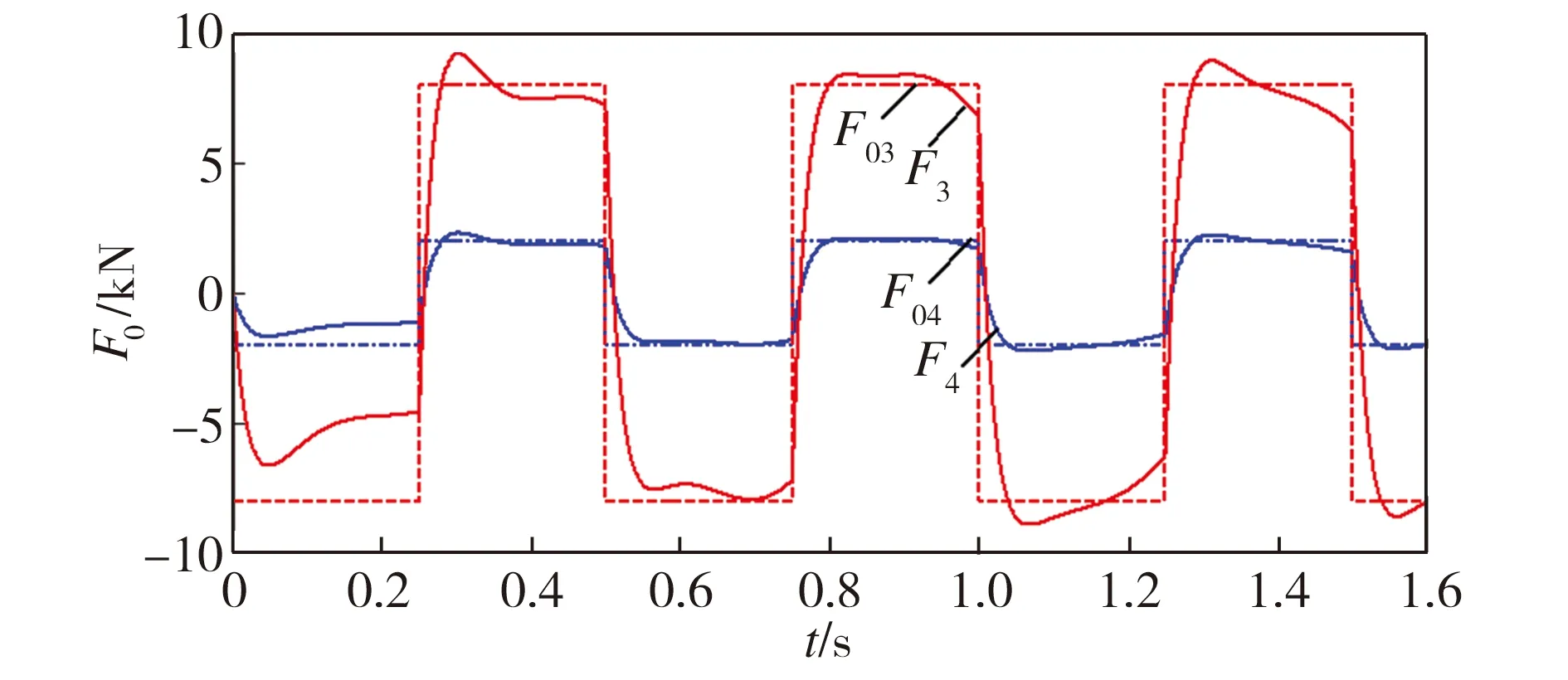
圖8 不同方波信號指令力作用下系統的輸出力

Fig.8 Output forces of the system under different directive forces of square signal

從圖7可以看出：正弦信號指令力頻率增大時，系統輸出響應變快，穩態誤差有所增大。當輸入正弦信號頻率為3 Hz時，系統能夠在0.12 s內達到穩態，輸出力的幅值誤差穩定在2.1%內，系統跟蹤性能良好；當輸入正弦信號頻率為5 Hz時，系統能夠在0.09 s內達到穩態，輸出力的幅值誤差穩定在3.7%內，跟蹤性能較好，但是存在發散的可能。從圖8可以看出：在相同頻率的方波信號指令力作用下，指令力增大會使系統響應品質降低。輸入方波信號幅值為8 kN時，系統達到穩態后的超調量最大為5.6%。從以上仿真結果可以得知，加入二階液壓補償器后的電液力控制系統的響應速度及跟蹤性能良好。

由式(33)可知，當活塞處在液壓缸兩端時，V1、V2取零，此時液壓彈簧剛度極大，液壓固有頻率的值也很大，系統有很好的穩定性，但精度很差。所研究的電液力控制系統的液壓彈簧剛度Kh與液壓缸活塞位移y的關系如圖9所示，可以看出，當活塞處在中間位置時Kh最小，當y=0或y=ymax=100 mm時Kh最大。

圖9 Kh與y的關系曲線

系統在二階液壓補償器的作用下，當液壓缸活塞在液壓缸右端運動、負載剛度K=60 kN/m時，可計算出活塞位移y為75、85、95 mm處的液壓剛度值Kh分別為73.1、105、249 MN/m。當輸入指令力為2 kN的階躍信號時，不同液壓剛度下系統的輸出力如圖10所示。

由圖10可以看出：當Kh不同時，系統的超調量和穩態誤差都發生改變；系統上升時間都在0.32 s以內，最慢在0.86 s內達到穩態，穩態誤差最大為0.09%。

當液壓缸活塞位于中間位置時，系統液壓剛度Kh=56.3 MN/m。仿真條件設置為：輸入指令力為2 kN的階躍信號，負載剛度K分別為60、300、600 kN/m。此條件下的系統輸出力如圖11所示。

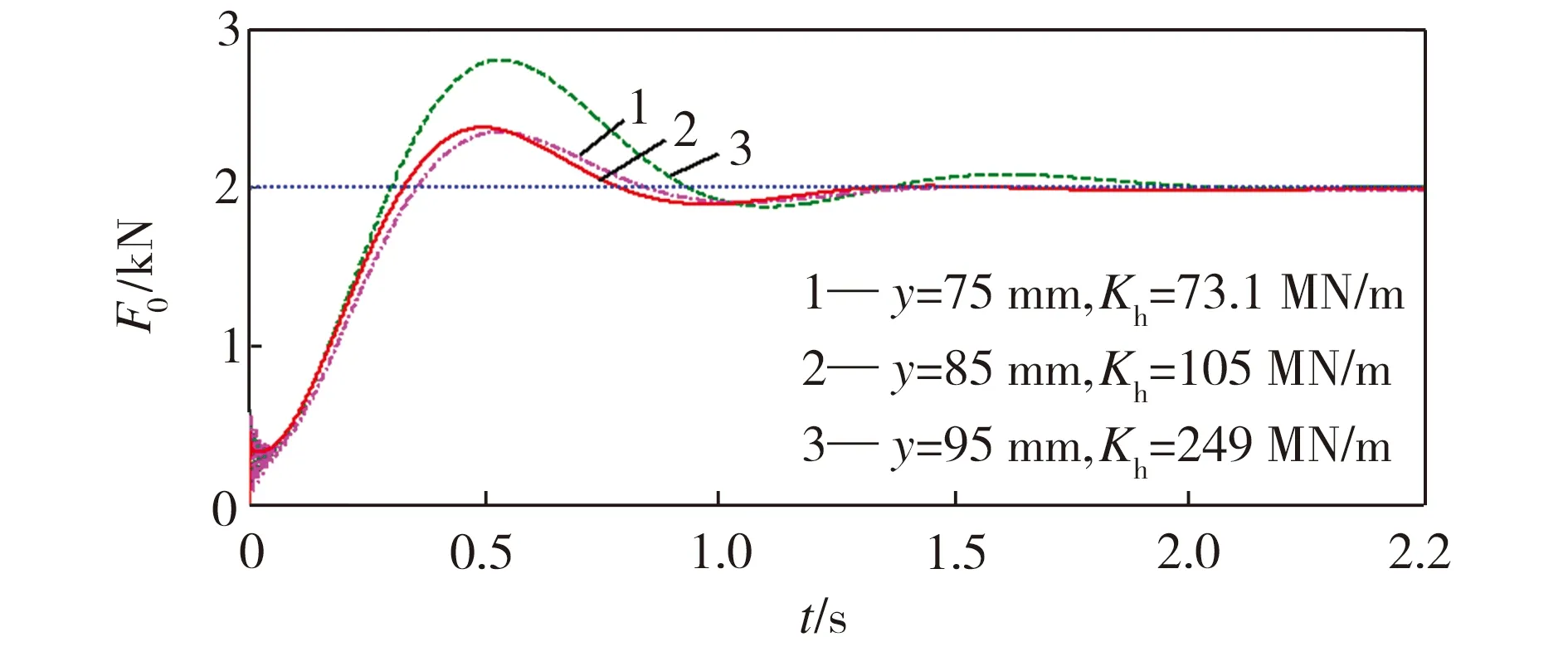
圖10 不同液壓剛度下系統的輸出力

Fig.10 Output forces of the system with different hydraulic stiffness values

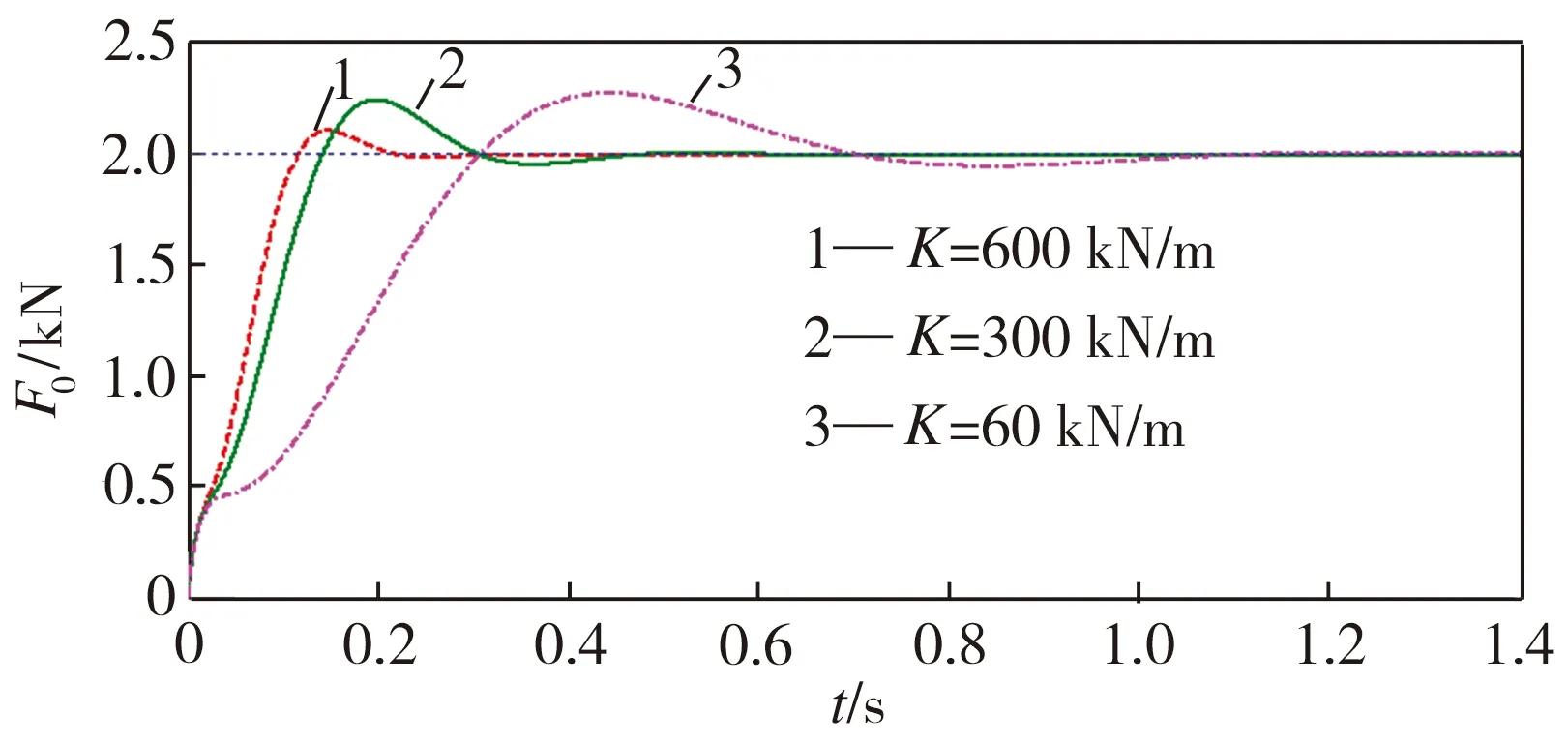
圖11 不同負載剛度下系統的輸出力

Fig.11 Output forces of the system with different load stiffness values

由圖11可以看出：當負載剛度遠小于液壓剛度時，隨著負載剛度的減小，系統響應速度變慢，穩態誤差增大，系統性能變差。當負載剛度為600 kN/m時，系統上升時間為0.09 s，輸出力能夠在0.24 s內達到穩態，輸出力幅值誤差穩定在0.4%內，系統跟蹤性能良好；當負載剛度為300 kN/m時，系統上升時間為0.15 s，輸出力能夠在0.41 s內達到穩態，輸出力幅值誤差也能夠穩定在0.4%內，但是超調量增加，系統響應變慢；當負載剛度為60 kN/m時，系統上升時間為0.65 s，輸出力在0.86 s內達到穩態，輸出力幅值誤差穩定在0.51%內。

下面對液壓缸活塞在接近于行程終端的位置、液壓剛度Kh=1440 MN/m、負載剛度K=60 kN/m的系統工況進行分析，此工況下系統的動態特性較差。當輸入指令力為2 kN的階躍信號時，分別加入二階液壓補償器和雙慣性環節以及未加入校正環節的電液力控制系統的輸出力如圖12所示，系統響應特性如表3所示。

分析表3可以發現，在輸入指令力為階躍信號時，系統在二階液壓補償器和雙慣性環節作用下均能夠準確地跟蹤期望的輸出力。但是與雙慣性環節的校正效果相比，系統在二階液壓補償器作用下的上升時間、峰值時間和調整時間分別縮短了68%、59%和37%，穩態誤差減小了0.1個百分點。

圖12 不同補償器作用下的系統輸出力

Fig.12 Output forces of the system with different compensators

表3 不同補償器作用下的系統響應特性

Table 3 Response characteristics of the system with different compensators

系統結構補償方案上升時間/s峰值時間/s最大超調量/%調整時間/s穩態誤差/%二階液壓補償器0.210.3513.40.860.51雙慣性環節0.650.8717.61.360.61未校正0.861.569.90.913.05

6 結論

(1) 根據電液力控制系統工作原理建立了系統的三階非線性微分方程，采用李雅普諾夫直接法對系統穩定性進行分析，得出滿足系統穩定性的條件，并根據數學模型及傳遞函數構造出二階液壓補償器的物理模型。

(2)二階液壓補償器能有效提高系統的穩定性并抑制諧振峰值。與雙慣性環節校正效果相比，系統在加入二階液壓補償器后的幅值裕度和相位裕度得到大幅度的提升，分別達到 54.8 dB和108°。

(3)加入二階液壓補償器后，對于不同頻率的正弦輸入信號，系統最慢在0.12 s內達到穩態，最大穩態誤差在3.7%以內。當系統輸入為頻率相同、幅值不同的方波信號時，系統達到穩態后的最大超調量為5.6%，輸入幅值增大時，系統響應品質會降低。

(4)負載剛度相同時，液壓彈簧剛度的改變導致系統超調量和穩態誤差均發生變化，但系統上升時間都在0.32 s以內，最慢在0.86 s內達到穩態，穩態誤差不大于0.09%。液壓彈簧剛度相同時，在負載剛度遠小于液壓彈簧剛度的范圍內，隨著負載剛度的減小，系統響應速度變慢，穩態誤差增大，系統品質變差。

(5)當液壓缸活塞接近于行程終端位置時，與雙慣性環節校正效果相比，系統在二階液壓補償器作用下的上升時間、峰值時間和調整時間大幅度縮短，穩態誤差減小，系統響應更快，動態性能更好。