基于磁場解析彈體飛行俯仰角的算法研究

于勇吉,林春生,翟國君

(1.海軍工程大學兵器工程學院,湖北武漢430033；2.海軍工程大學導航工程系,湖北武漢430031；3.海軍海洋測繪研究所,天津300061)

0 引言

隨著現代戰爭向信息化、智能化演變，常規彈藥命中率較低的特點使之不再適合于復雜的作戰環境使用[1]。目前彈體的飛行滾轉角方式主要有：基于陀螺儀的測量方法，利用無陀螺的慣性組合測量，利用太陽方位角傳感器進行測量，利用GPS導航器件測姿和運用地磁傳感器的測量方式。在上述測量方式中，陀螺測姿的漂移誤差會隨著時間而產生積累，解算精度無法保證[2-5]。利用慣性組合和GPS導航器件受制于安裝條件，太陽方位角傳感器受氣象條件影響較大。本文針對地磁傳感器解算俯仰角的算法進行研究。利用構建的彈體姿態數學模型，推導出飛行俯仰角的解算方程，并對地磁場解算俯仰角的算法進行仿真試驗和實物實驗驗證。

1 構建彈體姿態數學模型

建立彈體坐標系oxy和彈軸坐標系ox1y1z1[6-7]。模型中認為彈軸坐標系在初始發射時與彈體坐標系是重合的，彈軸坐標系的變化只與彈體俯仰和偏航的變化有關。模型主要研究彈體坐標系，其中ox軸為目標軸線方向，沿箭頭方向為正，oz軸垂直地面指向下，oy軸與ox，oz軸構成右手坐標系。大地磁場方向和大小用B表示，其在oxy面內的投影與ox軸的夾角定義為磁方位角H，由ox軸偏向oy軸正方向取正。磁傾角I為地磁場與oxy的夾角，向下偏為正。彈體坐標系如圖1所示。

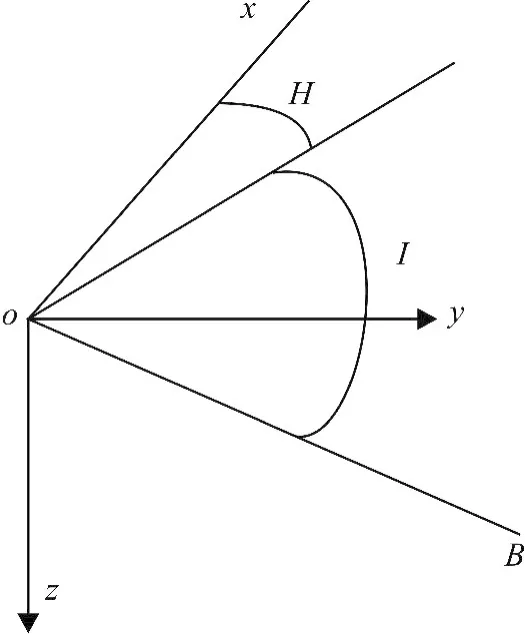
圖1 彈體坐標系示意圖Fig.1 Schematic diagram of projectile’s coordinate system

彈體在短距離飛行過程中地磁場矢量基本保持不變，可將其視為常量。由圖1可得地磁場在彈體坐標系oxyz上各軸的投影分量為[8]

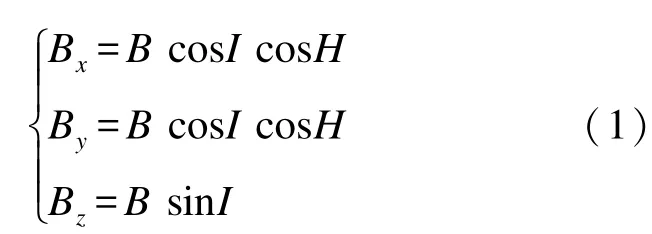
當不考慮滾動時，假設彈體以一定的俯仰角P直線飛行時，地磁場在彈體坐標oxyz上各軸的投影分量可以表示為

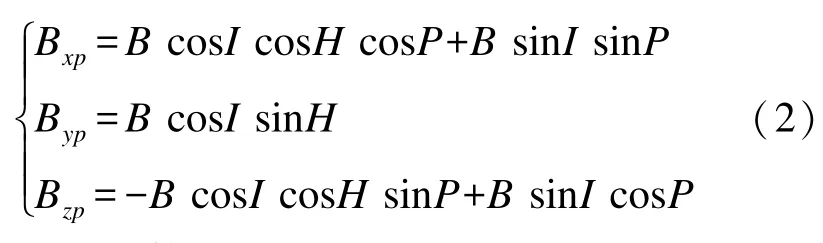
若考慮彈體做小范圍搖擺和俯仰隨機運動，只需考慮俯仰角和磁航向角的時間變化，則有磁方位角和俯仰角的變化公式為[9]

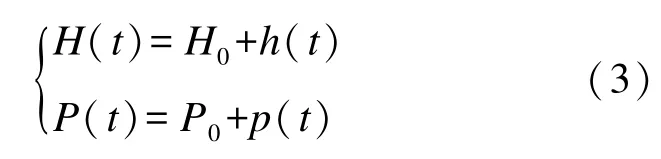
2 利用加速度計解算彈體俯仰角

通過加速度計測量彈體飛行俯仰角時，忽略加速度計離心力的影響，即將加速度計視為安裝在彈體的旋轉中心附近的理想狀態，另外不考慮彈體章動角對于加速度計幅值的影響，其中g為重力加速度。彈體所受重力加速度在彈體端面上的投影如圖2所示。

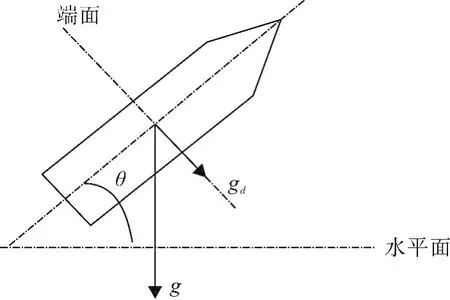
圖2 重力加速度在彈體端面上的投影圖Fig.2 Projection of gravity acceleration on end face of projectile

彈體在整個飛行過程中忽略風的阻力，且旋轉過程視為勻速轉動，不考慮彈體的切向加速度，那么加速度計的理論測量值為重力加速度與離心加速度[10]，由圖中幾何關系可得重力加速度g在彈體端面上的投影分量gd為

圖3為彈體截面圖，可求得g在彈體截面上的投影分量gd分別沿彈體徑向和軸向上的分量為因此加速度計兩軸的輸出值為

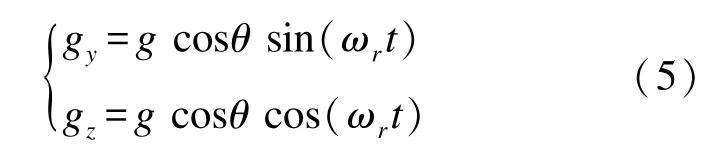
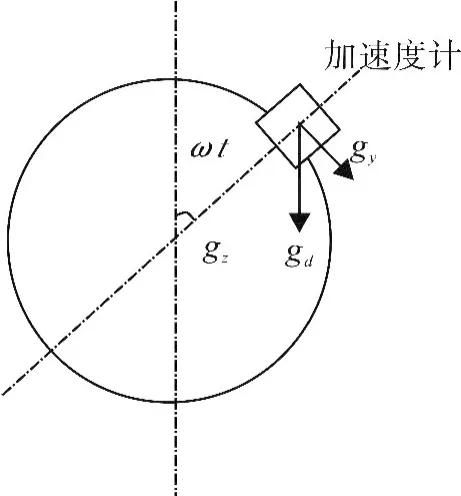
圖3 彈體截面圖Fig.3 Sectional view of projectile

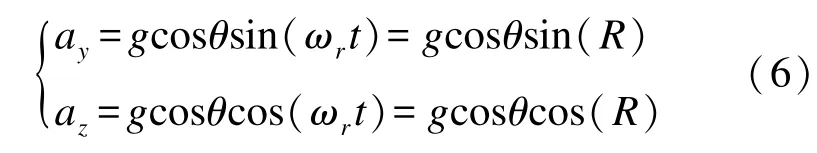
因此采用加速度計解算出的俯仰角和滾轉角為

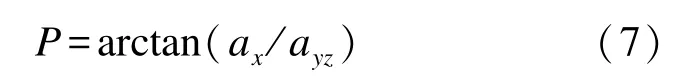
但在實際測量中，由于加速度計受到離心加速度的影響，加速度計三軸的測量值會存在較大偏差，由此本文選用利用地磁進行彈體俯仰角的解析。

3 地磁傳感器求解彈體俯仰角

對地理坐彈體相對地磁俯仰角Pc(t)做出分析。俯仰角Pc(t)為地磁場在xBOzB面內的投影與彈體OxB軸的夾角，規定向下為正。當彈體平行飛行時，俯仰角P=0，初始相對地磁俯仰角為[10]

由地磁投影關系可知，地磁場在補償彈體滾轉角之后，在OzB軸上的投影為Bz0(t)，則地磁場在坐標面xBOzB的投影為

則相對地磁俯仰角瞬態值為

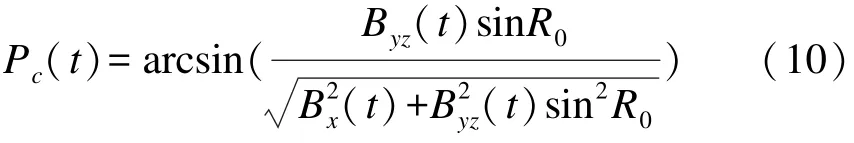
由式(8)和式(10)，得到彈體瞬時俯仰角P(t)為

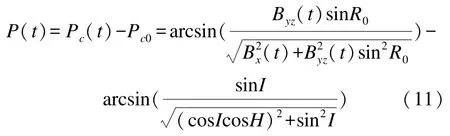
在短時間內平均俯仰角可近似計算為

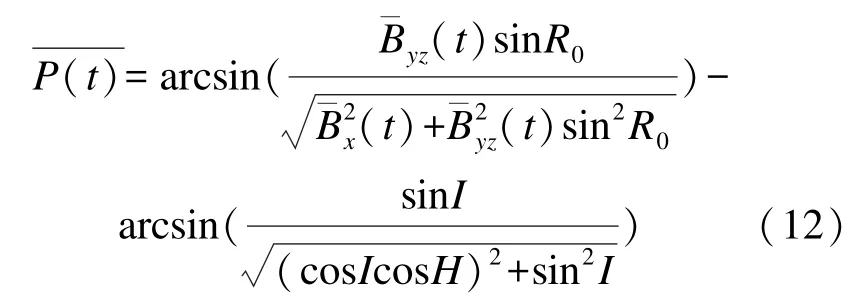
根據式(12)，在已知I和H的條件下，可以得到短時平均俯仰角

4 俯仰角測量試驗

根據磁場解算俯仰角的方法分別進行算法仿真試驗和單片機控制的地磁傳感的實物實驗。

4.1 算法仿真實驗

為了驗證算法的可行性，本文進行算法仿真。首先進行彈道仿真，給定初始條件：地磁場50 000 nT，磁傾角I=45°，方向斜向下，初始磁航向角H0=15°，彈體滾轉角速率為200 r/s，俯仰姿角姿態維持在-10°(下壓為正)，全程不考慮偏航角的變化，算法采樣率為720 Hz，采樣點為40 000個。為模擬真實的彈道參數，將仿真出來的磁場測量值添加上均值為0，方差為0.1 uT的高斯白噪聲。得到的俯仰角度及其誤差如圖4-5所示。

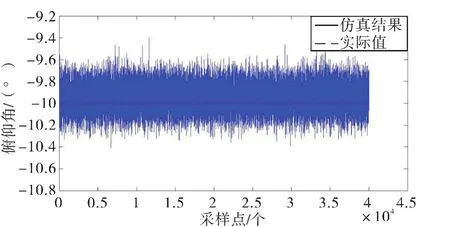
圖4 俯仰角度示圖(200 r/s)Fig.4 Schematic diagram of pitch angle(200 r/s)

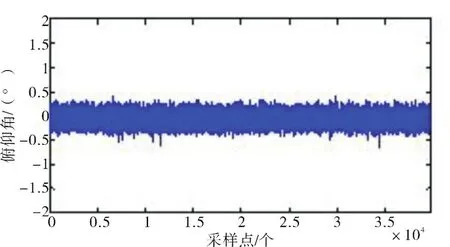
圖5 俯仰角誤差示圖(200 r/s)Fig.5 Schematic diagram of pitch angle’s errors(200 r/s)

保持平飛狀態，地磁場噪聲信號均值為0，方差為0.1 uT，改變轉速由200 r/s變為100 r/s，進行比對仿真試驗，得到仿真結果如圖6-7所示。

綜上，俯仰角的解算誤差在±0.4°以內，誤差沒有出現發散。

現對俯仰角發生變化的情況進行仿真分析。設定仿真所需要的初始條件不變，彈體自身旋轉速度為200 r/s，設定俯仰角從-10°變化到30°。 得到圖8-9所示結果。

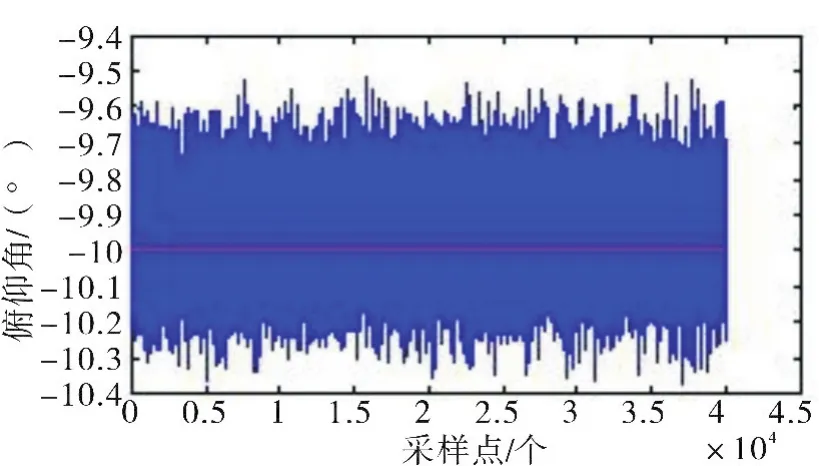
圖6 俯仰角度示圖(100 r/s)Fig.6 Schematic diagram of pitch angle(100 r/s)

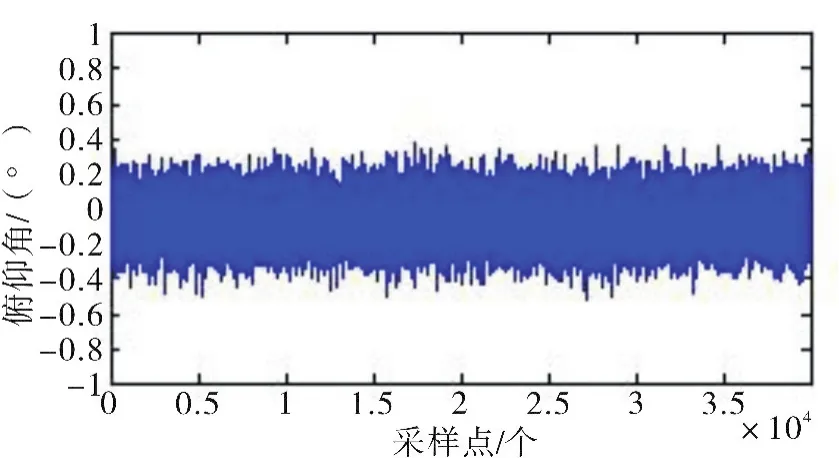
圖7 俯仰角誤差示圖(100 r/s)Fig.7 Schematic diagram of pitch angle errors(100 r/s)

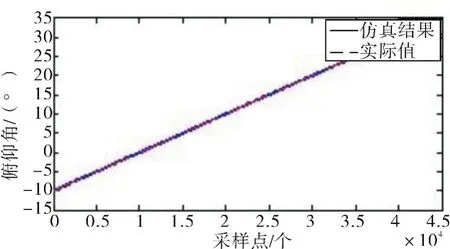
圖8 俯仰角度示圖Fig.8 Schematic diagram of pitch angle

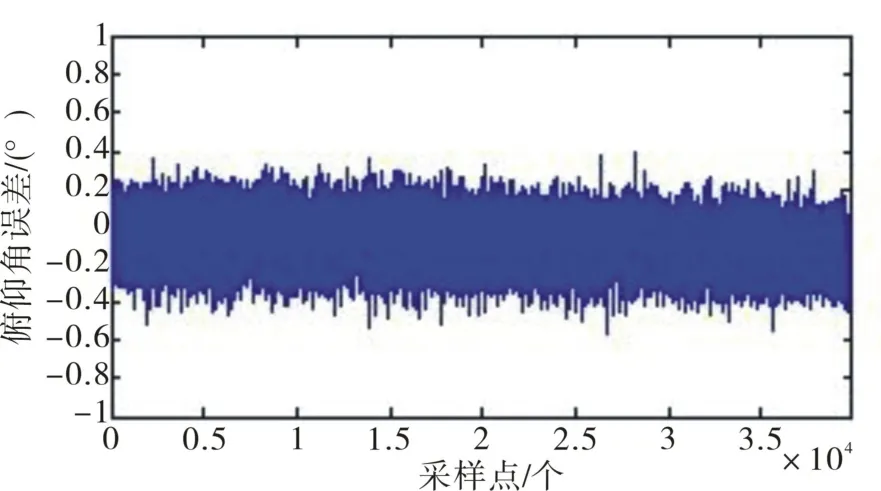
圖9 俯仰角誤差示圖Fig.9 Schematic diagram of pitch angle’s errors

從仿真實驗結果可知：運用本算法解算出的俯仰角不隨采樣點的增多而產生誤差積累。如圖4-9所示，姿態角變化與理想值比對具有相同的變化規律。由此驗證了算法的可行性。

4.2 地磁傳感器解算滾轉角實驗

本實驗選用的傳感器是HoneyWell公司的HMC5883L型號磁傳感器。選用的核心控制單元為STC15型單片機。測量系統組成的原理框圖如圖10所示。

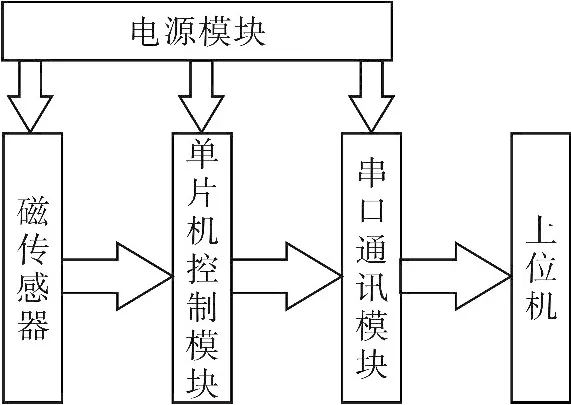
圖10 系統硬件組成示意圖Fig.10 Constitutional diagram of system hardware

在三軸實驗轉臺上進行實驗，設定轉臺內軸勻速旋轉，角速度為0.872 5 rad/s，外框方位角保持為0°，進行彈體飛行俯仰角的模擬實驗。設定轉臺中軸俯仰狀態為正向5°(俯仰向下為正)，得到如圖11和圖12所示俯仰角及誤差示圖。

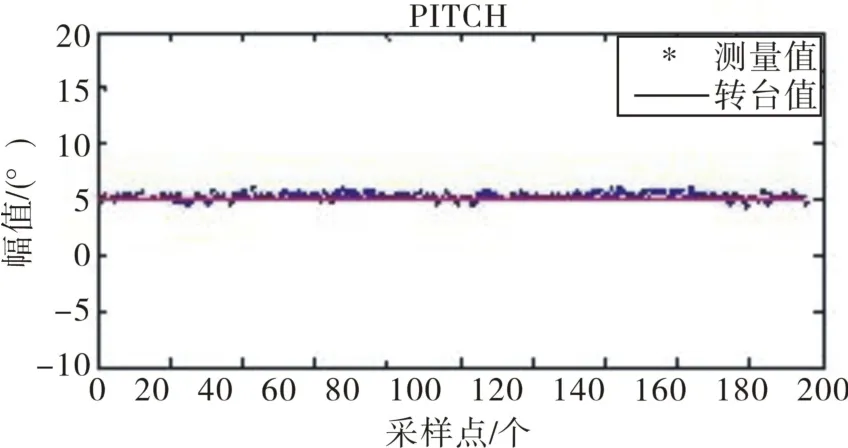
圖11 俯仰角度示圖Fig.11 Schematic diagram of pitch angle

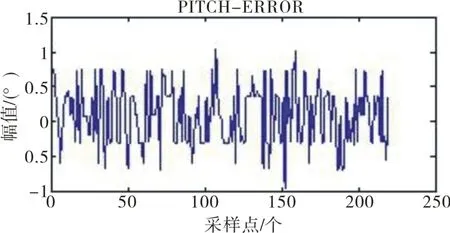
圖12 俯仰角度誤差示圖Fig.12 Schematic diagram of pitch angle’s errors

由圖11和圖12可以看出，改變俯仰狀態為負向后俯仰角誤差仍然在±2°以內，屬于合理的誤差范圍。

最后分析得出，實驗結果與仿真結果相吻合，進一步驗證了算法的正確性、合理性。同時隨著俯仰狀態改變，解算出來的俯仰角誤差仍在合理范圍內，表明其具有優越性與工程價值。

5 結束語

本文在建立的彈體姿態數學模型上，進行了地磁傳感器解算俯仰角的算法研究。發現根據地磁解算彈體俯仰角，誤差不會隨著彈體轉動而產生累積。最后，分別進行算法仿真和實物測量，結果表明該算法在彈體飛行俯仰角解算上的可行性，同時算法簡單有效，在工程應用方面有廣闊前景，與其他彈體俯仰角測量方法相比具有更高的實用價值。