一種發射平臺水面多彈分離過程的運動特性分析

張 春,王宇翔

(中國船舶科學研究中心水動力學國防科技重點實驗室,江蘇無錫214082)

0 引言

水下運載器可攜帶導彈、無人機等多種任務載荷，在未來戰場上具有重要的軍事價值和廣闊的應用前景[1]。近年來，美國提出了“深海浮沉有效載荷(UFP)”研究計劃，該計劃旨在研發一種長時間潛伏的分布式無人跨介質作戰系統[2]。對于該類武器系統，水下運載器攜帶載荷至水面并快速完成分離是不可或缺的一個重要環節。

水面分離方案是指運載器以一定速度和姿態角運動至水面，在水面導彈與運載器進行熱分離或冷分離[3]。分離后的導彈飛向攻擊目標，運載器沉入水中。一般的，武器水面分離采用干式發射技術，美國“魚叉”飛航導彈和法國“飛魚”飛航導彈均采用該技術實施水下發射[4]。在彈器水面分離過程中，系統內力主要包括2個部分，即適配器的約束力和彈器的分離力。其中，分離力一般有2種方式實現：一種是利用載彈自身發動機推力，即自推力分離方式；另一種則是由發射平臺內部的燃氣發生器提供分離所需能量。常規彈器水面分離過程主要針對單一導彈的水面分離[5-8]，而對于一次性可攜帶多枚導彈的水下運載器而言，其多枚導彈水面彈器分離的過程更為復雜，針對該過程的建模和仿真并不多見。

本文以發射平臺水面逐一發射多枚導彈的技術方案為背景，利用多剛體運動模型對動基平臺的水面多彈分離過程進行了數學建模，并分析了三維模型中力矩陣內的各個參數。為滿足方案設計初期的工程估算需求，將三維模型進一步簡化為一維模型，編寫了可實現任意裝填枚數的動基平臺水面多彈分離過程動力學仿真軟件，分析了平臺出水速度、導彈裝填枚數以及導彈發射間隔等參數對分離過程的影響規律。

1 水面多彈分離過程的物理描述

水下運載器上浮至近水面時開始快速拋離浮力殼體、密封頭蓋等部件，并由此進入任務載荷水面分離過程。假設以導彈為任務目標，此時運載器可簡化為一個裝有多枚導彈的水面動基發射平臺(以下簡稱為發射平臺)，其示意圖如圖1所示。

圖1 發射平臺水面多彈分離過程示意圖Fig.1 Schematic diagram of multi-projectile separation process on water-surface from launching platform

導彈與發射平臺之間通過若干道適配器相互約束，分離過程中剛體間的相互關聯則體現在對適配器約束內力、內力矩的確定上。在各枚導彈的發射過程中，發射平臺可看作為一個變質量的動基發射平臺。根據單枚導彈與發射平臺的相對位置，可將導彈的動力學過程分為3種狀態：第一種是導彈處于待發射狀態，此時導彈與發射平臺保持相對靜止，導彈和發射平臺因而組成運動聯合體，其運動狀態由聯合體的運動狀態確定；第二種是導彈正處于分離狀態，此時導彈的運動參數由自身的動力學模型所確定；第三種是導彈已完全從發射平臺中分離，其在空氣中的運動特性可不予考慮。

2 水面多彈分離過程數學建模

2.1 水面多彈分離過程三維動力學模型

在描述導彈、發射平臺的運動和各項受力之前，分別建立大地坐標系O0xyz、發射平臺坐標系O1x1y1z1以及導彈坐標系O2x2y2z2。發射平臺外形分別關于x1O1y1和x1O1z1面對稱，各表征運動、力的物理量在隨體坐標系與大地坐標系的聯系可通過坐標轉換矩陣得到。

將發射平臺的隨體坐標系看作為運動聯合體的動坐標系，即運動聯合體動坐標系原點取在發射平臺質心。根據動量與動量矩定律，可以得到運動聯合體在導彈水面分離過程中的動力學方程組：

式中Amλ為慣性矩陣，即

AVω為速度矩陣，即

AFM為力矩陣，通常包含定常水動力、浮力、重力、推力及相應的力矩等。

水面動基發射平臺多彈分離過程本身是一個三維過程，平臺在內外力的共同作用下做非定常運動。其中，內力主要包括適配力和分離力等，外力則包括浮力、附加質量力以及定常水動力等。因此，合理、可靠的三維動力學模型能準確地描述各剛體的運動及相互之間的作用。但是，從給出的三維動力學模型中可以看出，該模型的求解主要依賴于各剛體慣性矩陣和力矩陣的確定。即：一方面要獲得分離過程中運動聯合體的質心坐標、慣性張量；另一方面必須基于很多假設獲得力矩陣的表達。其中，特別難以確定的是，三維空間下的導彈適配力、分離力與相應力矩，而這些力及力矩對系統的轉動參數有重要影響。因此，關于水面動基發射平臺多彈分離過程的三維動力學模型求解需要進一步開展相應的實驗研究。

2.2 水面多彈分離過程一維簡化模型

發射平臺由于可容納多枚導彈，相較于單枚導彈而言，其質量和轉動慣量大很多。當發射平臺垂直浮出水面開始分離時，在分離方案設計階段，可暫時忽略分離系統內力對其轉動過程，將水面多彈分離過程簡化為一維情況。即，在整個分離過程中忽略轉動，只考慮軸向運動；一維模型不考慮系統轉動，只考慮單向自由度。

假設發射平臺共搭載n枚質量均為mm的導彈，其中第i枚導彈處于發射狀態，則發射平臺的運動方程為

該導彈的運動方程為

1)浮力 Fb。

當頭部出水并距離水面為xte，則發射平臺受到的浮力為

2)定常水動力Fh。

由于發射平臺只有軸向運動，可以利用平板的摩擦阻力公式近似考慮流體粘性影響，即

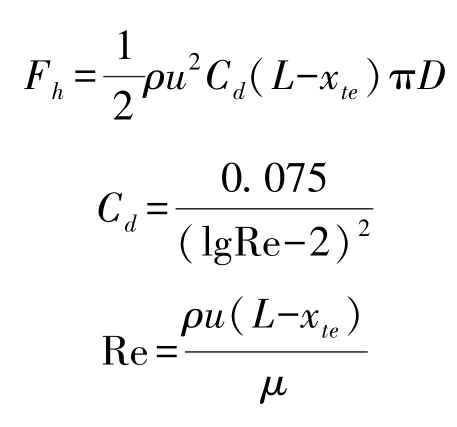
3)附加質量力 mhλ。

發射平臺的附加質量可近似看出一個常數，為

4)適配器摩擦力Fc。

適配器共4道，并隨著導彈出筒，其相對運動逐漸減少，其有效適配器個數根據相對位置確定。當適配器未脫掉時，單個適配器的摩擦阻力由預緊力產生，如下：

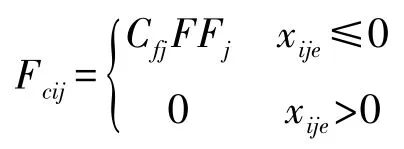
5)分離力FSC。

當采用自推力方案分離時，發射平臺受到的后座力較小，分離力近似為0，即

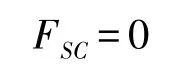
當采用燃氣彈射作用力時，發射平臺受到的后座力較大，近似計算時看作為一個常數：

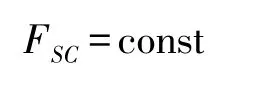
3 結果分析與討論

3.1 出水速度對水面分離過程的影響

為滿足方案設計初期的工程估算需求，將三維模型進一步簡化為一維模型，編寫了可實現任意裝填枚數的動基平臺水面多彈分離過程動力學仿真軟件。

圖2 不同出水速度時的運動參數變化曲線Fig.2 Changing curve ofmotion parameters at different water-exit speeds

圖2為發射平臺不同出水速度時的運動參數變化曲線，仿真參數為總體方案的設計值。可以看出，發射平臺出水速度越高，各運動物體的位移變化越明顯，導彈的離筒速度也更高。同時，由于導彈分離力相對于發射平臺質量較小的原因，各枚導彈的分離時間也較為接近。當發射平臺低速出水時，發射平臺可近似為水面浮筒，發射過程容易受風浪因素影響，方案設計時要重點考慮耐波性問題。當發射平臺高速出水時，完全出水后做自由落體運動，其有效發射窗口時間相對于水面浮筒來說較小，直接限制了發射平臺的可裝填導彈枚數。

3.2 發射間隔對水面分離過程的影響

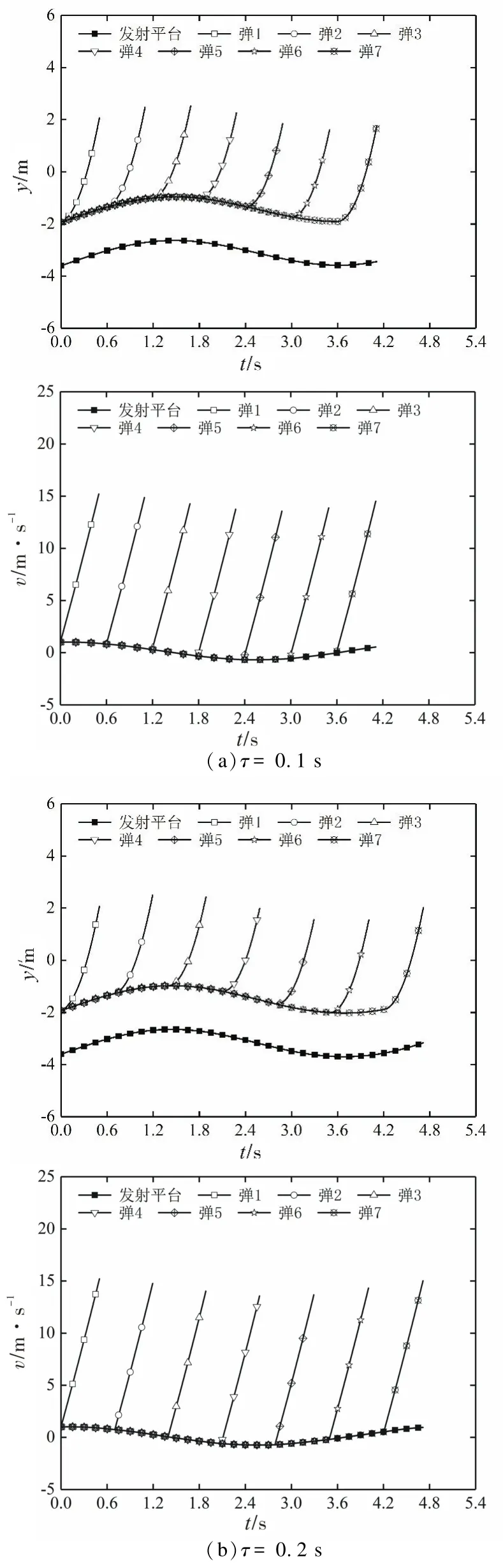
圖3 不同導彈發射間隔的運動參數變化曲線Fig.3 Changing curve ofmotion parameters at different launch intervals

圖3為發射平臺(7枚裝彈)在不同發射間隔時的運動參數變化曲線。可以看出，在前3枚導彈發射過程中，平臺處于上升過程，前2枚導彈的離筒速度均在15m/s左右。第4、5枚導彈發射時，平臺質心下降，存在一個負向的速度，導彈的出筒速度也較低。第6、7枚導彈發射時，由于平臺仍然有向上的運動速度，導彈離筒速度與第1、2枚導彈比較相似。對于可近似看作為浮筒發射的水面分離過程，發射間隔減少后，各枚導彈在筒內運動時間和出筒速度變化不明顯，但整個水面分離過程持續的時間會大幅度減少，這會增加平臺武器發射的快速性。當發射平臺高速出水后，由于分離過程的發射窗口時間持續較短，各枚導彈的發射間隔越小，發射系統的快速性越好。因此，對于水面多彈分離過程，在保證發射平臺動穩定的基礎上，發射間隔越短越好。

3.3 不同分離力實現方式的影響

分離力是完成導彈水面分離過程的動力，不同分離力的實現方式會影響到發射平臺的運動過程，例如當發射過程采用彈射類的方式時，則需要考慮后坐力對平臺運動的影響。

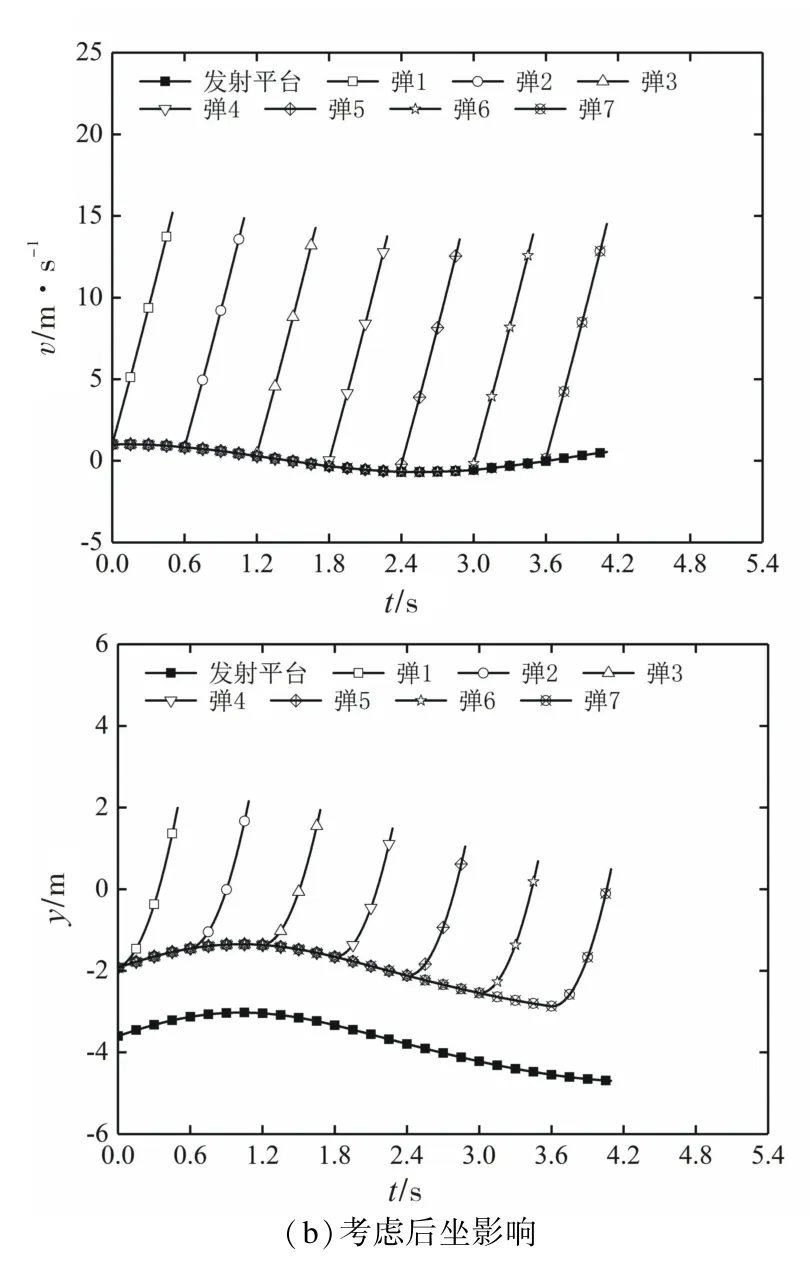
圖4 不同分離力實現方式時的運動參數變化曲線Fig.4 Changing curve ofmotion parameters at different implementation ways of separation forces

圖4為不同分離力實現方式時的運動參數變化曲線。從曲線來看，在前3枚導彈發射過程中，發射平臺和導彈運動參數較為接近，表明分離力對平臺影響較小。當平臺繼續發射導彈時，發射平臺質量逐漸減少，質心會逐漸下降，后座力產生的不利影響也不斷增加。此外，對于有后座力的水面多彈分離過程，發射平臺可能會被再次推入水中，影響發射平臺的有效發射窗口時間。因此，為保證發射平臺的導彈裝填量，應盡量減小各枚導彈發射過程所引起的后座影響。

4 結束語

本文以發射平臺水面逐一發射多枚導彈的技術方案為背景，利用多剛體運動模型對動基平臺的水面多彈分離過程進行了數學建模，分析了平臺出水速度、導彈裝填枚數以及導彈發射間隔等參數對分離過程的影響規律。得到了以下幾個結論：

1)當發射平臺以導彈裝填量為設計目標時，平臺應低速出水，此時要重點考慮發射過程中的耐波性問題；當發射平臺以發射快速性為設計目標，平臺則需要高速出水，發射平臺重力應小于浮力。

2)當發射平臺低速出水并可近似為水面浮筒時，平臺在導彈分離過程中會在水面做低幅度的上下振蕩，發射過程中盡量保證平臺浮心高于質心，以提高各枚導彈發射過程中的穩定性。

3)當發射平臺低速出水并考慮發射后坐影響時，由于后坐力的存在，發射平臺可能會被再次推入水中。因此，發射平臺方案設計時應充分考慮后坐力帶來的不利影響。

限于運載器發射平臺水面分離多枚導彈還處于方案考慮階段，本文將三維模型簡化為一維模型。以后的工作中，需要結合發射過程中的具體方案及其關鍵參數，逐步完善計算方法，進一步認識水面多彈分離過程的動力學問題。