不等式部分的易錯題型與解題技巧
程雅雯
(江蘇省宜興第一中學 214206)
一、不等式恒成立問題及其解題技巧
針對該種類型的數學問題,適宜采用分離變量或適當變形,或者采用主元變換法,又或者先進行構造函數,之后運用函數的單調性等性質來進行求解.如果涉及到最值問題,那么在求解中可以采取基本不等式來進行求解.
例1已知不等式2ex-nx+15>0在實數集R上恒成立,試求正整數n的最大值.
解析針對該道不等式恒成立問題,求解過程中可以直接采用構造函數f(x)的方法,令f(x)的最小值大于0,那么就可以解決該問題,又或者可以將該不等式進行適當變形,轉化成兩個形式比較簡單的函數,之后基于這兩個簡單函數的圖象性質,利用數形結合法來求解問題.
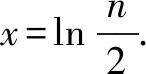
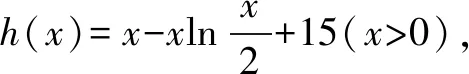

解法二(不等式變形+數形結合法):根據題干信息,可以將原不等式轉化下式:2ex+15>nx.
當x≤0時,原不等式恒成立.

假定h(x)=(2x0-2)ex0-15(x>0),那么可知h′(x)=2xex>0,所以函數h(x)在x>0上為單調增函數.又因為h(2)<0,h(3)>0,所以可知必然存在x0∈(2,3)使得h(x0)=0.由此可知,k=2ex0∈(2e2,2e3),且2ex0>2e2>14.由此可知,nmax=14.
二、高次不等式問題及其解題技巧
高次不等式也是高考數學學科常考的一個知識點.我們高中生求解這類數學問題的時候往往會因為搞混區域而出錯,且在判斷特殊點或區域的時候存在不明確的問題,尤其是我們當中許多學生可能會在看到高次不等式這種復雜題型的時候就心生畏懼,不知道該如何下筆進行求解.針對該類數學題型,我們要正確認識并要學會熟練運用“穿根法”這種解題方法,這會提升我們解題的準確度與效率.在求解解集后,還要注意仔細地判定解集的臨界點,看是否將其納入到解集范疇.
例2已知不等式(x+3)(x-2)(x-4)≤0,試求其解集.
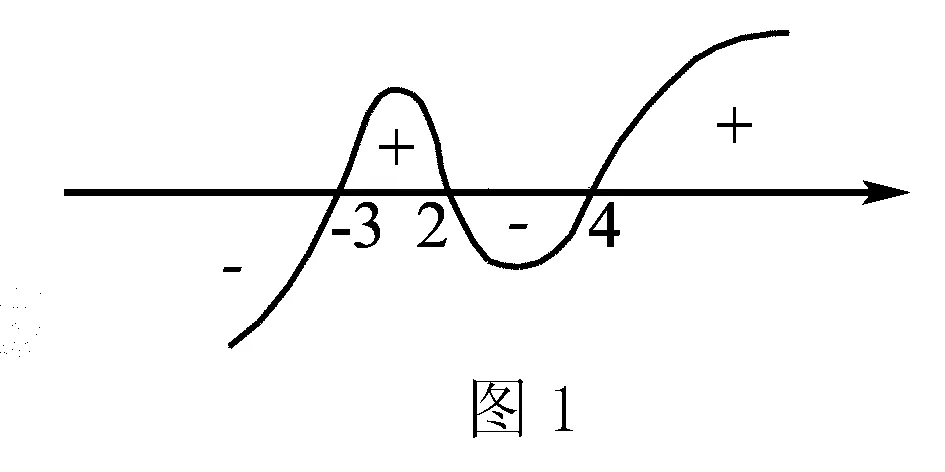
解析該道高次不等式問題是一種常見的問題,不需要進行因式分解即可判斷相應函數的三個根,即-3,2和4.然后我們可以按照”穿根法“的基本應用方法.在數軸上面分別標出x=4,x=2和x=-3三個零點的坐標,這樣就可以將數軸劃分成4個區間,然后從最右側(x=4)開始,從右上方經過零點后向左下方穿過,之后依次穿過x=2和x=-3這兩個零點,這樣就構成了圖1所示的一條函數曲線圖.然后根據題干要求,只需要選擇滿足圖象位于數軸之下圖象即可,但是需要注意的是,該道不等式問題中給出的是“≤”,所以求解過程中需要將相應的邊界值納入到解集當中,即最終這道題的正確答案為:(-,-3]∪[2,4].
三、結合線性規劃的不等式問題及其解題技巧
對于這類數學問題,一般都是求解目標的最值問題,但是卻涉及到定義域和面積求解等相關數學知識,實際求解中需要充分了解不等式和線性規劃等方面的相關數學知識,明確這些知識之間的聯系性,這樣最終才能準確地求解相關數學問題.歸納起來,在求解該類不等式問題的時候,如果遇到求解極值的問題,那么需要先繪制出不等式組的可行域,將其轉化成幾何知識后,再將不等式相應地轉化成等式問題來進行求解.又或者可以將不等式轉化為函數,并為其設定一部分參考值,基于函數視角來觀察不同參考值變化下函數圖象對應的變化情況,最終明確影響函數變化的相關量,并求解該問題.
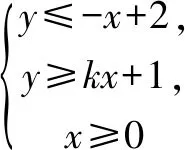
A.-1 B.-1/2 C.1/2 D.1
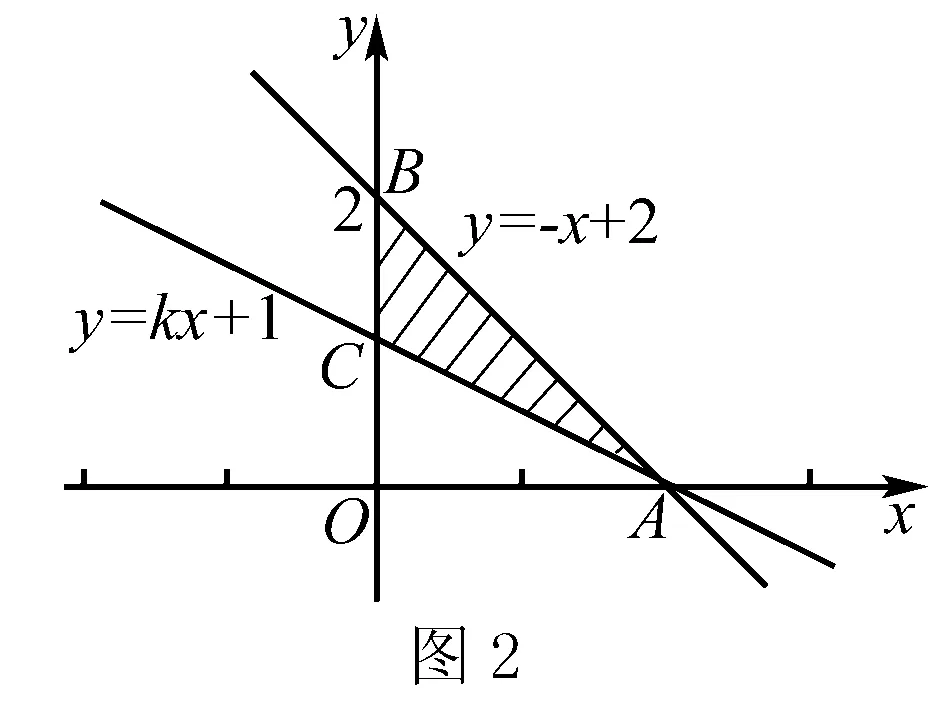
解析該道不等式問題的難點和易錯點在于確定三條給定直線所構成的區域以及區域面積的計算.針對該道問題,可以先根據不等式組來繪制出三條直線,繪制出圖2所示它們圍成三角形的示意圖,之后可以將上述給定的4個選項分別代入后即可直觀地確定這道題的正確答案為B.
總之,科學、合理的解題技巧往往會使解題事倍功半,是提升我們求解不等式問題等數學問題準確率和效率的有效手段.因此,我們高中生在平時的學習中要注意多歸納和總結一些常用的解題方法,并要強化專項解題技巧的訓練,確保不斷提升自身的數學問題求解能力.

