距離和容量雙重限制下多配送中心選址模型的應用

高原

[摘要]本文首先分析在選址過程中進行帶距離限制和帶容量限制原因，先利用連續性選址重心法及帶距離限制的選址模型求得初始解，解決配送中心間調撥運輸過高問題，然后運用距離限制模型對初始解進行優化，防止配送中心建設規模過大。在距離和容量雙重限制下得到配送中心最終解。

[關鍵詞]多配送中心 選址 距離限制 容量限制

一、引言及綜述

選址問題不僅直接關系到日后配送中心自身的運營成本和服務水平，而且配送中心選址問題屬于物流系統的長期規劃項目，建設地點一旦選定則很難改變。

郜振華提到影響物流選址的定性和定量因素，進而利用層次分析法進行選址。苗興東對重心法進行物流選址求得的最優解從數學原理上進行了分析。李強利綜合考慮產品的運輸費用、配送中心的可變成本和固定成本，對重心法進行改進。岳金輝提出雙層規劃和K-Harmonic means聚類分析相結合的的學校位置選擇研究。

二、帶距離和容量限制的選址問題描述

在一個大的配送區域內，為了減少持貨量，需在配送中心間進行調撥貨物。若距離太遠，調撥時就需要花費較多的運輸費用，另外，若無法及時從臨近的配送中心進行補貨，則會降低服務水平。因比在選址時需要對鄰近配送中心間進行距離限制，使其距離不超過給定的上限，這就是帶距離限制的配送中心選址問題。當配送中心的容量過大時，會增加建設成本。因此，建立配送中心時往往需要考慮容量限制。以此實現提高企業服務水平和降低配送成本兩大目標。

三、距離和容量雙重限制選址實證分析

（一）帶距離限制的選址模型

將n個需求點任意劃分m個區域，m=2，計算出每個區域的重心位置作為初始配送中心地點;計算每個需求點到所屬區域重心位置的距離。若某個需求點到所在區域重心的距離小于到其他區域重心的距離，那么該點屬于原所在區域，否則將該點調整到離它最近的重心點所在的區域;經過調整后，若配送中心間距離均不超過L，則停止計算。否則。m=m+1，重新開始。

（二）帶容量限制的選址模型

當A1區需求量超過容量限制時，就要將A1區需求點調整到其他的區域，以滿足A1區域不超過容量限制的約束。首先選擇離其他區域重心最近的需求點進行調整，將此需求點調整到相應的區域后，重新計算各個區域的重心位置及各區域的總需求量是否滿足容量限制，若滿足則停止計算，否則，繼續調整，直至所有區域均滿足容量限制為止。

（三）實證分析

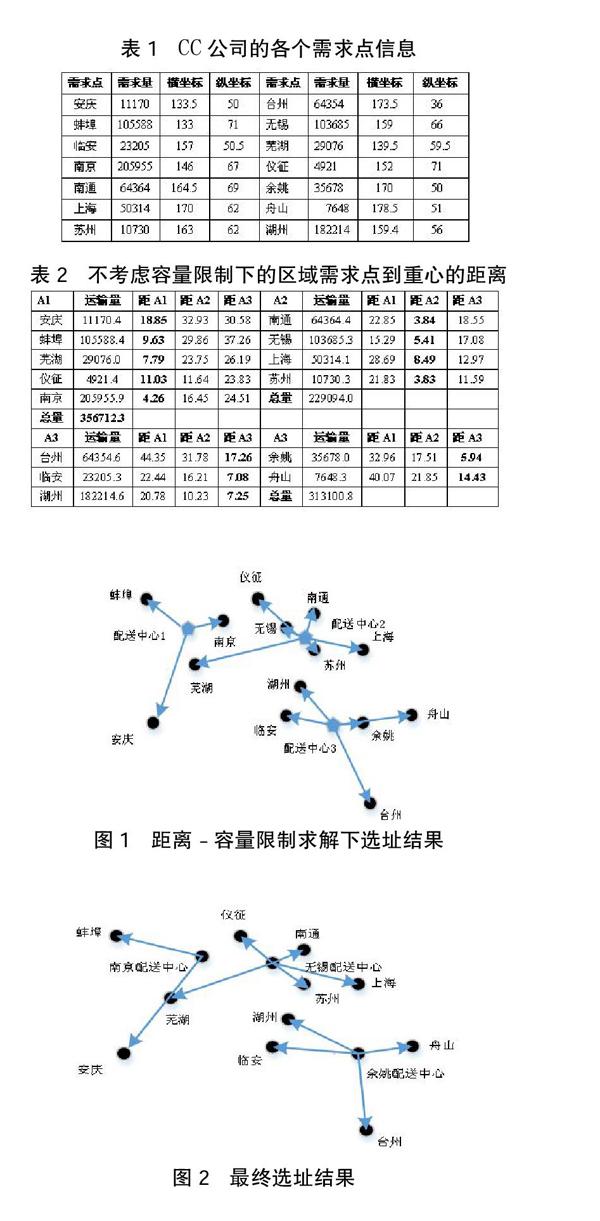
（1）運用帶距離限制模型初求解，首先設定在距離限制中各配送中心之間最大距離L=21以及在帶容量限制中配送中心容量Q=344000kg。表1列出cc公司的14個需求點的需貨量、城市距離系數及城市坐標等信息。

采用重心法計算中心位置。經模型計算，當m=2時，經過調整得到的兩個配送中心間的距離不滿足L設定要求。因此須增加配送中心數量。當m=3時，運用帶距離限制模型再次對各區域內的需求點進行調整。最終如表2所示：

（2）帶容量限制模型優化。為了減少調整次數，可采取預調試策略。當總需求量超過容量限制時，首先考慮的是該區域內離其他區域最近的可移動點，移動前，先判斷目標區域的總需求量是否超過容量限制，若超過，則尋找區域內離其他區域次近距離的需求點，并進行同樣的預調測試，直至找到滿足條件的需求點再進行移動調整。調整結果如圖1。

四、結論

重心法選址屬于連續型選址，所得出地點通常只是理論最佳位置，有時候無法運用到實際的選址規劃中，為了避免上述問題，更通常的做法是先利用連續性求得初始解，選擇靠近初始解的備選點作為最終選址結果以保證選址的質量。故最終三個配送中心分別為：南京、無錫、余姚。服務范圍如下圖2所示。